Моделирование топологии взаимодействия субъектов транспортного рынка посредством потоков различных типов

Куренков П.В.; Kurenkov P.V.

doi:10.36718/2500-1825-2020-2-79-92

Научные статьи \ Экономика. Народное хозяйство. Экономические науки \ Экономическое положение. Экономическая политика. Управление и планирование в экономике. Производство. Услуги. Цены \ Производство продукции и услуг по отраслям народного хозяйства

Моделирование топологии взаимодействия субъектов транспортного рынка посредством потоков различных типов

Автор: Куренков П.В.

Журнал: Социально-экономический и гуманитарный журнал Красноярского ГАУ @social-kgau

Рубрика: Экономика

Статья в выпуске: 2 (16), 2020 года.

Бесплатный доступ

В статье говорится о связи потоков различных типов (транспортных, грузовых, информационных, финансовых, энергетических, правовых и других) между собой и элементами в системе доставки внешнеторговых грузов (СДВТГ), приводится модель топологии их взаимодействия с определением интегрального показателя качества того или иного маршрута или варианта доставки. Мера сложности структуры СДВТГ может определяться не только для схем поставок, определения степени взаимодействия различных типов элементов и потоков, но и для субъектов, оказывающих информационные, таможенные, экспедиторские, сюрвейерские, складские, стивидорные и другие услуги. Предлагаемый алгоритм позволяет: во-первых, произвести оценку и анализ структуры СДВТГ одним интегральным показателем качества; во-вторых, определить степень интегрированности симплексов, дуплексов, мультиплексов, элементов, потоков, подсистем и отдельно взятых структур в общую структуру СДВТГ; в-третьих, сгруппировать отдельные категории симплексов, дуплексов, мультиплексов, элементов, потоков, подсистем, отдельно взятых структур, маршрутов или схем поставок в СДВТГ в зависимости от сложности или отдельных критериев и по ранжиру качества выбрать наиболее подходящие для пользователя транспортными услугами. В статье структура СДВТГ рассматривается как состоящая из 21 взаимодействующего комплекса (21 - прямые и 21 - обратные): комплексов элементов, комплексов потоков различных типов - транспортных, грузовых, информационных, финансовых, энергетических и комплексов правовых связей. Рассматривается коэволюционное взаимодействие под углом зрения его организации, где есть цепная связь конъюгирующих комплексов, для которой характерны асимметрия и наличие связи (инверсии по Богданову А.А.). При этом разрыв связи в коэволюционном взаимодействии влечет за собой или дезорганизацию, или появление отдельных независимых комплексов.

Еще

Элемент, поток, система, взаимодействие, доставка, вагон, груз, мультиплекс, комплекс

Короткий адрес: https://sciup.org/140249975

IDR: 140249975 | УДК: 338.47:656 | DOI: 10.36718/2500-1825-2020-2-79-92

Modeling the topology of interaction of transport market subjects by the flows of various types

In the study it is told about communication of streams of various types (transport, cargo, information, financial, power, legal and others) among themselves and elements in the system of delivery of the foreign trade cargoes (further - SDFTC), the model of topology of their interaction with definition of an integrated indicator of quality of any given route or option of delivery is given. The measure of complexity of structure of SDFTC can be defined not only for schemes of deliveries, definition of extent of interaction of various types of elements and streams, but also for the subjects rendering information, customs, forwarding, surveyor, warehouse, stevedoring and other services. The offered algorithm allows first, to make the assessment and the analysis of the structure of SDFTC one integrated indicator of quality, secondly, to define degree of integration of simplex, duplexes, multiplexes, elements, streams, subsystems and single structures in the general structure of SDFTC and, thirdly, to group separate categories of simplex, duplexes, multiplexes, elements, streams, subsystems, single structures, routes or schemes of deliveries to SDFTC depending on the complexity or separate criteria and on a formation of quality to choose the most suitable for the user transport services. In the study the structure of SDFTC is considered as consisting of 21 interacting complexes (21 straight lines and 21 returns): complexes of elements, complexes of streams of various types - transport, cargo, information, financial, power and complexes of legal communications. In the study typical coevolution interaction from this point of view of its organization where there is a chain communication of the conjugating complexes of which the asymmetry and the existence of communication (inversions according to A.A. Bogdanov) is considered. At the same time the rupture of the communication in coevolution interaction involves either disorganization, or emergence of separate independent complexes.

Еще

Текст научной статьи Моделирование топологии взаимодействия субъектов транспортного рынка посредством потоков различных типов

В работе [5, с. 66] отмечается, что оптимизация управления потоками создаст более благоприятные условия для ритмичной работы и согласования перевозок с другими видами транспорта, а правильно рассчитанный подвод грузов к портам и пограничным переходам даст возможность экономичного использования подвижного состава. Решение данной проблемы на новом уровне стало возможным в связи с повсеместным внедрением цифровых информационных технологий.

Впервые транспортные, грузовые, информационные, финансовые и энергетические потоки в едином комплексе были рассмотрены в работе О.В. Белого [2, с. 3, 5].

Функцию стыкования транспортных, грузовых, информационных и финансовых потоков с энергетическими выполняют энергодиспетчеры дирекций железных дорог, энергоучастков, электростанций, тяговых подстанций и т.д.

На основании вышеизложенного предлагается иерархическая схема пунктов взаимодействия различных типов потоков, включающая диспетчерские, информационные, ситуационные и другие центры управления грузовыми перевозками в системе смешанных сообщений (рис.).

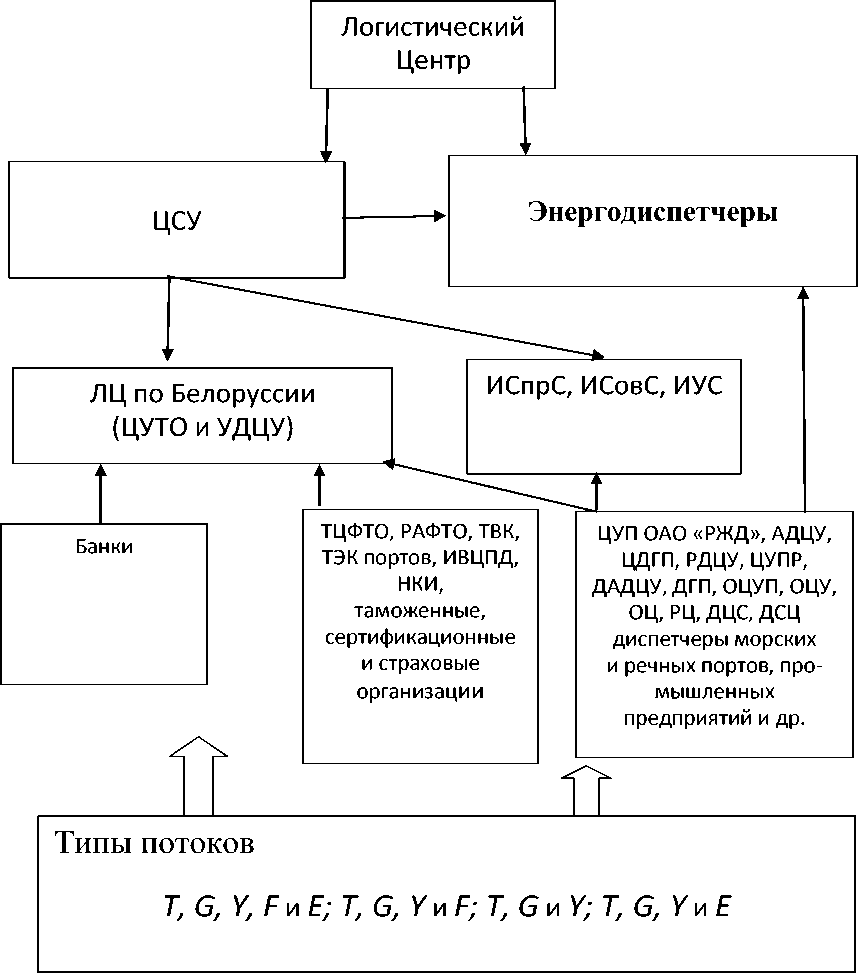
Иерархическая схема пунктов взаимодействия различных типов потоков

Представление структуры СДВТГ в виде совокупности мультиплициальных комплексов

Всю структуру системы доставки внешнеторговых грузов (СДВТГ) можно представить как совокупность элементов Х = {станция (порт)

погрузки, грузоотправитель, грузовладелец, железнодорожные перегоны, станции расформирования или формирования составов поездов, станция (порт) выгрузки, грузополучатель, экспедитор и т.д.) и совокупность потоков (транспортных – T , грузовых – G , информационных – Y , финансовых – F , энергетических – Е и правовых связей – P ), взаимодействующих между собой. В свою очередь, каждый элемент, поток и правовую связь можно категорировать – отнести к той или иной категории.

Каждому элементу или подсистеме СДВТГ должен быть поставлен в соответствие динамический массив, состоящий из постоянных и переменных параметров текущего, прогнозного и архивного состояний. Параметрами являются не только нормативно-справочная информация Правил перевозок грузов, Тарифных руководств и различных ГОСТов, но и функциональные свойства элементов, определяемые паспортами клиентов, техническо-распорядительными актами работы станций, планом формирования поездов, сводами обычаев морских торговых портов, уставами предприятий, лицензиями, сертификатами и т.д.

Каждый параметр, характеризующий элементы (производительность перегрузочного оборудования, складская емкость, длина перегона, наличие лицензий или права оказания различных видов услуг в области транспортного бизнеса, порядок обработки на станциях прибывающих и отправляемых составов поездов, порядок подачи/уборки вагонов в/из порта, право на оплату тарифа по Прейскуранту 10-01 и по ставкам Тарифной политики, банк, в котором находится расчетный счет субъекта РТУ, базисные условия внешнеторговых контрактов и т.д.), имеет свое функциональное назначение и оказывает влияние как на состояние и функционирование отдельно взятого элемента или подсистемы СДВТГ, так и на порядок взаимодействия элементов с потоками различных типов и категорий, потоков различных типов между собой, элементов и потоков с правовыми связями – то есть на состояние и функционирование СДВТГ в целом.

Другими словами, одно из важнейших (качественных) свойств СДВТГ заключено главным образом в силе связности ее элементов, транспортных, грузовых, информационных, финансовых и энергетических потоков при определенной технологии и правовой базе их взаимодействия или, другими словами, это есть то топологическое пространство состояния, в котором заключено качественное свойство СДВТГ. Оно представляет собой пространство, которое можно назвать пространством структуры элементов, структур всех типов потоков и структуры правовых связей различных категорий, так как именно структура взаимосвязи элементов, потоков и правовой базы или же отдельных подсистем СДВТГ определяющим образом влияет на ее функционирование. С изменением (исчезновением или ослаблением) связности между отдельными элементами (закрытие линий, стихийные бед- ствия, войны, межгосударственные конфликты, арест расчетного счета, расторжение договоров купли-продажи, договоров на экспедирование, фрахтование, декларирование, лишение лицензий, отключение электричества и т.д.) происходит либо исчезновение самой СДВТГ, либо изменение ее функциональных свойств (качества).

Информацию о качественном состоянии СДВТГ в статике может дать ее описание в терминах отношений инцидентности.

В общем случае насыщенный линейный план в к -мерном пространстве представляет собой совокупность из M+1 точек, размещенных в этом пространстве таким образом, что они не принадлежат одновременно никакому подпространству размерности меньше чем M. Такие точки задают вершины геометрической фигуры, которая называется к-мерным симплексом [4, 11, 13, 15]. Фигуры, составленные из симплексов (так называемые полиэдры), рассматривал еще А. Пуанкаре при построении теории гомологии - одного из разделов топологии [12,16].

Понятие «симплекс» формулируется следующим образом: симплекс - это выпуклая оболочка линейно независимых точек в евклидовом пространстве или гомеоморфный образ; указанные точки называются вершинами симплекса, а уменьшенное на единицу их число - размерностью симплекса . Всякое подмножество вершин симплекса также определяет симплекс - грань исходного симплекса. Правильное примыкание симплексов в полиэдре означает, что симплексы могут пересекаться только по их общей грани.

Однако, согласно компьютерной терминологии, существует и отличное понятие. В [14, с. 438] сказано, что «между вершинами симплекса данные могут перемещаться только в одном направлении и невозможно движение потока данных в противоположном направлении». При этом имеется в виду только информационный поток. В СДВТГ не только информационный, но и все остальные типы потоков перемещаются в обоих направлениях (обмен информацией, возврат неправильно начисленных денежных сумм, возвращение подвижного состава к своему владельцу, возврат груза на станцию отправления вследствие коммерческой неисправности и др.), поэтому данный термин для моделирования соответствующих процессов неприемлем. Термин « дуплекс (du-plex) », характеризующий возможность одновременной передачи данных (движения информационного потока) в обоих направлениях [14, с. 157], также является не совсем подходящим, поскольку между одними и теми же элементами СДВТГ и субъектами РТУ (ж.-д. станциями, портами, экспедиторами и т.д.) перемещаются потоки различных типов. Поэтому наиболее подходящим для формализации взаимодействий между элементами, потоками и правовыми связями в СДВТГ представляется термин « мультиплекс (multiplex) », характеризующий перемещение всех типов потоков в любых направлениях, их взаимодействие с элементами, правовыми связями и между собой [8-10].

M-мерный мультиплекс определяется своими M+1 вершинами t1, t2,™, ta,™, tl; g1, g2,™, gb,™, gz; y1, y2,™, yj,™, ym; fl , f2 ,™, fc ,™, fh; p1 , p2 ,™, pd,…, pv и т.д., которые являются точками общего положения. Это означает, что все они не лежат ни в одной из (M-1)-мерной гиперплоскости.

Для моделирования взаимодействия элементов х i , потоков t a , g b , у j , f c , e w и правовых связей p d (x ∈ X, t ∈ T , g ∈ G , y ∈ Y , f ∈ F , e ∈ E , p ∈ P) на произведениях Х и T, Х и G, Х и Y, Х и F, Х и E, Х и P , а также всех остальных введены отношения λ t^x ∈ X×T , λ g^x ∈ X×G , λ y^x ∈ X×Y , λ f^x ∈ X×F , λ e^x ∈ X×E , λ p^x ∈ X×P и т.д., которые существуют между множествами Х и T, Х и G, Х и Y, Х и F, Х и E, Х и P и т.д. тогда и только тогда, когда входящие в их состав элементы, потоки и правовые связи взаимодействуют между собой.

При этом под каждым мультиплексом подразумевается некое взаимодействие элементов, потоков различных типов и правовых связей между собой (например, «грузовая отправка ↔ судно», «транзитный вагон с переработкой ↔ сортировочная станция», «таможенные платежи ↔ банк», «штурманская расписка ↔ ТЭК», «документ, подтверждающий экспорт товара ↔ возврат НДС», «договор на оказание информационных услуг ↔ дислокация вагона или груза» , «энергетический поток ↔ железнодорожный перегон» , «комплект перевозочных документов ↔ товарная контора» , «заявка на грузовую перевозку ↔ ДЦФТО» и т.д.), а совокупность таких мультиплексов составляет структуру всей СДВТГ.

В таблице 1 приведены обозначения отношений и матриц инцидентности, а также мультиплициальных комплексов для соответствующих произведений структур элементов, потоков и правовых связей.

Таблица 1

Обозначения мультиплициальных комплексов, отношений и матриц инцидентности для соответствующих прямых произведений структур элементов, потоков различных типов и правовых связей

Прямые произведения	Отношения инцидентности	Матрицы инциденций	Мультиплициальные комплексы
1	2	3	4
Х и T	λ tx ∈ X×T	Λ t^x =(λ ia )	M x^t (T;λ t^x )
Х и G	λ g x ∈ X×G	Λ g ^x =(λ ib )	M x ^g (G;λ g ^x )
Х и Y	λ yx ∈ X×Y	Λ y^x =(λ ij )	M x^y (Y;λ y^x )
Х и F	λ fx ∈ X×F	Λ f^x =(λ ic )	M x^f (F;λ f^x )
T и G	λ g t ∈ T×G	Λ g^t =(λ ab )	M t ^g (G;λ g ^t )
T и Y	λ yt ∈ T×Y	Λ y^t =(λ aj )	M t^y (Y;λ y^t )
T и F	λ ft ∈ T×F	Λ f^t =(λ ac )	M t^f (F;λ f^t )
G и Y	λ y g ∈ G×Y	Λ y ^g =(λ bj )	M g^y (Y;λ y ^g )
G и F	λ f g ∈ G×F	Λ f ^g =(λ bc )	M g ^f (F;λ f ^g )

Окончание табл. 1

1	2	3	4
Y и F	λ fy ∈ Y×F	Λ f^y =(λ jc )	M y^f (F;λ f^y )
E и X	λ ie ∈ E×X	Λ x^e =(λ wi )	M e^x (X;λ x^e )
E и T	λ te ∈ E×T	Λ t^e =(λ wa )	M e^t (T;λ t^e )
E и G	λ g e ∈ E×G	Λ g^e =(λ wb )	M e ^g (G;λ g ^e )
E и Y	λ ye ∈ E×Y	Λ y^e =(λ wj )	M e^y (Y;λ y^e )
E и F	λ fe ∈ E×F	Λ f^e =(λ wc )	M e^f (F;λ f^e )
E и P	λ fp ∈ E×P	Λ f^p =(λ wd )	M e^p (P;λ f^e )
P и X	λ ip ∈ P×X	Λ x^p =(λ di )	M p^x (X;λ x^p )
P и T	λ tp ∈ P×T	Λ t^p =(λ da )	M p^t (T;λ t^p )
P и G	λ g p ∈ P×G	Λ g ^p =(λ db )	M p ^g (G;λ g ^p )
P и Y	λ yp ∈ P×Y	Λ y^p =(λ dj )	M p^y (Y;λ y^p )
P и F	λ fp ∈ P×F	Λ f^p =(λ dc )	M p^f (F;λ f^p )

Таким образом, структура СДВТГ рассматривается как состоящая из 21 взаимодействующего комплекса (21 – прямые и 21 – обратные): комплексов элементов , комплексов потоков различных типов – транспортных, грузовых, информационных, финансовых, энергетических и комплексов правовых связей.

Коэволюционное взаимодействие, рассмотренное под углом зрения его организации, есть цепная связь конъюгирующих комплексов, для которой характерны асимметрия и наличие связи (инверсии по А.А. Богданову) [6, с. 17]. Разрыв связи в коэволюционном взаимодействии влечет за собой или дезорганизацию, или появление отдельных независимых комплексов. Эти идеи, выдвинутые А.А. Богдановым в начале ХХ века, относятся к исследованию формирующих организационных механизмов или механизмов формирования организационного взаимодействия (в нашем случае, если следовать Образцову В.Н., Звонкову В.В., Комарову А.В., Милославской С.В., Персианову В.А. и др., – теории комплексной эксплуатации разных видов транспорта, совмещенной технологии грузовых перевозок в смешанном сообщении, системному анализу структуры и технологии функционирования транспортных узлов) и не касаются механизмов изменения организационных структур или организационных форм управления системой доставки внешнеторговых грузов (СДВТГ).

Для оценки качественного (топологического) свойства структуры СДВТГ введен показатель – «мера сложности» структуры – Ψ СДВТГ (M). Меры сложности взаимодействия структур элементов – Ψ x (M), потоков различных типов Ψ t (M), Ψ g (M), Ψ y (M), Ψ f (M), Ψ e (M) и правовых связей Ψ p (M) определяются через координаты соответствующих векторов Q ^x , Q ^t , Q ^g , Q ^y , Q ^f , Q ^e и Q ^p по формулам, приведенным в таблице 2.

Таблица 2

Определение меры сложности взаимодействия структур элементов, потоков и правовых связей в СДВТГ

Мера сложности структур элементов, потоков и правовых связей при их влиянии друг на друга	Мера сложности взаимодействия структур
1	2
^ xt (M xt ) = 2{Z (i+1) * Q i ^xt }/ [ (N xt +1)(N xt +2) ]	T tx (M)= VT xt (M)²+ T tX (M) 2
T x (M tx ) = 2{Z (a+1) * Q at } / [ (N tx +1)(N tx +2) ]
T x g M x ) = 2{Z (i+1) * Q ix g } / [ (N ^ g +1)(N x g +2) ]	T gx (M)= VT e g (M)²+ T g x (M> 2
TKM g ) = 2{Z (b+1) * Q b g x }/ [ (N g ^X+1)(N g x +2) ]
У хУ (М хУ ) = 2{Z (i+1) * Q X } / [ (N y +1)(N xy +2) ]	T yx (M)= VT xy (M)²+ T yX (My 2
T yx (M yx ) = 2{Z (j+1) * Q y }/ [ (N yx +1)(N yx +2) ]
Yf(Mf) = 2{Z (c+1) * Q f } / [ (Nf+1)(Nf+2) ]	T fx (M)= VT xf (M)²+ Yf (M)²
T/(M/) = 2{Z (i+1) * Q iXf }/ [ (W+1)(N xf +2) ]
TKM g ) = 2{Z (b+1) * Q b g t }/ [ (N g t +1)(N g t +2) ]	T g t (M)= VT g t (M)²+ T g (M)
T g M t g ) = 2 {Z (a+1) * Q at g } / [ (N t g +1)(N g +2) ]
T yMj M y ) = 2{Z (j+1)*Q jyt }/ [ (N yt +1)(N yt +2) ]	T ty (M)= VT yt (M)²+ T y (M) 2
W(M#0 = 2{Z (a+1) * Q aty }/ [ (N ty +1)(№+2) ]
Vf(Mf) = 2{Z (c+1) * Q g }/ [ (N f +1)(N f +2) ]	T ft (M)= VT jt (M) 2 + T tf (M) 2
T f (M f ) = 2{Z (a+1) * Q atf }/ [ (N tf +1)(N tf +2) ]
T yg (M y g ) = 2{Z (j+1) * Q j ^y ^g } / [ (N y g +1)(N y g +2) ]	T g y (M)= VT y g (M) 2 + T g y (M) 2
T g y (M g y ) = 2 {Z (b+1) * Q g }/ [ (N g y +1)(N g y +2) ]
T g M g ) = 2{Z (c+1) * Q f } / [ (N ^g +1)(N f + 2) ]	T g f (M)= VT j g (M)²+ Т/(М) 2
T (M f = 2 {Z (b+1) * Q bf }/ [ (N/+1)(N g +2) ]
T y (M fy ) = 2{Z (j+1) * Q jfy }/ [ (N fy +1)(N fy +2) ]	T yf (M)= VT fy (M)²+ T y ^f(M) 2
T f (M yf ) = 2{Z (c+1) * Q cyf } / [ (N yf +1)(N yf +2) ]
T ex (M ex ) = 2{Z (w+1) * Q wex }/ [ (N e ^x+1)(N e ^x+2) ]	T xe (M)= VT eX (M)²+ T xe (M)²
^ xe (M xe ) = 2 {Z (i+1) * Q ixe }/ [ (N x ^e+1)(N x ^e+2) ]
Т еЧМ е¹ ) = 2{Z (W+1) * Q wet }/ [ (N et +1)(N et +2) ]	T te (M)= VT et (M)²+ T te (M)²
^ te (M te ) = 2{Z (a+1) * Q ate }/ [ (N t ^e+1)(N t ^e+2) ]
T eS (M e g ) = 2{Z (W+1) * Q we g } / [ (N e g +1)(N e g +2) ]
	T g e (M)= VT e g (M)²+ T g e (M)²
V g4 M g^e ) = 2{Z (b+1) * Q b g e }/ [ (N g ^e+1)(N g e +2) ]
Т еУ СМ еУ ) = 2{Z (W+1) * Q wey }/ [ (N ey +1)(N ey +2) ]	T ye (M)= VT ey (M)²+ T y ^e(M)²
T y ^e(M y ^e) = 2{Z (j+1) * Q jye }/ [ (N y ^e+1)(N y ^e+2) ]
T fe (M fe ) = 2{Z (c+1) * Q cfe }/ [ (Nf+1)(Nf+2) ]	T fe (M)= VT ef (M) 2 + Tf(M) 2
T ef (M ef ) = 2{Z (W+1) * Q wef }/ [ (N ef +1)(N+) ]
T pe (M pe ) = 2{Z (d+1) * Q dPe }/ [ (N pe +1)(N pe +2) ]	T Pe (M)= VT eP (M)²+ T>e (M)²
T eP (M eP ) = 2{Z (w+1) * Q weP }/ [ (N eP +1)(N eP +2) ]
T pX (M pX ) = 2{Z (d+1) * Q dPx }/ [ (N pX +1)(N pX +2) ]	T xp (M)= VT pX (M)²+ T xP (M)²
T xP (M xP ) = 2{Z (i+1) * Q ixP }/ [ (N xP +1)(N xP +2) ]
T pt (M pt ) = 2{Z (d+1) * Q dPt }/ [ (N Pt +1)(N Pt +2) ]	T tP (M)= VT Pt (M)²+ T P (M) 2
T tP (M tP ) = 2{Z (a+1) * Q atP }/ [ (N tP +1)(N tP +2) ]
T) g (M P g ) = 2{Z (d+1) * Q dP g }/ [ (N Pg +1)(N Pg +2) ]	T g P (M)= VT P g (M) 2 + T g^ (M) 2
T g ? CM g ? ) = 2{Z (b+1) * Q b g P }/ [ (Ng=+1)(N g P +2) ]

Окончание табл. 2

1 2 Tpy(Mpy) = 2{Z(d+1)*Qdpy}/ [(Npy+1)(Npy+2)] Typ(M)= VTpy(M)2+ Typ(M)2 Typ(Myp) = 2{Z(j+1)*Qjyp}/ [(Nyp+1)(Nyp+2)] Tfp(Mfp) = 2{E(c+1)*Qcfp}/ [(Nfp+1)(Nfp+2)] Tfp(M)= VTpfCM)2+ Tfp(M)2 Tpf(Mpf) = 2{Z(d+1)*Qdpf}/ [(Npf+1)(Npf+2)] где Nx, Nt, Ng, Ny, Nf, Ne, Np и т.д. - размерности мультиплициальных комплексов Mx, Mt, Mg, My, Mf, Me, Mp и т.д., равные наибольшим значениям qtx, qgx, qyx, qfx, qex и qpx (Nt=dim Mt, Ng=dim Mg, Ny=dim My, Nf =dim Mf, Ne =dim Me и Np=dim Mp);

Q i^x , Q at , Q b g , Q j^y , Q cf , Q we и Q dp , - соответственно i -я, a -я, b -я, j -я, c -я, w -я и d -я компоненты, векторов Q x , Q t , Q ^g , Q ^y , Q f , Q e и Q p , получаемые в результате q -анализа.

Таким образом, получаем разные векторы для структуры элементов Q ^x , для структур потоков Q ^t , Q ^g , Q ^y , Q ^f , Q ^e и для структуры правовых связей Q ^p . Вычисляя меры сложности расположения в системе элементов T x (M), потоков T t (M), T^M), T y (M), T f M), T e (M) и правовых связей T p (M) с учетом их взаимодействия , могут быть получены количественные характеристики качества структуры СДВТГ.

Длина вектора Т сдвтг (М) от начала координат, который является полным вектором структуры СДВТГ, равна

Т сдвтг = v^ tx² + T g ² + T yx² + T fx² + ^F g t² + T ty² + T f² + T g y² + T f + T yf +

____________________z_____:_____:______:______:____:_____-______________ (1) + T xe² + T te² + T g e² + T ye² + T fe² + T pe² + T xp² + T tp² + T g p² + T yp² + T fp²

Несмотря на то что q- анализ является довольно эффективным подходом при изучении степени связности СДВТГ, тем не менее он не дает необходимой информации, насколько важен (интегрирован) каждый мультиплекс в общей структуре СДВТГ. Для учета индивидуальных свойств мультиплексов необходимо знать численное значение степени интегрированности каждого отдельного мультиплекса в структуре всей СДВТГ. Относительная важность того или иного элемента, потока и правовой связи в общей структуре СДВТГ характеризуется их эксцентриситетами.

В связи с этим вводятся следующие обозначения:

g - верхнее значение q для x i или t a , g b , y j , f c , e w и p d , т.е. q = dim M ;

g - нижнее значение q для X i или t a , g b , y j , f c , e w , и p d .

То есть q равно наибольшему значению q , при котором X i , t a , g b , y j , f c , e w и p d имеет связность с каким-либо другим мультиплексом, соответственно из комплексов M xt (T;^ tx ) и M t^X (X;A tx-1 ), M x g (G;X g x ) и M g x (X;X g x-1 ), M xf (F;X fx ) и M jX (X;X fx-1 ), M xe (E;X ex ) и M eX (X;X ex-1 ), M xp (P;X px ) и M pX (X;X px-1 ), а также всех остальных.

Тогда эксцентриситеты отдельно взятых мультиплексов определяются следующим образом:

Ecc(x i ,t a ) = ( g - g )/( g +1) ;

Ecc(x i , g b ) = ( g - g )/( g +1) ;

Ecc(x i ,y j ) = ( g - g )/( g +1) ; (2 )

Ecc(x i f c ) = ( g - g )/( g +1) ;

Ecc(x i ,e w ) = ( g - g )/( g +1) ;

Ecc(x i ,p d ) = ( g - g )/( g +1) и т.д.

Разность g - g является мерой необычности любого мультиплекса а. При этом равенство g - g =2 считается более значимым, если q=1 , а не когда q=10 . Поэтому в качестве значимости эксцентриситетов будем использовать вышеприведенные отношения (2), а не абсолютную разность g - g . Значения эксцентриситетов различных мультиплексов позволяют оценить, насколько каждый элемент, поток или правовая связь интегрированы в общую структуру СДВТГ, то есть их значимость в ее функционировании.

В таблице 3 приведены обозначения структурных векторов, частотных матриц отношений, матричного анализа мультиплициальных комплексов и эксцентриситетов мультиплексов в этих комплексах.

Таблица 3

Структурные вектора, частотные матрицы отношений и эксцентриситеты мультиплексов в мультиприциальных комплексах

Структурные вектора	Частотные матрицы отношений	Матричный анализ комплексов	Эксцентриситеты мультиплексов
1	2	3	4
Q tx	Ω х^t ( ∀ i,a)(ω ia =ω ai )	Λ tx Λ tx^T - Ω x^t	Есс(х i ,t a )
Q g x	Ω х ^g ( ∀ i,b)(ω ib =ω bi )	Λ g x Λ gx^T - Ω x g	Есс(х i , g b )
Q yx	Ω х^y ( ∀ i,j)(ω ij =ω ji )	Λ yx Λ yx^T - Ω x^y	Есс(х i ,y j )
Q fx	Ω х^f ( ∀ i,c)(ω ic =ω ci )	Λ fx Λ fx^T - Ω x^f	Есс(х i ,f c )
Q g t	Ω t ^g ( ∀ a,b)(ω ab =ω ba )	Λ t g Λ t g ^T - Ω t ^g	Есс(t a , g b )
Q yt	Ω t^y ( ∀ a,j)(ω aj =ω ja )	Λ ty Λ ty^T - Ω t^y	Есс(t a ,y j )
Q ft	Ω t^f ( ∀ a,c)(ω ac =ω ca )	Λ tf Λ tf^T - Ω t^f	Есс(t a ,f c )
Q y g	Ω g ^y ( ∀ b,j)(ω bj =ω jb )	Λ g y Λ g y^T - Ω g ^y	Есс( g b ,y j )
Q f g	Ω g ^f ( ∀ b,c)(ω bc =ω cb )	Λ g f Λ g f^T - Ω g ^f	Есс( g b ,f c )
Q yf	Ω f^y ( ∀ c,j)(ω cj =ω jc )	Λ fy Λ fy^T - Ω f^y	Есс(f c ,y j )
Q xe	Ω e^x ( ∀ w,i)(ω wi =ω iw )	Λ xe Λ xe^T - Ω e^x	Есс(e w ,x i )

Окончание табл. 3

1	2	3	4
Q te	Ω e^t ( ∀ w,a)(ω wa = ω aw )	Λ te Λ te^T - Ω e^t	Есс(e w ,t a )
Q g e	Ω e ^g ( ∀ w,b)(ω wb =ω bw )	Λ ge Λ ge^T - Ω e g	Есс(e w , g b )
Q ye	Ω e^y ( ∀ w,j)(ω wj =ω jw )	Λ ye Λ ye^T - Ω e^y	Есс(e w ,y j )
Q fe	Ω e^f ( ∀ w,c)(ω wc = ω cw )	Λ fe Λ fe^T - Ω e^f	Есс(e w ,f c )
Q pe	Ω e^p ( ∀ w,d)(ω wd =ω dw )	Λ pe Λ pe^T - Ω e^p	Есс(e w ,p d )
Q xp	Ω p^x ( ∀ d,i)(ω di =ω id )	Λ xp Λ xp^T - Ω p^x	Есс(p d ,x i )
Q tp	Ω p^t ( ∀ d,a)(ω da =ω ad )	Λ tp Λ tp^T - Ω p^t	Есс(p d ,t a )
Q g p	Ω p ^g ( ∀ d,b)(ω db =ω bd )	Λ gp Λ gp^T - Ω p ^g	Есс(p d , g b )
Q yp	Ω p^y ( ∀ d,j)(ω dj =ω jd )	Λ yp Λ yp^T - Ω p^y	Есс(p d ,y j )
Q fp	Ω p^f ( ∀ d,c)(ω dc =ω cd )	Λ fp Λ fp^T - Ω p^f	Есс(p d ,f c )

Выбор схемы поставки внешнеторгового груза

В качестве примера можно рассмотреть различные варианты маршрутов экспортно-импортных перевозок через морские порты и через сухопутные пограничные переходы. При этом могут иметь место варианты схем взаимного расположения звеньев в цепи транспортировки через морские (речные) порты России, СНГ и Балтии.

Алгоритм состоит в следующем. Составляются матрицы инциденций (взаимодействий) Λ между элементами, потоками и правовыми связями, описывающие структуру СДВТГ, транспонированные матрицы инциденций Λ ^T – для изучения обратного влияния взаимодействующих элементов, потоков и правовых связей друг на друга, матрицы ΛΛ ^T – Ω для анализа структур элементов, потоков и правовых связей, производится q -анализ комбинациями номеров строк и столбцов матриц Ω и q- анализ матриц ΛΛ ^T – Ω .

Целые числа на диагоналях пространственных матриц Ω являются размерностями мультиплексов. Наибóльшие по величине числа показывают размерности комплексов M .

Используя результаты анализа, полученные в ходе исследования различных вариантов доставки грузов через различные порты СНГ, России и Балтии, выбирается рациональный, оценив на сложность структуру СДВТГ для каждого из них.

Количество элементов, потоков и правовых связей множеств Х, T, G, Y , F, E и P может быть различным для каждого из исследуемых вариантов (маршрутов или схем) доставки.

Для оценки качества структуры СДВТГ, а в частном случае – для выбора схемы поставки внешнеторговых грузов – количество принимаемых во внимание факторов полностью зависит от требований заказчика на данную услугу и может быть любым – вплоть до простейшего варианта, когда во внимание принимается только общая стоимость доставки, включающая железнодорожный тариф, морской фрахт и различные сборы в пунктах отправления, назначения и перевалки с одного вида транспорта на другой.

Мера сложности структуры СДВТГ может определяться не только для схем поставок, определения степени взаимодействия различных типов элементов и потоков, но и для субъектов, оказывающих информационные, таможенные, экспедиторские, сюрвейерские, складские, стивидорные и другие услуги.

Ранжирование элементов, транспортных, грузовых, информационных, финансовых, энергетических и правовых потоков по категориям может выполняться как исходя из существующих разработок ученых и практиков, так и в зависимости от мнения субъекта, по заказу которого данные расчеты производятся. При отсутствии необходимости ранжирование может вообще не производиться. Аналогичным образом может осуществляться дифференцирование перевозчиков, экспедиторов, декларантов и других субъектов, получивших лицензии на различные виды деятельности (оказание различных услуг) в области транспортного бизнеса – собственным уставам, выданным установленным порядком в ОАО «РЖД» или в Минтрансе РФ сертификатам или же в зависимости от мнения самих грузовладельцев.

Предлагаемый алгоритм позволяет: во-первых, произвести оценку и анализ структуры СДВТГ одним интегральным показателем качества, во-вторых, определить степень интегрированности симплексов, дуплексов, мультиплексов, элементов, потоков, подсистем и отдельно взятых структур в общую структуру СДВТГ; в-третьих, сгруппировать отдельные категории симплексов, дуплексов, мультиплексов, элементов, потоков, подсистем, отдельно взятых структур, маршрутов или схем поставок в СДВТГ в зависимости от сложности или отдельных критериев и по ранжиру качества выбрать наиболее подходящие для пользователя транспортными услугами.

С. 40–43.

Список литературы Моделирование топологии взаимодействия субъектов транспортного рынка посредством потоков различных типов

Александров П.С. Комбинаторная топология. М.; Л.: Гостехиздат 1947. 660 с.
Белый О.В. Стратегия развития транспортной отрасли в условиях системного кризиса страны // Бюллетень транспортной информации. 1999. № 7-8. С. 2-6.
Борисович Ю.Г., Близняков Н.М., Израилевич Я.А. [и др.]. Введение в топологию. М.: Наука, 1995. 416 с.
Введение в топологию / Ю.Г. Борисович, Н.М. Близняков, Я.А. Израилевич [и др.]. М.: Наука, 1995. 416 с.
Воронин В.С. Информационное обеспечение перевозок // Железнодорожный транспорт. 2001. № 6. С. 65-66.
Жардемов Б.Б. Формирование и развитие структур железнодорожных станций и узлов (методы исследования и оценки). М.: МИИТ, 1999. 150 с.
Касти Дж. Большие системы. Связность, сложность и катастрофы. М.: Мир, 1982. 216 с.
Куренков П.В., Калушин А.А. Логистический подход к выбору схемы поставки товаров // Железнодорожный транспорт. 2000. № 11. С. 40-43.
Куренков П.В., Котляренко А.Ф. Внешнеторговые перевозки в смешанном сообщении: экономика, логистика, управление. Самара: Типография "Солдат Отечества", 2002. 636 с.
Куренков П.В., Фролов И.С. Моделирование экспорта угля через морские порты // Транспорт: наука, техника, управление: сб. ОИ / ВИ- НИТИ. 2001. № 7. С. 34-37.
Понтрягин Л.С. Основы комбинаторной топологии. М.: Наука, 1976. 136 с
Свитцер P.M. Алгебраическая топология. Гомотопии и гомологии. М.: Наука, 1985. 608 с
Спеньер Э. Алгебраическая топология. М.: Мир, 1971. 680 с
Толковый словарь по вычислительным системам / под ред. В. Иллингуорта и др.; пер. с англ. А.К. Белоцкого и др.; под ред. Е.К. Масловского. М.: Машиностроение, 1990. 560 с.
Фоменко А.Т. Наглядная геометрия и топология: математические образы в реальном мире. М.: Изд-во МГУ "ЧеРо", 1998. 416 с.
Хилтон П., Уайли С. Теория гомологий. М.: Мир, 1966. 452 с
Эткин Р.Х. Городская структура // Математическое моделирование. М.: Мир, 1989. С. 235-247.

Еще