Моделирование трафика открытой информационной системы с трансляцией GUI в потоковом видео

На сегодняшний день ведутся многочисленные дискуссии относительно построения систем облачных вычислений и в частности обсуждаются вопросы передачи GUI в потоковом видео. Исследования по этому вопросу находятся на начальном этапе развития, что следует из [1-2] и других публикаций.

Для получения количественных и качественных параметров функционирования системы предла- гается использовать структурно-имитационное моделирование. Проведение испытаний на реальных сетях не представляется возможным, так как существующие реализации обладают множеством ограничений [2-3]. Использование аналитического моделирования затруднено в связи с высокой сложностью объекта исследования. Одной из задач, возникающих при моделировании системы, является задача моделирования трафика, порождаемого при передаче GUI в потоковом видео. В общем случае в потоковом видео переносятся произвольные данные, которые характеризуются той или иной степенью сжатия. При передаче экранных форм в большинстве случаев требуется передавать изменения, происходящие на 0.5 – 5,0% области (анимация нажатия кнопок, скроллинг списков и т.д.). В некоторых случаях требуется передавать более развитую анимацию (например GUI графического редактора). Существует программное обеспечение, которое может включать анимацию разной степени интенсивности, например различные виды САПР.

Постановка задачи

При моделировании информационных систем с поддержкой передачи GUI в потовом видео возникает проблема описания трафика, формируемого при трансляции графического интерфейса пользователя. В [4-5] показано, что сетевой трафик, как правило, обладает свойствами самоподобия (self-similar) [6-7]. Для определения степени самоподобия в основном используют параметр Херста (Hurst). Физическая сущность данного критерия сводится к способности масштабирования статистических характеристик трафика как случайного процесса, что при решении практических задач верификации данных моделирования представляется весьма значимым и полезным при анализе задач проектирования вычислительных сетей.

В работах [8-10] описаны теоретические модели трафика, формирующегося в сетях разного типа, применение которых в имитационном эксперименте целесообразно с учетом ряда ограничений: таких как определенные законы поступления и обслуживания сетевых пакетов, количество и топология сетевых компонент и т.д. С другой стороны, использование эмпирических моделей на основе данных реального объекта позволит проводить исследования произвольных вычислительных сетей.

Настоящая статья посвящена задачам обоснования требований и структуры, а также организации экспериментальной системы и анализа экспериментальных данных передачи графического пользовательского интерфейса в потоковом видео, сбора сведений о сетевых пакетах и построения эмпирических моделей.

Решение задачи

Для проведения исследований была разработана система, включающая серверную и клиентскую части. На сервере функционирует программный медиасервер, осуществляющий трансляцию GUI, передаваемого посредством виртуальной камеры в режиме реального времени. Взаимодействие пользователя с приложением происходит на сервере. Там же реализован модуль формирования кадров и кодирование их в формате flv. Видеопоток GUI передается на клиентскую машину и отображается в браузере. Кроме того, на клиенте установлена система Wireshark, осуществляющая сбор и регистрацию входящих пакетов, а также их фильтрацию. Дополнительно разработан модуль формирования файла с хронометражем прихода сетевых пакетов для последующей передачи в системы обработки результатов замеров. Были протестированы 3 приложения: стандартный калькулятор, блокнот и Paint.NET. В рамках экспериментального сеанса взаимодействия с программами решались задачи по выполнению простых расчетов, набора текста, с сохранением в файл, редактирование фотографии.

Для анализа и сбора информации о сетевом трафике использована программа-сниффер «WireShark». Для установления свойств самоподобия изучаемого сетевого трафика необходимо фиксировать моменты прихода каждого пакета, а также интервалы между приходами соседних пакетов. Это требуется для определения статистических характеристик трафика, а также для усреднения по произвольным непересекающимся интервалам времени. Исходя из этих соображений, регистрировались следующие сведения о пакетах:

• -    «frame.time_delta» – время прихода пакета относительно данного пакета и предыдущего пакета;

• -    «frame.time_delta_displayed» – время прихода пакета относительно времени отправки данного пакета (записи);

• -    «frame.time_relative» – время прихода пакета относительно текущего и первого пакета;

• -    «num» – размер пакета (в байтах).

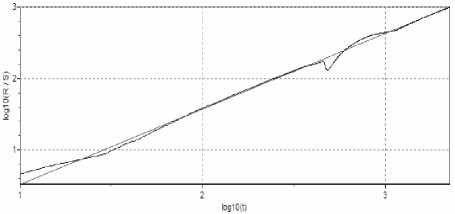
Рис. 1. График данных test _ time _ relative для сеанса взаимодействия с MS Calculator (H = 1,0599±0,0788)

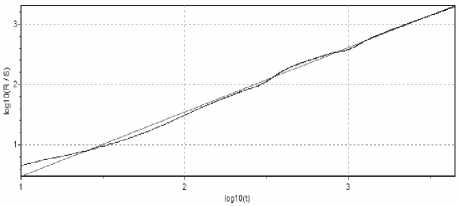
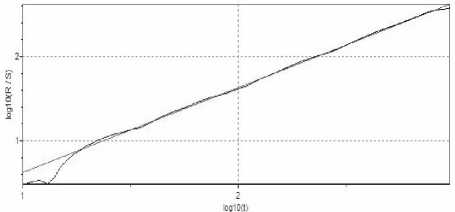
Рис. 3. График данных test_time_relative для сеанса взаимодействия с блокнотом (H = 1,0083±0,0468)

Для проверки определения параметра Херста использовалась программа Fractan 4.4. Для видеотрафика каждого сеанса работы с приложениями был вычислен показатель Херста. Для всех сеансов взаимодействия с приложениями построены графики данных test_time_relative, отражающие зависимость R/S от периода времени усреднения статистических характеристик (см. рис 1-3, где R – размах отклонения, а S – стандартное отклонение. Графики выполнены в логарифмическом масштабе, показатель Херста H определяется величиной наклона полученной прямой. Из графиков рис. 1-3 видно, что коэффициент Херста H > 0,7; что указывает на высокую длительную зависимость в процессе или самоподобие для всех сеансов взаимодействия с приложениями через транслируемый в потоковом видео графический интерфейс пользователя.

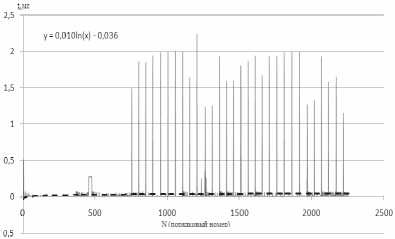
Рис. 5. Логарифмическая линия тренда для описания трафика сеанса с MS Calculator

Для получения эмпирической модели поступления сетевых пакетов был применен метод нахождения линии тренда на основе известного метода наименьших квадратов, где под трендом понимается долговременная тенденция изменения исследуемого временного ряда. Тренды могут быть описаны линейными, логарифмическими, степенными и т.д. уравнениями. Для поиска уравнения линии тренда была использована программа Microsoft Excel. В работе приводятся эмпирические модели на основе полиномиальной и логарифмической линий тренда, так как на основании приведенных ниже оценок стандартного отклонения можно сделать вывод о том, что они адекватны реальной системе.

Для сеанса взаимодействия с MS Calculator полиномиальная и логарифмическая линии тренда имеют вид:

у = 2Е - 08х² + 6Е - 05х - 0,004;      (1)

у = 0,0101 ln(x)-0,0361.              (2)

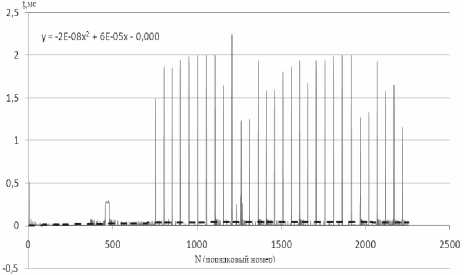
Рис. 4. Полиномиальная линия тренда для описания трафика сеанса с MS Calculator

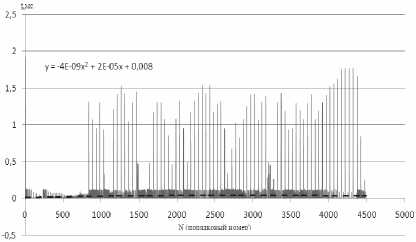
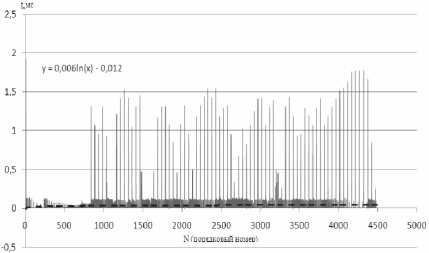
у = -4Е - 09х² + IE — 05х + 0,0086;     (3)

у = 0,0621п(х)-0,0128.

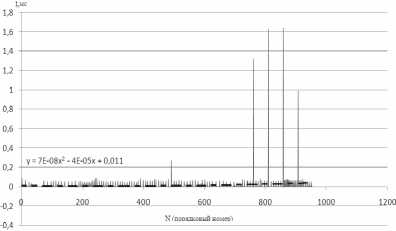
Рис. 8. Полиномиальная линия тренда для описания трафика сеанса с блокнотом

Рис. 9. Логарифмическая линия тренда для описания трафика сеанса с блокнотом

Для сеанса взаимодействия с блокнотом полиномиальная и логарифмическая линии тренда имеют вид:

у = 7Е-08х2 - 4Е - 05х + 0,0117; (5)

у = 0,00621п(х)- 0,0202. (6)

Определим линию тренда, которая лучше описывает зарегистрированный трафик. Для этого была разработана следующая GPSS модель, в которой интервал между приходом соседних пакетов задается линией тренда num VARIABLE {кол-во пакетов + 1};

GENERATE {уравнение линии тренда}, {отклонение от линии тренда}

QUEUE   PC ;Создание очереди к ПК

SEIZE    PC ;Захват пакета ПК

DEPART PC;

Уменьшение очереди на 1 пакет

ADVANCE 1 ;обработка пакета ПК

SAVEVALUE {сохраняемая ячейка}, (AC1/10000);

Запись времени пребывания пакета

RELEASE PC;

Освобождение ПК от захваченного пакета

TERMINATE1;

Счетчик обработанных пакетов

START{кол-во пакетов};

Запуск модели.

За единицу модельного времени выбрано значение 10-4 С. За отклонение было выбрано число, равное половине произведения значения линии тренда на текущем шаге на значение RN2/1000, где RN2 – случайное число от 0 до 999. Ниже приводятся фрагменты GPSS моделей для всех сеансов работы с приложениями.

• 1.    Сеанс работы с MS Calculator.

Число пакетов 2258 шт. Действительное время 72,5 С. Уравнения линии тренда:

• -    полиномиальная линия тренда со степенью 2:

GENERATE(ABS(-0.0002#(V$num-TG1)#(V$num-TG1) + 0.6#(V$num-TG1)-4)),

(RN2#ABS(-0.0002#(V$num-TG1)#(V$num-TG1) + 0.6#(V$num-TG1)-4)/2000)

Конечное время моделирования: 74,7 С. Отклонение от действительного времени: –2,6 С;

• -    логарифмическая линия тренда:

• 2.    Сеанс работы с Paint.NET

  Число пакетов 4490 шт. Действительное время 149,8 С. Уравнения линии тренда:

GENERATE (ABS(62#LOG(V$num-TG1)-202)),(RN2#ABS(62#LOG(V$num-TG1)-202) /2000).

Конечное время моделирования: 72 С. Отклонение от действительного времени: 0,5 С.

• -    полиномиальная линия тренда со степенью 2:

GENERATE (ABS(-0.00004#(V$num-TG1)# (V$num-TG1)+0.2#(V$num-TG1)+86)),

(RN2#ABS(-0.00004#(V$num-TG1)#(V$num-TG1)+0.2#(V$num-TG1)+86)/2000).

Конечное время моделирования: 119,0 С. Отклонение от действительного времени: 30,8 С;

• -    логарифмическая линия тренда:

• 3.    Сеанс работы с Блокнотом

GENERATE (ABS(62#LOG(V$num-TG1)-128)),(RN2#ABS(62#LOG(V$num-TG1)-128) /2000).

Конечное время моделирования: 148,3 С. Отклонение от действительного времени: 1,5 С.

Число пакетов 953 шт. Действительное время 15,3 С. Уравнения линии тренда:

• -    полиномиальная линия тренда со степенью 2:

GENERATE (ABS(0.0007#(V$num-TG1)#(V$num-TG1)-0.4#(V$num-TG1)+117)), (RN2#ABS(0.0007#(V$num-TG1)#(V$num-TG1)-0.4#(V$num-TG1)+117)/1000)

Конечное время моделирования: 13 С. Отклонение от действительного времени: 2,2 С;

• -    логарифмическая линия тренда:

GENERATE (ABS (62#LOG (V$num-TG1)-202)), (RN2#ABS (62#LOG (V$num-TG1) -202) /1000).

Конечное время моделирования: 8,7 С. Отклонение от действительного времени: 6,5 С.

Для проверки адекватности эмпирических моделей реальным процессам передачи сетевого трафика по результатам имитационных экспериментов были рассчитаны параметры Херста и определены значения отклонений от практически полученных значений H. Имитационная модель была дополнена блоком, фиксирующим номера пакетов и время их поступления:

SAVEVALUE XN1,(AC1/10000).

SaveValue – запоминает значение AC1 в ячейку XN1. AC1/10000 – переводит единицу времени модели в С. Значения времени, записанные в сохраняемые ячейки, выводятся в текстовый файл. Для передачи данных в среду Fractan была разработана программа-конвертор.

После имитации сеансов взаимодействия пользователя с программами для них определялись значения показателя Херста. Сравнение коэффициентов Херста, полученных на основании результатов имитационного эксперимента, и замеров реального трафика выявило некоторое их различие. Далее приводятся оценки для эмпирических моделей сеансов, которые имеют наименьшую величину расхождения.

На рис 10-12 приведены графики данных test_time_relative для определения параметров Херста эмпирических моделей исследуемого трафика. Для сеанса работы с MS Calculator в качестве наиболее подходящего уравнения автором принята, логарифмическая линия тренда (2), поскольку величина расхождения составила (1,0599/1,0167 -1) ■ 100% = 4,2%.

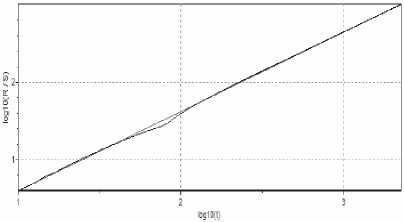
Рис. 10. График данных test_time_relative для модели сеанса взаимодействия с MS Calculator (H = 1,0167±0,0204)

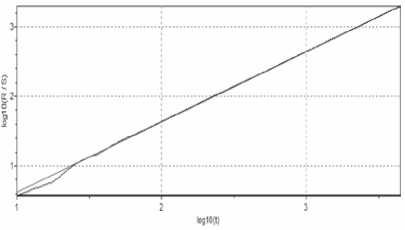
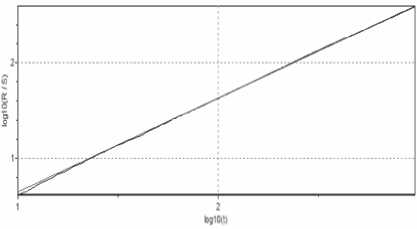
Рис 12. График данных test_time_relative для модели сеанса взаимодействия с блокнотом (H=0.9832±0.0116)

Эти расхождения можно считать незначительными и сопоставимыми с погрешностями экспериментального оценивания. Построенные модели можно применять при моделировании самоподобного трафика информационных систем с трансляцией GUI в потоковом видео для выбранного прикладного программного обеспечения. При этом практически значимыми актуальными задачами могут быть названы задачи проектиро- вания систем облачных вычислений, построения открытых систем.

Выводы

По результатам проведенной работы сделаны следующие выводы:

• -    трафик, порождаемый при передаче GUI в видеопотоке, обладает высокой степенью самоподобия, о чем свидетельствуют найденные значения параметра Херста: H = 1,0599±0,0788 (для сеанса с MS Calculator), H = 1,0679±0,0493 (для сеанса с Paint.NET), H = 1,0083±0,0468 (для сеанса с блокнотом);

• -    для сеанса работы с MS Calculator выбрана логарифмическая линия тренда y = 0,0062ln(x) – 0,0202, с величиной расхождения 4,2%;

• -    для сеанса работы с Paint.NET выбрана логарифмическая линия тренда y = 0,062^.ln(x) – 0,0128, с величиной расхождения 6,5%;

• -    для сеанса работы с блокнотом выбрана полиномиальная линия тренда: y = 7E-08x2 – 4E-05x + 0,0117, с величиной расхождения (1,0083/0,9832 – 1)^.100% = 2,6%.

Построенные модели могут быть использованы для имитации сеансов взаимодействия пользователя с GUI в потоковом видео flv в интересах получения данных о системах обработки графического пользовательского интерфейса в облаке. Полученные результаты применимы в САПР информационных систем для оценки степени загрузки и пропускных возможностях каналов передачи данных, сервера приложений, а также медиасерверов. Методика может быть применена при построения эмпирических моделей для сеансов взаимодействия с другим программным обеспечением.

Перспективным направлением развития результатов данного исследования является технология открытых систем, и в частности вопросы переносимости графического пользовательского интерфейса между программно-аппаратными платформами.