Моделирование трафика терминал-сервера на основе анализа нечетких тенденций временных рядов

Развитие вычислительных сетей (ВС) разного уровня (от локальных до глобальных сетей передачи данных) в последнее десятилетие привело к тому, что качество производственных процессов все более зависит от качества сетевых сервисов. Соответствие масштабов производственных процессов и корпоративной сети может быть достиг- нуто за счет постоянного анализа качества функционирования ВС (в том числе и на прикладном уровне) и прогнозирования ее развития. Такой анализ опирается на результаты моделирования вычислительных сетей как предварительного (на этапе проектирования) так и существующей сети. Модели ВС представляют собой систему, состоящую из компонент: каналы передачи данных, коммутирующее оборудование, и конечные узлы-пользователи. Под узлами-потребителями подразумеваются системы, использующие передающие и коммутирующее оборудование для выполнения своих целей. К ним относятся рабочие станции, серверы,оборудованиеввода-выводаинформации (сетевые принтеры, регистрирующие приборы и т.д.), а так же сети более низкого или высокого уровня, рассматриваемые как одно целое в рамках моделируемой ВС. Одной из задач моделирования является анализ пропускной способности сети (трафик, нагрузка, задержка и т.д.). В этом случае узлы сети выступают в роли генераторов и обработчиков трафика. Если для коммутирующего оборудования существует достаточно много библиотек, позволяющих выполнять имитационной моделирование, то для узлов-пользователей необходимо реализовывать модели в каждом конкретном случаи моделирования. Узел-пользователь является сложной многокомпонентной системой, состоящей из взаимосвязанных объектов: сетевое оборудование, программное и аппаратное обеспечение, внешние источники (пользователи, приборы и т.д.). В работе [1] исходными данными для генерации трафика узлов (моделирования работы) являются:

– генерирование исходящего трафика на основе накопленной статистики работы, экспертной оценки, накопленная статистика в экспертных оценках;

– генерирование исходящего трафика как результата моделирования обработки узлом входящего трафика.

Данные подходы к моделированию узла обладают рядом недостатков. В первом случае невозможно прогнозировать трафик по работе компонент узла. Во втором случае схемы обработки строятся по упрощенным алгоритмам обслуживания и управления очередями, способным описать лишь простые узлы (ftp-серверы, файловые серверы и т.д.), и имеют скорее теоретическую реализацию, чем практическую. На практике, часто, эксперту (пользователю) легче описать работу компонент узла некоторых параметров, которые представляют собой дискретные временные ряды (ВР). При этом параметры описываются не только числовыми значениями, но и экспертными оценками текущего состояния и их динамикой. Зависимость трафика от параметров работы достаточно сложна, поэтому необходимо на основе текущей работы узла (накопленным данным) построить функциональную зависимость, что является объектом анализа ВР.

Временные ряды параметров работы узла имеют ряд особенностей: нестационарность, неоднородность, сложная форма динамики, что ограничивает применимость классических статистических методов анализа ВР, таких как рег- рессионного и спектрального анализа, экспоненциального сглаживания. К тому же в связи со сложной структурой таких рядов не представляется возможным подбор подходящих функций регрессионных, корреляционных, спектральных моделей. В связи с этим на сегодняшний день перспективными технологиями анализа временных рядов являются интеллектуальные методы, позволяющие наиболее полно использовать экспертные знания в процессе построения модели и не имеющие жестких требований к исходным данным.

Интеллектуальные методы анализа временных рядов, используемые для моделирования элементов вычислительных сетей

Наиболее популярными инструментами являются: нейронныесети (НС) и нечеткаялогика.Ис-кусственные НС решают задачу аппроксимации функций нескольких переменных по обучающей выборке путем погружения ВР в многомерное пространство. В качестве модели используется схема на основе разностного уравнения:

yt = f ⁽ yt -1v , yt- d , x t ’•••’ x t - d ) , (1)

где y – зависимая переменная, x – независимые переменные, d – временной лаг. Для анализа используют как стандартную схему персептрона, так и специализированные сетевые структуры с обратной связью [2].

Нечеткая логика, введенная Л. Заде, опирается на интерпретируемые лингвистические описания функциональных зависимостей. В основе лежат понятия нечеткой и лингвистической переменных [3].

Нечеткая переменная (нечеткая метка) характеризуется тройкой (a, U, А), где a - наименование переменной; X – универсальное множество (область определения α ); А – нечеткое множество на U , описывающее ограничения (т.е. Ц а (x)) на значения нечеткой переменной α .

Лингвистической переменной называют набор (в, Т, U, G, M), где в — наименование лингвистической переменной; Т – множество ее значений (терм-множество), т.е. набор нечетких меток; U – универсум; G – синтаксические правила употребления; M – семантические правила употребления.

Введение понятия нечеткой переменной позволяет либо использовать первичную экспертную оценку, либо формировать новые знания о ВР. В зависимости от схемы логического вывода

• [4]    используются следующие нечеткие модели временных рядов (НМВР):

• - схема Суджено (Sugeno)

• ⁽ ~ - 1 ,-~ - d ,~ t ,-~ - d ) ^oR^ y t = f ( y , x ) ; (2)

• -    схема Мамдани (Mamdani)

⁽ y - - 1 ,••• y - d , x t ,- x t -d ) ^o R ^ y_t , (3) где y t , x t - нечеткие временные ряды, R - нечеткое отношение.

Построение нечетких моделей, как правило, основано на настройке функций принадлежностей по параметрам нечетких множеств, используемых в правилах, весов правил (в моделях Суд-жено) и на настройке операций. Если функции принадлежности и операции задаются параметрически, тогда настройка основана на оптимизации этих параметров.

Системы с нечеткой логикой хорошо объясняют получаемые с их помощью результаты, но они не могут автоматически приобретать знания для использования их в механизмах выводов. Поэтому для анализа данных нечеткую логику интегрируют с другими методами, позволяющими выстраивать системы логического вывода. Наиболее часто нечеткие системы представляют многослойными НС, что позволяет использовать методы оптимизации НС (например, метод обратного распространения ошибки), а так же использовать аппаратную реализацию нечетких систем с помощью имеющихся технологий аппаратной реализации НС. В настоящее время разработаны методологии представления и оптимизации нечетких нейронных сетей (ННС) по параметрам функций принадлежности. Примером может служить ставшей уже классической архитектура ANFIS [5]. В работе [6] рассматриваются параметрические классы треугольных операций и предложена архитектура сети по представлению и оптимизации систем Суджено по параметрам операций конъюнкций. Если нечеткие множества, используемые в модели, отражают экспертные знания о моделируемом объекте, то оптимизация только по параметрам операций позволяет сохранить неизменными эти знания. Но возникает проблема интерпретируемости параметрических операций (логических связок).

Ведущей тенденцией в развитии интеллектуальных методов анализа ВР стало использование нечетких характеристик ряда, определенных на некотором интервале времени. В зависимости от предметной области такие характеристики обозначаются разными терминами: динамика, траектория, систематическое движение, поведение, событие и т.д. Таким образом, элементами ана- лиза являются не только пространственные, но и временные изменения значений переменных. Это позволяет интегрировать в модель априорные экспертные знания. Данная идея высказана авторами [2; 7].

В работе [2] анализируется оценка ВР, выра-женнаявлингвистическихтерминах,длячеговво-дятся понятия нечеткого временного ряда (НВР) и нечеткой тенденции (НТ). Нечеткой тенденцией нечеткого временного ряда является нечеткая метка, выражающая динамику (систематическое движение) нечеткого временного ряда. Понятие “тенденция”, моделируемое нечетким множеством, может быть описано набором сконструированных эмпирических правил. Для нахождения нечетких тенденций предлагается использовать ННС. Анализ НТ позволяет на основе динамики процесса прогнозировать поведение временного ряда путем предсказания тенденций развития изучаемого объекта. При этом не предусматривается прогнозирование численных значений ВР, что можно отнести к недостаткам предложенных методов.

В [7] предлагается нечеткая темпоральная модель дляанализа слабо структурированныхрядов. В основе построения модели положено понятие нечеткого темпорального события, характеризующего поведение ВР на временном интервале:

^Ф ( ^t a , t b ) = ⁽ y ^{( t} a , t b ) = q )& ^{(( t} a , t b ) = ^T ) ■

Такое событие имеет смысловое описание «на временном интервале [t a , t b ] с нечеткой продолжительностью т наблюдается тренд временного ряда с нечетким значением q . В качестве инструментов анализа предлагается использовать нечеткие гиперграфы, ННС. Моделью же служит уравнение авторегрессионого типа (1), где переменными выступают нечеткие темпоральные события. Автор рассматривает частные случаи нечетко-темпоральной модели, где каждое событие описывается своим методом расчета. Например, нечеткая переменная «тренд» определяется тангенсом угла наклона прямой линии, аппроксимирующей монотонные участки ВР.

Общим недостатком указанных работ является отсутствие универсального метода построения НМВР. Так же методы построения уравнения нечеткой модели используют архитектуры ННС (или другие алгоритмы) оптимизирующие функции принадлежностей НВР [2] или непосредственно нечеткой интервальной характеристики. Изменение функций в свою очередь меняет смысловую нагрузку нечетких переменных, а так же искажает первоначальные знания, что в условиях анализа экспертных оценок не всегда допустимо.

Формализованная постановка задачи исследования

В данной работе предложена НМВР, реализующая универсальный метод анализа НМВР, и имеющая возможности: описание и распознавание нечеткой интервальной характеристики, построение уравнения модели ВР, получение четкого ВР из нечеткой интервальной характеристики. Задачами исследования являлись формализация НМВР на основе теории нечетких тенденций [2], реализация универсального метода построения НМВР. А так же реализация архитектуры ННС, сохраняющей первоначальные знания в виде лингвистических оценок и формирующей необходимый для аппроксимации состав правил. С помощью предложенных в работе методов проанализирована работа сервера вычислительной сети управления Ульяновского государственного технического университета.

Рассмотрим дискретный временной ряд Y={y t , t – последовательность моментов времени}, y t ∈ U y. .

Определение 1. Нечетким временным рядом Y^~ называется упорядоченная последовательность наблюдений над некоторым явлением, характер которого изменяется во времени, если значения, которые принимает некоторая величина в момент времени, выражена с помощью нечеткой метки:

~ i = «y i . u y , _A ( y, )), t } , где ^~y ⁱ – i - элемент терм-множества лингвистической переменной ( Y , T _y, U _y , G y , M _y ).

Таким образом, НВР представляет собой векторный временной ряд значений всех нечетких переменных:

Y = {~t }, где yt = {y,...,у"}, n — количество терм.

Определение 2. Нечеткая тенденция: пусть y^ = {y 1 ,...,y m } - нечеткий временной ряд лингвистической переменной    ⁽ Y , T y , U у , G у , M у ),

Y _a = {~ _д } - множество нечетких временных рядов одинаковой длины. Тогда нечеткая тенденция ^τ , определенное на Y _Δ есть совокупность упорядоченных пар:

т = {~А, Нт (Уь )Ь где Мт(уд) представляет собой степень принадлежности ~yΔ к НТ.

Данное определение предопределяет НТ как нечеткую переменную. Если говорить о тенден- ции как лингвистической переменной, терм-мно-жеством которой является множество различных интервальных характеристик, наблюдаемых на временном ряду, а универсумом – множество всевозможных функций, тогда НТ определяется:

~

(т ,{т },Ya , Gt , Mt ) , i = 1..p, где ~p – количество видов НТ определенных на ВР, YΔ – множество НВР переменной длины.

Определяя нечеткую тенденцию на всех интервала [ t-m+ 1, t ] временного ряда и позиционируя начало или окончание интервала к временной шкале, получим временной ряд нечеткой тенденции.

Определение 3. Временной ряд нечеткой тенденции (ВРНТ) [8]. Пусть {у& } — множество нечетких временных рядов длиной m , где ~ A t = {~ t - m ₊ i ,-,~ t } , y_t е Y t . Тогда временной ряд нечеткой тенденции есть упорядоченное во времени нечеткое множество:

^т t = {t, Н т < y b t )} .

Для лингвистической переменной НТ временной ряд нечетких тенденций определяется, как векторный ВР значений всех видов НТ:

^т t = ^{{ t} , ^T t ,---, ^T t }•

Предположим наличие зависимости между нечеткими тенденциями, наблюдаемыми в разные моменты времени. Используя схему разностного уравнения (1 ), представим модель временного на основе НТ для одной переменной:

^T t = f ^{( т} t — i ,- ^T t - 1 ) ,                    (4)

где l – временной лаг. Для построения модели ВР на основе НТ необходимо решить следующие задачи:

• -    определить процедуру фаззификации и де-фаззификации ВР;

• -    определить процедуру описания и распознавания НТ;

• -    определить процедуру получения четкого временного ряда из значений НТ;

• -    идентифицировать функциональную зависимость.

Математическая модель временного ряда нечетких тенденций

Получение НВР из четкого ВР основано на операции фаззификации,т.е. перехода от количественных значений к лингвистическим оценкам. Процедура фаззификации достаточно широко описана в литературе [2, 4]. Процесс нахождения степени принадлежности элементов Uy терминальному множеству Ty обозначим функционалом Fuzzy:

Y = Fuzzy [ Y ] .

Функционал предполагает решение задач описания лингвистических терм и правил употребления, выбора соответствующих функций принадлежности. При определении лингвистических термов можно использовать следующие методы: субъективное описание универсума U y на основе экспертных знаний о системе и описательной терминологии, принятой в исследуемой области; равномерное разбиение универсума (как правило, на 3-7 интервалов); кластеризация значений временного ряда для определения наиболее значимых интервалов на универсуме.

Обратная задача фаззификации – дефаззифи-кация, получение четкого ВР из нечеткого задается функционалом deFuzzy :

Y' = deFuzzy [ Y ] .

Задача определения НТ является основополагающей в построении системы анализа данных, решение которой позволит приступить к выявлению связей между параметрами исследуемого объекта. Данная задача состоит из следующих подзадач:

• -    определение лингвистических переменных НТ;

• -    построение временного ряда НТ.

Решение задачи обозначим функционалом Tend :

т = Tend [ Y _A ] .

Для определения лингвистической переменной, выражающей нечеткую тенденцию, требуется выделить типичное поведение нечеткого временного ряда, то есть составить терминальное множество. Анализ исходного ряда для оценки динамики можно производить следующими методами:

• -    использование оценок динамики (рост, падение, стабильность);

• -    субъективное описание на основе экспертных знаний о систематическом поведении параметров системы;

• -    кластеризация значений нечеткого временного ряда для определения наиболее значимых тенденций на универсуме.

Для построения ВРНТ необходимо не только выделить их (обозначить лингвистические термы), но так же дать описание и уметь находить тенденцию на НВР. Таким образом, функционал

Tend включает в себя инструмент описания НТ, алгоритм нахождения соответствия нечетких временных рядов выбранному описанию, то есть алгоритм нечеткого оценивания.

Для анализа и построения четкого ВР по нечеткой модели необходима операция получения НВР из оценки тенденции. Решение данной задачи обозначим функционалом de-Tend , являющимся обратным функционалом Tend :

• Y\ = deTend [ T ] , F\ e Y_& ,

где Y'_a = {у '_д } - множество типичных (характерных) нечетких временных рядов для НТ, имеющих наибольшую степень принадлежности ~

Ц т С у J = ^max A 1) ■ Δ

Использование функционалов дефаззифика-ции deFuzzy, получения нечеткого временного ряда из тенденций deTend решает задачу прогнозирования четкого ВР.

Совокупность компонент и уравнений:

~ = Fuzzy [ y t ] , y_t = deFuzzyty^-.-y tn ], i = 1..n ,

Tt = TendVyt_mj+i,...,yt] , yi = deTend[Tt ,...,t t+m_1 ], m = max(m j), j = 1.. p,

T t = f (t t-VT t-l), где n – количество термов НВР, p – количество термов НТ, mj - интервал определения НТ, l – временной лаг, обозначим моделью нечетких тенденций (МНТ) с характеризующими параметрами (n, р, m, 1). В более подробном виде параметры можно обозначить как (n, {pk}, {mk}, l), где Pk — количество видов тенденций имеющих интервал определения mk.

Рассмотрим частные случаи модели. Модель МНТ \п, р, 1, 1) является, по сути, обычной моделью НВР, использующейся в интеллектуальных методах анализа ВР, например в (2)-(3). Так как НВР – это частный случай ВРНТ, где интервалы определения тенденций единичные. МНТ(п, {p k }, {1, .„}, 1) позволяет включать как моментные, так и интервальные нечеткие характеристики ряда.

Модель нечетких тенденций можно привести к разностному уравнению (1):

^Т t = f ^{( т} t-a ,- ^Т t-l ) ^ ~ t = ^deTend ( f ^{( т} t-a ,- ^T t-l )) ^

^ y t = f l ^{( T} t + m - 1 - a ,- ^{, T} t - l ) ^

^ yt = f2 (yt-1, — , yt-m-l+1) ^ yt = f3 (yt-1,-, yt-m-l+1), при этом a>m, с целью не допущения авторегрессии на текущий и будущий период. В связи с этим отметим следующие моменты:

• -    прогноз ВР отстает от прогноза НТ. Вначале необходимо спрогнозировать НТ на ( m - a -1) вперед, а затем только рассчитать ВР в текущий момент времени;

• -    модель ВР имеет более высокий авторегрессионный порядок, чем МНТ этого же ВР.

Представление модели нечеткой тенденции с помощью нечеткой нейронной сети

Для реализации МНТ можно использовать различные методы и алгоритмы от классического регрессионного анализа до интеллектуальных методов, как для модели в целом, так и для отдельных функционалов. Тем самым представляется возможным комбинировать различные алгоритмы в рамках одной модели. Рассмотрим реализация МНТ на основе методов нечеткой логики.

Нечеткая логика в задаче описания и распознавания НТ позволяет использовать системы логического вывода (далее R ). Эксперту при этом необходимо описать НТ в виде последовательности нечетких меток, которые формируют правила распознавания, что позволяет одновременно описать и дать формулу расчета степени принадлежности четкого ряда к тенденции:

^ т ( Ум ) = Cy t - m + 1 ,--,~ t ) ° R 1 .

Например, нечеткую тенденцию «скачок» можно определить правилом:

«если ( y _t-2 – низкий) и ( y _t-1 – высокий)

и ( y _t – низкий) то τ _t – скачок».

Для анализа и построения четкого временного ряда по нечеткой модели (функционал deTend ) каждому виду нечеткой тенденции сопоставим нечеткий временной ряд, имеющий наибольшую степень принадлежности, в виде правила:

ytt = ^{( t} t ) ° R 2 .

Процедура deTend для приведенного ранее примера, может быть представлена в виде системы обратных правил:

если τ t – скачок, то y t-2 – низкий, если τ t – скачок, то y t-1 – высокий, если τ t – скачок, то y t – низкий.

Уравнение (4) представим также нечетким отношением:

^T t = ^{( t} t₄,-^T t - i ) ° R 3 .

МНТ реализуется многоуровневой системой логических отношений:

R1 ⇒ R3 ⇒ R2 , где выходы в виде нечетких переменных одного набора правил подаются на входы следующего набора правил без дефаззификации и фаззифи-кации. Преобразования в нечеткие и четкие значения происходит только в отношениях R1 и R2 соответственно.

В качестве инструмента построения функциональной зависимости в виде нечетких отношений используем аппарат нечетких нейронных сетей. Особенностью системы логического вывода по нечетким тенденциям при реализации схемы сети является то, что отсутствуют слои фаззи-фикации и дефаззификации, так как входы и выходы – нечеткие значения (в их интерпретации). Используем классические нечеткие нейроны, в которых операции сложения и умножения заменяются треугольными нормами:

И-нейрон в = T ( S ( t 1 , w 1 ), S ( t 2 , w ₂ )) , ИЛИ-нейрон т 0 = S ( T ( в 1 , z i ), T ( в 2 , Z 2 )) .

Что можно интерпретировать в лингвистической форме соответственно как:

если ( τ 1 или w 1 ) и ( τ 2 или w 2 ) то β , если ( β 1 и z 1 ) или ( β 2 и z 2 ) то τ ⁰ .

На основе таких нейронов можно построить сеть логического вывода по Мамдани для нахождения нечеткой тенденции τ добавив весовые коэффициенты. Формализовано такую сеть можно выразить следующим образом: km т0 = S [T(вi, Zi)], вi = T [S(tj, wj,)], i=i                             j=i       j j, где T – оператор конъюнкции, S – оператор дизъюнкции, k – количество правил, m – количество входов. Весовые коэффициенты интерпретируются следующим образом: zi – степень влияния i-ого правила на общий результат (0 – не влияет, 1 – влияет); wji – степени не влияния j-ого входа на i-ое правило (0 – влияет, 1 – не влияет). Основная идея обучения ННС состоит в итерационном процедуре оптимизации весов (zi ,wji) и устранении незначимых связей (сокращении сети), в результате которого формируется необходимый состав и количество правил.

Порядок выявления нечетких зависимостей на основе ННС следующий.

• 1.    Инициализация нейронной нечеткой сети.

• 2.    Обучение: оптимизация весов сети.

• 3.    Анализ сети: сокращение сети.

На этапе инициализации необходимо определить входные переменные: виды тенденций и временной лаг. Сгенерировать избыточное число «полных» правил, включающих в себя все входы, с произвольными весами в интервале (0,1).

Этап обучения – это процесс изменения ве-

сов ННС по обучающей выборке. Обучение сети

возможно методом обратного распространения

ошибки, для этого определим функцию ошибки

E = 2( т 0 - т ) ²

, которую необходимо минимизи-

ровать методом снижения градиента. Для уменьшения квадратичной ошибки E необходимо изменять веса ( z_i ,w_ji ) в направлении антиградиента функции E :

+1

w . . w j,i

= wi, J

- η

∂E dwj,i

+1

, z_i

= zi

∂E

-

η , ∂z i

где η – скорость обучения, с ограничением W + 1 G [0,1] , z ^{+ 1} G [0,1] . Для вычисления производной ошибки необходимо выбрать соответствующие функции t-норм и t-конорм. Признаком окончания обучения является достижение уровня ошибки.

На этапе анализа осуществляется обработка ННС с целью ее упрощения. В основе алгорит-

• -    реализация функционалов модели Fuzzy, de-Fuzzy , Tend, deTend ;

• -    реализация основного уравнения модели (4), оптимизация на основе методов нейронных сетей;

• -    прогнозирование временных рядов на заданный интервал;

• -    графическое отображение всех временных рядов: исходных, нечетких переменных, нечетких тенденций;

• -    сохранение сформированной модели во внешнем файле в формате XML (Extensible Markup Language).

В основе программы лежит иерархическое представление проекта (рис. 1), которое одновременно является представлением внутренней программной реализацией на основе ООП и форматом хранение в XML-файле.

мов сокращения лежит принцип удаления незначимых связей и нейронов из сети. Одним из простейших методов сокращения является метод проекций, который реализуется следующим образом. Синоптический вес обнуляется, если его значение попало в заданный диапазон:

1, wj,i > (1 - 8)        Г 0, z < e wj,i = 1------------------, zi = 1-----------, wj,i,wj,i < 8          I zi, zi > e

где ε – некоторая константа. На основе выбранного уровня весов ε удаляются связи «вход – И-нейрон» при w_j,i = 1 и «И-нейрон – ИЛИ-нейрон» при z i = 0. Так же удаляются неиспользуемые входы и правила.

В результате получается система логического вывода, являющейся объясняющей функцией в модели временного ряда. Нечеткие продукции легко интерпретируются для эксперта, так как выражены в терминах, присущих исследуемой области, и отсутствуют скрытые нелинейные связи.

Программная система анализа нечеткого временного ряда

Дляанализавременныхрядовпопредложенной модели нечеткого временного ряда создано программное обеспечение FuzzyTend-Net. Программа написана в среде Microsoft Visual Basic. NET и для запуска скомпилированной версии требуется Microsoft .NET Framework 1.1.

Основные задачи, решаемые системой:

- многомерный анализ данных с несколькими входными и выходными переменными;

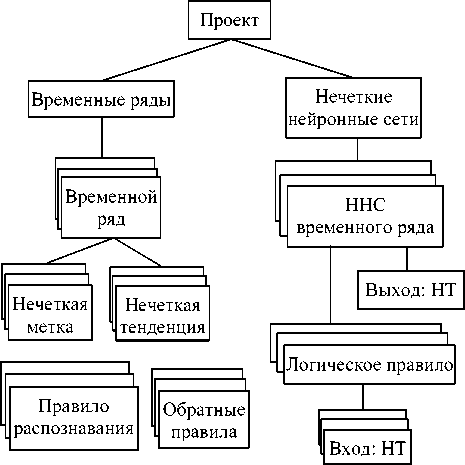
Рис. 1. Структура данных проекта

Таким образом,каждому временному ряду пользователь устанавливает множество лингвистических термов с соответствующими функциями принадлежностями (используется трапециевидная форма функции) и множество нечетких тенденций. Возможность использования нескольких правил распознавания и обратных правил для каждой тенденции позволяет достаточно гибко описывать разнообразные интервальные экспертные оценки.

Уравнение модели временного ряда представляет собой нечеткую нейронную сеть, содержащую подсети для каждой выходной тенденции. Каждая подсеть это система логического вывода, состоящая из множества

правил.Данные правила можно формировать вручную и в автоматическом режиме с оптимизацией на основе алгоритма обратного распространения ошибки. Для сокращения сети используется метод проекций. Логические связки (функции треугольных норм) используются следующие: для правил распознавания и обратных правил – минимум и максимум,для ННС – произведение и вероятностная сумма.

Сохранение сформированной модели во внешнем файле в формате XML позволяет не только в дальнейшем продолжить рассмотрение модели, но использовать модель в другом программном обеспечении.

Моделирование терминал-сервера на основе временного ряда нечетких тенденций

На основании рассмотренной модели проанализирована работа одного из узла вычислительной сети УлГТУ. Узлом является сервер под операционной системой Microsoft Windows 2003, выполняющий приложения в терминальном режиме. Основное пользовательское приложение: базы данных «1С: Предприятие», работающее в файл-серверном режиме, где данные расположены на этом же сервере.

Таблица 1. Описание переменных

Параметр	Описание
X 1 - Память \ Обмен страниц в сек	Число страниц (из оперативной памяти), прочитанных с диска или записанных на диск
X 2 - Обращений записи на диск/сек	Частота выполнения операций записи на физический диск
X 3 - Обращений чтения с дис-ка/сек	Частота выполнения операций чтения с физического диска
X 4 - % загруженности процессора	Доля времени, которую процессор тратит на обработку всех потоков команд
X 5 - Операции чтения	К К о о л л и и ч ч е е с с т т в в о о о о б б ъ ъ е е к к т т о о в в о о т т к к р р ы ы т т ы ы х х д д л л я я п п р р о о с с м м о о т т р р а а в в П П О О 1 «1 С С :П : р П е р д е п д р п и р я и т я и т е и , е», о о п п р р е е д д е е л л я я е е т т с с я я и и з з л л о о г г о о в в в в с с е е х х б б а а з з д д а а н н - - н н ы ы х х, у у с с т т а а н н о о в в л л е е н н н н ы ы х х н н а а се с р ер ве в р ер е е
X 6 - Операции записи	К Ко о л ли и ч ч е е с с т т в в о о о о б б ъ ъ е е к к т т о о в в, з з а а п п и и с с а а н н н н ы ы х х в П в О ПО 1С « : 1 П С р : е П дп р р е и д я п т р и и е я , т о и п е р » е , д о е п л р я е е д т е с - я и л з яе л т о с г я о и в з в л се о х го б в аз вс д е а х нн ба ы з х д у а с н т н а ы но х в , -л у е с н та н н ы о х вл н е а н с н е ы рв х е н р а е сервере
Y - Трафик	Количество байт, которое сервер послал или получил через сеть

Таблица 2. Описание тенденций изменений пара- метров модели терминал-сервера

я С	НВР	ВРНТ
	y A, B, C, D	τ	Tend
			deTend
X 1	низкое -1, 0, 0.5, 9.5	простой	низкое(1) &низкое(2) Х
	высокое 0.5, 9.5, 30, 31	загрузка	высокое(1) &высокое(2)
			Х
X 2	низкое -1, 0, 0.5, 9.5	простой	низкое(1) &низкое(2) Х
	высокое 0.5, 9.5, 20, 21	загрузка	высокое(1) &высокое(2)
			Х
X 3	низкое -1, 0, 0.5, 9.5	простой	низкое(1) &низкое(2) Х
	высокое 0.5, 9.5, 20, 21	загрузка	высокое(1) &высокое(2)
			Х
X 4	низкое -1, 0, 1, 24	простой	низкое(1) &низкое(2) Х
	высокое 1, 24, 50, 51	загрузка	высокое(1) &высокое(2)
			Х
X 5	низкое -1, 0, 0.5, 1.5	простой	низкое(1) &низкое(2) Х
	высокое 0.5, 1.5, 10, 11	загрузка	высокое(1) &высокое(2)
			Х
X 6	низкое -1, 0, 0.5, 1.5	простой	низкое(1) &низкое(2) Х
	высокое 0.5, 1.5, 10, 11	загрузка	высокое(1) &высокое(2)
			Х
Y	низкое -1450, -50, 50, 1450	простой	низкое(1) &низкое(2) про-стой(t)⇒низкое(t) про- стой(t+1)⇒низкое(t)
	высокое 50, 1450, 1550,	загрузка	высокое(1) &высокое(2)
	2950		загрузка(t)⇒ высо-ко t е ) (t) загруз- ка(t+1)⇒высокое(t)
		рост	низкий(1) &высокое(2)
			рост(t)⇒высокое(t); рост(t+1)⇒низкое(t);
		падение	высокое(1) &низкий(2)
			паде- ние(t)⇒низкое(t); па п д а е д н е и - е ние(t+1)⇒высокое(t) ; ;

Администратор ВС может описать работу программного и аппаратного обеспечения, описать же работу сетевого оборудования (трафик) затруднительно. Определить зависимость объема трафика от работы приложений, выполняющихся на сервере, и работы пользователей так же затруднительно, так как отсутствует прямая связь между данными элементами. Но для проектирования общей ВС необходимо не только построить модель узла, генерирующего определенный трафик, но смоделировать ситуации при различных режимах работы программного приложения. Были выбраны параметры работы (см. таблицу 1) и собрана статистика с 15-секундным интервалом в течение одного дня.

Анализ производился в программе Fuz-zyTendNet. Для всех параметров установлены нечеткие переменные НВР, описывающие значения: «высокое», «низкое». Установлены нечеткие тенденции: «загрузка», «простой». Для трафика так же определены дополнительные нечеткие тенденции: «рост», «падение». В таблице 2 представлены описание функционалов МНТ. Отметим следующие:

• -    функционал deTend описан только для зависимой переменной (трафика);

• -    в модели используются НТ, определенные на единичном интервале, которые имеют смысловую нагрузка аналогичную переменным НВР.

Для сравнения моделей на основе нечеткого временного ряда и нечетких тенденций был проведен ряд экспериментов (табл. 3). Анализировались модели МНТ ( n, p, m, l ) от самого простого случая (МНТ (2, 2, 1, 2) – нечеткая модель вида ( х )) до моделей, включающих в себя как НВР, так и ВРНТ (МНТ(2, {2, 4}, {1, 2}, 2).

Таблица 3. Результаты обучения ННС.

Вариант				Средняя ошибка варианта
№	Вход		Выход
	m x	m y	m y	САО	СКО
1	1	-	1	283,80	187985,80
2	1	1	1	256,62	168378,57
3	1	-	2	264,69	168098,40
4	1	-	2, 1	279,25	169740,03
5	1	1	2, 1	273,89	156039,60
6	2	-	1	241,67	188527,43
7	2	1	1	222,07	139806,37
8	2	-	2	233,96	176264,90
9	2	-	2, 1	235,77	172960,83
10	2	1	2, 1	234,64	146154,73

Таким образом, комбинируя интервалы НТ входныхивыходныхпеременных m =(1, {1, 2}, 2), получали разные варианты уравнения для сравнительного анализа. В таблице 3 представлены результаты обучения ННС, где каждый вариант рассчитывался три раза для разных случайных начальных весов. Ошибка рассчитывалась как ошибка прогноза на один шаг вперед на тестовой выборке (САО – средняя абсолютная ошибка, СКО – средне-квадратическая ошибка).

Сравнивая варианты (1-5) с моментными экспертными оценками на входе и варианты (6-10) интервальными оценками, можно сделать вывод, что модель на нечетких тенденциях описывает моделируемый процесс более успешно. На рис. 2 представлен прогноз на шаг вперед для двух моделей (варианты 2 и 7).

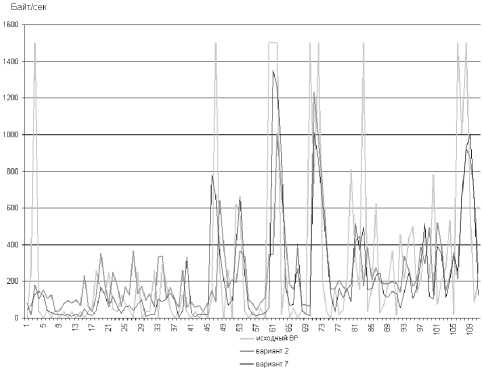
Рис. 2. График тестируемого и прогнозных ВР

В результате мы получили функциональную зависимость, которая не только хорошо описывает работу сервера,но и дает лингвистическую интерпретацию зависимости. Уточнить модель зависимости можно, удалив связи в сети ниже заданного уровня (например, 0.5) и убрав влияние весов. Так если правила вида «если (рост или 0.2) и (падение или 0.7) то (высокий и 0.9)» эксперт возможно будет считать плохо трактуемые, то правило «если падение то высокий» достаточно хорошо объясняет работу узла. На рис. 3 показана модель с «повышенной интерпретируемостью» для варианта 7. Так же отметим, что для НТ получилось меньше правил, чем для НВР. Так, например, тенденция загрузки трафика определяется 3-4 правилами в зависимости от эксперимента, когда как просто высокий трафик – 7-8 правил. В частности, тенденция загрузки трафика объясняется следующими причинами:

• -    загрузка на обращение записи к диску в текущий момент;

• -    загрузка на обращение чтения с диска в предыдущий момент и загрузка на обращение записи к диску в текущий момент;

• -    длительная загрузка на обращение записи.

Для моделирования объема трафика сервера экспертом были предложены и описаны следующие режим работы сервера: ввод данных, чтение данных, формирование отчетов, – с высокими значениями соответствующих групп параметров. На рис. 4 представлены результаты моделирования.

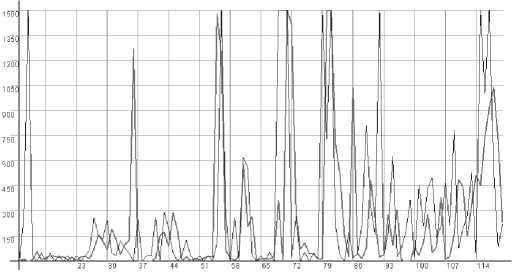
Рис. 3. График тестируемого ВР и упрощенной НМВР

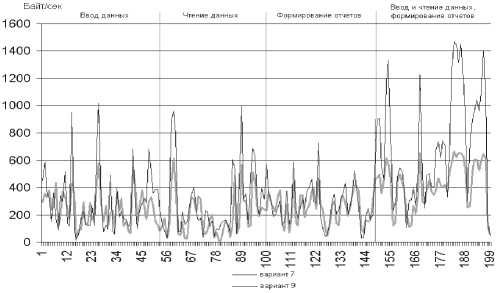
Рис. 4. Моделирование нагрузки

Заключение

Таким образом, временной ряд нечетких тенденций является результативным индикатором развития моделируемого процесса в сложной технической системе, описанного качественно, в лингвистических терминах. Базовыми операциями обработки нечетких тенденций являются алгоритмические операции обработки нечетких тенденций,а именно операция формирования временного ряда нечетких тенденций по исходному временному ряду и обратная операция генерации ряда – представителя нечеткой тенденции. Нечеткая нейронная сеть предложенной архитектуры является эффективным генератором правил распознавания нечетких тенденций. Разрабо- танная математическая имитационная модель терминал сервера, как элемента вычислительной сети,на основе временных рядов нечетких тенденций позволяет прогнозировать загрузку процессора, исходящий и входящий трафик сервера.