Моделирование трехмерного устройства нанофотоники для ввода излучения в планарный волновод

С помощью программы FullWAVE (, в которой реализован разностный FDTD-метод решения уравнений Максвелла, промоделировано трехмерное устройство нанофотоники, состоящее из субволновой дифракционной решетки, широкого и узкого планарных волноводов и фотонно-кристаллической линзы Ми каэляна, расположенных в тонкой пленке кремния на подложке из трех периодов зеркала Брегга, каждый период которого состоит из слоя кремния и плавленного кварца. Устройство предназначено для ввода лазерного пучка с фокусным пятном 3 × 4,6 мкм2 с длиной волны 1,55 мкм в узкий планарный волновод шириной 500 нм, что приводит к «сжатию» площади сечения входного пучка в 125 раз. Моделирование показало, что эффективность устройства равна 32% от энергии сфокусированного на решетку линейно поляризованного эллиптического гауссова пучка и 52%, если решетку осветить участком плоской волны. Для сравнения, если вводить свет в это же устройство, но без решетки, а фокусируя свет на торец кремниевой пленки широкого волновода, то эффективность будет равна только 8%.

Для решения задач нанофотоники, которые имеют место в телекоммуникационных технологиях, многие устройства реализуются с помощью планарной технологии кремний-на-изоляторе, аналогично интегральным электронным чипам [1]. При этом свет распространяется в проволочных световодах с шириной 450 нм, выполненных на пленке кремния толщиной 220 нм, или проходит через 2D фотоннокристаллический волновод шириной 300-500 нм. Свет доставляется к устройствам нанофотоники с помощью одномодового волокна, диаметр сечения которого равен 9 мкм. Поэтому, если просто прислонить торец волокна к торцу планарного волновода, то в него войдет около 0,1% световой энергии моды волокна. Поэтому обычно на пленке кремния делают одномерную субволновую дифракционную решетку с периодом 580-600 нм и глубиной канавок около 50 нм, площадь решетки 10×10 мкм [2]. Двумерное моделирование такой бинарной решетки на кремнии с подложкой из кварца дает эффективность 28% [2]. Известны наклонные решетки на индиифосфате, у которых теоретическая эффективность достигает 59%, а эксперимент показал 30% [3]. В [4] используется дополнительная линза для фокусировки выходящего из волокна излучения на дифракционную решетку. При этом расчетн ая эффективность (2D моделирование) ввода была 67,6%, а экспериментальная – только 28%. Структура в [4] была с антиотражающим покрытием. Если в промежуток межд у слоями кварца и кремния напылить тонкую пленку золота (зеркало), то эффективность ввода ув еличивается до 72% [5]. В этой же работе была создана такая решетка в широком планарном волноводе из кремния. Эксперимент показал, что эффективность такого устройств а была равна около 70%, что хорошо согласуется с расчетом.

Однако ввести излучение в широкий волновод (ширина около 10 мкм или около 4 мкм, если использовать линзу для фокусировки) – это только часть задачи. Другая ее часть заключается в сопряжении моды широкого волновода с модой узкого волновода. Для такого сопряжения можно использовать либо планарные тейперы (сужающиеся волноводы) [6], либо планарные фотонно-кристаллические линзы [7-10]. Недостатком сужающихся волноводов является относительно большая их длина 30-130 мкм. Рассмотрим подробнее методы ФК-линз. В [7] с помощью 2D-моделирования FDTD-методом исследовались ФК-линзы для длины волны λ = 1,55 мкм на кремнии из N×M = 25×8 отверстий с периодом a = 0,28 λ , радиусы отверстий увеличивались от оси линзы ( r = 0,27 a ) к периферии ( r = 0,39 a ). Показано, что на фокусном расстоянии 28,6 a для линзы толщиной 9 a , освещенной гауссовым пучком с диаметром перетяжки 25 a , получается фокусное пятно, диаметр которого по полуспаду интенсивности равен FWHM = 0,54 λ . Моделирование также показало, что эффективность ввода, если в области фокуса разместить планарны й волновод шириной 2 a , будет равна 60%.

В [8] аналогично [7] моделировалась 2D ФК-линза, сформированная в кремнии (n = 3,46) с помощью периодических отверстий (период a) с радиусами r(x) от 0,25a до 0,40a. Особенностью этой линзы является то, что радиусы растут от оси к пе- риферии линзы по закону r(x) ~ x1,4. Именно при таком законе роста наблюдается наименьший размер фокусного пятна FWHM = 1,27λ. При этом линза освещалась гауссовым пучком диаметром 26a, фокусное расстояние было 10a, а период решетки отверстий был равен a = 0,26λ . В работе [8] также показано, что хроматическая аберрация ФК-линзы такая же по знаку, как и у дифракционной решетки: фокусное расстояние растет с ростом частоты света.

Моделирование в [7, 8] было проведено для TE -поляризации (электрический вектор E был в плоскости ФК-линзы). В [9, 10] рассмотрена ФК-линза Микаэляна, которая отличается от ФК-линз в [7, 8] тем, что фокусирует свет вблизи своей поверхности, и поэтому, во-первых, с помощью такой линзы можно формировать безаберрационное фокусное пятно с диаметром, меньшим, чем дифракционный предел (так как в формировании фокусного пятна принимают уч астие поверхностные волны), а во-вторых, узкий сопрягаемый волновод можно приблизить вплотную к линзе.

В данной работе приводятся результаты трехмерного моделирования полного устройства сопряжения, включающего и решетку для ввода сфокусированного гауссова пучка в широкий планарны й волновод, и ФК-линзу Микаэ ляна для согласования мод широкого и узкого волноводов. В работе с помощью программы FullWAVE показано, что эффективность такого устройства нанофотоники составляет 32%, и при этом происходит «сжатие» площади сечения гауссова пучка (3 × 4,6 мкм) в площадь моды узкого волокна (0,22 ×0,5 мкм) в 125 раз. Если осветить дифракционную решетку участком плоской волны, то эффективность повышается до 52%. Причем эффективность ввода решеткой сфокусированного гауссова пучка в широкий планарный волновод равна 62,5%, а эффективность сопряжения широкого (4,6 мкм) и узкого (0,5 мкм) волноводов с помощью ФК-линзы Микаэляна равна 46%. Для плоской волны две последние цифры увеличиваются соответственно – 78% и 67%.

2.    Двумерное моделирование ввода света в планарный волновод с помощью решетки

На рис. 1 показана 2D-схема ввода света в тонкий планарный волновод с бинарной решеткой (ширина штрихов равна ширине канавок) на тонкой подложке. Вдоль оси Y волновод, штрихи решетки и подложка имеют неограниченные размеры. Подложка имеет многослойную структуру (3 периода зеркала Брегга) для увеличения эффективности ввода света в волновод. Параметры структуры на рис. 1 подобраны квазиоптимальным образом путем перебора. Материалы выбраны согласно широко применяемой технологии кремний-на-диэлектрике.

Волновод был из кремния (Si) с показателем преломления n 1 = 3,479 для длины волны света λ = 1,57 мкм, толщиной h = 220 мкм на кварце (SiO 2 ) с показателем преломления n 2 = 1,44 и шириной

W 1 = 1,03 мкм. Далее в подложке опять идет слой кремния шириной W 2 = 0,55мкм. Эти два слоя в подложке (кремний + кварц) толщиной W 1 + W 2 повторяются еще два раза. При добавлении четвертого периода такого зеркала Брегга эффективность ввода света в волновод не увеличивалась. На пленке кремния имеется субволновая поверхностная бинарная дифракционная решетка с периодом T = 750 нм, глубин а канавок решетки D = 90 нм. Рабочая длина решетки 7-8 периодов. Свет в виде цилиндрического гауссова пучка TM -поляризации (вектор электрического поля направлен вдоль штрихов решетки и вдоль оси Y, при TE -поляризации свет почти не вводится в волновод). Радиус гауссова пучка по оси Z равен b = 3 мкм. Центр п еретяжки гауссова пучка расположен на расстоянии от решетки (по оси X) d 1 = 2,78 мкм и на расстоянии от края решетки (по оси Z) d 2 = 4,15 мкм. Угол падения лазерного пучка

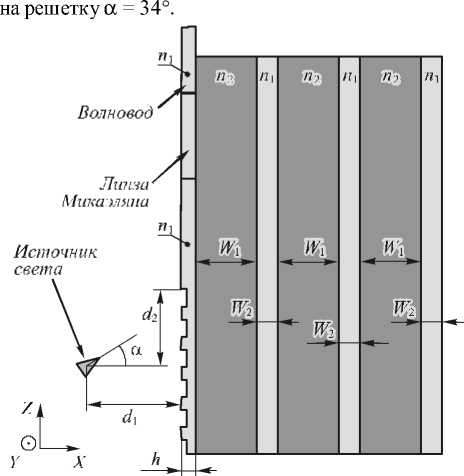
Рис. 1. Двумерная схема ввода света TM-поляризации (E_y ≠ 0 ) в кремниевый волновод с помощью бинарной поверхностной субволновой дифракционной решетки

Моделирование проводилось программой FullWAVE 6.0 (фирмы RSoft, США), в которой реализован разностный FDTD-метод решения системы уравнений Максвелла. В нашем случае при приведенных выше параметрах эффективность ввода света в волновод с помощью решетки составила η = 66,3%. Под эффективностью здесь понимается отношение мощности (или суммарной интенсивности) моды волновода к мощности гауссова пучка, умноженное на 100%.

Моделирование в этой работе проводилось при след ующих параметрах сетки: шаги по осям X и Y были равны λ / 87, шаг по продольной оси Z был равен λ / 78, а шаг по временной шкале выбирался равным сT / 196, где с – скорость света в вакууме, T – период колебаний св етовой волны. Толщина поглощающего слоя со всех сторон области расчета была равна 0,5 мкм. В Таблице 1 приведена зависимость эффективности ввода от шагов дискретизации. Видно, что при выбранных значениях полученная эффективность устойчива к изменениям сетки (предпоследняя строка Таблицы 1).

Таблица 1. Зависимость эффективности ввода света в волновод от выбранных параметров сетки

A x	A z	A t	п, %
X / 20	X / 20	сT / 64	22
X / 30	X / 30	сT / 80	52
X / 40	X / 40	сT / 80	63
X / 50	X / 50	сT / 100	65
X / 87	X / 78	сT / 196	66,3
X /100	X /100	сT / 200	67

На рис. 2 показана зависимость эффективности п от толщины слоя кварца W 1 в подложке – зеркале Брегга на рис. 1. Из рис. 2 видно, что имеют место резонансны е (узкие) пики отражения (как в зеркале Брегга или 1D фотонном кристалле) при W 1 = 0,47 мкм, 1,03 мкм и 1,6 мкм. Максимальная эффективность достигается при W 1 = 1,03 мкм.

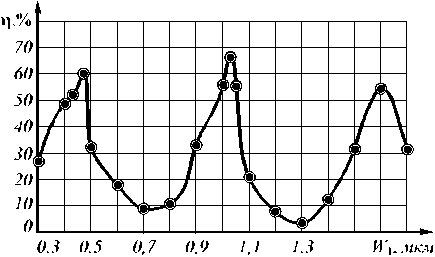
Рис. 2. Зависимость эффективности п ввода в 2D волновод от толщины слоя кремния W₁ в подложке

На рис. 3 показан результат моделирования ввода света в 2D волновод: показана мгновенная картина амплитуды электрического поля E y ( x , z ) . Из рис. 3 видно, что гауссовый пучок затухает при прохождении внутрь подложки и за три периода зеркала Брегга почти не проникает. Зеркало Брегга работает, так же как антиотражающее покрытие, и поэтому гауссов пучок почти не отражается от решетки, а эффективно вводится в пленку кремния.

На рис. 4 показана зависимость эффективности ввода сфокусированного гауссова пучка в волновод в 3D случае при увеличении толщины h2 волновода (рис. 1) вдоль оси Y. Из рис. 4 видно, что при толщине волновода и решетки h2 = 4,6 мкм достигается эффективность п = 60%, а при толщине h2 = 8 мкм эффективность ввода п = 65% будет немного меньше, чем эффективность в 2D случае п = 66,3%. Дальнейшее увеличение толщины h2 устройства (рис. 1) не моделировалось из-за ограниченного объема оперативной памяти компьютера. Таким образом, 3D моделирование с помощью программы FullWAVE показало, что 60% световой энергии сфокусированного на решетку гауссова пучка (площадь перетяжки 3 × 4,6 мкм) можно ввести в планарный кремниевый волновод (рис. 1) шириной 4,6 мкм.

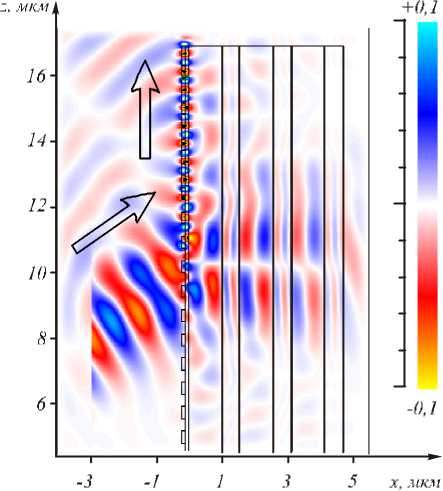
Рис. 3. Мгновенное распределение амплитуды Ey ( x , z )

(стрелками показано направление распространения

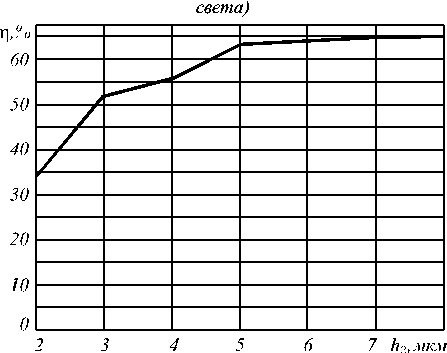
Рис. 4. Зависимость эффективности п ввода в 3D волновод от толщины волновода h₂ в третьем измерении вдоль оси Y

• 3.    Трехмерное моделирование фотонно-кристаллической линзы Микаэляна для сопряжения двух волноводов

В [10] была промоделирована 2D ФК-линза Микаэляна, соединяющая два планарных волновода в кремнии толщиной 5 мкм и 0,5 мкм. Эффективность связи была равна п = 45%. В этом разделе приводятся результаты трехмерного моделирования аналогичного устройства нанофотоники.

На рис. 5 показана схема планарных волноводов, сопряженных с помощью ФК-линзы. Ширина входного волновода – 4,6 мкм, выходного – 0,5 мкм, толщина пленки кремния – 220 нм, показатель преломления n = 3,47 для длины волны X = 1,55 мкм, коли- чество отверстий – 12 × 17, диаметр отверстий от 186 нм на оси линзы до 240 нм на периферии, период решетки отверстий – 250 нм. Подложка из кварца с показателем преломления 1,44 и имеет толщину 1 мкм. На вход широкого волновода подавался TE-поляризованный свет (электрический вектор E лежит в плоскости ФК-линзы) эллиптического гауссова лазерного пучка с радиусами по осям X и Y 4,6 мкм и 0,22 мкм. Полная 3D область расчета программой FullWAVE была равна X × Y × Z = 6 × 3,1 × 9 мкм3. Расчет составляющих электромагнитного поля для устройства нанофотоники, показанного на рис. 5, занял примерно 18 минут на процессоре Intel ® Celeron ®, 3,06 ГГц, ОЗУ 512 Мб.

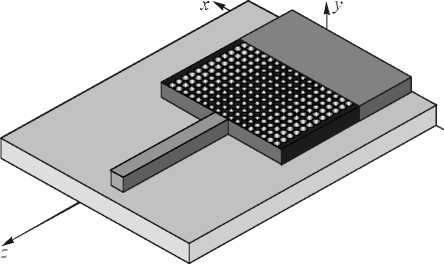
Рис. 5. 3D схема двух планарных кремниевых волноводов (темно-серый), сопряженных ФК-линзой (черный) на подложке из кварца (светло-серый)

Эффективность связи между двумя волноводами (рис. 5) составила п = 46%. Это почти совпадает с эффективностью в двумерном случ ае [10]. В обоих случаях, в этой работе и в [10], Френелевское отражение не учитывалось. Такое совпадение результатов говорит о том, что трехслойная подложка подобрана так, что свет почти не покидает волноводы и линзу в направлениях «вверх» и «вниз» по оси Y, а только отражается от границ раздела сред и уходит из линзы мимо волновода в плоскости XZ, как и в двухмерном случае.

Если заменить гауссов пучок на участок плоской волны площадью 4,6 × 0,22 мкм2, которая освещает торец входного волновода, то эффективность связи (без учета Френелевского отражения от торца волновода) возрастает до 67%. Такое увеличение эффективности связи объясняется тем, что плоская волна фокусируется линзой Микаэ ляна в пятно меньшего диаметра, чем гауссовый пучок такого же размера. А фокусное пятно меньшего диаметра эффективней «переходит» в моду узкого волновода.

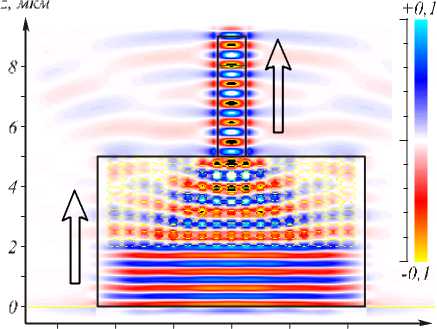
На рис. 6 показан результат моделирования устройства нанофотоники, показанного на рис. 5, при освещении широкого волновода гауссовым пучком с перетяжкой 4,6 × 0,22 мкм2.

Из рис. 6, на котором показано мгновенное распределение амплитуды Ex (x, y, z), видно, что свет распространяется внутри волновода и за его границы (в подложку) выходит только малая часть световой энергии. Большая часть из потерянной энергии отражается от границы ФК-линзы и уходит назад в широкий волновод. Видно также, что в узком волноводе потери (уход света в подложку) больше, чем в широком.

б)

Рис. 6. Мгновенное распределение амплитуды Ex ( x, y, z ) в плоскости ZX (а) и плоскости ZY (б), вертикальная линия (б) показывает границу подложки, стрелками показано направление распространения света

4.    Трехмерное моделирование всего устройства нанофотоники

На рис. 7 показана 3D схема всего устройства нанофотоники, которое включает решетку, ФК-линзу Микаэ ляна и два сопрягаемых планарных волновода. На подложке (три периода зеркала Брегга) из кремния и кварца расположена тонкая пленка (толщиной 220 нм) кремния шириной h 2 = 4,6 мкм в области поверхностной решетки, линзы и широкого волновода и шириной s = 0,5 мкм в области выходного узкого волновода. Длина всего устройства 17 мкм. Для ФК-линзы l m = 3 мкм, промежуток волновода межд у решеткой и линзой l = 4 мкм (в еличи-на этого участка не сильно влияет на эффективность, и его длину можно менять). На устройство (рис. 7) под углом 34° в области решетки падает эллиптический гауссов пучок с линейной поляризацией (электрический вектор имеет только одну проекцию E x ) с площадью перетяжки 3 × 4,6 мкм² (в этом случае эффективность максимальная).

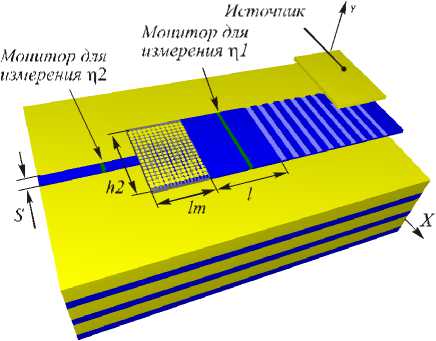
Рис. 7. Схема всего устройства нанофотоники, включающего решетку, широкий волновод, ФК-линзу, узкий волновод и подложку – зеркало Брегга

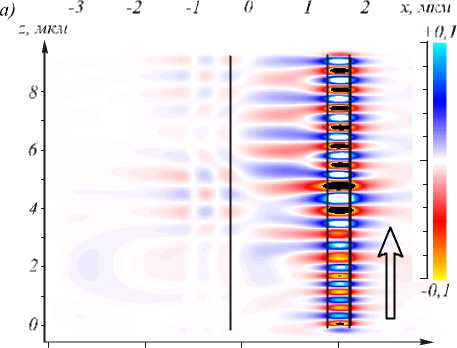
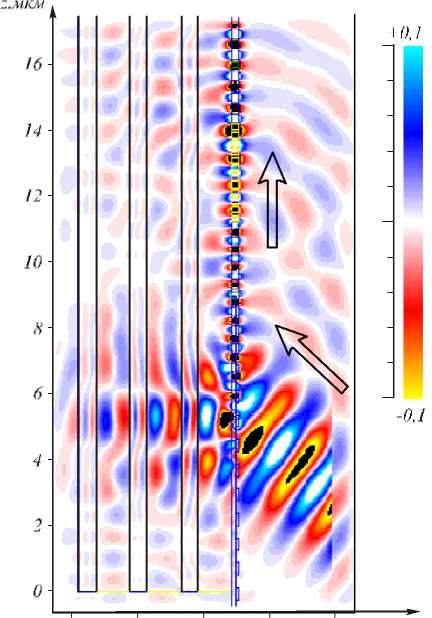
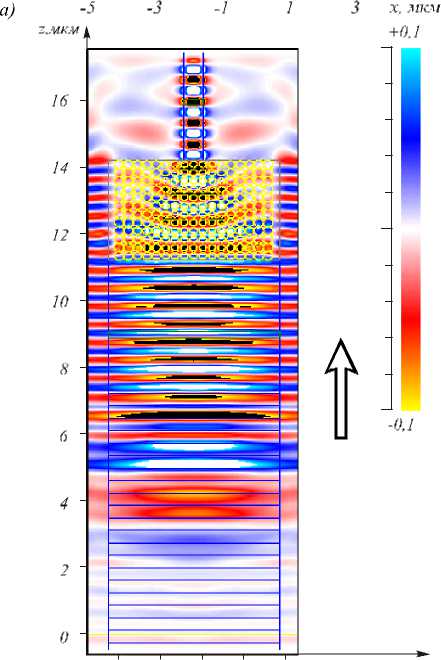
На рис. 8 показано мгновенное распределение амплитуды электрического поля E x (x, y, z) в плоскости ZY (а) и плоскости ZX (б).

Из рис. 8 видно, что свет проходит в подложку под решеткой, а под волноводом и линзой почти не рассеивается в подложку.

Эффективность ввода света в волновод решеткой (рассчитанная в широком волноводе после решетки) составила η 1 = 62,5% от полной световой мощности гауссова пучка (в этот раз эффективность дана с учетом и Френелевского отражения от решетки), а эффективность всего устройства (рассчитанная на выходе узкого волновода) равна η 2 = 32%. Если то же устройство (рис. 7) осветить участком плоской линейно-поляризованной волны с площадью сечения 3 × 4,6 мкм², то эффективность увеличивается: η 1 = 78% и η 2 = 52%. Заметим для сравнения, что если сфокусировать тот же гауссов пучок на торец широкого волновода устройства на рис. 5 (без решетки), то эффективность будет всего η = 8%.

5.    Заключение

В работе получ ен следующий результат. Строгое трехмерное мод елиров ание с по мощью про -граммы FullWAVE нового устройства нанофото -ники, содержащего субволновую б инарную ди-фракцио нную решетку с периодом 750 нм, планарны е широкий волновод (4,6 мкм) и узкий волновод (0,5 мкм), связанные ФК-линзой Микаэля на (размер линзы 3 × 4,6 мкм², матрица отверстий 12 × 17 с периодом 250 нм), выполненных на пленке кремния толщиной 220 нм, нанесенной на поверхность подложки, состоящей из трех перио -дов зеркала Брегга (слои кремния и кв арц а с периодо м 1,58 мкм), по казало, что при фокусировке под уг лом 34° на решетку гауссов а эллиптического пучка с TE -поляризацией (сеч ение перетяжки 3 × 4,6 мкм), эфф ективно сть всего устройства равна 32%, что в 4 раза больше, чем при фокусировке того же гауссов а пучка на то рец широкого во лно -вода без д иф ракционной решетки.

-2    -1 О I 2              v^ku

Рис. 8. Мгновенное распределение амплитуды электрического поля Ex(x, y, z) для всего устройства: в плоскости ZY (а) и плоскости ZX (б), стрелками показано направление распространения света

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08014-1 и Y4-P-14-04), гранта Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9) и грантов РФФИ 08-07-99007 , 09-07-0000, 09-07-00145.