Моделирование турбулентности вращающегося дугового потока плазмы в канале с кольцевыми электродами

восходящей вольтамперной характеристике. Изучение закономерностей развития дуги в подобных устройствах представляет интерес для понимания механизмов генерации турбулентности и установления роли неравновесных явлений при формировании пленки напыления дуговым потоком плазмы.

Основой моделирования электрической дуги в потоке газа являются уравнения магнитной газовой динамики (МГД) [1]. Для описания неравновесной плазмы хорошим приближением является двухтемпературная модель [1], а турбулентного режима течения – двухпараметрическая k-ε модель турбулентности [7-8]. Неравновесность плазмы в значительной мере определяется силой тока и давлением [9]. Существенное влияние на режим плазменного напыления оказывают расход газа, способ его подачи в канал, геометрия разрядной камеры [1-4]. В данной статье предлагается математическая модель расчета характеристик электрической дуги в канале плазмотрона с кольцевым выходным электродом с учетом влияя-ния турбулентности и неравновесности плазмы при нанесении защитных и упрочняющих покрытий на заданную поверхность.

Рассмотрим электрическую дугу, горящую в канале плазмотрона между плоской торцевой поверхностью вольфрамового катода и соосно расположенным с ним ступенчатым цилиндрическим медным анодом (рис. 1). Холодный газ (аргон) расходом G подается в канал по цилиндрическим трубкам и на входе в область катодного узла имеет радиальную и тангенциальную составляющие скорости. Предполагается, что течение осесимметричное, плазма квазинейтральная и описывается двухтемпературной ионизационно-неравновесной моделью, скорость генерации заряженных частиц определяется однократной ударной ионизацией и трехчастичной рекомбинацией, излучение объемное.

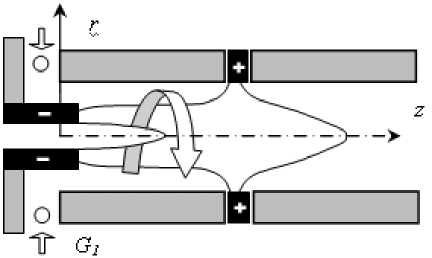
Рис. 1. Расчетная схема плазмотрона: 1 – электроды, 2 – кольцо закрутки

Для описания стационарного течения и нагрева газа применяется система двухжидкостных МГД-уравнений [1], в которых явления турбулентности учитываются эффективными коэффициентами переноса, а пульсации плотности и электродинамические характеристики пренебре-гаются. Уравнения непрерывности, баланса энергии электронов и тяжелых частиц (атомов, ионов), движения, Максвелла и закон Ома записываются в виде:

V (и_еп = h_e + V (Шп_е), V-(^P) = O,

V fjw/1 = ^ ■ VP_e + J • £ + Vi ,1 VT ' +V -1 j^T_e M-n_eU_i - _ГТ_е -T-y,

V -^k_BT^ + и_й ^ = P V(P, + Р_й) + VilVT 1+ pT₆ - Т^+Ж^,

p(y ■ V)P = P+ -pV. P 1+ 2V. (//£) + j x ц_йН ,

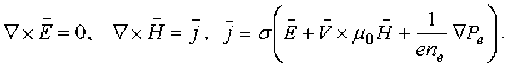
Локальные свойства турбулентного течения описываются кинетической энергией пульсацион-ного движения и скоростью ее диссипации ( k-s модель турбулентности), уравнения переноса которых имеют вид [7]:

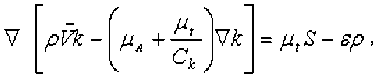
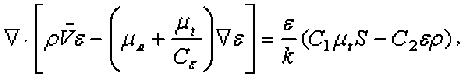
где эмпирические постоянные [8]: С k =1,0, C ε =1,3, C 1 =1,44, C 2 =1,92. Эффективные значения коэффициентов переноса определяются суммой ламинарной и турбулентной составляющих [1]:

^ = ^+^„ Л = ^ +/,г|^, ^ = ^ +^Л£^, D = DQm + ^ ’ Рг,          ’ ^Рг,               р а турбулентная вязкость

Прандтля-Колмогорова, где

–

соотношением

C μ =0,09,   Pr t =0,9.

Система дополняется интегральными условиями сохранения тока дуги и расхода газа, выражениями для диффузионных составляющих плотности электронного тока, скорости генерации заряженных частиц вязкой диссипации энергии

уравнениями состояния, а также зависимостями коэффициентов переноса и теплофизических свойств неравновесной плазмы от температур электронов, тяжелых частиц и давления [1]. Генерация турбулентности в цилиндрической системе координат имеет вид:

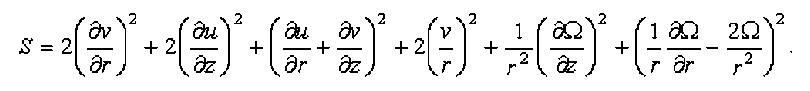
Исходная система уравнений допускает простой переход к ламинарной модели течения, для этого достаточно считать μt=0. В этом случае отпадает необходимость и в решении уравнений турбулентности k, ε. Граничные условия для функций φ=(Te, T, ne, χ, v, u, Ω, Р, k, ε) задаются по замкнутому контуру расчетной области. При решении тепловой задачи для всей среды расчетная область включает электроды, стенки канала, газ и плазму, для электронов – плазму, электромагнитной – электроды и плазму, газодинамической – газ и плазму:

z = 0, 0Т = Т^ ^ = I?kW_k), r>R_K- Т^^Шя; 0 < z < L, r = 0 : v = 0, ^ = 0, 3^/dr=0.

z = L_K, r >0:    3F, / & = 0, ®7_e /3z = 0, v = u = Q= 0, к = 0 ;

z < L, r=J^2; v = u. = Q = 0, ^ = 0: г = Д12+^: T = TR, % = И2л\ z= L . ^ф^ск^ = 0, j = 0, F = Fq .

Для электронов на непроводящих стенках канала используется модель электростатического экранирующего слоя [1], а в области расширения дугового потока задаются на условной границе теплового слоя Т(r * )~330 К:

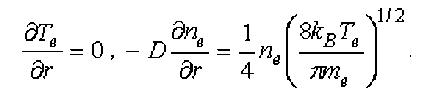
На поверхности электродов для тяжелых частиц используются условия прилипания и непроницаемости, а для электронов – модель адиабатической стенки, приэлектродные процессы не рассматриваются. В области изотермического течения (L k k +L 0 ) составляющие скорости находятся из одномерных уравнений движения с учетом интегральных условий сохранения расхода газа и момента закрутки [10]. На внешних стенках канала температура фиксируется значением T R . При поста-новке граничных условий для диссипации ε на стенке используется масштаб турбулентности l=0,41∙(R-r), а распределения ε и μ t вблизи стенки находятся из выражений [7]:

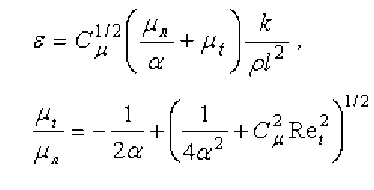
где Re t – турбулентное число Рейнольдса, α=0,4. Сшивка решений ε проводится на границе слоя r=R-δ. Решение уравнения турбулентной энергии ведется до стенок канала, на которых полагается отсутствие турбулентных пульсаций: k=0. Дифференциальные уравнения для переменных φ=(T e , T, n e , χ=rН φ , v, u, Ω, Р, k, ε) приводятся к обобщенной форме и с учетом осевой симметрии записываются в цилиндрической системе координат. Решение уравнений проводится методом конечных разностей в переменных скорость-давление с использованием SIMPLE-процедуры

[14-15]. Построение дискретного аналога обобщенного уравнения осуществляется на неравномерной сетке методом контрольного объема. В дискретных аналогах коэффициенты переноса на гранях контрольных объемов определяются гармонически средним значением, что позволяет учесть скачкообразные изменения свойств среды и достичь достаточно корректной сопряженности на границе раздела фаз. В твердых телах используются теплофизические свойства материала стенки (электрода) с определяющей температурой тяжелых частиц. Для учета нагрева стенки объемным излучением допускается, что энергия излучения поглощается поверхностным слоем контрольных объемов стенки и рассматривается там как локальный источник тепловыделения. Далее эта энергия отводится теплопроводностью вглубь стенки и обратно – в прилегающий к стенке газ. Для удовлетворения условиям сохранности стенки ставится ограничение на расчетную температуру, которая не превышает температуры плавления материала стенки. Такой подход позволяет рассматривать теплофизические процессы одновременно в твердых телах, плазме и газе и применять единую методику решения уравнений во всей расчетной области. На его основе разработан метод расчета характеристик дуги «от катода до анода», который удобен в применении, не требует какой-либо дополнительной информации для задания граничных условий вблизи твердых тел и позволяет сравнительно просто учитывать как форму и мАтериал электродов, так и теплофизические особенности напыляемого материала. Размеры и расположение катодной и анодной привязок дуги, распределения плотности тока и температуры в электродах и плазме устанавливаются в процессе численного решения как результат самосогласованного взаимодействия тепловых, электромагнитных и газодинамических характеристик.

При истечении плазменной струи в канал большего диаметра происходит резкое снижение давления (рис. 2), уменьшаются температура и аксиальная скорость, заметно увеличивается роль турбулентного переноса энергии по сравнению с ламинарным. За уступом канала возрастает радиальная составляющая напряженности электрического поля, линии электрического тока искривляются и замыкаются на поверхность анода. Этому способствует сильная турбулизация потока за уступом канала и большие значения дрейфовых скоростей электронного газа.

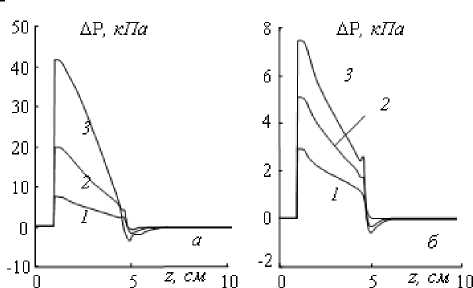
Рис. 2. Влияние расхода газа (а, I=200 А): G=1 (1), 2 (2) 4 (3) г/с и силы тока (б, G=1г/с): I=50 (1), 100 (2) 200(3) А на перепад давления по длине канала

Учет турбулентности газового потока заметно увеличивает термическую неравновес-ность плазмы и напряженность электрического поля, смещает область привязки дуги к аноду по направлению к уступу относительно расчетов по ламинарной модели. Для заданных значений G, I приосевых возвратных течений не образуется, что объясняется сравнительно малыми значениями азимутальной скорости ~ 5 м/с по сравнению с аксиальной ~ 500 м/с. Более заметное влияние на напряжение горения дуги оказывает расход газа, чем сила тока. При I>50 A реализуется возрастающая вольт-амперная характеристика. Следует отметить, что данная методика расчета дуги в приэлектродной области является своего рода компромиссом между кинетическим подходом и МГД-приближением. В ее основе лежат два допущения. Во-первых, влияние приэлект-родных процессов на характеристики дуги атмосферного давления локализуется в узких областях и быстро убывает от поверхности электродов. Во-вторых, МГД-уравнения интегрально учитывают законы сохранения переноса заряда, импульса и энергии. В соответствии с этим при расчете сильноточной дуги атмосферного давления можно в первом приближении не вникать в сложную кинетику приэлектродных процессов, а сшивку решений, полученных в электродах и плазме, осуществлять по упрощенной схеме: электрод-плазма. В методе «сквозного счета» подобная сшивка решений для переменных T, χ и их согласование на границе раздела сред происходит автоматически. Очевидно, что данный подход ограничен в применении и не может быть использован для изучения физики приэлектродных процессов – это задача отдельного исследования.