Моделирование уплотнения почвогрунта в боковых полосах трелевочного волока с учетом изменчивости трассы движения

В статье представлена модель объемного уплотнения почвы трелевочными тракторами, позволяющая прогнозировать степень ее уплотнения в полосах, прилегающих к волокам, с учетом изменчивости трассы движения тракторов. Ключевые слова: трелевка, уплотнение почвы, трасса движения, поворот трактора

Проблема уплотнения почвогрунтов, разрушение их структуры в процессе циклического нагружения массой трелевочного трактора и трелевочной системы (ТС) на его базе, является актуальной. Решению вопросов прогнозирования деформации и уплотнения почвогрунта под воздействием движителей машин и древесины при использовании одномерных моделей о вдавливании штампа посвящены работы [1], [2], [3] и др.

Исследования объемной модели деформирования грунта в главных напряжениях направлены на минимизацию вредного воздействия техники на подрост и его корневую систему при многократном проходе ТС [8], что обусловлено требованием движения по заранее намеченным трассам волоков. Однако в процессе трелевки точно выдержать заданное направление движения не представляется возможным, и трактор вынужден неоднократно совершать поворотные движения. В этом случае грунт находится в объемном напряженно-деформированном состоянии и напряжения возникают на произвольных, в общем случае - неглавных площадках, что обусловливает возникновение дополнительных касательных напряжений в направлении, перпендикулярном действию нормальной нагрузки.

Рассмотрим действие на грунт сосредоточенной силы Q = G + Q 1, где G - сила тяжести трактора, Q 1 - сила тяжести пачки, размещенной на тракторе (рис. 1). Процесс деформирования происходит в пространственной декартовой системе координат Oxyz, оси которой принимаются главными, а на элементарных площадках массива действуют соответствующие главные напряжения а 1 = az, а2 = ay, а3 = ax, тогда как касательные напряжения отсутствуют.

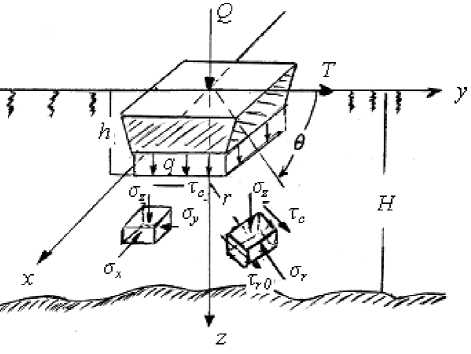
Рис. 1. Схема объемного напряженного состояния грунта при повороте штампа

В процессе погружения грунтозацепа (штампа) на глубину h происходит уплотнение грунта, который испытывает действие вертикальной нагрузки (вертикального давления) q. Поскольку к штампу кроме вертикальной силы Q приложена касательная (горизонтальная) сила Т тяги трактора, возникает деформация грунта в направлении действия этой силы. Следствием этого является формирование горизонтальной нагрузки τс (горизонтального давления), характеризующей величину удельного сопротивления грунта срезу.

В момент маневра трактора и отклонения ТС от заданного направления движения на угол θ деформирование грунта целесообразно рассмотреть в цилиндрической системе координат Ozrθ . Компоненты тензора напряжений в этой системе в общем случае при наличии касательных напряжений τ rθ , совпадающих по направлению с действием нагрузки τ с , определяются соотношениями [4]:

σ + σσ - σ σ = σ ; σ = ²³ + ²³ cos2 θ ; z 1 r 22

σ + σσ - σ        σ - σ

_θ = 2 2 3 - 2 2 3 cos2 θ ; τ r _θ =- 2 2 3 sin2 θ .

Из соотношений (1) следует, в частности, что при θ = 0 компоненты тензора напряжений являются главными, то есть имеем:

σ z = σ1, σr = σ2, σθ = σ3, τrθ = 0, и будут определяться соотношениями [3]:

(2а)

σ = -3Qz3(r2+z2)-5/2, z    2π ar = Q-J (1 - 2v)l — -—(r2 + z2)-1/2 I - 3r2z(r2 + z2 )-5/2 [, (26)

2 п I I r ² r ²                   I                           J ^{v 7}

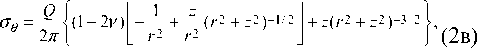
где ν – коэффициент бокового расширения (коэффициент Пуассона).

Из анализа соотношений (2а)–(2в) можно заключить, что если среда абсолютно несжимаема ( ν = 0,5), то уравнения, определяющие напряжения в вязко-упругой среде, трансформируются в уравнения чистой упругости. Применительно к поставленной задаче трелевки лесоматериалов такое состояние почвы характерно для весенних и осенних периодов, когда она чрезмерно увлажнена и глубина ее слоев в таком состоянии достигает 0,5 м [1].

На рис. 2 при исходных данных Q = G + Q 1 = 150 + 40 = 190 кН и ν = 0,35 представлены зависимости величины τ_rθ , кПа, от координаты r , характеризующей величину удаления элемента массива от штампа, м, для трех значений угла поворота θ .

Как видно из рис. 2, для всех трех значений углового параметра θ отрицательный показатель степени в экспоненциальной функции обусловливает достаточно интенсивное снижение касательных напряжений в массиве грунта с ростом величины r, то есть по мере удаления от трассы волока.

Необходимо также отметить, что при r → 0, то есть рассматривая в одномерной постановке процесс деформирования грунта в непосредственной близости от штампа, снижение вертикальных напряжений σ z подчиняется степенному закону и происходит пропорционально величине 1/ z ². В этом случае связь σ_z с величиной нормальной нагрузки q описывается с помощью зависимости [1]:

σ z

q

1 + ( z / aD )^{2 ,}

где a , D – параметры штампа.

Из (3) следует, что при z = 0 σ z = q .

Под действием давления q и погружении штампа на глубину h происходит деформация близлежащего элементарного слоя грунта.

Вертикальную координату z целесообразно ограничить от 0 до H - h , где H – размер зоны распространения деформаций, то есть удаленность твердого недеформируемого основания почвы от свободной поверхности. Тем самым будем использовать подвижную цилиндрическую систему координат с перемещением центра системы (точки О) вглубь массива по мере погружения штампа.

Величина нагрузки q при вдавливании штампа шириной b на глубину h с учетом вертикального давления в боковых полосах, удаленных на расстояние r от направления волока, определена в [8]:

Е Hk ( r , h ) 1 k ϕ R arctg ^H <

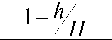
H - h arctg—R— ^

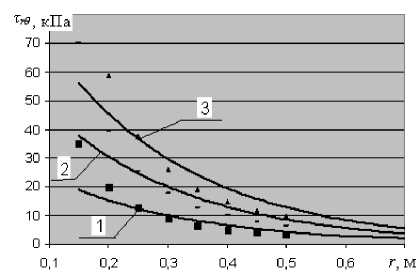
Рис. 2. Изменение величины касательного напряжения по мере удаления от направления волока и роста угла поворота ТС: 1 – θ = 5º ( у = 35,632е^-4,2291х R² = 0,9195); 2 – θ = 10º ( у = 70,992е^-4,2291х R² = 0,9195); 3 – θ = 15º ( у = 105,81е^-4,2291х R² = 0,9195); (здесь и далее R² – коэффициент детерминации)

где Е – модуль деформации,

кф = tg /3

п

ф) 2 )

– коэффициент, учитывающий увеличение общей деформации грунта при погружении ядра

уплотнения, φ – угол внутреннего трения, R = aD - параметр штампа, определяемый через величины a и D :

b

а = 1 +--

Н

D – диаметр круга, равновеликий площади F грунтозацепа, k(r, h) – безразмерная функция, учитывающая снижение напряжений на глубине зоны деформаций h по мере удаления расчетной точки от границы волока.

Величина удельного сопротивления грунта срезу τ с связана с вертикальной нагрузкой q обобщенным уравнением Кулона:

О 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 h, М

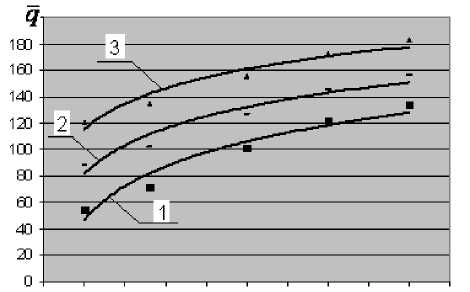
Рис. 4. Зависимости приведенного давления от величины погружения грунтозацепа:

1 – θ = 5º ( у = 28,594Ln(x) + 200,94 R²= 0,9417);

2 – θ = 10º ( у = 31,702Ln(x) + 176,48 R²= 0,9381);

3 – θ = 15º ( у = 36,864Ln(x) + 157,48 R²= 0,9464)

т = qtg ф + C о ,                (5)

где С 0 – внутреннее сцепление грунта.

На рис. 3 при исходных данных Е = 400 кПа, ν = 0,35, С 0 = 12 кПа, φ = 15^о, b = 0,08 м, F = 0,04 м², H = 0,5 м представлены зависимости τ с ( r ) для трех состояний погружения штампа: h = 0,05, 0,13 и 0,25 м. Величина h = 0,13 м соответствует глубине грунтозацепа l d .

Из анализа данных рис. 3 следует, что с ростом глубины погружения грунтозацепа от 0,05 до 0,13 м, то есть на его полную глубину, угловой коэффициент в уравнении прямых, характеризующий интенсивность снижения нагрузки, пропорционально увеличивается по модулю с 4,96 до 12,53. При дальнейшем погружении грунтозацепа пропорциональность не выполняется, что свидетельствует о проявлении нелинейных процессов деформирования грунта под действием вертикальных и соответствующих горизонтальных нагрузок.

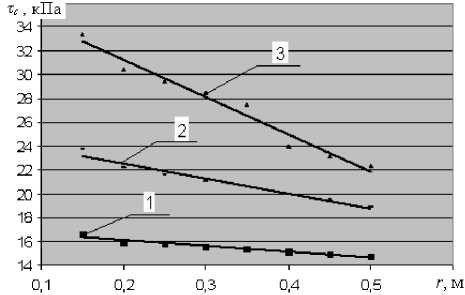
Рис. 3. Зависимость величины горизонтального давления от расстояния удаления от трассы волока:

1 – h = 0,05 ( у = -4,9571 х + 17,129 R²= 0,9616);

2 – h = 0,13 ( у = -12,531 х + 25,006 R²= 0,9612);

3 – h = 0,25 ( у = -31,307 х + 37,521 R²= 0,9674)

Суммируя величину τ с с величиной касательного напряжения τ rθ , получим некоторую результирующую нагрузку τ на грунт, действующую в элементарном слое на глубине h в направлении, перпендикулярном действию нормальной нагрузки q . Тогда величину п р иведенного давления [1] можно определить как q = ^q 2 + т ² .

На рис. 4 для трех значений углового параметра θ = 5, 10 и 15 град. при значении r = 0,05 м (в непосредственной б л изости от волока) представлены зависимости q ( h ).

Процесс уплотнения при циклических нагрузках, когда трелевочный трактор проходит N раз по одному и тому же участку трассы, оценивается с помощью соотношения [2]:

abq (1 -V v pi=1 +           )(i+xign),

EH

где Р 1 - относительная плотность:

Р1=Рр^, р0

ρ₀ = 850 кг/м3 – начальная плотность почвы (плотность влажного почвогрунта естественного сложения), χ – эмпирический коэффициент интенсивности накопления необратимой деформации почвы при повторных нагрузках (в расчетах принят равным 1); ω – эмпирический коэффициент, зависящий от размера и формы опорной поверхности (в расч е тах принят равным 2,15).

Уплотнение р 1 соответствует фазе упругой деформации е 1 = р 1 -1, когда осуществляется процесс активного формирования ядра уплотнения.

Вязкопластическая деформация грунта ε 2 характеризует вторую фазу процесса уплотнения, когда сила сопротивления уплотнению соизмерима с силой сопротивления сдвигу. Величина уплотнения р 2 определяется в соответствии с результатами исследований [7], а соответствующая деформация равна е 2 = р ₂ -1.

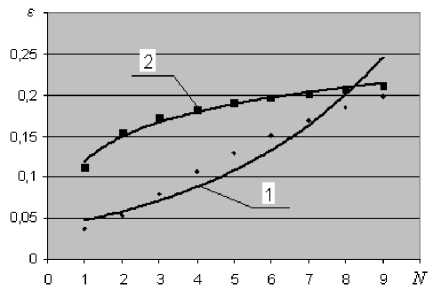
Рис. 5. Изменение деформаций с ростом числа циклов проходки:

1 – упругая деформация, ε 1 ( у = 0,0433Ln(x) + 0,1195 R²= 0,9846);

2 – вязкопластическая деформация, ε 2 ( у = 0,0386е^0,2061х R²= 0,9161)

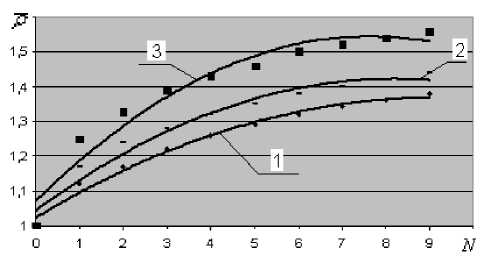
Рис. 6. Зависимости р (N) с учетом изменения угла поворота ТС:

1 – θ = 0 ( у = -0,0081 х ²+ 0,1237 х + 1,0722 R²= 0,9462);

2 – θ = 10 ( у = -0,0056 х ²+ 0,0919 х + 1,0462 R²= 0,9645);

3 – θ = 25 ( у = -0,0041 х ²+ 0,0752 х + 1,0252 R²= 0,9867)

На рис. 5 представлены зависимости ε 1 ( N ) (кривая 1) и ε 2 ( N ) (кривая 2), анализ данных которых показывает, что по достижении определенного числа циклов (для данного примера расчета N = 8) вязкопластическая деформация практически не увеличивается. В механике грунтов [5] этому состоянию соответствует завершение процесса переупаковки грунта, и дальнейшее уплотнение возможно только с развитием упругих деформаций.

Истинная деформация определяется как ε = ε 1 + ε 2 , после чего величину с у ммарного уплотнения можно оценить в виде: р = 8 + 1 .

И з менение величины относительной плотности р от N при погружении грунтозацепа на полную глубину ( h = 0,13 м) для трех значений углового параметра θ = 0, 10 и 25 град. (кривые 1, 2 и 3 соответственно) представлено на рис. 6.

Как видим, по достижении величиной цикличности уровня N = 7–8 графики выходят на свои асимптоты, то есть дальнейшее уплотнение практически не происходит. Можно полагать, что произошли необратимые структурные изменения элементов массива грунта и процесс его упаковки завершен.

Таким образом, результаты выполненных исследований свидетельствуют о том, что величина углового параметра θ , достигая значений 10 и более градусов, оказывает существенное влияние на процесс циклического уплотнения грунта. Данный параметр необходимо учитывать в прогнозных оценках допустимых размеров зон охранных полос, снижающих вредное воздействие ТС на корневую систему подроста и оставляемых на доращивание деревьев при выборочных рубках.