Моделирование упругого поведения многокомпонентных композиционных материалов с использованием приближенных решений стохастических краевых задач
Автор: Ташкинов М.А.
Статья в выпуске: 3, 2015 года.
Бесплатный доступ
Статья посвящена методам статистической механики, их разработке и применению для изучения микроструктурного поведения многокомпонентных композитов. Объектом исследования являются структурно-неоднородные материалы, состоящие их более чем двух компонентов. Целью работы является разработка аналитического инструментария для анализа полей микроструктурных напряжений и деформаций в многокомпонентных средах, позволяющего учитывать геометрические и физико-механические свойства компонентов, на основе вычисления статистических характеристик локальных полей напряжений и деформаций в компонентах. Исследование поведения компонентов микроструктуры композитов основано на концепции представительного объема материалов. Предполагается, что компоненты являются однородными и изотропными. Информация о внутренней морфологии представительных объемов формализуется с помощью моментных функций различных порядков. В качестве характеристик процессов деформирования выступают статистические моменты (статистики) полей напряжений и деформаций в компонентах материала. Аналитические выражения для статистических характеристик локальных полей напряжений и деформаций получены с использованием решения краевой задачи теории упругости в стохастической постановке. Краевая задача решена с помощью метода функций Грина для упругой среды. Разработанная аналитическая модель позволяет учитывать как геометрические параметры микроструктуры, так и физико-механические свойства компонентов. Впервые получены выражения для моментов первого и второго порядка локальных полей напряжений для многокомпонентных материалов. Исследованы частные случаи композитов с титановой (Ti) матрицей, армированных случайно расположенными частицами карбида кремния (SiC). Выполнен анализ влияния микроструктурных параметров на поведение каждой из фаз в отдельности. Представлены численные результаты, полученные для статистик полей напряжений и деформаций.
Моментные функции, случайная микроструктура, статистические характеристики, композиты с металлической матрицей, многокомпонентные представительные объемы, геометрическая модель, локальные поля напряжений и деформаций, стохастическая краевая задача, метод последовательных приближений, теория упругости
Короткий адрес: https://sciup.org/146211569
IDR: 146211569 | УДК: 539.3 | DOI: 10.15593/perm.mech/2015.3.12
Текст научной статьи Моделирование упругого поведения многокомпонентных композиционных материалов с использованием приближенных решений стохастических краевых задач
PNRPU MECHANICS BULLETIN
Появление и широкое распространение новых композиционных материалов связано с необходимостью решения сложных прикладных задач, продиктованных потребностями высокотехнологичных отраслей промышленности, таких как аэрокосмическая, автомобильная, электронная и др. Создание аналитических инструментов, позволяющих предоставить рекомендации для оптимального проектирования композитов, наиболее соответствующих условиям эксплуатации конкретных приложений, является актуальной проблемой. В отдельный класс можно выделить многокомпонентные композиты, состоящие их двух и более фаз, отличающихся по своим исходным свойствам. Развитие подходов к многомасштабному моделированию механической микроструктуры таких материалов дает возможность прогнозирования эффективного поведения композиционного материала с учетом микроструктурных особенностей, таких как размер частиц фаз, их объемная доля, ориентация, дисперсия и кластеризация [1–6].
Метод, используемый в данной работе, основан на статистических подходах и теории случайных функций. Его суть заключается в том, что поведение отдельных компонентов микроструктуры при нагружении представительного объема оценивается с помощью статистических характеристик локальных полей напряжений и деформаций, таких как моменты первого и второго порядка [7–9], которые вычисляются с помощью решения стохастических краевых задач.
Стохастические краевые задачи могут быть сформулированы в реализациях случайной структуры [10] и в моментных функциях [9, 11–13], когда усреднение числа реализаций заменяется усреднением по объему. Решение краевых задач в последнем случае сводится к интегрально-дифференциальному уравнению, содержащему функцию Грина [13]. Уравнение может быть решено различными способами, каждый из которых основан на определенном упрощающем предположении о статистических свойствах материальных характеристик полей композита, что позволяет упростить бесконечную цепочку стохастических уравнений, образованных путем последовательного статистического усреднения определяющих соотношений для компонентов в неоднородных средах [14]. Начало изучению деформирования композитов со случайными структурами в рамках статистического подхода положено фундаментальными работами И.М. Лифшица и Л.Н. Розенцвейга, в которых приведена постановка стохастической краевой задачи теории упругости для поликристаллических сред [15]. Впоследствии этот подход получил развитие в работах В.В. Болотина [15], В.А. Ломакина [12], Т.Д. Шермергора [13], С.Д. Волкова и соавторов [11], Г.А. Ванина [10], а также М. Берана [14], Ю.В. Соколкина, А.А. Ташкинова [9, 17], А.А. Панькова [18], Л.П. Хорошуна [19], Л.А. Сараева [20] и др.
Несмотря на большое количество вариаций статистических подходов, существуют различия в получаемых различными методами результатах для эффективных свойств композитов и в большей мере для статистических характеристик полей напряжений и деформаций в компонентах композитов. Это обусловлено статистической нелинейностью исследуемой задачи и построением приближенных решений, которые в различной степени соответствуют физической модели композита, в частности, его структуре. Отсюда необходимость в получении более точного приближенного решения задачи в рамках существующего подхода, а также обобщения подхода для решения более широкого круга задач.
Данная работа посвящена методологии получения статистических характеристик для многокомпонентных матричных композитов со случайно распределенными включениями на основе решения стохастических краевых задач теории упругости для неоднородных сред.
1. Методология описания характеристик случайной микроструктуры
Внутренняя микроструктура композитов зачастую представляет собой случайную гетерогенную многофазную среду. Согласно статистическому подходу для определения морфологии таких материалов на микромасштабном уровне могут быть введены индикаторные функции X с ( Г) [8, 9, 21, 22]. Значения этих функций зависят от положения радиуса-вектора в представительном объеме. В частности, X с ( r) = 1, если радиус-вектор находится в компоненте C , и X с ( Г) = 0 в других случаях. Тогда тензор модулей упругости для представительного объема определяется как сумма произведений тензора модулей упругости C i ( j z k ) l для каждой компоненты и соответствующих индикаторных функций X (z) ( r) . В результате он принимает форму кусочно-постоянной функции координат:
n
C jki ( r ) = £М Г) C
z = 1
Гипотеза эргодичности случайных функций X с ( г) позволяет рассматривать усреднение по ансамблю реализаций представительных объемов равным усреднению по объему [11, 14]. Другими словами, ^X( z ) ( r )^ = ^X ( z ) (F)^ для каждого r и F - Принимая это во внимание, тензор C ij^l ( F ) и индикаторные функции X с ( r) для представительных объемов можно разложить на два слагаемых – среднее значение и флуктуацию:
C mnk, ( ? ) = ( C mnk, ( F )F C m,„ ( F ) , (2)
X с ( F ) = (X с (r» + X C ( F ), (3)
где флуктуации определяют степень, с которой значение функции отличается от усредненного. Другими словами, они показывают, как случайная структура будет отличаться от периодической структуры с теми же самыми геометрическими параметрами [24]. Усреднение уравнения (1) дает постоянный изотропный тензор, который зависит от объемных долей компонент:
n
{ с» ( F )У 1. p ,z, C jl , (4)
z = 1
где p ( z ) =^X ( z ) ( F )^ - объемная доля фазы z в представительном объеме.
Кроме констант, количественно определяющих структурные геометрические основы, инструменты статистического подхода предлагают механизмы оценки пространственного взаимодействия между микроструктурными компонентами [8]. Так, одним из наиболее широко используемых механизмов являются моментные функции, которые характеризуют связь микрочастиц внутри представительного объема [9, 13, 22]. Таким образом, моментная функция n -го порядка может быть определена как среднее скалярного произведения n случайных величин в различных положениях радиусов-векторов F , F ,..., F .
Выражение для моментной функции n -го порядка флуктуаций случайной индикаторной функции в компоненте C можно записать в общем виде:
где pC – объемная доля.
Моментные функции чувствительны к таким параметрам, как распределение, ориентация и форма микроструктурных составляющих. Теоретически микроструктурная морфология композитов может быть однозначно определена бесконечным числом моментных функций. Эти функции используются в качестве геометрических характеристик в задачах получения статистик высоких порядков для микроскопических полей напряжений и деформаций [8, 9, 13, 16, 22, 24, 27, 28].
Методология моментных функций требует некоторых начальных экспериментальных данных относительно внутренней структуры представительного объема композита. Обычно для получения микроструктурных характеристик используются экспериментальные методы визуализации [23], такие как микрокомпьютерная томография. Другой способ – создание моделей с помощью некоторых заранее определенных геометрических параметров.
Для того чтобы получить значения моментных функций микроструктуры (5), необходимо знать поля значений индикаторных функций (4). Они могут быть вычислены путем выполнения алгоритма, который разбивает представительный объем сеткой с фиксированным шагом и проверяет наличие фаз в каждом ее узле. Точность функций при этом зависит от шага сетки.
В терминах статистического подхода локальные поля, такие как поля перемещений u m , деформаций в у и напряжений ° внутри представительного объема со случайной микроструктурой, как правило, считаются случайными функциями. Они зависят от радиуса-вектора и могут быть представлены аналогично формулам (3) и (4):
um ( r ) = (um ( r )) + um( r ) , Вij(r )ЦВij( r )УВ,у ( r ) , ° д r )=(° д r ^у(r).
Многоточечные статистики, рассчитанные для полей напряжений и деформаций в представительном объеме и в каждой фазе отдельно, могут быть использованы для ана лиза влияния микроструктурных параметров на поведение гетерогенных материалов. Средние (по представительному объему) значения в формулах (6)-(8) являются константами, поэтому статистики строятся для флуктуаций. Распространенные модели для расчета эффективных характеристик материала, как правило, используют моменты локальных полей первого и второго порядка [7, 8]. Моменты первого порядка представляют собой средние значения, в то время как моменты второго порядка также называют дисперсиями. Моменты полей деформаций могут быть определены с использованием флуктуаций перемещений и соотношения Коши:
в у ( r ) =2 ( u ; , , ( r )+ u V i ( r ) )
Флуктуации напряжений можно пред
ставить с учетом уравнения состояния ° у ( г ) = C jkl ( — ) в kl ( — ) в следующем виде:
г\-п'(г\-(п Cr^U (rV (rW (rWb (г}
° ij ( r ) = ° ij ( r ) \° ij / = Cijkl ( r ) \в kl ( r )/ \Cyk l ( r ) в kl ( r )/ + \Cyk l ( r )/ в kl ( r Л (9)
Формулы для моментов первого и второго порядка деформаций и напряжений в компонентах были впервые получены С. Волковым и выражаются через смешанные моменты, объединяющие флуктуации индикаторных функций и локальные поля деформаций [11, 25]:
/ _ \ 1 / t к—\ к—\\
(в,.,) = с„ +-,г-(Сг( r )В;, ( r )), \ y/c ij ^C ( r )P C v i v
1 к —
G,,) =(°а) + r^\"(Cc ( r ) °; ( r )b
\ ij/C \ j/ ^ХC (—)p C V V yv
(Bij (—K p ( — )) C = (B i/ (—K p ( — )) + e y e ap -(в ij^C (Bap ) C +
+
(°у (-K P ( r)) C = (° j ( r Ke ( r)) + (° ij } Kp )-(° ij }c (°сф ) C +
+ x -(. r^ ((^ c ( n° v ( r k3 ( r ^+^ ij } (x c ( r k3 ( r >}+^„e) (^ c ( r к ( - >}).
Численный расчет статистик локальных полей связан с нахождением флуктуаций перемещений, которые могут быть найдены из решения краевой задачи в стохастической постановке [9, 25].
2. Решение стохастической краевой задачи в упругой постановке
Стохастическая краевая задача содержит следующие уравнения:
° ij , j ( r ) = 0,
£ v( r ) = 12 ( u i , j ( r ) + u j , i ( r ) ) ,
° ij ( r ) = C ijki ( r ) e ki ( - ), u i ( Г )| . , = e j r l ’
где (14) - уравнение равновесия; j обозначает частную производную
5/ ■ / dxj ’
(15) - соот-
ношение Коши; (16) - уравнение состояния. Адгезия между компонентами считается идеальной.
Для получения решения для флуктуации перемещений в виде рекуррентного интегрально-дифференциального уравнения был использован метод функций Грина [13, 25]:
а-УЧо Г а g _ ( r , r )
8 x j V a x
8u^1 ( - ) d x,
, 1 n- V
n где x — порядок аппроксимации; Cmnkl (r) = ^X(z)(r)C^nkl. Последовательная процедура, z=1
когда каждое предыдущее приближение подставляется в правую часть, позволяет получить более точные решения [25, 26].
Когда размеры представительного объема много меньше характерных размеров твердого тела, а также в случае изотропного тензора C ^j^nK ( r )^, в качестве функции Грина G m ( r , r 1 ) может быть использован тензор Кельвина-Сомильяны [11, 25]:
у д 6 m k n( r m р m )( r k Р к )
G mk ( r , r1 ) = A I- -I + B _,3
где A и B - константы, зависящие от свойств материала микроструктурных фаз. С использованием первого приближения уравнения (18)
5 u ' (1)( r ) «Л ( z ) c ,- -,r j
------= e kl L C ma-ikl J Gim , j ( r , r 1 ) l X ( z ) ( r 1 ) I dV1
d x j z = 1 V ’ n
флуктуации деформаций из уравнения (7), которые используются в формулах для моментов, выражаются с помощью уравнения (20):
j r) =2 ( uu( r)
+ u jii ( r) ) =2
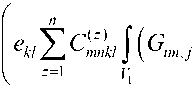
( r , r ) + G jm ,( r , 7X ) )( C ( z ) (D ) 1 dV . (21)
Решение (20) содержит флуктуации индикаторной функций под интегралом. Формулы для моментов (10)-(13) также включают эти флуктуации. Таким образом, в аналитических выражениях выделяются в явном вид структурные моментные функции (5). Например:
/ \ (1)1
(х; , , ( 7 )s j ( r )) = - eH
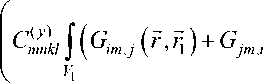
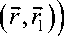
d K^ а^ +
( x1 n
n
Z C mh J ( GmA Г, r ) + G jmA ? , г ) )
Z = 1, z ^ y V
д<Х ( , ) ( r )X ( г ) ( ^
d x 1 n
I dV 1 , 7
гдеK(^r, Г ) = Ck,y ) ( F )X ( y ) ( r)y - моментная функция второго порядка.
Можно показать, что второе слагаемое в выражении (22), содержащее произведение флуктуаций индикаторных функций различных компонент ^X ( у ) ( r )X ( z ) ( 7)c, обращается в ноль. Так, по определению, флуктуация индикаторной функции в компоненте C выражается как
X C ( r) = (X C ( г» -х C ( r ),
где X Cс ( 7)c является константой и отражает объемную долю компоненты в представительном объеме. Тогда осредненное произведение флуктуаций индикаторных функций для двух разных компонент вырождается в константу:
(X( x )( F ) X ( у )( F )} = (( Р ( x ) — X ( x )( F ) )( Р ( у ) — X ( y )( F ) )) = const, (24)
что обращает производную в подынтегральном выражении в уравнении (22) в ноль. Следовательно,
/ \ 11 Г/ хКк(2)(г,F)
x;,,)=;,(r) = - etiCm,>,n'„/(с„Дг,r)+Cj.,(r,r)) 1 уЛ 1 dVV1 .(25)
21 V°
Аналогично
X X ( у ) ( r ) £ ij ( FK p ( F )) = 4 ekle Ф h C mMC Yn Ф h x
V A d3 K <3) ( г , r , r )
x j J ( C m , j -; r , r ) + G jm , i ( 7.r i ) ) ( С ауд ( r , r ) + С ру , а ( 7,7.) ) ( yЛ 1 27 dV 2 dV
V1 V, dX1 n dx2n где
K X C )( 7, r ) = (C C ( r )C C ( r )) - моментная функция второго порядка; K C C^r, r , r ) =
= ^C C ( r )C C ( r )X C ( 72)c — моментная функция третьего порядка.
С учетом равенства (9) смешанные моменты, входящие в выражения для моментов первого и второго порядка полей напряжений в компонентах и содержащие флуктуации полей напряжений, выражаются через флуктуации полей деформаций:
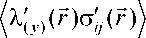
- е D (2)С( y '
= e kl D y ) C ijkl
4^
A p ( y ) p ( z ) C ijkl z = 1, z * y /
-) (, ) ( F )X‘ y ) ( r )E k ( f) C jl+tpy ) ( r H ( f )) ( jw . .
Момент (oj(f)o"ap(r)] равен дисперсии напряжений в представительном объеме как однородной среде:
(°у (fH p ( r ') = e kl e ф h
n
У D(2)^( z )r( z ) A D ( z ) C ijkl C арф h
n
A p(У) p(z) Cijkl CаРФh z=1, z * У
+
nn
+ekl Caарф h A Cijkl (\z) ( r 'Еф h (r ') + eф h CCijkl ) A Cа РФh (X(z)( r 'Еф h ( r ') + z=1
n
+(CWXCw*.) К (г)=Ф/. (r) - «» ACscавФ (ХиХr)x;z)(rA (f)- z=1
nn
-«♦haCsса*h -z)(r:''.'.'r)=k(r)-(C,)ACаahKvf)=;h(04(r))-z=1
nn
-(с-?ф) A Cs K-)( a. (r )=kl ( fy+A CklC«»h (a r^)(?)еф* (r )=kl (fy z =1
где D C 2^ = ^X C ( r ) X C ( r )} = p C (1 - p C ) - центральный момент второго порядка (дисперсия)
для индикаторной функции компоненты C .
В силу свойств индикаторных функций принимать значения, равные либо нулю, либо единице, связь моментов, содержащих произведение индикаторных функций от одного и того же аргумента, выражается следующим образом:
(- C ( r ) - C ( f ) E k, ( f )} = ( 1 - 2 P C )( X C ( f ) E k, ( f )},
(rW (rAr* (rA\-h-^D (2)Wx' f f
(A C ( r ) A C ( r ) A C ( r ) b kl ( ' '/ = ( 1 3 D C )\ A C ( ' ' b kl ( ' '/,
(2) f (
\ - C ( r ) - C ( r ) b kl ( r ) Ьф h ( r )] = (1 2 pC ' (- C ( r ) b kl ( r ) ЬФ h ( r '/ + D C \b kl ( r ) ьф h ( r )/,
(-C (r )XC (r )XC (r )Ek, (rt;h (r >)=(1 - 3 DC21) (XC (r )Ek, (r )6; h (r >)+DC31 (6;, (rt;h (r >), где DCn' =(1 - pC)n pC +(-pC)n (1 - pC) - центральный момент n -го порядка для индикаторной функции компоненты C .
= e kl
Г) (2)С( У )_ y D c( z )
D( y) Cijkl A p (У)p (z) Cijkl z =1, z * y
+ (-I y ) ( f ) = kl ( f )) Ciw'l - ( 1 - 2 p ) C iikl .
k
Для дисперсий напряжений в представительном объеме
(° ij ( r ) ст аР ( r^ = e kl e ф h
V ■ - V „ „ ,уW) L
A D ( z ) C ijkl C аРф h / / p ( y ) p ( z ) C ijkl C аРф h +
У z=1 z=1, z # yу nn
+ekl (CаРфh ) / Cijkl (\z) (r)£фh (r)) + eфh CCijkl ) / Cа₽фh (X(z) (r)£фh (r)) + z=1
n
+ CCijkl ^Cарфh ^ ^kl (r)£фh (r)} - ekl / CijklCаРфh (1 - 2p(z) ) (X(z) (r)£фh (r)) - z=1
nn
-
—ефh A CijklCаРФh (1 — 2p(z) ) (X(z)(r)£kl(r)) - CH^ijkl ^ / C<аРфh (^(z) (r)£фh (r)£kl(r)) -z=1
n
-(C-Sfh) A Cijil '' (Г)£фh (^'ll (r)) + z =1
n
( z )/^( z ) GkAe' С?\с' MkAX-u 12)^ С?\с' CtaW
+ A C ijkl C арф h ( ( 1 2 p ( z ) )\ ^ ( z ) ( r ) £ ф h ( r ) £ kl ( r )/ + D ( z ) \£ ф h ( r ) £ kl ( r )/ ) " z = 1
Аналогичным образом выводится выражение для ^Х C ( г) с'j ( r )с ар (г у .
Полученные аналитические выражения для статистик деформаций и напряжений зависят от свойств материала (через константы, входящие в функцию Грина) и формализованной информации о микроструктурной геометрии (посредством моментных функций различных порядков). Порядок необходимых моментных функций зависит от точности решения (18). С возрастанием его приближения выражения, содержащие интегралы в уравнениях (22) и (23), становятся более громоздкими и включают моментные функции более высокого порядка.
3. Численная реализация методики на примере композитов с металлической матрицей
В качестве частного случая были рассмотрены композиты с металлической матрицей с матрицей из титана (Ti), армированные включениями из карбида кремния (SiC). По сравнению с традиционными материалами и композитами с полимерной матрицей, используемыми для многих прикладных задач, такие композиты проявляют себя лучшим образом при высоких температурах, большую прочность, повышенную устойчивость к износу и высокоцикловой усталости, имеют более высокое отношение жесткости к весу, значительную электрическую и тепловую проводимость.
Микроструктурные составляющие представительного объема композитов были смоделированы как случайно расположенные, непересекающиеся сферы различных размеров. Были рассмотрены три фазы внутри представительного объема: Ti-матрица, армирующие SiC-частицы и пустоты (поры) в разных пропорциях. Такие модели соответствуют данным изображений, полученных из микроструктурных экспериментов, например в [6] и [29].
Геометрические характеристики моделируемых представительных объемов отображены в табл. 1. Поскольку предложенная методика не зависит от масштабных факторов, все величины, характеризующие размеры, представлены в условных масштабных единицах. В качестве представительного объема был рассмотрен куб со стороной 200.
Таблица 1
Геометрические характеристики многокомпонентных представительных объемов
|
Предст. объем |
Объемная доля, p , % |
Количество включений, N |
Минимальный радиус |
Максимальный радиус |
|||
|
Фаза #1 (SiC) |
Фаза #2 (Поры) |
Фаза #1 (SiC) |
Фаза #2 (Поры) |
Фаза #1 (SiC) |
Фаза #2 (Поры) |
||
|
1 |
10 |
1 |
222 |
8 |
8 |
8 |
12 |
|
2 |
15 |
1 |
327 |
8 |
8 |
8 |
12 |
|
3 |
20 |
1 |
445 |
8 |
8 |
8 |
12 |
|
4 |
25 |
1 |
603 |
8 |
8 |
8 |
12 |
|
6 |
10 |
4 |
351 |
8 |
8 |
8 |
12 |
|
7 |
10 |
8 |
511 |
8 |
8 |
8 |
12 |
|
8 |
10 |
12 |
685 |
8 |
8 |
8 |
12 |
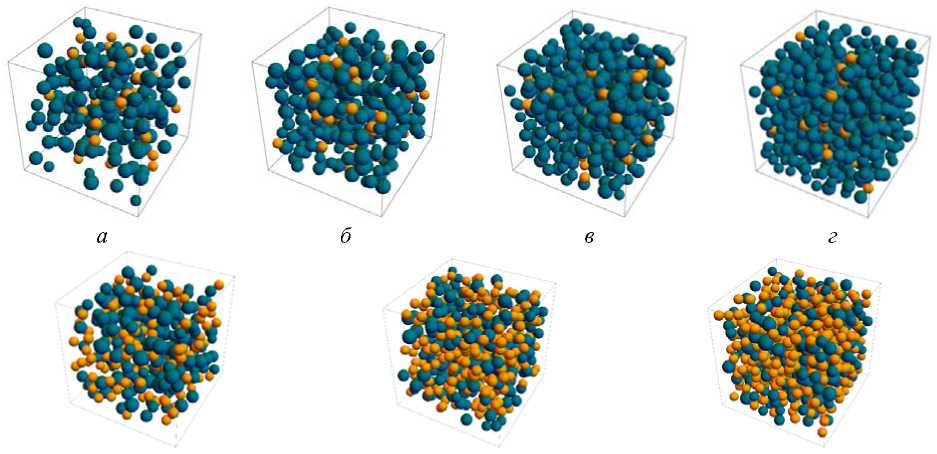
Первые четыре структуры отличаются объемной долей первой фазы (SiC). Структуры 6–8 имеют одинаковую долю SiC-включений, но различные концентрации пор (от 4 до 16 %). Все величины представлены в условных масштабных единицах. 3D-графические изображения этих структур представлены на рис. 1.
д
Рис. 1. Трехкомпонентные представительные объемы материалов с различными объемными долями фаз: а – 10–1 %; б – 15–1 %; в – 20–1 %; г – 25–1 %; д – 10–4 %; е – 10–8 %;
ж – 10–12 %
Заданные механические свойства SiC-включений и Ti-матрицы представлены в табл. 2. Поры считались заполненными вакуумом.
Таблица 2
Механические свойства фаз для случая Ti + SiC-композитов
|
Включения (SiC) |
Матрица (Ti) |
|
|
Упругий модуль |
E C = 410 ГПа |
E M = 116 ГПа |
|
Коэффициент Пуассона |
v C = 0,14 |
v m = 0,32 |
Нагружение представительного объема соответствовало простому сдвигу и было определено путем задания компонент макромасштабного тензора деформаций eij в граничных условиях (17):
e =
V
10 - 6
10 - 6
В случае когда матрица и включения являются упругими, однородными и изотропными, тензор упругих модулей для каждой компоненты является постоянным и может быть представлен в следующем виде:
Cj) = X ’ M н +и'-‘ (Sik 6V, +6„5„),
где X ( - ) , ц ( - ) - постоянные Ламе компоненты - ,
( 1 + v ( - ) )( 1 - 2v ( - ) )’
E ( z )
2 ( 1 + v ( - ) )’
где E ( - ) - упругий модуль; v ( - ) - коэффициент Пуассона.
Коэффициенты A и B функции Грина (19) в случае упругих компонентов связаны с константами Ламе:
A = W + (M B = _W±W_ 8л^ц^Х + 2ц^ 8п^ц^Х + 2ц^
n
n
где W = E X ( - ) Р ( - ) , W = &( - ) Р ( - ) .
- = 1
- = 1
Методология, описанная в п. 1, позволяет вычислять дискретные значения моментных функций, которые не могут быть непосредственно использованы в аналитических выражениях для статистических характеристик. Переход от дискретных значений к непрерывным функциям осуществляется с помощью аппроксимации. Аппроксимация функций может быть проведена путем построения нелинейной аналитической модели со структурой, которая соответствует некоторому заданному выражению для последовательно вычисленных дискретных значений моментных функций. С помощью вычислительных экспериментов ранее было показано [25, 30–32], что степенное выражение с двумя периодическими функциями и тремя независимыми коэффициентами в наибольшей степени подходит для аппроксимации (разница составляет не более 1–1,5 %):
f
K
Здесь A r - расстояние между радиусами-векторами; c i - коэффициенты аппроксимации.
Степень a в соотношении (36) равна 2 для функций второго порядка и 1 – для функций более высоких порядков. Предполагается, что все компоненты являются изотропными, что позволяет принимать все расстояния между радиусами-векторами одинаковыми [24]:
A1 = 11 -'il = 1'1 — 11 = 11 — 11 =... = 11-1 — 1,|. (37)
Для каждого частного случая были вычислены моменты первого и второго порядка полей напряжений и деформаций в компонентах. Подробности об используемых при этом численных методиках содержатся в работах [30, 31].
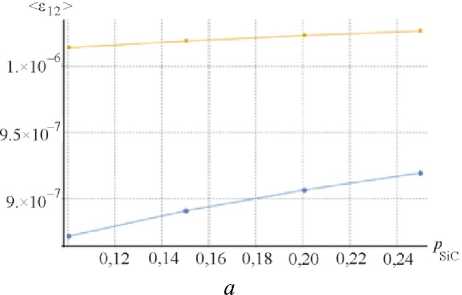
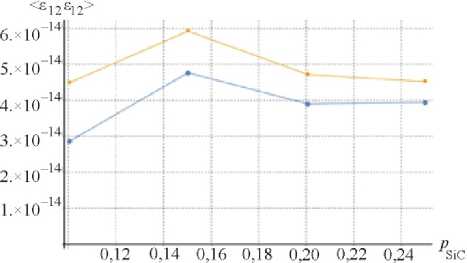
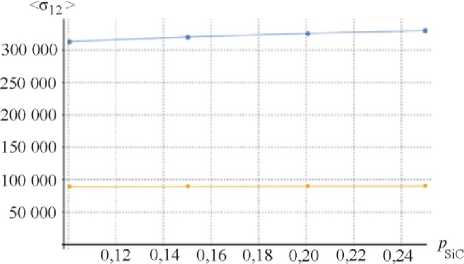
На рис. 2 отображены изменения статистических характеристик как для титановой матрицы, так и для включений в зависимости от объемной доли частиц карбида кремния.
Графики демонстрируют близкую к линейной зависимость для моментов первого порядка – средних значений напряжения и деформации, в то время как дисперсии полей во включениях значительно выше, чем в матрице. С увеличением объемной доли средние деформации как в матрице, так и во включениях непропорционально увеличиваются, что соответствует предсказываемому поведению. Дисперсии напряжений и деформаций в компонентах имеют тенденцию к схождению с увеличением объемной доли армирующих включений.
б
в
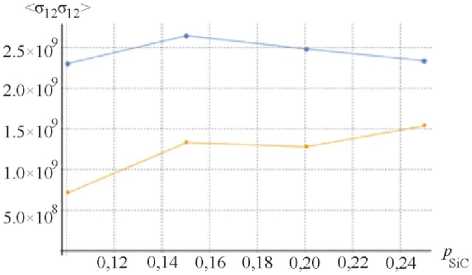
Рис. 2. Значения моментов первого (а, в) и второго (б, г) порядков для представительных объемов Ti+SiC-композитов в зависимости от объемной доли карбида кремния: включения (SiC), матрица (Ti)
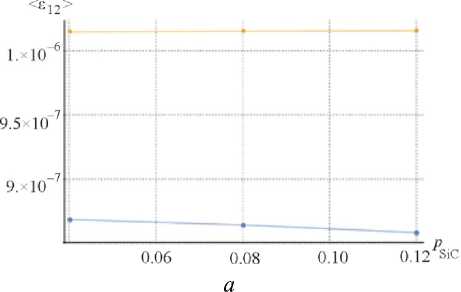
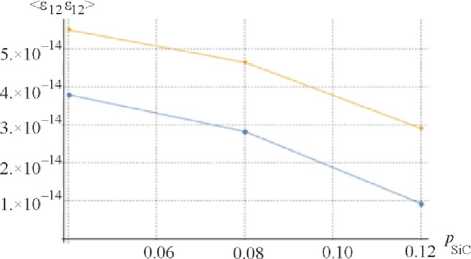
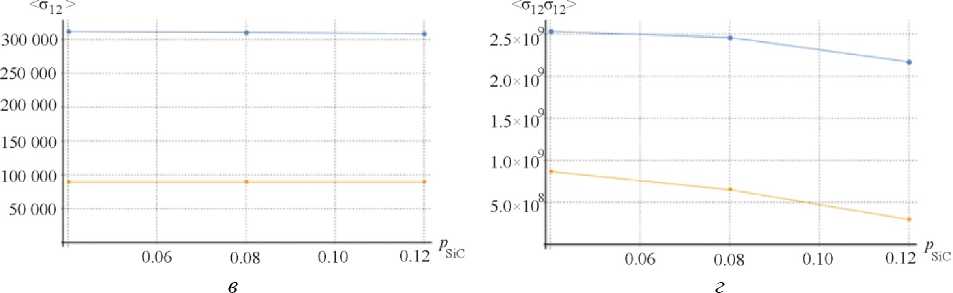
Рис. 3. Моменты первого ( а , в ) и второго ( б , г ) порядков для Ti+SiC-композитов в зависимости от объемной доли пор: -•- включения (SiC), -■- матрица (Ti)
Рис. 3 позволяет проследить влияние микроструктурных дефектов, которые были смоделированы, как поры. Как видно, увеличение пористости практически не оказывает влияния на матрицу. В то же время для статистик первого и второго порядка наблюдаются нелинейные зависимости от объемной доли пор, что свидетельствует о том, что не только количество дефектов, но и их распределение и позиционирование в представительном объеме оказывает влияние на напряжения и деформации в компонентах.
Заключение
Данная работа демонстрирует комплексную методику для получения статистических характеристик полей микроструктурных напряжений и деформаций в многокомпонентных материалах с помощью статистического подхода. Описание геометрии случайной микроструктуры проводилось с использованием методологии моментных функций. Аналитические выражения для статистик были получены с помощью стохастического решения краевой задачи в виде перемещений и учитывают внутреннюю информацию о морфологии посредством моментных функций различных порядков. Точность численных вычислений для статистик с использованием представленной модели может быть улучшена путем использования последовательных приближений решений уравнения (18) более высоких порядков.
Одним из возможных применений для самих статистик локальных микроструктурных полей является создание статистических моделей разрушения в компонентах, где они используются для обнаружения начала разрушения, а также для создания на их основе новых критериев прочности, которые могут адекватно отражать процессы деформации и разрушения.
Исследование возможных вариаций механических и геометрических свойств микроструктуры позволяют оценить их влияние на внутренние поля напряжений и деформаций. Эти результаты могут быть использованы при проектировании новых композитов с предопределенными свойствами и оптимизированной микроструктурой, которые могут быть пригодны для широкой области возможных применений.
Работа выполнена при поддержке гранта Президента Российской Федерации для государственной поддержки молодых российских ученых – кандидатов наук (МК-5172.2015.1).
Список литературы Моделирование упругого поведения многокомпонентных композиционных материалов с использованием приближенных решений стохастических краевых задач
- Liu K.C., Ghoshal А. Validity of random microstructures simulation in fiber-reinforced composite materials//Composites. Part B: Engineering. -2014. -Vol. 57. -Р. 56-70. DOI: DOI: 10.1016/j.compositesb.2013.08.006
- Rasool A., Böhm H.J. Effects of particle shape on the macroscopic and microscopic linear behaviors of particle reinforced composites//International Journal of Engineering Science. -2012. -Vol. 58. -Р. 21-34. DOI: DOI: 10.1016/j.ijengsci.2012.03.022
- Mishnaevsky Jr.L., Derrien K., Baptiste D. Effect of microstructure of particle reinforced composites on the damage evolution: probabilistic and numerical analysis//Composites Science and Technolog. -2004. -Vol. 64. -Iss. 12. -Р. 1805-1818. DOI: DOI: 10.1016/j.compscitech.2004.01.013
- Influence of waviness and curliness of fibres on mechanical properties of composites/A.Y. Matveeva, S.V. Pyrlin, M.M.D. Ramos, H.J. Böhm, F.W.J. van Hattum//Computational Materials Science. -2014. -Vol. 87. -Р. 1-11. DOI: DOI: 10.1016/j.commatsci.2014.01.061
- Yu M., Zhu P., Ma Y. Effects of particle clustering on the tensile properties and failure mechanisms of hollow spheres filled syntactic foams: A numerical investigation by microstructure based modeling//Materials & Design. -2013. -Vol. 47. -Р. 80-89. DOI: DOI: 10.1016/j.matdes.2012.12.004
- Effects of random particle dispersion and size on the indentation behavior of SiC particle reinforced metal matrix composites/R. Ekici, M. Kemal Apalak, M. Yıldırım, F. Nair//Materials & Design. -2010. -Vol. 31. -Iss. 6. -Р. 2818-2833. DOI: DOI: 10.1016/j.matdes.2010.01.001
- Ghossein E., Lévesque M. Homogenization models for predicting local field statistics in ellipsoidal particles reinforced composites: Comparisons and validations//International Journal of Solids and Structures. -2015. -Vol. 58. -Р. 91-105. DOI: DOI: 10.1016/j.ijsolstr.2014.12.021
- Buryachenko V. Micromechanics of heterogeneous materials. -New York: Springer, 2007. -686 p.
- Вильдеман В.Э., Соколкин Ю.В., Ташкинов А.А. Механика неупругого деформирования и разрушения композиционных материалов. -М.: Наука, 1997. -288 с.
- Ванин Г.А. Микромеханика композиционных материалов. -Киев: Наукова думка, 1985. -302 с.
- Волков С.Д., Ставров В.П. Статистическая механика композитных материалов. -Минск: Изд-во Белорус. гос. ун-та, 1978. -208 с.
- Ломакин В.А. Статистические задачи механики твердых деформируемых тел. -М.: Наука, 1970. -139 с.
- Шермергор Т.Д. Теория упругости микронеоднородных сред. -М.: Наука, 1976. -400 с.
- Beran M. J. Statistical continuum theories. -New-York: Wiley. Intersci. Publ., 1968. -493 p.
- Лифшиц И.М., Розенцвейг Л.Н. К теории упругих свойств поликристаллов//Журн. эксперимент. и теорет. физики. -1946. -№ 16. -Вып. 11. -С. 967-980.
- Болотин В.В., Москаленко В.К К расчету макроскопических постоянных сильно изотропных композиционных материалов//Изв. АН СССР. Механика твердого тела. -1967. -№ 3. -С. 106-111.
- Соколкин Ю.В., Ташкинов А.А. Механика деформирования и разрушения структурно-неоднородных тел. -М.: Наука, 1984. -116 с.
- Паньков А.А. Статистическая механика пьезокомпозитов. -Пермь: Изд-во Перм. гос. техн. ун-та, 2009. -480 с.
- Хорошун Л.П. Методы случайных функций в задачах о макроскопических свойствах микронеоднородных сред//Прикл. механика. -1978. -Т. 14. -Вып. 2. -С. 3-17.
- Сараев Л.А., Глущенков В.С. Неупругие свойства многокомпонентных композитов со случайной структурой. -Самара: Изд-во Самар. ун-та, 2004. -163 c.
- Tashkinov M.A., Vildeman V.E., Mikhailova N.V. Method of successive approximations in a stochastic boundary-value problem in the elasticity theory of structurally heterogeneous media//Composites: Mechanics, Computations, Applications. -2011. -Vol. 2. -No. 1. -P. 21-37.
- Torquato S. Random heterogenous materials, microstructure and macroscopic properties. -Springer, 2001. -701 p.
- Lee H., Gillman A.S., Matouš K. Computing overall elastic constants of polydisperse particulate composites from microtomographic data//Journal of the Mechanics and Physics of Solids. -2011. -Vol. 59. -Iss. 9. -P. 1838-1857. DOI: DOI: 10.1016/j.jmps.2011.05.010
- Torquato S. Modeling of physical properties of composite materials//International Journal of Solids and Structures. -2000. -Vol. 37. -P. 411-422.
- Tashkinov M.A. Methods of Stochastic Mechanics for Characterization of Deformation in Randomly Reinforced Composite Materials//Mechanics of Advanced Materials/Eds. V.V. Silberschmidt, V.P. Matveenko. -Springer, 2015. -P. 43-78. DOI: DOI: 10.1007/978-3-319-17118-0_3
- Tashkinov M. Statistical characteristics of structural stochastic stress and strain fields in polydisperse heterogeneous solid media//Computational Materials Science. -2014. -Vol. 94. -P. 44-50. DOI: DOI: 10.1016/j.commatsci.2014.01.050
- Tashkinov M. Probabilistic description of stochastic processes of structural failure in advanced polydisperse composites//Proceedings of 11th. World Congress on Computational Mechanics (WCCM XI)/Eds. Eugenio Oñate, Xavier Oliver and Antonio Huerta. -Barcelona: CIMNE, 2014.
- Tashkinov M., Mikhailova N., Wildemann V. Characterisation of Micro-Scale Mechanical Behaviour of Composites Using Stochastic Boundary Value Problem Solutions//Proceedings of 20th International Conference on Composite Materials. -Copenhagen: Denmark, 2015. -P. 3315-3322, available at: http://iccm20.org/fullpapers/file?f=6OwZadRnYW (accessed 22 August 2015).
- Hybrid composites -Metallic and ceramic reinforcements influence on mechanical and wear behavior/G. Miranda, M. Buciumeanu, S. Madeira, O. Carvalho, D. Soares, F.S. Silva//Composites. Part B: Engineering. -2015. -Vol. 74. -P. 153-165. DOI: DOI: 10.1016/j.compositesb.2015.01.007
- Ташкинов М. Статистические характеристики полей напряжений и деформаций в компонентах композитов со сферическими включениями при различных видах макрооднородного напряженно-деформированного состояния//Решение инженерных задач на высокопроизводительном вычислительном комплексе Пермского национального исследовательского политехнического университета: моногр./под ред. В.Я. Модорского. -Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2014. -C. 172-192.
- Ташкинов М.А. Применение системы WOLFRAM MATHEMATICA для вычисления многомерных интегралов в задачах стохастической механики//Высокопроизводительные параллельные вычисления на кластерных системах (HPC 2014): материалы XIV Междунар. конф. -Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2014. -С. 432-439.
- Ташкинов М.А., Михайлова Н.В. Многоточечные приближения высших порядков в краевой задаче упругости полидисперсных композитов со случайной структурой//Вестник Нижегород. ун-та им. Н.И. Лобачевского. -2011. -№ 4-4. -С. 1799-1800.


