Моделирование условий для расчета энергосиловых параметров асимметричного процесса совмещенной прокатки-прессования

В настоящее время актуальной для металлургических производств является проблема создания модульных технологий производства длинномерной продукции в виде проволоки и профилей из цветных металлов и сплавов. Одним из базовых элементов таких технологий непрерывного производства может стать новый процесс совмещенной прокатки-прессования ¹ . Для данного процесса выполнен комплекс экспериментальных и теоретических исследований, созданы лабораторная и две опытно-промышленные установки на базе прокатных станов. Накопленный опыт, выявленные достоинства и несовершенства конструкций этих установок позволили приступить к проектированию промышленного агрегата, для чего потребовалось выполнить его структурно-параметрическое описание с помощью набора проектных параметров и сформулировать задачи разработки моделей функционирования. Весь комплекс теоретических исследований был ориентирован в основном на моделирование процесса прокатки-прессования с симметричным очагом деформации и не учитывал в полной мере кинематические особенности процесса деформации. В данной статье рассмотрены модели для расчета таких проектных параметров, как силы на валках и матрице, моменты на валках, которые определяют мощность привода в зависимости от скорости вращения валков, требования к силовому каркасу промышленного агрегата, жесткости и прочности конструктивных элементов.

Объектом исследования является процесс совмещенной прокатки-прессования (рис. 1). Процесс осуществляется в закрытом калибре, образованном двумя валками разного катающего диаметра (R1 > R2), перекрытого матрицей в сечении СС'. Валки вращаются с одинаковой частотой, но катающие поверхности калибра имеют разные окружные скорости, в частности vв1 > vв2, а скорость боковых стенок калибра vвк изменяется пропорционально изменению радиуса отR2 до R2к. В качестве исходной заготовки используется непрерывно-литой брус с поперечным сечением h0 • Ъ0, который задается в калибр (сече-ниеЛЛ‘) и подвергается деформации в зоне прокатки до сечения ВВ', затем подвергается распрессовке в зоне до сечения СС' и выдавливанию (прессованию) через матрицу до размера изделия hd с вытяжкой % = (hм • Ъ) / Fизд (Fизд - площадь поперечного сечения изделия). В процессе деформации при различных окружных скоростях валков действует приведенная схема контактных напряже- ний трения Tt (рис.1), причем т1^ т2 в силу различных скоростей скольжения поверхностей валков по заготовке.

Точки приложения равнодействующих сил Р ₁ и Р ₂ в условиях асимметричности процесса деформации располагаются в различных плоскостях, а моменты на валках будут определяться плечом а . каждой силы по отношению к осям валков 0 ₁ и О ₂ . Сила, необходимая для выдавливания Р _пр , создает подпорное давление в остальном очаге деформации. Такой характер действия сил обусловливает особенности построения моделей процесса в зависимости от частоты вращения валков.

Одним из основных факторов, определяющих энергосиловые параметры процесса совмещенной прокатки-прессования, является вытяжка при выдавливании, в связи с чем были выполнены экспериментальные исследования на установке СПП-200 для различных сплавов. На рис. 2,3 представлены зависимости сил на матрице и валках, а также моментов при деформировании в горячем состоянии при температуре 480 °С сплава АД31 в различных калибрах.

Рис. 1. Схема процесса совмещенной пракатки-прессования

Анализ экспериментальных данных показал, что увеличение вытяжки приводит к росту сил на матрице, что свойственно процессу выдавливания, и на валках в связи с ростом давления подпора в очаге деформации от действия силы выдавливания. Установлено что сила на валках всегда больше силы на матрице, что обусловлено большей контактной поверхностью заготовки со стенками калибра, чем с поверхностью матрицы. Уменьшение площади калибра почти в два раза при одной и той же вытяжке приводит к практически такому же снижению сил на матрице и валках при малых вытяжках, а с увеличением вытяжки разность сил в различных калибрах возрастает Последнее обусловлено нелинейным характером прироста контактной площади калибра при увеличении его размеров.

Рис. 2. Зависимость сил на матрице Р _м и валках Р _в от вытяжки X при деформировании сплава АД31: 1 - Р _в , калибр 14 x 22 мм; 2 - Р _м , калибр 14 x 22 мм; 3 - Р _в , калибр 11 x 15 мм; 4 - Р _м , калибр 11 x 15 мм

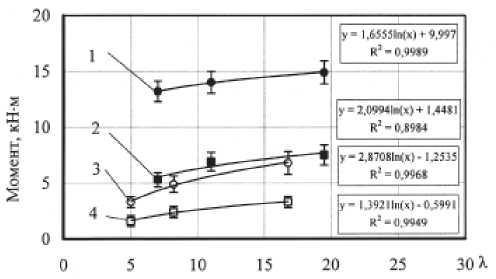
Рис. 3. Зависимость моментов на валках М _] иМ _г от вытяжки X при деформировании сплава АД31: 1 - М ₂ , калибр 14 x 22 мм; 2 - М _] , калибр 14 x 22 мм; 3 - М , , калибр 11 x 15 мм; 4 - М _р калибр 11 x 15 мм

Анализ чувствительности энергосиловых параметров процесса (рис. 4) позволил выявить следующие общие закономерности:

• -    изменение силы на валках чувствительно к изменению силы прессования;

• -    момент на валке с врезом выше момента на валке с выступом практически в 2 раза, что связано с разностью площадей контакта стенок калибра с заготовкой при деформации, а скорость изменения моментов на валках значительно ниже, чем скорость роста силы на валках от силы прессования, что характеризуют значения коэффициентов чувствительности для обрабатываемых металлов, причем более чувствительно изменение моментов к силе выдавливания;

• -    существует корреляционная взаимосвязь между моментами на валке с выступом и валке с врезом.

Для процесса прокатки-прессования, реализуемого на валках разного диаметра, характерны асимметричные условия, что сказывается на геометрических и энергосиловых параметрах. В связи с этим очаг деформации при прокатке-прессовании можно условно разделить на три зоны (см. рис. 1) продольной прокатки -АВВ ‘ А ', распрес-совки - ВСС'В' и прессования - CDD'С'.

На первом этапе рассмотрим зону продольной прокатки, поскольку в зоне распрессовки длина дуг контакта на валках / _{р 1} и / _{р 2} определена удалением матрицы от плоскости О ₁ О ₂ , проходящей через оси валков.

Из условия равновесия заготовки в вертикальной плоскости вертикальные силы равны У2 = У1, тогда можно записать p ср1 б^ж = Р ср2 :\R ^,         (1)

где р _ср - среднее давление; b - ширина калибра; A h ₁ / 2 и A h ₂ / 2 - частные обжатия соответственно со стороны валка с выступом и валка с врезом, причем A h = A h ₁ / 2 + + A h ₂ /2.

Из условия (1) можно записать следующее соотно шение:

A h i _ R   Р ср2

A h ₂

R  Р cpi

R , m ² R ₂

где, учитывая различие контактных давлений на валках 1 и

• ², ™ ^Р Ф1 ^/ Р =р2 .

Для длины зон очага деформации с учетом различных окружных скоростей валков получили следующие зависимости:

i„ _ R 4 v. 2 A&h- , d ¹        v₂\ m²R1 + R2

l d 2

^{_ R}24 "  Г

m ² R 1 R ₂ A h (^) m ² R 1 + R ₂

Для расчета скоростей деформации, необходимых для определения сопротивления деформации металла при горячей обработке, нами получены следующие зависи мости:

_v 2 щ. / RR A h v 2 to₂ m² RR A h 112    212

¹ h 0 mm²R 1 + R ₂ ² h ₀ mm ² R 1 + R ₂

.

Для расчета сил на матрице и валках необходимо учи- тывать температурные условия в очаге пластической деформации. На основании решения уравнения теплопроводности при деформации заготовки в виде бруса и подстановки теплофизических характеристик для алюминиевого сплава АД31 нами получено следующее уравнение:

Т _изд _ Т ₀ + 0,315 ( у и _П р +A Т _П р _ОК +A Т ,„ ) +

+A Тт - 2[ То + 0,315 (A ТпрОк + A Трас ) + A ТТр - Тк ] x где Т0 - температура заготовки,рпр - давление прессования; у - функция критериев Пекле (Ре) и Нуссельта (п), определяемых по следующим зависимостям Ре = v h0/ а, П = /d 1 / h0 и у = П ' Ре / (1 + П:_Ре), причем а - коэффициент температуропроводности, v - средняя скорость перемещения сечений в очаге деформации v = 2R1R2 / (R1 + R2).

Повышение температуры за счет тепловыделения от деформации и трения определяется следующими зависимостями:

- определение среднего контактного давления в зоне распрессовки с учетом давления подпора при выдавли

А Т _прок = - 1,15 о , ln h O- ^, c Р        К

Jh

А Tpac = - 1,155, ln c Р

^А Т ф

= ^T a

2 ( l d i + l p i ) ( - o + b ) h 0 b

вании заготовки;

• -    вычисление общего среднего контактного давления от контактных давлений в зоне прокатки и распрессовки;

• -    корректировка общего среднего контактного давления с учетом его снижения от разности окружных скоростей валков при соответствующей степени деформации.

На основании такого подхода получили среднее дав

ление на валки

Дляусловий: Л ₁ -210мм, Л ₂ -180мм,%-15,1, T 480 °C (сплав АД31), результаты расчета по зависимости (5) представлены на рис. 5. Анализ полученных зависимостей показал:

Р вал

= 5 , ( ^ , T ) 1,15 + 44,15ln ( п ) + 4

Р пр

⁴ 5 , ( ^ , T )

^^^^^^

1,15 -Ь- , (6)

где q - среднее сопротивление деформации в функции от средней скорости деформации и температуры;

• -    с увеличением скорости вращения валков сокращается время теплопередачи между металлом и валками, соответственно уменьшается падение температуры заготовки в зоне прокатки и распрессовки, что приводит к повышению температуры изделия на выходе из матрицы;

• -    увеличение скорости вращения валков снижает влияние разности начальных температуры между валками и металлом на температуру изделия на выходе из матрицы.

Общий подход к построению модели расчета средних контактных напряжений на валках и матрице состоял в следующем:

• -    определение среднего давления в зоне прокатки в калибре с учетом давлений подпора возникающих при осадке заготовки в зоне распрессовки и выдавливании в канал матрицы;

b - ширина калибра; n - h / h ;р - давление выдавлива-^ния р _ПР ⁼ 5 ⁽ ^ ^, ' _ПР ^)(1+1,41п%⁾ •    ^Р

Рассогласование окружных скоростей валков приво

дит к снижению на них средних контактных напряжений,

поэтому предлагается учитывать снижение среднего кон-

тактного давления в зависимости от разности окружных скоростей валков при соответствующей степени деформации следующей зависимостью:

^А Р = Р вал •

,

где v ₁ и v ₂ - окружные скорости валков; е - степень деформации при прокатке, е - А h / h ₀ .

C учетом (7) среднее контактное напряжение на валках будет равно p вал - р - А р , а сила на валках Р - ( р -А р ) ( 1 . 14 i ) ^b .

Сравнение экспериментальных и расчетных данных (рис. 6) показало достаточно высокую сходимость рас-

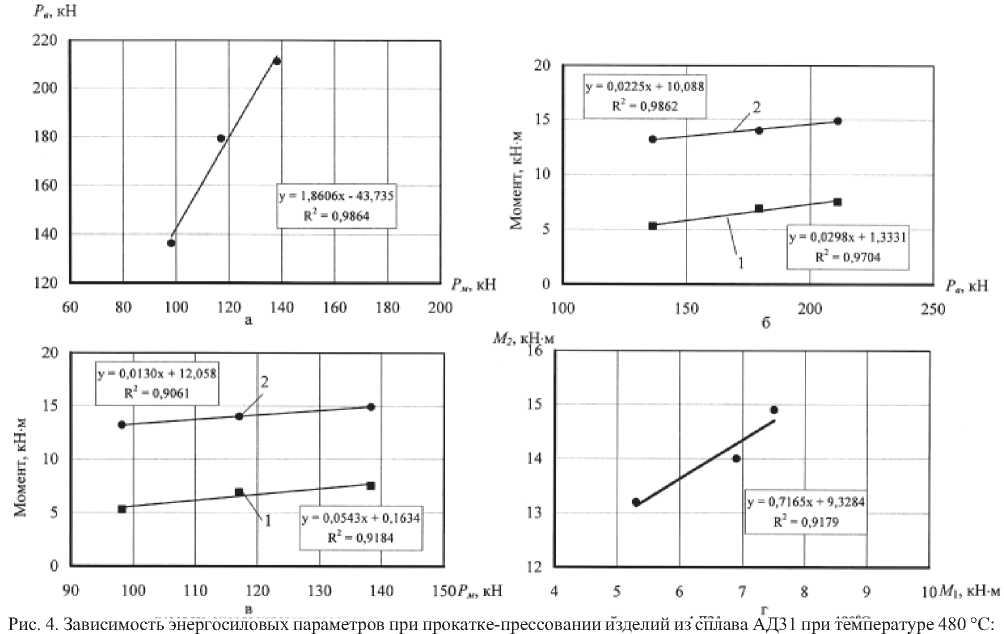
а - силы на валках Р _в от силы на матрице Р _м ; б - крутящих моментов на валках от силы на валках Р _в ; в - крутящих моментов на валках от силы на матрице Р _м ; г - крутящих моментов М , от М ₁ ; 1 - М _х ; 2 - М ,

четных и экспериментальных значений сил на матрице и валках, кроме того, работоспособность и достоверность разработанных моделей подтверждается сохранением закономерностей изменения расчетных данных при изменении экспериментальных параметров вытяжки при выдавливании.

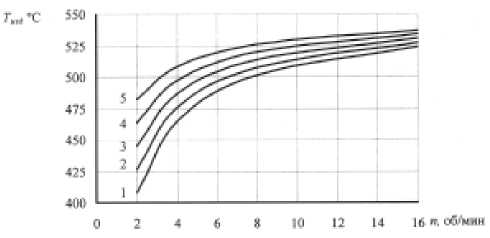
Рис. 5. Расчетная зависимость температуры изделия Г _шд на выходе из матрицы от частоты вращения валов п :

1- Г _в = 150 °C; 2- Г _в = 200 °C; 3- Г _в = 250 °C;

4- Г _в = 300 °C; 5- Г _в = 350 °C

б

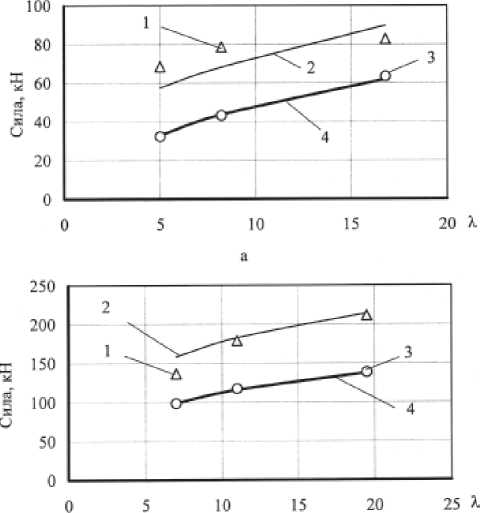
Рис. 6. Зависимость силы на матрице Р _м и валках Р _в от вытяжки X при прессовании на установке CGG-200 сплава

АД31 при температуре заготовки 480 °C:

а - калибр 11 x 15 мм; б - АД31, калибр 14 x 22 мм;

• 1    - сила валках Р _в экспериментальная; 2 - сила на валках Р _в расчетная; 3 - сила на матрице Р _м экспериментальная;

• 4 - сила на матрице Р _м расчетная

Из рис. 1 видно, что равнодействующие Р ₁ и Р ₂ образуют с центрами валков разные по величине плечи а ₁ и а ₂ , поэтому моменты, которые необходимо приложить от привода к каждому валку, будут различны:

• -    для валка с врезом (валок с R ₂ по дну калибра)

М 2 - Р 2 - а 2 - Р 2 R ₂ sin(Y ₂ ±P ₂ );          (8)

• -    для валка с выступом (валок с R ₁ по выступу)

М , - Р ₁ - а ^Р , R ₁ sin(Y ₁ ±e _i ),           (9)

причем знак минус берется тогда, когда точка приложения равнодействующей находится правее линии ВВ ‘ ;

Поскольку ( y ₂ + в ₂ ) > (Y ₁ ⁺ в ₁ ) и Р ₂ >  Р ₁ , то из формул (8) и (9) следует, что М ₂ больше М ₁ , т. е. даже при условии Р ₂ = Р ₁ для привода нижнего валка требуется больший крутящий момент, чем для привода нижнего. Этот вывод подтверждается приведенными ранее экспериментальными данными (см. рис. 2).

Силы Р ₁ и Р ₂ зависят от Р (X), следовательно, М ₁ [ Р ₁ ( Р (1))] и М ₂ [ Р ₂ ( Р (1))] будут возрастать при увеличении вытяжки 1 при выдавливании, что соответствует экспериментальным данным (см. рис. 2).

Исходя из условия равновесия горизонтальных сил можно записать рпр-х1-Х0( откуда следует хрпр-х2,ап

Хрпр"Х1.(

Тогда моменты на валках от горизонтальных сил будут равны

М1 ^-Х1R1,(13)

М2^-Х2R 2,(14)

Моменты от вертикальной силы м1 г-Y1V1 la р(

М2 —2V2 la2,06)

где у ₁ и у ₂ - эмпирические коэффициенты плеча.

На основании анализа экспериментальных данных предлагается использовать для расчета: ^ для алюминия и меди - 0,05.. .0,1, для свинца 0; у ₂ для алюминия и меди -0,5.. .0,6, для свинца 0...0,1.

Сравнение экспериментальных и расчетных данных представлено в таблице. Их анализ показывает достаточно высокую сходимость расчетных значений с экспериментальными, т. е. выполняются закономерности, присущие практическим данным. Следовательно, предложенная модель расчета моментов может быть рекомендована для практического использования в технологических и проектных расчетах.

На основании экспериментальных и теоретических исследований разработаны:

• -    модель геометрии асимметричного очага деформации при прокатке-прессовании, включающая комплекс зависимостей для определения следующих параметров: углов захвата и длины контактных дуг на валках в зависимости от радиусов валков и окружных скоростей их вращения; длины очага деформации; распределения обжатий под валками; коэффициента формы очага деформации под каждым валком и средний для очага деформации; площадей контактных поверхностей;

• -    модель расчета средних давлений на валки при прокатке-прессовании, учитывающая подпор от давления прессования и снижение давлений на валках при сочетании разности их окружных скоростей вращения со степенью деформации. Показано, что в условиях совмещенной прокатки-прессования правомерно применение расчета средних давлений по средним геометрическим размерам асимметричного очага деформации;

  - модель расчета температурных условий процесса     - модель расчета моментов на валках при совмещен-

• СПП с учетом двумерного теплового потока в калибре;   ной прокатке-прессовании.

Сравнение экспериментальных и расчетных энергосиловых параметров при прокатке-прессовании на установке СПП200

Размеры изделия, мм	Материал	Поперечное сечение заготовки h о x b о , мм 2	Сечение калибра hxb , мм 2	Коэффициент вытяжки при прессовании X	Т ian О С	Моменты, кН ■ м
						М t (эксп)	М t (расч)	А М t %	М 2 (эксп)	М 2 (расч)	А М 2 %
0 4	Pb + 2 % Sb	22 x 22	14 x 22	43,8	20	2,80	2,89	-3,11	5,90	5,46	7,48
0 6	Pb + 2 % Sb	22 x 22	14 x 22	19,5	20	3,50	3,31	5,54	6,10	6,02	1,23
0 8	Pb + 2 % Sb	22 x 22	14 x 22	11,0	20	4,00	3,82	4,63	6,40	6,19	3,25
0 6	АД31	20 x 20	14 x 22	19,5	480	5,30	6,24	-17,72	13,20	12,53	5,07
0 8	АД31	20 x 20	14 x 22	11,0	480	6,90	6,82	1,12	14,00	13,46	3,85
0 10	АД31	20 x 20	14 x 22	7,0	480	7,50	7,60	-1,32	14,90	14,80	0,70
0 5	АД31	14 x 14	11 x 15	16,8	480	1,60	1,65	-2,87	3,30	3,29	0,38
0 7	АД31	14 x 14	11 x 15	8,2	480	2,40	2,43	-1,13	4,90	4,58	6,55
0 9	АД31	14 x 14	11 x 15	5,0	480	3,30	3,26	1,12	6,80	6,32	7,04
0 8	А7	20 x 20	13 x 22	11,0	470	4,90	4,89	0,14	6,50	6,50	-0,06
0 9,5	А7	20 x 20	13 x 22	7,8	470	5,30	5,22	1,53	7,20	7,16	0,59
0 11	А7	20 x 20	13 x 22	5,8	470	5,80	5,54	4,48	8,00	7,82	2,28
0 5	А7	14 x 14	11 x 15	16,8	470	1,30	1,40	-7,92	3,00	2,85	5,07
0 7	А7	14 x 14	11 x 15	8,2	470	1,60	1,56	2,63	3,40	3,30	2,96
0 9	А7	14 x 14	11 x 15	5,0	470	2,20	2,19	0,45	4,60	4,52	1,82

I. N. Dovzhenko, N. N. Dovzhenko, S. В. Sidelnikov

MODELING WAYS FOR CALCULATING ENERGY-POWER PARAMETERS ASYMMETRICAL PROCESS OF THE INTEGRATED ROLLING-PRESSING

Different models of calculating energy-power parameters of the integrated rolling-pressing are examined in the present article. The integrated rolling-pressing is a new way for modular processing production. It is used in a sphere of gross metal production from nonferrous metals and alloys. Comparative analysis of modeling results and experimental data are shown in the present article.