Моделирование условий эксплуатации и уточненный прочностной анализ уплотнительных элементов из терморасширенного графита

Терморасширенный графит (ТРГ) - уникальный материал, который вне зависимости от условий эксплуатации (повышенные температуры, термоциклирование, время контакта с агрессивными средами) обладает высокой термохимической стойкостью, низким коэффициентом трения, высокими упругими свойствами. Уплотнительные элементы из ТРГ (УЭ) надежны и не требуют дополнительной герметизации при эксплуатации, работают при температурах от криогенных до 560 °C и давлениях до 40,0 МПа [2-4]. В настоящее время происходит интенсивное внедрение УЭ на предприятиях и промышленных объектах аэрокосмического, металлургического, нефтегазового и химического комплексов, на предприятиях энергетики и ЖКХ [3]. Традиционные способы отработки УЭ (на натурных конструкциях и опытных образцах) не оправдали себя вследствие высокого риска возникновения аварий, сопровождающихся серьезным экологическим и экономическим ущербом. Поэтому большое значение приобретают методы мате- матического моделирования поведения ТРГ, с помощью которых можно прогнозировать теплофизико-механические свойства этого материала, описывать поведение, проектировать новые УЭ и пакеты УЭ, оптимально соответствующие условиям нагружения конкретного узла или агрегата [5].

Будем рассматривать кольцевые УЭ и пакеты из двух одинаковых УЭ, каждый из которых является толстостенным, ограниченным по высоте h , однородным трансверсально-изотропным цилиндром с осью симметрии бесконечного порядка z (0 <  z <  h ), совпадающей с образующей. Поперечные сечения цилиндров ограничены двумя концентрическими окружностями с радиусами а и b ( a <  b ).

При построении модели термомеханического поведения УЭ (или пакета УЭ) будем предполагать, что ТРГ является линейно-упругим материалом, внешнее термосиловое воздействие на который приводит к бесконечно малому изменению объема и формы физических точек. Краевая задача состоит из уравнений равновесия

6с rr +15с r е ! dozr ! ст rr -Gee = 0  6с r е +1 6сее , 6сzе + 2 Gro

6r   r бе    6z       r ’ 6r   r 6е    6zr ’

6g zr +16сеz /^z + ^zr = 0 6r   r 6е    6zr в отсутствие массовых сил и геометрических соотношений Коши

6 u_r ^r

° rr          ’

6 r

1 6 и_г

—- + и

— —           I

°^ее    r 6е

r

, ° _zz

6 и         1 (6 и,   6и, |

---- , ° _zr = -I ---- +   I

6 z        2 у 6 r   6 z J

1 1 (6 u,

° ^{r е} 2 r l 6е

r

I 6 u_fi u_A +—^{е е}) 6 r

° е z = 2

6 uA 1 ( 6 u е + z

6 z r l 6е

записанных в цилиндрических ортогональных координатах r , е и z , а также определяющих соотношений

СТ rr = K 11 ° rr ⁺ K !2 ° ее ⁺ K 13 ° zz Р rr T ’ ^с ее = K 12 ° rr ⁺ K 11 ° ее ⁺ K 13 ° zz ^- Р ее T ,

Gzz = K13 (°rr +°ее) + K33°zz - pzzT, Grе = G°rе, Gzr = G°zr, сеz = G°еz, содержащих следующие множители:

ˆ

K11 = 3(1 - V2), K12 = D(v - V2), K,3 = VD(1 + v), K33 = D(1 - v2), рrr = Pee = а(K1, + K,2)+ аK13, рzz = 2аK13 + аKзз, а также уравнения Лапласа х а < а т) 1 а2 т I г— 1 + га г I а г) г ае2

1 а ² т _ а ^+х— = 0,

аz которое описывает стационарное распределение температур T при отсутствии внутренних источников (стоков) теплоты. Здесь D = (1 + v)(1 -V-2V2), Е и Е, X и X, а и (С - модули Юнга, коэффициенты теплопроводности и линейного термического расширения в плоскости изотропии ге и направлении образующей z ; G и G, -поперечный и продольный модули сдвига, v и 'V - коэффициенты Пуассона.

Решение краевой задачи (1)-(4) будем искать численно методом конечных элементов.

Будем считать, что на внутренней и внешней боковых поверхностях УЭ и пакета УЭ Г1 и Г2 (рис. 1) заданы постоянные температуры высокоагрессивных и реакционно-способных газов или жидкостей Tint и окружающей среды Text:

T

= т . т\ =т .

int ’ Г 2 ext .

Г 1

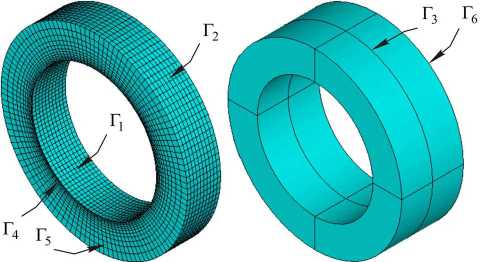
Рис. 1. Дискретизация и схема участков поверхности пакета УЭ

Внешняя боковая поверхность Г ₂ (см. рис. 1) соприкасается с внутренней поверхностью сальниковой камеры так, что исключаются радиальные, осевые и окружные перемещения:

^иА Г ₂ = u е|г ₂ = u z\ Г ₂ = °.                           ⁽⁵⁾

На участке Г ₆ отдельного УЭ или пакета, контактирующем с нажимной втулкой, задано в направлении образующей торцевое давление герметизации, однородность которого обеспечивается прижимными болтами, и отсутствуют касательные напряжения

° zz | г ₆ = - Р^ ’ ° r е| Г ₆ = ° z е| Г ₆ = ° •                   ⁽⁶⁾

На участке Г ₄ торцевой поверхности, ограниченном двумя концентрическими окружностями с радиусами а и d ( a <  d ), задано создаваемое рабочими средами однородное давление

_ I        „ work

°zz \ Г4     pzz , а на участке Г5 той же поверхности, но ограниченном окружностями с радиусами d и b (d < b), исключены перемещения ur, uz и ие:

u r l Г ₅ = u е Г = u z l Г ₅ = °.

Точки, принадлежащие участкам торцевых поверхностей Г ₆, Г ₄ и Г ₅, закрепляются так, что оказываются не способными свободно перемещаться в своей плоскости:

u lr г г = U elr г г = °.

r ¹ 1 3 , 1 4 , 1 5          ^е1 1 3 , 1 4 , 1 5

Предполагая движение штока возвратно-поступательным, зададим однородное распределение осевых перемещений uzl Г1 =±uZnt

на внутренней боковой поверхности Г1. На участке Г3 поверхности контакта колец, входящих в пакет, предполагается равенство темпера тур и тепловых потоков:

V Г

Г з

=[ T ]

5 T

,

Г з

5 z

Г з

5 z

Г 3

а также идеальное сопряжение

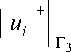
= [ ut\

, ^[ ( ^G rr ^{+ G} rz ^{+ G} r _е ) n r ^]+

Г з

Г з

= ^[ ( ^G rr ^{+ G} rz ^{+ G} r е ) n r ^]

Г з

или проскальзывание urnrl г3 = 0, Grel г3 = Gzel г3 = 01

Будем рассматривать начальный режим работы изготавливаемых крупносерийными партиями УЭ (используются в кранах с уплотнениями по штоку), внутренний, внешний радиусы и высота которых равны соответственно: a = 15,0 мм, b = 22,5 мм, а H = 8,0 мм. При численном решении термоупругих задач в трехмерной постановке методом конечных элементов с использованием пакета ANSYS 12,0 температуры рабочей и окружающей сред принимались равными соответственно T int = 300 °C, T int = 550 °C и T ext = 20 °C. Рабочее давление и торцевое давление герметизации на поверхности контакта с нажимной втулкой p ".^ork = 40,0 МПа и p zZ°^nt = 2 p z W ^ork соответственно. Упругие и теплофизические постоянные ТРГ выбрались следующими: E = 9,04 ГПа, E = 0,75 ГПа, v = 0,03, V = 0,05 , G = 0,47 ГПа и G = 0,35 ГПа [6]; 2 = 122,0 Вт/ ( м • К ) и 2 = 87,0 Вт/ ( м • К ) при T int = 300 °C, 2 = 90,0 Вт/ ( м • К ) и X = 70,0 Вт/ ( м • К ) при T int = 550°C [7, 8]; а = 1,21 • 10 ⁶ К ¹ и а = 2,77 • 10 6 К " 1 .

Максимальные по абсолютной величине значения инвариантов тензора напряжений (МПа) в пакетах УЭ из наноструктурированного ТРГ при возвратно-поступательном движении штока

T int,	Движение в сторону нажимной втулки				Движение от нажимной втулки
ºC	j ( ! ) G	j 2 G	j 3 G	j ( 4 ) G	j ( 1 ) G	; ( 2 ) j G	j 3 G	j ( 4 ) G
300	6,3	57,4	10,5	73,6	6,5	57,6	10,7	66,1
550	7,2	57,4	12,1	80,5	7,3	57,6	12,3	72,8
Идеальное сопряжение УЭ в пакете					Скольжение на поверхности контакта УЭ в пакете
300	6,7	57,3	12,2	76,3	7,2	57,1	14,3	78,5

Были разработаны и программно реализованы комплексы определения значений независимых инвариантов тензоров напряжений [10]

7? = 2 (° rr + °ееЬ j°2С =° zz, j°3С = (°rr -°ееС2 + 4°2е 1 ,                       (8)

• (4) Г 2 , 2 I12 j° -|_°rz + °еz J относительно ортогональных преобразований, допустимых над цилиндрически трансверсально-изотропным телом с осью симметрии бесконечного порядка. Вычисление этих величин в пакете ANSYS 12.0 не предусмотрено.

Результаты, представленные в таблице, показывают, что наиболее чувствительными к изменению температуры рабочей среды T int являются первый, третий и четвертый инварианты. Кроме того, изменение условий на поверхности контакта УЭ из наноструктурированного ТРГ с идеального сопряжения на скольжение при одной и той же T int приводит к увеличению максимальных по абсолютной величине значений j °^c , j °⁴ и j ° ⁴, а также снижению j ° ². Обратим внимание на то, что ни одно из приведенных в таблице значений не превосходит критическое j 173,3 МПа, j (²t = 138,4 МПа, j (⁴ = 138,8 МПа и

О cr                            ° cr                            ° cr jсо- = 84,2 МПа (эти величины вычислены по экспериментально определенным прочностным постоянным на сжатие и сдвиг в плоскости изотропии: S- = 173,3 МПа и Tmax = 69,4 МПа; на сжатие в осевом направлении S- = 138,4 МПа и на продольный сдвиг Tmax = 59,5 МПа).

Анализ факторов, существенно влияющих на характер распределения независимых инвариантов (8) в точках поперечных сечений УЭ, входящих в пакет (толщина, количество колец в сальниковой камере), позволит провести оценку влияния механизмов разрушения на начальную прочность и сравнение различных режимов возвратнопоступательного движения штока (движение в сторону нажимной втулки и в противоположном направлении).

На рис. 2 представлены распределения третьего и четвертого инвариантов тензора напряжений в уплотнительном кольце из нано-структурированного ТРГ при движении штока в сторону нажимной втулки. Несмотря на то, что максимальные касательные напряжения наблюдаются вблизи поверхности Г1 УЭ, контактирующей со штоком, наибольшие значения j(3) имеют место на внешней боковой ,                                            о поверхности Г2, а jO - еще и на участке, контактирующем с на жимной втулкой Г6.

Г б

■ ( 3 ) j о ^,

МПа

0,08

0,30

0,52

0,74

0,96

1,18

1,40

1,62

1,81

2,06

■ ( ⁴ ) j о ^, 0,98

1,92

2,68

3,16

3,80

4,74

5,68

6,62

7,56

8,50

МПа

Г б

а

б

Рис. 2. Распределение третьих j 0 ^{3 )} ( а ) и четвертых j 0 ^{4 )} ( б ) инвариантов тензора напряжений в уплотнительных кольцах из наноструктурированного ТГР при T int = 550 °C

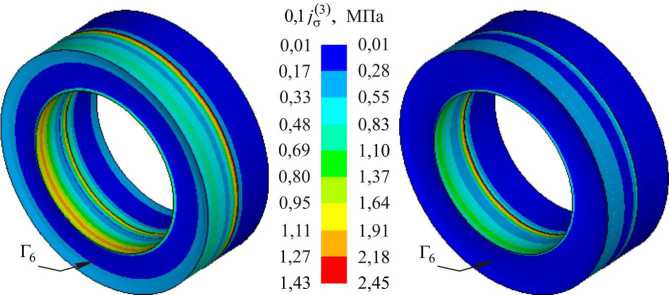
На рис. 3 представлены распределения третьего инварианта тензора напряжений в пакете из двух УЭ при температуре рабочей среды T int = 300 °C. На границе контакта колец Г ₃ были заданы условия проскальзывания. Как видим, наибольшие значения j 0 ^{3 )} имеют место на внешней и внутренней боковых поверхностях в областях, примыкающих к нажимной втулке и границе контакта колец в пакете. Поэтому слабое сопротивление ТРГ сдвиговому воздействию в плоскости изотропии является основной причиной, наблюдаемой при эксплуатации кранов с уплотнением по штоку потери герметизации и разрушения на отмеченных участках.

а

б

Рис. 3. Распределение третьих инвариантов тензора напряжений в пакете УЭ при возвратно-поступательном движении штока: от нажимной втулки ( а ) в сторону нажимной втулки ( б)

Обратим внимание на еще одну закономерность распределения инвариантов тензора напряжений в УЭ и пакетов УЭ. Результаты, представленные на рис. 3, свидетельствуют о зависимости четвертых инвариантов от направления движения штока. Для объяснения последнего эффекта получим аналитические выражения для компонент тензора напряжений в точках УЭ. Будем предполагать, что шток (ось симметрии которого совпадает с осью симметрии УЭ) совершает возвратно-поступательное движение в направлении образующей. Будем пренебрегать вкладом температуры в напряженное состояние, а также окружными перемещениями. Отсутствие вращения штока будет предопределять отсутствие зависимости радиальных и осевых перемещений ( u r и u_z ), радиальных ( ст _rr и a _rr ), окружных ( ст_ее и £_ее ), осевых

(стzz и azz) нормальных напряжений и деформаций, касательных на пряжений и сдвиговых деформаций (стrz и £rz ) от окружной координа ты е. Поэтому геометрические соотношения (2) значительно упро стятся и запишутся следующим образом:

S u_r        u_r        S u₇

^£ rr = ^r , ^£ее = — , ^£ zz = ^z , ^£ rz о r        r         S z

• 1    ^S u z ! ^Sur

• 2    S r    S z

.

Будем рассматривать режим «приработки» сальникового уплотнения, когда арматура собрана и герметизирована нажимной втулкой, передающей на торцевую поверхность кольца Г ₆ равномерное давление. Тогда первое условие (6) можно представить в виде

°z ( z 1-H

front ^p

Принимая справедливыми условия (5) отсутствия радиальных и осевых перемещений на внешней ( r = b ) боковой поверхности Г ₂ и условия (7), моделирующие перемещение точек внутренней ( r = a ) боковой поверхности Г 1 УЭ вместе со штоком, а также предполагая, что осевое перемещение однородно вдоль координаты z , т.е. u _z = u_z ( r ) , запишем уравнения равновесия в виде

^A 11

б ² u_r б r ²

^^

+ G

бz г б 2 ur

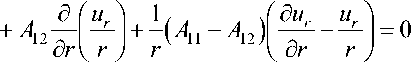
G

б ( б и б и ) 1 ( б и б и ) —I —-+—- I+-I —- + —- I б r v бz б r ) r v бz б r )

. б (б и    и ) _

+ A 13 —I —- + — 1 = 0.

б z V б r    r )

Последние уравнения получены в результате последовательной подстановки геометрических соотношений (9) в определяющие (3) и уравнения равновесия (1).

Решение системы (11) будем искать методом разделения переменных, предполагая и ( r, z ) = Z ( z ) R (r ).

Тогда условие на верхней границе УЭ (10) в перемещениях запишем как

Z (H)

бR (r) R (r)

б r      r

front p_zz

^A 13

и найдем общий вид одной из неизвестных функций, входящих в (12),

R(г)

r 1

С, — + Сз

12    2

. r

Заметим, что во второе уравнение системы (11) входят смешанная и первая производная радиальных перемещений по осевой координате. Однако это уравнение должно быть разрешено относительно радиальной координаты ввиду того, что u_z = u_z ( r ) . Поэтому смешанная и первая производная радиальных перемещений по осевой координате не должны зависеть от z . Это накладывает ограничение на вид второй неизвестной функции в (12)

Z ( z ) = c₃ z - c 4 .

Подстановка (12) в первое уравнение (11) приводит к выражению c3

r 1 In cl- + c 2- 1 = 0.

2 r 7

Равенство нулю множителя, стоящего в круглых скобках формулы (13), автоматически приводит к тривиальному решению u_r ( r , z ) = 0 , которое соответствует естественному ненапряженному стоянию УЭ до помещения его в сальниковую камеру и до герметизации. Поэтому для исключения этого частного случая полагаем c ₃ = 0 и, как следствие, делаем вывод о независимости радиальных перемещений от осевой координаты:

r 1

u r = u r ( r ) = c 1 2 + c 2 r •

Подстановка (14) во второе уравнение (11) преобразует последнее к форме б 2 и   1 б и

—f +--z- = 0, б r2 r б r доступной для интегрирования. Константы интегрирования частного решения

uz (r) = c5 + c6ln r находим из условий (10), (5) и (7) на внутренней, внешней и торцевой поверхности, контактирующей с нажимной втулкой. Тогда распределение осевых и радиальных перемещений будет описываться соотно шениями int u_ = ± u„ zz

ln r - ln b

1 -v-2v

² f b ² I

ln a - In b ’ u^r 2 E v ( v-v ² ) ( r

r p.

front zz ^,

а касательное, осевое, радиальное и окружное напряжения в поперечных сечениях УК определятся следующими выражениями:

а

rz

int 1 G

= + uz--

2 r ln a - In b

^а zz

front

^- Pzz

front zz

2v(1 + v)(v-v2)

b ²

(v -1) — + 2v2 -1 -v

^ ee

zz

2v(1 + v)(v-v2)

b ²

(1 - v) — + 2v2 -1 - v

Как видим, даже в рассмотренном простейшем случае, допускающем аналитическое решение, значения касательных напряжений определяются направлением движения штока.

Разработанная математическая модель УЭ и пакетов УЭ позволяет решить ряд важных задач по определению оптимальных давлений герметизации, обоснованию рекомендаций по внесению изменений в существующие конструкции пакетов УЭ, а также позволяет разработать основы для создания методик уточненного прочностного анализа для инженеров-конструкторов, учитывающих анизотропию теплофизических, деформационных и прочностных свойств ТРГ и различные механизмы разрушения этого материала. Неожиданный результат - зависимость значений инвариантов от направления движения штока был объяснен на основе анализа полученного аналитического решения задачи о деформировании ограниченного по высоте трансверсально-изотропного кольца, на внутренней поверхности которого заданы однородные осевые перемещения, моделирующие первые циклы работы штока в запорной арматуре.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ-Урал № 11-01-96033).