Моделирование условий возбуждения апертурной случайной антенны

Направленные свойства АСА в виде прямоугольного отверстия в проводящем экране исследованы методом СИМ в [1-5]. Условия возбуждения АСА моделируются по аналогии с [6-7] путем решения соответствующих внутренних задач статистической теории антенн (СТА), связанных с определением законов распределения случайных факторов, влияющих на ее эффективность в раз-

Рис. 1. Расположение АСА в декартовой системе глобальных координат и схема лабораторного эксперимента

ных режимах функционирования (амплитудных, фазовых, частотных, временных и геометрических или пространственных ошибок). Разработка СИМ-модели АСА является одним из этапов проектирования системы активной защиты (САЗ) от утечки конфиденциальной информации (КИ) через нее [8-9].

Открытым, однако, остается вопрос о том, в каком виде полученные результаты могут быть использованы при проектировании конкретных вариантов САЗ КИ – в первую очередь это касается типов ошибок, подлежащих моделированию, а также числовых параметров их вероятностных моделей. Экспериментальные материалы, которые можно было бы принять в качестве исходных данных при проектировании таких САЗ, в необходимом объеме сегодня отсутствуют.

На восполнение данного пробела в теории и практике моделирования АСА направлены [10] и настоящая статья.

Геометрию внешней задачи СТА иллюстрирует рис. 1: прямоугольная АСА с размерами I x h расположена на поверхности S_A , совпадающей с плоскостью X0Y системы глобальных декартовых координат; расстояние от S_A до плоскости S_М , в которой определяется структура ЭМП, равно R_A ; расстояние от элемента АСА, расположенного в точке М_А на поверхности S_A , до точки наблюдения М_S на плоскости S_М есть r_A .

Будем считать, что источник ЭМП, расположенный слева от S_A в точке М₀ с координатами Х₀ ; Y₀ ; Z₀ , создает в раскрыве АСА сложное по структуре возбуждающее поле Eq с круговой частотой ^ kt соответствующей k -ой гармонике его частотного спектра. Как это принято в СТА, будем также считать, что Eq можно представить в виде суперпозиции детерминированной (регулярной) и случайной (нерегулярной) составляющих. На регулярное поле, квазиравномерное в пространстве по амплитуде и фазе, накладывается стохастическая составляющая в виде совокупности амплитудных и фазовых ошибок, представляющих собой случайные отклонения от регулярных распределений амплитуд и фаз (значения которых в рамках метода СИМ «разыгрываются» с помощью компьютерной технологии метода Монте-Карло для заданного – в нашем случае равномерного закона [1-3; 8-9]). Исходные данные для проведения СИМ могут быть конкретизированы и уточнены экспериментальным путем, а в тестовых случаях – при помощи расчетных соотношений.

Рис. 1 иллюстрирует также схему лабораторного эксперимента, призванного показать правомерность применения подхода СТА к рассматриваемой ситуации [1-2]. Физической моделью АСА является одиночное прямоугольное отверстие в плоском проводящем экране, которое на частоте 10 ГГц возбуждается излучателем в виде открытого конца волновода с поперечным сечением 23×10 мм2. Если изменять координаты этого излучателя м№0) некоторым заданным (случайным или детерминированным) образом, фазы сигналов, возбуждающих разные точки МА, будут изменяться – что может быть эквивалентно появлению фазовой ошибки в АСА при отсутствии амплитудных ошибок. Прогнозируемые значения фазовой ошибки достигают МмАХ = ±180º при RA = 2 м; l = 0,15 м; h = 0,18 м; И [–0,04; 0,1] м. A

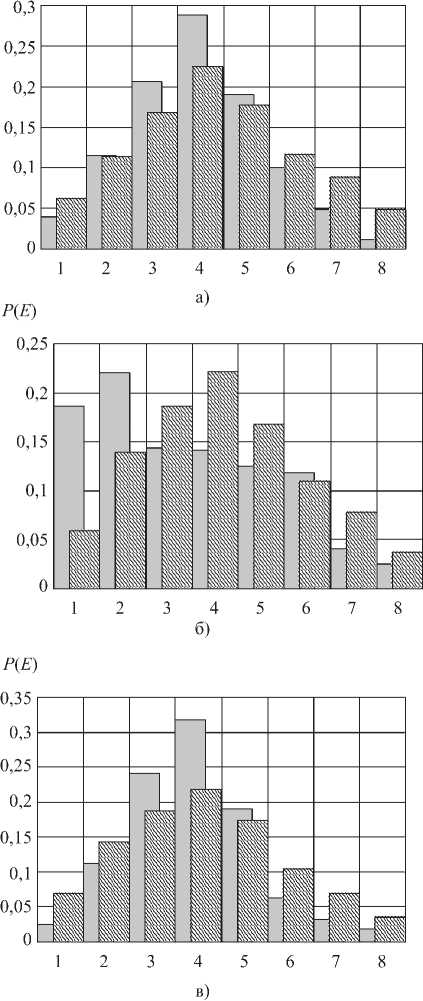
Рис. 2. Совмещенные гистограммы распределения уровней напряженности поля для физической модели АСА (слева – экспериментальные; справа – полученные методом СИМ) в точках, показанных на рис. 1 а) M ₁ ; б) M ₂ ; в) M ₃

на рис. 2

Точка	Мх	М2	М3
Эксперимент
Пределы; В/м	2,15 9,33	1 10,6	3,35 ... 14,45
Шаг; В/м	0,9	1,2	1,4
Расчет методом СИМ
Пределы; В/м	1,25-10’ ... 0,415	1,8-10’ ... 0,36	9.9-101 ... 0,22
Шаг; В/м	0,05	0,045	0,025

Проводя данный эксперимент N >> 1 раз при разных значениях ^0^0, можно сравнить полученные гистограммы уровней Е в заданной точке M_S на плоскости S_M – далее для краткости Е(М^ – с аналогичными гистограммами, которые найдены методом СИМ для фиксированных значений ^ФмАХ . Степень взаимного соответствия этих гистограмм будет говорить о допустимости (или недопустимости) использовать понятие «фазовая ошибка».

При проведении физического эксперимента возбуждающий излучатель последовательно перемещался по узлам прямоугольной сетки в пределах ^0’^0 с шагом 0,01 м. Три варианта выбора точки MS соответствовали M1 (0; 0; 2), M2 (0; 0,25; 2) и M3 (0;0,5;2), как это показано на рис. 1. Поскольку результаты определения E(MS) методом СИМ зависят от Мм.» и числа корреляционных кластеров [1-3] в раскрыве АСА ^' КЛ ’ простран- ство параметров для них является двумерным – это позволяет использовать представление их в виде трехмерной поверхности. Оценка степени взаимной близости экспериментальных и расчет- ных гистограмм производилась с применением критерия ст по методу наименьших квадратов

(МНК) как СУ = мер интервала;

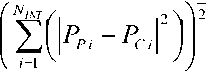
где i – но-

^PPi ^{И P}Ci – частота попадания

в i-ый интервал, соответственно, для эксперимен- тальной (левой на рис. 2) и расчетной (правой на рис. 2) гистограмм.

Выбор числа интервалов N/nt = 8, используемых при построении гистограмм, был продиктован, с одной стороны, требованием желательной нагляд- ности и точности их последующего сравнения, с другой стороны – стремлением избежать влияния недостаточно большого объема выборки (330 ≤ W ≤ 616) при проведении физического эксперимента.

Таблица 1. Параметры совмещения гистограмм P ( E )

Для каждой пары ^Фмах ^и ^кл определялись значения О' , минимум которого соответствует наилучшему совпадению сравниваемых гистограмм. Хотя, в принципе, о является случайной величиной, статистический анализ ее свойств не проводился, и для уменьшения влияния вариативности О исследовались 10⁴ реализаций EWsY Эксперименты СИМ проводились при значениях N_Kn = 4; 9; 16; 25; 36; 49; 64; 144 и 256; МмАХ [10°; 180°] с шагом 10°.

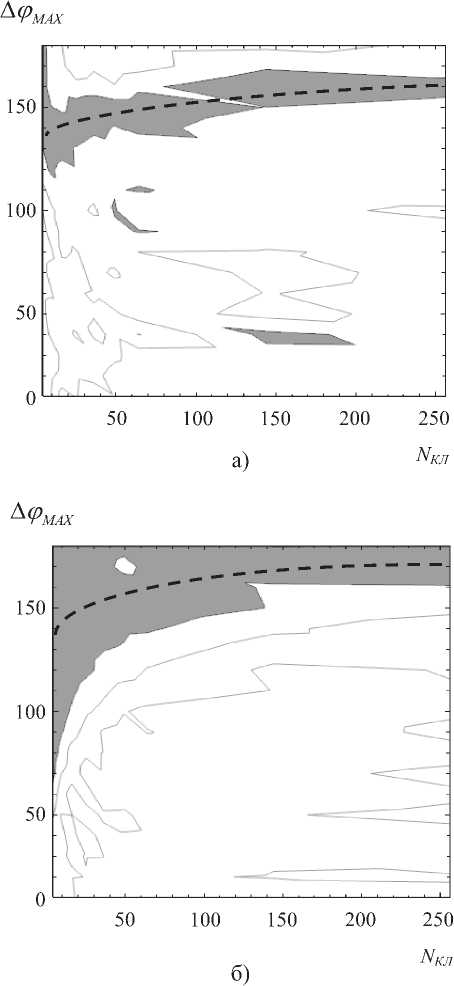
Рис. 3а-б. Графики зависимости от значений ^ФмАХ ^И ^КЛ '

• а)    для M ₁ (0;0;20);

• б)    для M ₂ (0;2,5;20)

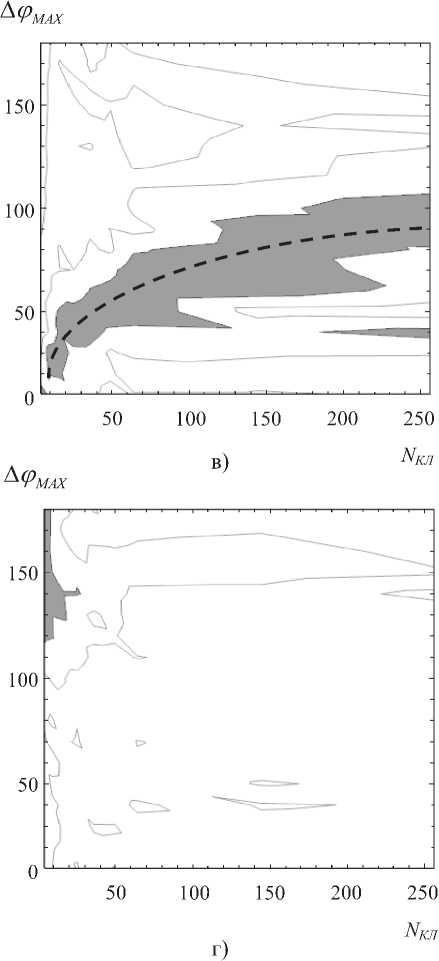
Рис. 3в-г. Графики зависимости ст от значений ^Фмах ^и N_кл :

в) для M ₃ (0;5;20);

г) для всех трех точек

Другие параметры СИМ-модели выбирались эквивалентными параметрам физической модели АСА с учетом масштаба 10:1 – при котором 1 м для физической модели АСА «равняется» 10 м для ее СИМ-модели. Гистограммы Е<М^ для всех точек M ₁… M ₃ приводились к общему относительному диапазону из 8 интервалов, параметры которых указаны в таблице 1.

Результаты определения зависимости о от значений ^Ф_М.4Х и "^кл представлены на рис. 3а-г. Критерием приемлемого соответствия гистограмм ES> друг другу является условие О' ≤ 0,25 (соответствующие ему области на рис. 3а-б и рис. 3в-г зачернены).

Из графиков рис. 3а-б, соответствующих точкам М ₁ и М ₂, близким к оси Z на рис. 1, видно, что при Мм.АХ = 140°… 180° достаточно обширная зона наилучшего совпадения гистограмм Е(М^ мало зависит от числа кластеров N ^л , определяющего корреляционные свойства поля возбуждения АСА (см. также «средние» графики, показанные утолщенными штриховыми линиями). В более удаленной от оси Z точке М ₃ (см. рис. 3в) указанная зона соответствует Мм.АХ ≤ 100°, хотя качественная картина та же.

Поэтому имеет смысл оценить общую зону взаимного соответствия экспериментальных и расчетных гистограмм для всех трех точек М1 …

М ₂, используя критерий ^общ

, где

СУ; – значение критерия МНК, полученное для i-ой точки (см. рис. 3а-в), i [1; 3]. График ^общ ’ представленный на рис. 3г, показывает резкое уменьшение указанной зоны (по-видимому, за счет влияния О" 3 – см. рис. 3в), которая в данном случае соответствует МмАХ = 130°… 180° и N [^л ≤ 9. Условию ^"общ ≤ 0,25 здесь удовлетворяют только три точки: МмАХ = 160°; 170° и 180° при ^кл = 4.

Изложенное показывает, что путем проведения экспериментальных измерений на лабораторных моделях и реальных объектах, анализируя производственно-технологические материалы и расчетные данные, а также реализуя другие исследовательские действия в рамках экспертного, вероятно стно-статисти-ческого и теоретико-вероятностного подходов, которыми располагает современная теория управления сложными системами [5], можно существенно уменьшить неопределенности, присущие исходным данным для проведения СИМ при исследования АСА. Представленные в статье результаты подтверждают правомерность применения понятия «фазовая ошибка» при исследовании работы АСА в гармоническом режиме и выбранные для проведения СИМ в качестве исходных данных на частотах выше 20 МГц значения N ≤ 16 и ^ф = 60° ’                       —           т МАЛ.

… 180° [1-3].