Моделирование вероятностных распределений с «Тяжелыми хвостами»
Автор: Маслов Олег Николаевич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 1 т.9, 2011 года.
Бесплатный доступ
Обсуждается возможность моделирования распределений случайных величин с так называемыми «тяжелыми хвостами» при помощи одномерных устойчивых законов.
Случайные величины, законы распределения, "тяжелые хвосты", устойчивые вероятностные модели
Короткий адрес: https://sciup.org/140191458
IDR: 140191458 | УДК: 621.395.4
Текст научной статьи Моделирование вероятностных распределений с «Тяжелыми хвостами»
Введение. Постановка задачи
Наличие «тяжелых хвостов» (далее без кавычек) у плотности распределения вероятности (ПРВ) случайной величины Х существенно затрудняет ее компьютерное моделирование. Хвосты у ПРВ обычно появляются в результате обработки экспериментальных гистограмм, когда выясняется, что полученные данные хорошо соответствуют нормальному закону лишь в центральной части области распределения случайной величины X [– Xm ; Xm ].
Иллюстрацией служит рис. 1, где показаны экспериментальная гистограмма 1 и два варианта ее аппроксимации: нормальный закон (сплошная линия 2) и более сложная модель учитывающей тяжелый хвост гистограммы (точечная кривая 3).
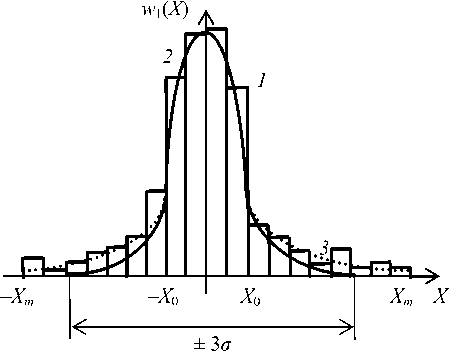
Рис. 1. Симметричная ПРВ w 1 ( X ) с тяжелыми хвостами справа и слева: 1 – экспериментальная гистограмма; сплошная линия 2 – гауссовская ПРВ; точечная кривая 3 – тяжелый хвост реальной ПРВ
На практике ситуация осложняется и тем, что центральная область является статистически хорошо насыщенной, а краевые области более «бедны», поскольку соответствуют существенно меньшему объему полученных данных (гистограммы здесь часто являются решетчатыми, «дырявыми», с выбросами и пропусками), что экспериментатор обычно связывает с несовершенством методики и малым временем проведения измерений.
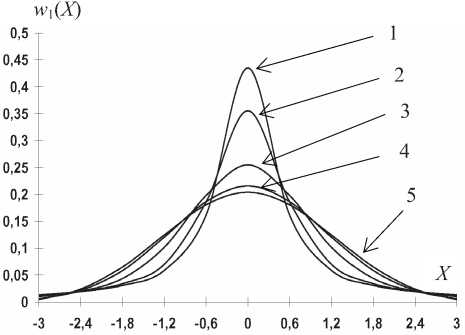
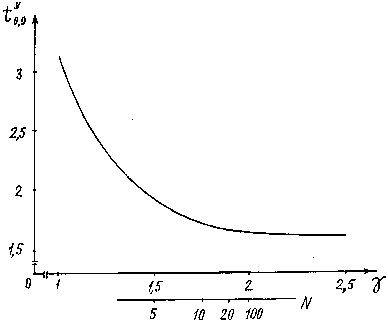
Нормальный закон (гауссовская кривая) при исследовании случайных величин в бесконечных пределах X [–∞; ∞] обладает рядом замечательных качеств [1-4]. Во-первых, его одномерная ПРВ может быть записана в удобном аналитическом виде w, (Л") = (1 / V2^ В-третьих, (1) соответствует достаточно широкому кругу условий применимости центральной предельной теоремы (ЦПТ) теории вероятностей (ТВ) [1-2], которые на практике выполняются почти всегда – если не абсолютно строго, то приближенно, чего вполне достаточно для решения прикладных задач [3-4]. Из недостатков (1) выделим два: во-первых, интегральная функция распределения (ИФР) нормального закона P(X) = ^w^X^dX (2) выражается через специальные функции: интеграл вероятности, функцию Лапласа и т.п., что долгие годы осложняло ее практическое применение (сегодня это не так существенно, поскольку любые исследования ИФР можно произвести численными методами). Во-вторых, что наиболее важно, согласно правилу «трех сигм» за пределами интервала ± 3σ (см. рис. 1) значений Х, влияющих на результаты проводимых исследований, не должно быть, а если по экспериментальным данным они есть – то даже фундамент в виде ЦПТ ТВ не выручает модель (1)-(2). Во всех ее модификациях – односторонний, усеченный и ограниченный нормальный закон, логариф-мически-нормальный закон, закон распределения модуля нормальной случайной величины – правило «трех сигм» и проблема тяжелых хвостов так или иначе проявляют себя. Цель статьи – анализ возможностей, которые дает применение в интересах компьютерного анализа и моделирования ПРВ w1(X) с тяжелыми хвостами некоторых относительно новых результатов современной ТВ. Пути решения проблемы Известны три способа решения проблемы тяжелых хвостов, связанные с разным пониманием причин их возникновения. 1. Появление тяжелого хвоста объясняется методическими и инструментальными погрешностями при проведении экспериментов. Логика здесь такова: поскольку тенденция к нормализации ПРВ наблюдается, начиная с трех и более факторов, влияющих на результаты измерений, условия применимости ЦПТ ТВ выполняются практически всегда и закон (1)-(2) должен иметь место, отклонения от него – это выбросы или ошибки, на которые не следует обращать внимание. Методики обработки статистических данных в развитие этой идеи предлагают даже отбрасывать оговоренное число минимальных и максимальных значений Х, искусственно «подгоняя» эксперимент под условия ЦПТ ТВ. Корректно избавиться от тяжелых хвостов, впрочем, удается далеко не всегда. 2. К центральной части сплошной кривой 2 на рис. 1 предлагается «пришить» тяжелые хвосты, соответствующие точечной кривой 3. Основанием для такой кусочной аппроксимации считаются, например, различие между законами замираний разной глубины для многолучевого сигнала 3. Появление тяжелого хвоста объясняется формированием Х в условиях применимости обобщенной ЦПТ ТВ [2], приводящей в качестве предельных распределений к семейству одномерных устойчивых законов. Особенностью данных законов является простота их исследования с помощью метода характеристических функций (ХФ), тогда как ПРВ и ИФР в аналитическом виде для них могут быть записаны лишь в небольшом числе частных случаев. Каноническое представление ХФ устойчивого закона имеет вид [1-3] /‘(и) = exp pan —b\ z/|z 11+jc(u/1 г/ |)Q(w,/)]}, (3) Рассмотрим конкретный пример [3]. При исследовании структуры электромагнитного поля (ЭМП) в просторном учебном помещении, окна которого выходили на телецентр, измерения проводились на каждом квадратном метре его площади, на двух высотах. После обработки основного массива данных, относящихся к центральной части помещения, было установлено, что они для области уровней ЭМП X [X m1 ; X m2 ], границы которой определяются динамическим диапазоном измерительной аппаратуры, соответствуют усеченному нормальному закону (1)-(2). Это представлялось понятным, поскольку уровни ЭМП в помещении можно было считать случайными функциями, зависящими от большого числа аргументов (случайных факторов), соизмеримых по влиянию на Х – что полностью соответствует условиям применимости ЦПТ ТВ. Но тяжелый хвост у гистограммы Х появился после учета сравнительно небольшого по объему экспериментального материала, относящегося к дверным и оконным проемам – поскольку уровни ЭМП здесь по очевидным причинам были существенно выше, чем в глубине помещения. Проигнорировать данный факт, сославшись на ЦПТ ТВ и рекомендацию отбрасывать лишние результаты измерений, было бы явной натяжкой. в радиоканале, разные свойства волоконно-оптического канала при больших и малых уровнях сигнала и т.п. Развитием данной идеи является аппроксимация с требуемой точностью гистограммы 1 на рис. 1 совокупностью любых подходящих функций из пакета прикладных программ, которым располагает экспериментатор. Специфика такого подхода состоит в следующем. Если цель проводимого эксперимента – определение статистических характеристик объекта для оперативного управления им, то на рис. 1 вообще ничего не нужно аппроксимировать, поскольку необходимые оценки для числовых параметров Х могут быть получены непосредственно из экспериментального материала, даже без построения гистограммы. Если же эксперимент преследует исследовательские цели, то выбор аппроксимации ПРВ w1(X) привязан к гипотезе о характере происхождения и вероятностных свойствах Х – например, если ПРВ соответствует нормальному закону, то Х возникает в условиях применимости ЦПТ ТВ, если ПРВ – закон Коши, то при формировании Х используются операции деления случайных величин друг на друга, и т.д. Этот момент еще более усиливается при моделировании поведения объекта – поскольку любая аппроксимация описывает свойства Х в прошлом, но ничего не прогнозирует на будущее. Тогда как целью моделирования является воспроизведение вероятностных свойств Х в интересах исследования, проектирования и предсказания, главным образом, будущего поведения объекта. Приведем второй пример. Полигауссовы модели позволяют реализовать достоинства (1)-(2) при решении целого ряда практически важных задач [4] в рамках обоих подходов, однако ограничением при моделировании здесь является допущение о том, что композиции гауссовских законов должен соответствовать набор моделируемых величин, подчиняющихся ЦПТ ТВ. Другими словами, чтобы построить адекватную и надежную полигауссову модель, необходимо произвести декомпозицию моделируемой системы на части, каждой из которых должна соответствовать гауссова модель, чтобы затем «собрать» из этих частей систему, которой будет соответствовать полигауссова модель. «Аналогично базовой роли полигармони-ческих моделей и частотных спектров Фурье в теории детерминированных радиосигналов, в статистической радиотехнике можно ожидать сохранения базовой роли систем гауссовских распределений, порождающих полигауссов базис из линейно независимых функций в пространстве распределений вероятности на многообразиях физически реализуемых сигналов и помех, а также преобразования Гаусса и вероятностных спектров Гаусса» [4]. В соответствии с данным тезисом для полигауссовой модели вводятся ПРВ и гауссовский спектр средних величин (выражаемый через характеристическую функцию моделируемой случайной величины), которые связаны между собой одноименным преобразованием. Проблема тяжелого хвоста ПРВ при этом фактически теряет актуальность – поскольку аппроксимационные возможности у полигауссовой модели весьма велики. Впрочем, как и у других универсальных моделей типа показательно-степенного закона или вообще у полинома n-ой степени. где z/[-co,oo]; tz[-oo,oo]; Z>[0;co]; c[-l, 1]; /(0,2], причем tgpryl2Y /*1; (2/ д') In | w |, / = 1. Q (г/, /) Из (3) видно, что устойчивый закон является четырехпараметрическим, поскольку ХФ зависит от параметров a, b, с и у. Параметр Y называется характеристическим показателем устойчивого закона. Нормальный закон следует из (3) при y=T, а = Хй\Ь=огП.Закон Коши имеет место при y= 1; c = 0 ; a = P; b = ц. Перечислим основные свойства устойчивых распределений в области X[-oo, co]: - все устойчивые законы являются одновершинными; - непрерывные устойчивые законы в каждой точке Х имеют производные всех порядков; - каждый устойчивый закон с характеристическим показателем Y имеет конечные абсолютные моменты всех порядков 5< y. Поэтому только нормальный закон в области Х [—00, oo] имеет конечную дисперсию: при 5= y= 2. Конечное среднее значение имеют устойчивые законы при У > 1; в случае 0 < У< 1 устойчивые распределения не имеют ни среднего значения, ни дисперсии (соответствующие им интегралы в бесконечных пределах расходятся); - физический смысл параметров а и b устойчивого закона можно определить вычислением среднего значения и дисперсии распределения с ХФ f(и): при У> 1 среднее значение т1 (Х) = ; при у = 2 (нормальный закон) дисперсия D{Х} = 2b; - в общем случае «и ft являются параметрами сдвига и изменения масштаба ПРВ устойчивого закона, они сравнительно мало влияют на ее форму. Напротив, параметры У и с существенно влияют на кривую ПРВ: У определяет ее эксцесс, а с - асимметрию, то есть непосредственным образом участвуют в формировании тяжелого хвоста; - важное для практики ограничение У < 2 обусловлено тем, что соответствующая ХФ (3) ПРВ при X [-со, со] должна быть положительно определенной, поэтому модели такого рода при у > 2, формально соответствующие определению устойчивости ХФ, могут быть использованы для компьютерного моделирования лишь в области X [X m1 ; X m2 ], где w1(X) > 0. В отличие от законов с / < 2, в [3] предложено именовать такие модели формально устойчивыми распределениями. В этой связи продемонстрируем третий пример. В [5] представлены результаты исследования методом статистического имитационного моделирования (СИМ) коэффициента превышения ZN -^nN^CN^ – защитного отношения «помеха/сигнал» в системе активной защиты информации, где VПN и VCN – относительные уровни (множители ослабления напряженности поля свободного пространства), соответственно, помехи и сигнала, распределенные по устойчивому закону и коррелированные между собой. На рис. 2 представлены результаты сравнения вероятности Pi (zN) попадания zN [0; 10] в интервалы с номерами i [1; 20], длина каждого интервала 0,5; для нормально распределенных VПN и VCN (при γ = 2) левые гистограммы соответствуют тестовому аналитическому расчету, правые – результатам СИМ при числе реализаций NZ = 5.103 для коэффициента корреляции Ro = 0,5. С помощью метода СИМ аналогичные данные были получены и в более общих условиях: при γ = 1,2…2,2; Ro = 0,05…0,99. Рис. 2. Результаты аналитического расчета и СИМ для zN при γ = 2; Rо= 0,5 В итоге было показано, что при разных сочетаниях γ и Ro форма и параметры ПРВ коэффициента превышения zN могут соответствовать достаточно разным вероятностным моделям: от односторонних гиперболического, экспоненциального и распределений типа Коши до усеченного нормального закона, при Ro → 1 вырождающегося в дельта-функцию Дирака. Поскольку в данном случае речь идет об отношении случайных величин VПN и VCN , тяжелые хвосты у ПРВ присутствуют в абсолютном большинстве рассматриваемых случаев. Устойчивые законы, как и полигауссовы модели, могут быть использованы и для аппроксимации гистограмм, и для моделирования поведения объектов. Рассмотрим их уникальные в этом отношении свойства. Особенности практического применения устойчивых моделей Финитные устойчивые модели сочетают возможность эффективной компьютерной аппроксимации гистограмм с тяжелыми хвостами (путем варьирования параметров а, Ь, с и у) в области X [X m1 ; X m2 ], что необходимо для анализа состояния объекта в прошлом с возможностью описания настоящего и будущего состояния объекта (причем даже с малой прецедентной базой: из числа проектируемых, разведанных, инновационных), поскольку опираются на прочный фундамент обобщенной ЦПТ ТВ, что в определенной мере гарантирует надежность и достоверность результатов прогнозирования. Для перехода от ХФ f (и) к ПРВ w1(X) и ИФР P(X) необходимо выполнить обратное преобразование Фурье w, (20 = (1 / 2лр J/ (и) exp(-ju X^du , (4) причем функция ПРВ должна отвечать условию нормировки jw1(x)c/x = l-£o, (5) где ^« 1 – заданная малая величина, регулирующая точность расчета, а и [и т1 , и т2 ], Х [Х т1, Х т2 ], согласно [3], соответствуют существенной области одномерного преобразования Фурье (4). Границы этой области в [3] было предложено определять на основании правила Парсеваля, подобно тому как это делается в теории спектров: через сравнение результатов интегрирования произведения ХФ f (и) и комплексно-сопряженной функции f *(и) в бесконечных и[–∞,∞] и конечных и[–ит, ит] пределах u) f*(u)du ptu,)-^ - = i-^, m J/(m) /4^) du где ε << 1 – параметр, аналогично 8 регулирующий точность расчета. Отметим, что новые возможности для определения ПРВ и ИФР устойчивых моделей дает применение современных пакетов прикладных программ, представленных в Internet, которые появились на 20 лет позже, чем [3]. Для краткости изложения и отдавая дань традициям ТВ, дальнейшие утверждения сформулируем в виде теоремы, доказательство которой содержат [1-2 и др.], а также сводки выводов и примечаний к ней. Теорема. Если моделируемая случайная величина Х является суммой Ns >> 1 слагаемых Хs, соответствующих условиям применимости постоянно расширяющегося круга обобщений ЦПТ ТВ, то естьx = Ух,,и если в области X [Xm 1 ? -^m2] при Ns ^> oo для последовательности Х будет существовать предельное (асимптотическое) распределение, реализуемое единственным образом, то этим распределением будет устойчивый и никакой другой закон (3). Для выполнения условия нормировки (5) в области X [Xm ।, Xm21 устойчивый закон должен быть усечен. Вывод 1. Для моделирования статистических свойств случайных величин, моделирующих факторы воздействия на объект в условиях применимости постоянно расширяющегося круга обобщений ЦПТ ТВ, применим усеченный устойчивый закон. Примечание 1. Если доказана предельная сходимость последовательности Х к устойчивому закону для области [Xml > Xm2^? то при изменении ее границ вид ХФ (3) не изменяется. Примечание 2. Если схема формирования Х является более сложной – например, за счет учета связей ХS , как детерминированных, так и случайных, то вместо обычного суммирования в теореме фигурирует обобщенное (понимаемое как набор полугрупповых операций, ассоциативных и коммутативных: сложение, умножение, возведение в степень и т.д. [1]). Вид ХФ (3) при этом не изменяется. Примечание 3. Поскольку при моделировании реальных случайных величин и факторов воздействия на объект случайные аргументы в обобщенной сумме заведомо удовлетворяют условиям ЦПТ ТВ [1-2], операции центрирования и нормирования Х при «подготовке» их к определению для них предельных устойчивых распределений, даже с учетом условий Xs>0;X>0, представляются излишними – тем более что речь в итоге идет об асимптотических, то есть всегда приближенно выполняемых соотношениях. Примечание 4. Финитные устойчивые модели имеют числовые характеристики, зависящие не только от параметров a, b, с и /, но и от границ области X [Xm ], Xm2^ ? что соответствует реальным условиям. В частных случаях при / = 1 числовые характеристики (4) соответствуют усеченному закону Коши, а при У = 2 – усеченному нормальному закону. Примечание 5. Финитные ПРВ с / > 2 по терминологии [3] именуются формально устойчивыми моделями: они не связаны с ЦПТ ТВ, однако могут возникать, например, в результате нелинейных преобразований моделируемых случайных величин. При / > 2 коэффициент эксцесса ПРВ (4) является положительным, для формально устойчивых ПРВ (при / > 2 ) он отрицателен. Примечание 6. Соответствующая (3) центрированная (a = 0) и симметричная (с = 0) функция ПРВ, с учетом нормирующего множителя AN , имеет вид wx(X) = (\/^An) Jexp(-bu'")cos(u X)du, U) 0 где u [ 0; Um]; Um – граница существенной области преобразования Фурье [3]. Типовые графики ПРВ w1( Х ) при a = c = 0; b = 0,5 и у = 1 (кривая 1); 1,5 (кр. 2); 2 (кр. 3); 2,5 (кр. 4) для Х [– 3; 3] представлены на рис. 3. Рис. 3. ПРВ w1(X) для финитных моделей на основе одномерных устойчивых распределений при b = 0,5 иY = 0,8 (кр. 1); 1 (кр. 2); 1,5 (кр. 3); 2 (кр. 4); 2,25 (кр. 5) закон Стьюдента удовлетворительно аппроксимирует распределения моделируемых величин в условиях применимости обобщенной ЦПТ ТВ, чем и обусловлено его применение до настоящего времени [9]. Примечание 8. Расчет величины погрешности A p с заданной вероятностью р [0; 1] подробно рассматривается в [7]: в частности, дается обоснование выбора р = 0,9 для симметричных центрированных ПРВ, которые могут моделироваться законами Стьюдента, нормальным, устойчивым и т.п. Вероятность попадания случайной величины Х в симметричный интервал [ – tp ; tp ] равна ^,(| ^|р) = 2 Jw,(^)^. (8) Остановимся на применении устойчивых моделей в интересах теории организации и планирования эксперимента [7-9], где часто встречаются ПРВ с тяжелыми хвостами. Устойчивые модели и законы из семейства Стьюдента Примечание 7. Устойчивая модель (3)-(4) может быть сопоставлена с законами из семейства Стьюдента, которые широко используются при планировании эксперимента и расчете погрешностей [7]. Анализ показывает, что с ростом числа измерений N законы из обоих семейств приближаются к нормальному ( Y = 2). В другом предельном случае Y = 1 оба закона переходят в распределение Коши, обладающее ярко выраженным тяжелым хвостом. Указанное соответствие может быть истолковано следующим образом: закон Стьюдента приближенно справедлив при больших выборках данных (N >> 1), поскольку для них распределения моделируемых величин нормализуются. При малом объеме выборок закон Стьюдента также остается приближенно верным – за счет того, что параметр используемого нормального закона (найденный через оценку среднего квадратического отклонения – СКО) считается случайным [8]. Хотя, строго говоря, для распределений, отличных от нормального, использование законов из семейства Стьюдента некорректно [7-8]. Устойчивый закон (3)-(4) в рассматриваемой ситуации остается справедливым всегда: при малом объеме выборок имеет место Y< 2, тогда как с ростом N, для больших выборок данных, У ^2,что полностью соответствует выводам теоретического анализа [1-3]. Таким образом, Квантили t0,9 распределений Стьюдента и нормального закона для двухстороннего симметричного доверительного интервала при р = 0,9 приведены в [7-8 и др.]. Аналогичные квантили устойчивого закона можно найти, представив для него (8) как Л=(2/л-) |exp(-bu7)sin(utp)du/u. (9) о Квантили t0,9 устойчивого закона следуют из (9) при Pt = 0,9; а для нормального распределения – еще и при Y = 2. Алгоритм численного расчета (9) аналогичен [5]. На рис. 4 представлен график зависимости квантиля t0,9У и прогнозируемого числа измерений N для устойчивого закона с фиксированной дисперсией D = 2 от параметра Y = 1 ... 2,5. Из рис. 4 видно, что неточность априорного задания формы w1(X) при Y > 1,5 в данном случае приводит к ошибке при определении t0,9У не более чем на 17% по сравнению с нормальным законом (более подробно см. [9]). Вывод 2. Границы доверительного интервала ± ^0,9 при р = 0,9 в условиях применимости ЦПТ ТВ целесообразно искать по формуле A 0,9 - to ^ Sq/ -x[N\ где S0 – ожидаемая оценка S (будущий эмпирический стандарт ошибки). При этом отличие S0 от истинного значения S здесь учитывается путем использования в расчете квантиля устойчивого закона t0,9У вместо нормального, и надобность в распределениях Стьюдента (базирующихся на нормальной модели, но дающих существенно другой результат по сравнению с ней) отпадает. Рис. 4. Зависимость квантиля t0,9У и числа измерений N от параметра для устойчивой модели с фиксиро ванной дисперсией D = 2 Примечание 9. При планировании эксперимента важное значение имеет прогноз минимального объема данных, гарантирующих репрезентативность выборки с заданной вероятностью. Если число измерений N >> 1 и условия нормализации ПРВ w1(X) выполняются, для у= 2 квантиль t0,9У = 1,645 и расчет N согласно (10) при заданной точности g ^0,9/ ^° не представляет труда [7]. Для меньших объемов выборки (на практике при N< 3…10) использование законов Стьюдента приводит к затруднению ввиду того, что значения t0,9С и N = m + 1 однозначно связаны друг с другом [8], что представляется важным – вне зависимости от значений параметров m и g. В этом также проявляется противоречивость законов Стьюдента, которые, строго говоря, неприменимы для анализа и моделирования случайных величин с распределениями, отличными от нормального. Примечание 10. Использование устойчивых законов в рассматриваемой ситуации снимает все противоречия. Необходимое число измерений определяется согласно (10) как N=(t0//g\ (11) причем, по данным рис. 4, увеличение N не более чем в 1,37 раза по сравнению с нормальным законом и не более чем в 1,21 раза по сравнению с законами Стьюдента гарантирует соответствие выборки экспериментальных данных требуемой точности измерений при доверительной вероятности р = 0,9. Подчеркнем, что данный результат получен вне зависимости от предположения о нормальности распределений моделируемых величин при проведении эксперимента [9]. Заключение Проблему тяжелых хвостов ПРВ можно решить тремя способами: обеспечивая соответствие условий проведения эксперимента условиям применимости ЦПТ ТВ; аппроксимируя экспериментальные гистограммы совокупностью заданных вероятностных функций и используя финитные модели, построенные на основе одномерных устойчивых распределений, соответствующих условиям применимости обобщенной ЦПТ ТВ. Подбирая параметры аппроксимационной модели, можно обеспечить ее соответствие с заданной точностью любому экспериментальному материалу, характеризующему поведение объекта в прошлом. Однако нет гарантии, что в будущем эта модель не окажется некорректной и будет пригодна для предсказания поведения объекта (особенно с малой прецедентной базой). В условиях применимости ЦПТ ТВ моделирование характеристик объекта целесообразно производить с использованием нормальной модели (1)-(2), в условиях применимости обобщенной ЦПТ ТВ – с помощью устойчивой модели (3)-(4), которая включает нормальную модель в качестве частного варианта при у = 2. Представляет интерес исследование механизмов возникновения тяжелых хвостов ПРВ: отражающих условия обобщения ЦПТ ТВ при проведении эксперимента, декомпозицию моделируемого вероятностного закона на исходные компоненты, формирование мультимедийного потока данных из простых пуассоновских составляющих и т.п. Мощным средством решения такого рода задач является компьютерный метод статистического имитационного моделирования [5-6]. Самостоятельное значение имеет разработка методов и средств построения вербальных (словесных) моделей сложных объектов путем описания их свойств и принципов функционирования, а также применение моделей состава и структуры объектов, статических и динамических, стационарных и нестационарных моделей. Прогнозирование будущего поведения объекта методом компьютерного моделирования целесообразно проводить, проверяя полученные выходные результаты на робастность (устойчивость по отношению к динамике входных данных). Это легко и просто делать с помощью единой, максимально общей и универсальной устойчивой модели, опирающейся на обобщенную ЦПТ ТВ, и практически невозможно или весьма неудобно – используя набор эмпирических моделей. В простейшем случае проверка на робастность выход- ных результатов сводится к варьированию параметров ку ; с и др.) входной устойчивой модели. При прогнозировании точности результатов эксперимента (как физического, так и компьютерного) применение финитных устойчивых моделей позволяет избежать противоречий, присущих использованию в этих целях семейства распределений Стьюдента.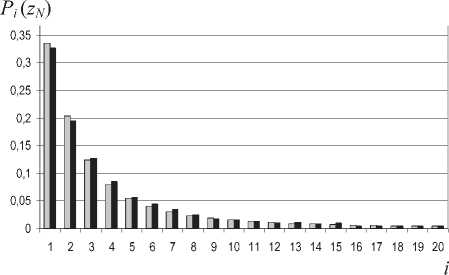
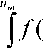
Список литературы Моделирование вероятностных распределений с «Тяжелыми хвостами»
- Золотарев В.М. Современная теория суммирования независимых случайных величин. М.: Наука, 1986. -416 с.
- Учайкин В.В. Метод дробных производных. Ульяновск: Изд. «Артишок», 2008. -512 с.
- Маслов О.Н. Устойчивые распределения и их применение в радиотехнике. М.: Радио и связь, 1994. -152 с.
- Чабдаров Ш.М., Надеев А.Ф., Файзуллин Р.Р. и др. Полигауссовы модели и спектры в посткорреляционных разделах статистической радиотехники//Доклады IX МНТК «Проблемы техники и технологий телекоммуникаций». Казань, 2008. -С. 37-44.
- Маслов О.Н., Раков А.С. Статистические характеристики коэффициента превышения в системе активной защиты информации//ИКТ. Т. 7, № 4, 2009. -С. 107-116.
- Маслов О.Н. Развитие математических принципов метода статистического имитационного моделирования//Избранные труды Российской школы «К 70-летию Г.П. Вяткина». М.: РАН, 2005. -С. 539-550.
- Новицкий П.В., Зограф И.А. Оценка погрешностей результатов и средств измерений. Л.: Энергоатомиздат, 1991. -304 с.
- Бендат Дж., Пирсол А. Прикладной анализ случайных данных. М.: Мир, 1989. -540 с.
- Маслов О.Н. Моделирование плотностей распределения погрешностей измерений с помощью устойчивых законов//Радиотехника. № 7, 1998. -С. 6-9.


