Моделирование вертикальных движений морской воды в стратифицированных водоемах
Автор: Кудинов Н.В., Филина А.А., Никитина А.В., Бондаренко Д.В., Развеева И.Ф.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 2 т.23, 2023 года.
Бесплатный доступ
Введение. В области вычислительной математики известно множество способов аппроксимации модели механики жидкости. Учеными выработаны методы и оценки критериев качества аппроксимации, таких как устойчивость и сходимость. Комбинация подходов построения экономичных разностных схем, таких как расщепление по физическим процессам, регуляризация по Б. Н. Четверушкину, линейная комбинация разностной схемы «кабаре» и «крест» в совокупности ранее не реализовывалась и не оценивалась. Перед авторами стояла задача аппроксимировать каждую часть расщеплённой по физическим процессам модели гидродинамики наиболее адекватной схемой и далее исследовать корректность данного подхода.Материалы и методы. Математическая модель гидрофизических процессов замыкается эмпирическим уравнением состояния соленой воды. Выбираются значимые свойства, строится математическая модель. Разностные операторы аппроксимируют дифференциальные операторы. Строится алгоритм послойного моделирования переходных процессов. Алгоритм реализован в виде программы, которая, в основном, содержит поэлементные (массивно параллельные) операции.Результаты исследования. Получены математические модели гидродинамических процессов в водоемах, учитывающие три уравнения движения при наличии градиента плотности водной среды при отказе от гидростатического приближения. Апробирован новый способ вычисления поля давления с применением регуляризаторов по Б. Н. Четверушкину в уравнении неразрывности. Разработан программный модуль численного моделирования гидрофизических процессов движения воды с различной солёностью и плотностью. Это открытое программное обеспечение, допускающее не только переопределение эмпирических зависимостей (как алгебраических функций), но и подключение внешних моделирующих модулей для отображения зависимостей алгоритмически.Обсуждение и заключение. Разработанная модель гидрофизики, учитывающая свойства солёной воды и динамическую связь механического движения воды с солёностью, может применяться для изучения формирования неравновесного распределения параметров и идентификации наиболее стабильных параметров водной среды. Модель объясняет нисходящее движение кислорода, что позволит в будущем оценивать величины параметров водной среды, которые сложно измерить непосредственно. Она может быть использована в процедуре параметрической идентификации трудноизмеряемых параметров водной среды.
Математическая модель, стратификация, модель динамики морской воды, квазигидродинамическая модель, метод заполненности ячеек, центрально-разностная схема, метод прогонки, ввцп, кабаре, крест
Короткий адрес: https://sciup.org/142238867
IDR: 142238867 | УДК: 004.942: | DOI: 10.23947/2687-1653-2023-23-2-212-224
Текст научной статьи Моделирование вертикальных движений морской воды в стратифицированных водоемах
Введение. В области вычислительной математики известно множество способов аппроксимации модели механики жидкости. Учеными выработаны методы и оценки критериев качества аппроксимации, таких как устойчивость и сходимость. Комбинация подходов построения экономичных разностных схем, таких как расщепление по физическим процессам, регуляризация по Б. Н. Четверушкину, линейная комбинация разностной схемы «кабаре» и «крест» в совокупности ранее не реализовывалась и не оценивалась. Перед авторами стояла задача аппроксимировать каждую часть расщеплённой по физическим процессам модели гидродинамики наиболее адекватной схемой и далее исследовать корректность данного подхода.
Материалы и методы. Математическая модель гидрофизических процессов замыкается эмпирическим уравнением состояния соленой воды. Выбираются значимые свойства, строится математическая модель. Разностные операторы аппроксимируют дифференциальные операторы. Строится алгоритм послойного моделирования переходных процессов. Алгоритм реализован в виде программы, которая, в основном, содержит поэлементные (массивно параллельные) операции.
Результаты исследования. Получены математические модели гидродинамических процессов в водоемах, учитывающие три уравнения движения при наличии градиента плотности водной среды при отказе от гидростатического приближения. Апробирован новый способ вычисления поля давления с применением регуляризаторов по Б. Н. Четверушкину в уравнении неразрывности. Разработан программный модуль численного моделирования гидрофизических процессов движения воды с различной солёностью и плотностью. Это открытое программное обеспечение, допускающее не только переопределение эмпирических зависимостей (как алгебраических функций), но и подключение внешних моделирующих модулей для отображения зависимостей алгоритмически.
Обсуждение и заключение. Разработанная модель гидрофизики, учитывающая свойства солёной воды и динамическую связь механического движения воды с солёностью, может применяться для изучения формирования неравновесного распределения параметров и идентификации наиболее стабильных параметров водной среды. Модель объясняет нисходящее движение кислорода, что позволит в будущем оценивать величины параметров водной среды, которые сложно измерить непосредственно. Она может быть использована в процедуре параметрической идентификации трудноизмеряемых параметров водной среды.
Original article
Simulation of Vertical Movements of Seawater in Stratified Reservoirs
Nikita V. Kudinov Э И1, Alena А. Filina 2, Alla V. Nikitina 10 1, Denis V. Bondarenko1, Irina F. Razveeva1
1Don State Technical University, Rostov-on-Don, Russian Federation
-
2 “Supercomputers and Neurocomputers Research Center” Co Ltd, Taganrog, Russian Federation И kudinov nikita@mail.ru
Introduction. In the field of computational mathematics, there are many ways to approximate the model of fluid mechanics. Methods and estimates of approximation quality criteria, such as stability and convergence, are developed, while a combination of approaches to constructing economical difference schemes, such as splitting by physical processes, regularization by B. N. Chetverushkin, a linear combination of the Upwind and Standard Leapfrog difference schemes in aggregate has not been implemented and evaluated before. The authors were faced with the task of approximating each part of the hydrodynamic model split by physical processes with the most adequate scheme and further investigating the correctness of this approach.
Materials and Methods. The mathematical model of hydrophysical processes is closed by the empirical equation of the state of salt water. Significant properties were selected, a mathematical model was built. Difference operators approximated differential operators. An algorithm for layer-by-layer modeling of transients was constructed. The algorithm has been implemented in the form of the program, which mainly contains elementwise (massively-parallel) operations.
Results. Mathematical models of hydrodynamic processes in reservoirs were obtained, taking into account three equations of motion in the presence of a density gradient of the aqueous medium when hydrostatic approximation was abandoned. A new method of calculating the pressure field using B. N. Chetverushkin’s regularizers in the continuity equation was tested. A software module for numerical simulation of hydrophysical processes of water movement with different salinity and density was developed. This is open-source software that provides not only the redefinition of empirical dependences (as algebraic functions), but also the connection of external simulating modules to display dependences algorithmically.
Discussion and Conclusion. The developed model of hydrophysics, taking into account the properties of salt water and the dynamic relationship of the mechanical movement of water with salinity, can be used to study the formation of a nonequilibrium distribution of parameters and identify the most stable parameters of the aquatic environment. The model explains the downward movement of oxygen. That will help in the future to estimate the values of the parameters of the aquatic environment, which are difficult to measure directly. It can be used in the procedure of parametric identification of hard-to-measure parameters of the aquatic environment.
Acknowledgements: the authors would like to thank AI Sukhinov, Corresponding Member, Russian Academy of Sciences, mentor of the scientific school, for organizing the research; and also, they express gratitude to the editorial board of the journal “Advanced Engineering Research” for the help provided in the preparation of the article.
Funding information. The research is done with the financial support from Russian Science Foundation (project no. 22–71–10102).
Введение. Одной из важных задач, связанных с экологией и безопасностью жизнедеятельности людей, живущих в прибрежных территориях, является прогнозирование и моделирование движения воды в морях и крупных региональных водоёмах. Кроме того, актуально изучение процесса переноса растворенных в водной среде веществ при учёте стратификации и зависимости плотности воды от многих переменных факторов. Такое прогнозное моделирование, вероятно, позволит не только оценивать качество вод, но и управлять им в условиях климатических изменений и индустриальных воздействий. Более общая и главная цель — связать качество вод с численностью и видовым разнообразим естественных гидробиоценозов, обитающих в гидросфере. При решении этих задач необходимо учитывать гидродинамические характеристики водной среды, особенности внешних факторов воздействия, таких как неоднородность распределения температуры, соленость, насыщенность воды кислородом, количество растворенных в воде газов, кислотность. Эти параметры являются одними из ключевых параметров биологической активности водной экосистемы [1].
Акватория водоема также может рассматриваться как передаточная система, проводящая кислород от атмосферы к донным осадкам. Однако известны случаи образования химических градиентов большой величины на относительно небольших перепадах глубин — в пограничных слоях при относительно небольшой их величине за пределами этих зон. Причина появления таких участков при общей стратификации воды по плотности во всемирном тяготении с одной стороны и радиационном воздействии солнца на воду, приводящего к её нагреванию, с другой. Эти процессы могут привести к снижению скорости продукции, деструкции и рециклинга биогенных элементов и биоорганизмов вплоть до остановки этих процессов, а также предопределять биоразнообразие гидробионтов в целом и видовой состав в частности [2]. Температурная стратификация существенно воздействует на распределение организмов в толще воды, на перенос и осаждение вредных для биоорганизмов примесей. Повышение температуры поверхностных вод приводит к нарушению вертикального водообмена и, соответственно, к уменьшению аэрации глубоководной зоны, снижению растворимости и концентрации кислорода в воде. Стратификация по плотности, температуре и химическому составу ограничивает конвективный подъем в поверхностные слои воды биогенных элементов, углекислоты и продуктов неполного окисления органических веществ, поступающих в гиполимнион (холодные, солёные, плотные слои воды) в результате седиментации (оседания) сестона. С начала стратификации и до момента ее окончания поверхностный слой обедняется, а гиполимнион, напротив, обогащается этими веществами. В результате физико-химическая стратификация приводит к возникновению неравномерного распределения по глубине ряда биологически значимых веществ и является причиной самоорганизации сложной структуры экологических ниш [3]. Математическое моделирование механических, химических и биологических процессов, протекающих в водных экосистемах, чрезвычайно актуально и связано с проблемами экологии и безопасности жизнедеятельности населения прибрежных территорий.
Среди выдающихся ученых, внесших значительный вклад в изучение гидрологии и океанологии, следует отметить В.П. Дымникова, который занимался исследованием климата и океанологии, моделированием атмосферы и океана. А.С. Монин и М.Ю. Белевич исследовали процессы кинематики водной среды, турбулентности и микроструктуры океана. Советский ученый А.С. Судольский занимался исследованием динамики вод и береговых процессов в различных водоемах применительно к решению задач проектирования, строительства и эксплуатации конкретных гидротехнических сооружений или рационального хозяйственного использования водоемов в целом [4]. По мнению В.И. Вернадского, одним из важнейших проявлений жизни является газовый обмен организмов с окружающей средой, главным образом — процессы дыхания, основанные на потреблении кислорода [5]. Изучением гидробиологических процессов водоемов занимались различные выдающиеся отечественные ученые, среди которых С.В. Бруевич, работы которого посвящены разработке аналитических методов исследований, формулировании основ гидро- и биогидрохимии. Г.Г. Матишов и В.Г. Ильичев активно изучают условия оптимальной эксплуатации водных ресурсов, занимаются разработкой моделей транспорта загрязняющих веществ в водоемах и исследованием оценки их воздействия на биоресурсы водной среды [6].
Для изучения влияния перечисленных процессов водной среды разрабатывается комплекс взаимосвязанных математических моделей, основанный на использовании точных прогностических моделей и программной реализации экономичных численных методов, который позволит детально исследовать кинематику процесса, причинно-следственные связи и состояние объекта моделирования. Существующие методы и средства прогнозного моделирования состояния водной среды с учетом ряда биотических и абиотических факторов, включая процессы распределения кислорода, углекислого газа, солей, основаны на общих научных подходах, упрощенных математических моделях, обладающих низкой адаптивностью, отсутствием возможности моделирования нелинейных динамических процессов, свойственных большинству водных экосистем, некорректным заданием границ расчетной области. В некоторых случаях исследования сопровождаются формальным определением граничных условий, дают достаточно грубые и приближенные результаты моделирования.
При моделировании процесса переноса веществ, основанного на уравнениях адвекции-диффузии, необходима хорошая аппроксимация адвективных слагаемых, представляющих собой градиенты давления, плотности массы и полной энергии, импульса движения. Применение стандартных разностных схем при завышенных оценках параметров подобия приводит к потере точности вычислений из-за возрастания погрешности аппроксимации и усилению ограничений на шаг по времени в связи с условием устойчивости разностной схемы. В работах А.И. Сухинова, А.Е. Чистякова и др. [7, 8] показано, как эффективно использовать линейную комбинацию разностных схемам «кабаре» и «крест» с оптимальными значениями весовых коэффициентов для аппроксимации уравнения переноса. Эффективность этих методов достигается оптимизацией погрешности аппроксимации дискретной моделью сплошной среды точного решения задачи переноса вещества с постоянной скоростью. Исследования показали, что такой подход распространяется и на модели гидродинамики с переменной (знакопеременной) скоростью без эффекта сеточной вязкости. Ещё одно положительное качество такого рода аппроксимаций состоит в том, что с их помощью можно моделировать сложные структуры течения, к примеру, вихревые. В настоящее время многие исследователи используют подобные схемы для моделирования турбулентных течений. Сотрудниками ведущих зарубежных научноисследовательских организаций, таких как Stanford University, Imperial College London и др., а также сотрудниками Института вычислительной математики РАН Е.М. Володиным, А.В. Глазуновым, А.С. Грицуном, Н.Г. Яковлевым и др. [9] изданы труды, в которых математическое моделирование климатических изменений, гидродинамических и атмосферных процессов и явлений осуществлено на основе вихреразрешающих схем. Ещё больше снизить требование к шагу по времени и повысить пространственное разрешение модели при ограниченной компьютерной памяти позволяет квазигидродинамическое приближение сплошной среды. На практике в систему уравнений Навье-Стокса и неразрывности добавляется малое слагаемое, пропорциональное второй производной по времени от функции плотности. Данный подход позволяет сгладить нефизические флуктуации плотности массы и импульса, а также полной энергии, переносимые по пространственной сетке быстрее скорости звука.
Существующие универсальные пакеты прикладных программ (например, пакет программ «Mars3d», Экоинтегратор, программный комплекс CHARISMA, комплекс SALMO, комплекс программ CHTDM, CARDINAL, пакеты моделирования различных процессов аэрогидродинамики, программные комплексы PHOENICS, FLUENT, GAS DYNAMICS TOOL) не учитывают некоторые свойства моделируемых сложных систем, снижая таким образом точность и оперативность моделирования. К таким свойствам относятся: пространственная неоднородность движения водной среды, вихревые структуры течений. В математических моделях и в алгоритмах их численной реализации не учитывается вероятность значительного изменения глубины, плотность водной среды, что может привести к неустойчивости полученных численных решений. По этой причине такие специализированные программные пакеты могут быть использованы для моделирования ограниченного разнообразия гидрофизических процессов водных систем. Большая часть известного специализированного программного обеспечения (ADAM, CAL3QHC, Chensi, TASCflow, ISC-3, PANACHE, REMSAD, UAM–IV, ЭКОЛОГ, ПРИЗМА, VITECON), предназначенная для моделирования процесса распространения загрязняющих веществ, взаимодействия гидробионтов, преимущественно ориентирована на однопроцессорные вычислительные системы, представленные, в основном, персональными компьютерами. В таких системах масштабируются на параллельные системы только единичные составляющие модули этих систем (например, ECOSIM и MAQSIP). На практике в систему уравнений Навье-Стокса и неразрывности добавляется малое слагаемое, пропорциональное второй производной по времени от функции плотности. Данный подход позволяет сгладить нефизические флуктуации плотности массы, импульса и полной энергии, переносимые по пространственной сетке быстрее скорости звука.
Материалы и методы. Успешность разработки математической модели гидрофизических и гидробиологических процессов зависит от наличия и проработанности тестовых примеров и задач для изучения устойчиво наблюдаемых в морях явлений, таких как вертикальное перемешивание и перераспределение солёности и кислорода, галоклин и теромоклин. Для изучения этих явлений в работе используется модель гидродинамики, учитывающая баланс массовых сил и трансграничных потоков [1, 2]:
dp + d i t
( V , p v ) = g ,
-
— + (v, V) v = -—Vp + b , dt ( , ) p
p —| k+-^ | = div (Tv) + (v, pb) + (V, h ) + pq ,
Информатика, вычислительная техника и управление
где p v — плотность потока, д k / дt — скорость изменения плотности кинетической энергии, д£ / дt — скорость изменения плотности внутренней энергии, T — тензор напряжений Tn = - рп , b — массовая сила, h = h ( t , x ) — плотность потока тепла, q — удельный приток тепла за счёт излучения. Из-за того, что эти явления обычно описываются вертикальным распределением параметров по глубине, то целесообразно получить упрощённую модель, допускающую оперативную идентификацию ненаблюдаемых параметров. Выделим цилиндрическую область V с основаниями на дне и поверхности воды площадью поперечного сечения S. Спроецируем скорости, потоки и силы на вертикальное направление в предположении, что частные производные по x , y от параметров на горизонтальное направление равны 0 за пределами цилиндра, т.е. предположим горизонтальную однородность параметров водной среды. Запишем систему (1) в консервативной форме так, чтобы она позволила определить плотность массы ( p ), механический импульс ( p v ) и плотность полной энергии (p ( k + e ) ), k = v 2 /2. В цилиндре выделим бесконечно малый объём и предположим, что на каждый такой объём, составляющий V, действуют: сила реакции опоры (дна водоёма), равная гидростатическому давлению, и сила, аналогичная силе трения, вызываемая вязкостью жидкости и переносом импульса, не равная нулю при вертикальных движениях жидкости.
Если пренебрегать горизонтальными перемещениями жидкости и предположить, что существенны только вертикальные движения, и тот факт, что плотность водной среды существенно зависит от солёности, принять изложенные ранее упрощения и соглашения, то уравнения гидромеханики [1–3] в компактной форме представимы системой дифференциальных уравнений в частных производных [2]:
* + « = 0, д t
i ( p v )d( p v 2 ) дP^p,SJ7 - д( I v 1
-
' +a - + F / 5 , F = - p gS -^l Ц^ I, p = f (p, T )
д t дx дx дx V дx )
-
— Fp(e + v2 / 2)1+ —Гv(p(e + v2 / 2))1 = —(P—) + — + —fk —)- k(T - Tm„), T = f (e) = £ / c(1)
д tL J дxL ( )J дx 5 дx( дx) V envv
дs д(vs) д f дs 1
— ■ I Ц— I,
д t дx дx V дx )
где p = f (p, T, s), £ = f (p, v, T) — эмпирическое уравнение состояния морской воды и уравнение, замыкающее систему по внутренней энергии соответственно; р — полное гидродинамическое давление; p — локальная плотность водной среды; v — проекция вектор-функции скорости на вертикаль (ось z направлена вверх от дна к поверхности); £ — объемная плотность внутренней энергии; р — давление газа, заключённого в элементарном объеме между соседними слоями; F — объемная плотность обобщённой силы (суммы сил), приложенных к элементарным объёмам жидкости, помимо давления; s = s (x,t) — концентрация соли; 5 — площадь поперечного сечения цилиндрической выделенной области, в которой предполагается наиболее интенсивное протекание процесса апвеллинга и транспорта соли; T — абсолютная температура воды; T — температура воды внешней по отношению к выделенному объёму; k — теплопроводность воды;
g = 9,8м / с2 — ускорение силы тяжести; ц — коэффициент, характеризующий интенсивность переноса импульса из-за вязкости.
Граничные условия, характеризующие свойство непротекания жидкости через породу, составляющую дно водного объекта, для системы (1) могут быть записаны в виде равенств:
( v ,n ) = 0, | P = 0, I T = 0, I s = 0. (2)
д п д п д п
Где n — вектор нормали, направленный внутрь расчётной области.
Международный стандарт уравнения состояния морской воды [10] определяет плотность р морской воды как функцию солености s , температуры T и гидростатического давления p , которая имеет вид:
Р ( 5 , Т , Р ) =
P( 5 , T ,0)
1 - p / K ( 5 , Т , p ) ,
где K(s, T, p) — средний модуль упругости; цифра 0 соответствует одной стандартной атмосфере (101 325 Па).
При численном моделировании на основе (1) - (3), также востребованной как (3), установим алгебраическую связь давления с плотностью, температурой и солёностью. Квадратное уравнение имеет два корня:
_ ±V D + ( 1 - A ) -р ( 5 , Т , p ) + A • p о ( 5 , Т , p )
p 1,2 л , (4)
DN
D n = 2 B ^ ( р ( 5 , Т , p ) -Р о ( 5 , Т , p ) )
D = (-4 BK о ( 5 , Т , p ) + A 2 - 2 A +1) • р( 5 , Т , p ) 2 + (8 B • K 0( 5 , Т , p ) - 2 A 2 + 2 A ) • p 0( 5 , Т , p ) • (5)
•р(5,Т, p) + (A2 - 4B • Kо (5, Т, p)) • pо (5, Т, p)2, где A , B , p0 (5, Т, p ), Ko (5, Т, p) — переменные параметры, связь которых с температурой, солёностью и плотностью определена стандартной моделью морской воды; р(5, Т, p) = р , где Т — температура воды в градусах Цельсия. Скорость звука в солёной воде может
быть выражена формулой: c ( 5 , Т , p ) = ^д p / др .
Предположим, что импульс, солёность и теплота объёма воды, ограниченного цилиндрической поверхностью, меняются только при изменении параметров на границе области (граничные условия Дирихле), в частности, изменении солёности на поверхности воды. Поведение механических параметров — плотности, импульса — задано условиями Неймана и внешнему воздействию недоступно. Независимо от этих допущений, внутри границы водной среды система уравнений (1) может быть записана в векторной форме модели переноса-реакции с источниковой добавкой [11, 5]:
d q + f =7 д t д x '
где Т = ( 0 F/S + тх Fv/S + к д 2 Т /д x 2 - к ( Т - Тт г)) т — вектор, характеризующий взаимодействие потока с окружающей его жидкостью и планетой; q = ( q р v E )т — вектор консервативных переменных состояния; f = ( р v p + р v 2 v ( E + p ) ) — вектор потоков, выполняющих роль обратной связи и замыкающих уравнение баланса. Из компонент вектора f можно вынести общий множитель f = v • q .
На практике для решения уравнения переноса вида (6) хорошо себя зарекомендовала разностная схема, оператор послойного перехода которой получается линейным комбинированием аналогичных операторов перехода схем «кабаре» и «крест» [12-15]. Учет связи потоков массы и изменения плотности оказался более эффективным по регуляризованной по Б. Н Четверушкину квазигидродинамичекой системе, аппроксимированной по схеме ВВЦП (разности со сдвигом вперёд и центральные по пространству).
Дискретизацию модели сплошной среды будем проводить интегро-интерполяционным методом на равномерной сетке S = S , х S2 St = { x = ih , i = 0+ n , n • h = L } , S2 = { t j = j т, j = 0^ m , m -т = Т } , где h — шаг сетки по вертикали, i — индекс узла (контрольного/конечного объёма в терминах метода Годунова) при нумерации по пространству, т — шаг сетки по времени, j — номер временного слоя. Опишем конечноразностную аппроксимацию модели (1). Разностные схемы, используемые для аппроксимации уравнений баланса первого порядка, дают сравнительно приемлемые результаты лишь при очень малом шаге сетки [3], что приводит к активному потреблению ресурсов вычислительных устройств и разработчиков, создающих алгоритмы и программы.
Проблема постановки граничных условий и их согласованного задания при знакопеременной скорости решалась методом заполненности контрольных ячеек [7]. Учет максимальной заполненности и выражение её функциональной зависимостью от номера узла позволяет повысить точность аппроксимации граничных условий.
Работа по теоретическому и экспериментальному подбору методов и схем аппроксимации привела к выбору методов расщепления [13] и регуляризации. Уравнения неразрывности регуляризируется по Б.Н. Четверушкину. Данное уравнение подвергается разностной аппроксимации по схеме ВВЦП. Уравнения баланса (переноса) импульса, солёности и полной энергии заменяются явными уравнениями, полученными линейным комбинированием различных аппроксимаций оператора переноса («чехарда» и «кабаре») [12, 15]. В соответствии с методом расщепления, перенос импульса (и скорости), солёности, полной энергии
Информатика, вычислительная техника и управление
аппроксимирован на дробном шаге. Изменение скорости движения воды, определяющей интенсивность переноса массы вещества, вводится на втором дробном шаге решением волнового уравнения. Обозначим p = p^, p = p
n
+a
, p = p
n
+1
,
v
=
vn
,
v
=
v
n
+G
,
v
=
v
n
+1
, 0
|
записаны в виде: |
p v — p v ' д f д v ) + v -( p v X = p gS ( x ) . 1 ^. 1 , (7) т д x V д x J o-o n +1- 7P^-nP^ —1 -1 ^ i -^ i - + ( p v X 1 = P xx — I -^------ 2i2 i 1, p = f ( p, T ) , c = c ( 5 , T , p ) , (8) x т< т J V c 2 т 2 J = — pv (9) т |
Уравнения (7) и (9) представляют собой дискретный аналог модели переноса и изменения импульса — второе уравнение системы (1). Уравнение (8) прогнозирует изменение поля давления при учёте неразрывности потока и информации о межузловых (межъячеечных) и граничных потоках. При допущении постоянности по времени на каждом шаге скорости звука уравнение (8) может аппроксимироваться неявной разностной схемой по времени и решаться прогонкой. Именно это направление в численном моделировании и было выбрано для исследования.
Уравнение (7) и четвёртое уравнение (1) аппроксимируем на эквидистантной сетке явной разностной схемой [13]. Слагаемые (8), определяющие волновые свойства при распространении импульса (правая часть уравнения), аппроксимируем центральными разностями по пространству:
Оставшиеся два слагаемых (8) определяют связь скорости изменения плотности с её потоком. В (8) входит отношение скорости изменения плотности к отрезку времени т, выражаемой разностью со сдвигом вперёд: p n+1-p n k 0,i т 2 , поток массы переносится в правую часть (8) и аппроксимируется центральными разностями:
1 a ( p u )
0,1 т дx
. (( pu) i+1/2 — ( pu) i ).. (( pu) i — ( pu) i—1/2 )
k l ■ + k ■
1,i 2,i h•т Нч
x xi где k , k , k — степень заполненности областей, находящихся в окрестности ячеек c номером i [7]; k характеризует заполненность области [x,x] ; k — [x,x] , k — [x,x] .
Уравнения баланса механического импульса и давления (9) аппроксимируем ВВЦП:
pu n+1 — pu n+1/2 k 0, i
т
—
П+1
k^
—
2h
уП + 1
+ к
Р Г+1 — P “-+1
2,i 2h
.
Представим задачу разрешения разностной аппроксимации уравнения (8) в форме задачи матричной прогонки с переменным во времени вектором в правой части Ax = F :
Ax. i + Cx + Btxi+ 1 = F .
Аппроксимация уравнения (8), определённая на трёхточечным разностном шаблоне, в форме линейной системы уравнений Ap n + 1 = f ( p n , p n — 1 , ( p v ) ) , разрешаемой относительно давления (p), имеет вид:
|
f 1 1 _ + . 2c 2 t 2 h2 1 — h 2 |
1 h 2 12 --1-- c 2 T2 h 2 |
0 1 — h 2 |
|
0 |
1121 |
|
|
h 2 c 2 T 2 h 2 ,h 2 |
||
|
0 |
||
|
0 |
0 - Y |
|
|
h 2 |
||
|
0 |
||
|
V |
|
0 |
|||||
|
0 |
( n u + 1 A p 0 |
||||
|
0 |
P 0 -+ 11 P U +1 p -U + i1 |
||||
|
1 --+ c 2 T 2 1 |
2 h 2 |
1 — h 2 1 |
1 |
V P N +1 J |
|
|
- h2 |
2c 2 t 2 |
h 2 J |
|||
f 1 1 1
= |ттт(2 p 0 - p 0 ) ...... ~’(2 PU - PU-1) ...... 7TT'(2 PN - PN)
V2c2t2 c2t2 2c2t2
+ 1 (( p 0 -P o ) /2 ...... p i - P i ...... ( p N - P N ) /2 ) T +
+ 7^ ( (p v ) 1 ...... (p v L -(p v ). - 1 ...... -(p v ) n - 1 У .
Подобная ленточная матрица получается в ходе аналогичной аппроксимации двух других слагаемых (8).
В модели могут быть учтены динамические изменения потока на границах и других параметров, таких как температура, солёность, кислородосодержание. Поэтому моделирование движения воды нужно выполнять в цикле по времени послойно с удержанием оперативной информации о параметрах как минимум на двух соседних по времени слоях решения сеточного уравнения. Алгоритм вычисления гидродинамических параметров на двухиндексной сетке по пространству и времени включает в себя:
-
- построение прогноза изменения импульса по первому уравнению (7);
-
- приближённое вычисление функции пространственного распределения давления как функции плотности и температуры с предыдущего временного слоя;
-
- оценку изменения плотности по второму уравнению (8);
-
- вычисление градиента давления по новым значениям плотности и температуры, корректировка распределения импульса по третьему уравнению (9);
-
- нахождение нового распределения полной энергии и температуры по аппроксимированному третьему уравнению системы (1).
При алгоритмизации метода решения системы расщеплённых уравнений введены:
- двоично-числовые маски, предопределяющие переключение шаблона разностной схемы с изменением знака скорости;
- переменные сдвиги индексов соседних узлов, позволяющие записать решение уравнения (12) для граничных и внутренних узлов единой системой вычислительных операций.
Такие переменные сдвиги индексов используются при вычислениях аппроксимаций градиентов как в объёме модели сплошной среды, так и на границах со вторым порядком точности по дискретным аналогам уравнений (7)–(9), аппроксимированных по ВВЦП и по линейной комбинации схем «чехарда» и «кабаре»
(CABARET) [12–14]:
q U +1 - q U 4 f qU, - q U -1 q U - q U , ^ q U - q U -1 q n . + q n.
±1______±L_ + i 1 1 1 + yU 1 i-1 1 + 1 __+ yU “1+1 i-1 1 = 0 yU>
T 3 V 2t i h J 3t 1 3h , 1 ",
q n +1 - q n + 4 f q ^ - q ^1 + v n ^ ^ - q n |+ q n - q n -1 + v n q kz q k= 0 v. < 0
T 3V 2t i h J 3t i 3h ’ i, где характеристика q для переноса соли (q = s ) и импульса q = pu .
Параметр m представляет собой «переключатель» потока при изменении знака скорости в разностных аппроксимациях градиентов давления и потока массы:
0, y < 0, m = 1 - m , m = 1 1’ y > 0,
При использовании такого переключателя аппроксимация градиента при решении задачи переноса для импульса и солёности может быть записана формулой:
Информатика, вычислительная техника и управление
d q _ 2 f m q i - q , -1 +- q i + 1 - q i Y1 q i +1 - q , -1
ax „ ~ 3 V h h J 3 2 h x xi
Применение метода заполненности ячеек позволяет корректно аппроксимировать граничные условия при размещении параметров состояния воды в памяти компьютера массивом числовых значений, а переменные сдвиги индексов позволяют уменьшить объём символьной записи подпрограммы выполнения послойного итерационного изменения переменных состояния, отнесённых к узлам разностной схемы [17].
Матричное уравнение с ленточной трёхдиагональной матрицей A (13) решается прогонкой [18]. Для начальной верификации программной реализации использовалась упрощённая модель состояния солёной воды в виде уравнения П. С. Линейкина.
Результаты исследования. Моделирование выполнялось на основе программного комплекса, написанного на языке Matlab. Отладка проводилась с использованием интерпретатора GNU Octave. Эксплуатация также предполагает наличие библиотек этой системы. Программный комплекс состоит из 16-ти функциональных модулей. Выбор этого интерпретатора и соответствующего языка обусловлен возможностью записать и проверить программу, оперирующую с массивом переменных состояния, являющегося проекцией искомых функций ρ( x , t ) , v ( x , t ) , ε( x , t ) на пространственную сетку. На этом этапе исследования авторы абстрагировались от специфики выполнения поэлементных операций над массивами действительных чисел.
Программная система состоит из взаимосвязанных подпрограмм:
-
- выполнение одного шага по уравнению переноса по формулам (10);
-
- расчет плотности морской воды (unesco_urs);
-
- расчет давления морской воды, находящейся в поле силы тяжести, при заданной температуре, солёности и плотности по эмпирическим уравнениям состояния (rhoTS2P);
-
- вычисление скорости звука в зависимости от температуры, солености и давления по стандарту и уточнённой формуле «ЮНЕСКО» (speed_of_sound);
-
- оценка величины силы вязкости жидкости при движении её объёмов под действием сил давления во всех точках пространственной стеки (ForceOfFriction);
-
- циклическое варьирование переменных состояния и времени при вертикальном движении солёной воды (aqua_process);
-
- начальная установка константных величин, характеризующих жидкость, начальные и граничные условия её глобального гидрофизического равновесия (start, set_parameters);
-
- формирование ленточной матрицы, аппроксимирующей уравнение, содержащее давление (func5);
-
- решение матричного уравнения методом прогонки (run_sweep_shuttle);
-
- преобразование температура ↔ полная энергия (TFromE, EFromT);
-
- расчет баланса полной энергии (TotalPower);
-
- решение задачи диффузии-конвекции-реакции, в том числе при аппроксимации комбинации разностных схем «чехарда» и «кабаре» (ADR_solver);
-
- оценка величин градиентов и производных по времени по центральным и направленным разностям с учётом изменения знака скорости и шаблона разностной схемы (diff123).
Построенная модель использована в тестовом запуске для оценки изменения плотности при повышении солёности поверхности водной среды на 1‰ на 30-й секунде от начала моделирования и максимальной глубине 1 км. Переходные процессы по плотности во множестве отстоящих друг от друга сечений (функция ρ(t, x) ), вызванных мгновенным изменением концентрации соли, конечны во времени (рис. 1), а x∈S1
фронт импульса плотности сильно ослабляется при движении в пространстве.
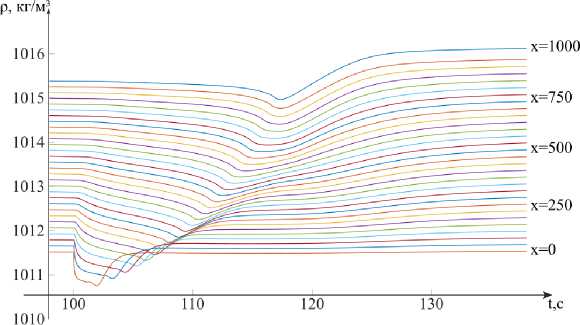
Рис. 1. График зависимости плотности от времени при резком изменении солёности на поверхности воды
Обсуждение и заключение. Представленная пространственно-распределённая модель пока не позволяет прогнозировать устойчивое перераспределение плотности и изменение градиента солёности при численных расчетах, потому что в ней не учтена плавучесть менее солёной воды и её изменение при осолонении верхних слоёв. Математическое и программное обеспечение, значительно упрощающее моделирование процессов, приводящих к наблюдаемым эффектам галоклина, хемоклина и пикоклина, проверено и отлажено на множестве тестовых задач (транспорт импульса, соли, распространение волны давления). Для высокоточного моделирования наблюдаемых физико-химических явлений в морях понадобится решать дополнительные задачи идентификации параметров модели, взяв в качестве исходной информации данные наблюдений и дистанционного зондирования Земли.
Список литературы Моделирование вертикальных движений морской воды в стратифицированных водоемах
- Михайлов В.Н., Добровольский А.Д., Добролюбов С.А. Гидрология. 2-е изд., испр. Москва: Высшая школа, 2007. 464 с. URL: https://www.geokniga.org/bookfiles/geokniga-mihaYlov-vn-dobrovolskiY-ad-gidrologiYa-2007.pdf (дата обращения: 01.04.2023).
- Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах. Монография. Москва: Физматлит; 2008. 231 с. URL: https://www.evolbiol.ru/docs/docs/large files/ilyichev.pdf (дата обращения: 01.04.2023).
- Богданов Н.И. Биологическая реабилитация водоемов. Пенза: РИО ПГСХА; 2008. 126 с. URL: https://microalgae.ru/f/bogdanov na biologicheskaya reabilitaciya vodoemov 2008.pdf (дата обращения: 01.04.2023).
- Судольский А.С. Динамические явления в водоемах. Ленинград: Гидрометиоиздат; 1991. 260 c. URL: http://elib.rshu.ru/files books/pdf/img-217140610.pdf (дата обращения: 01.04.2023).
- Геворкьян В.Х. Литологические аспекты учения В. И. Вернадского о биосфере. Геология и полезные ископаемые Мирового океана. 2010;3(21):37-56. URL: https://core.ac.uk/download/38371310.pdf (дата обращения: 01.04.2023).
- Il'ichev V.G., Rokhlin D.B. Internal Prices and Optimal Exploitation of Natural Resources. Mathematics. 2022;10(11):1860. https://doi.org/10.3390/math10111860
- Sukhinov A.I., Chistyakov A.E., Belova Yu.V., et al. Supercomputer Modeling of Hydrochemical Condition of Shallow Waters in Summer Taking into Account the Influence of the Environment. Communications in Computer and Information Science. 2018;910:336-351. https://doi.org/10.1007/978-3-319-99673-8 24
- Nikitina A.V., Kravchenko L., Semenov I.S., et al. Modeling of Production and Destruction Processes in Coastal Systems on a Supercomputer. MATEC Web of Conference. 2018;226:04025. https://doi.org/10.1051/matecconf/201822604025
- Iakovlev N.G., Volodin E.M., Gritsun A.S. Simulation of the Spatiotemporal Variability of the World Ocean Sea Surface Height by the INM Climate Models. Atmospheric and Oceanic Physics. 2016;52(4):376-385. https://doi.org/10.1134/S0001433816040125
- Mcdougall T.J., Millero F.J., Feistel R., et al. The International Thermodynamic Equation of Seawater - 2010: Calculation and Use of Thermodynamic Properties. Paris: UNESCO; 2010. 196 p.
- Кудинов Н.В., Нейдорф Р.А., Журавлёв Л.А., и др. Использование пакета Simulink для опорно-параметрического я моделирования переходных процессов на участке магистрального газопровода. Вестник Донского государственного ^ технического университета. 2012;12(1-2):60-66. URL: https://www.vestnik-donstu.ru/jour/article/view/498 (дата ^ обращения: 02.02.2023). ^
- Сухинов А.И., Чистяков А.Е., Проценко Е.А. Разностная схема для решения задач гидродинамики при больших сеточных числах Пекле. Компьютерные исследования и моделирование. 2019;11(5):833-848. и https://doi.org/10.20537/2076-7633-2019-11-5-833-848 %
- Сухинов А.И., Чистяков А.Е., Проценко Е.А., и др. Линейная комбинация схем «кабаре» и «крест» с g весовыми коэффициентами, полученными из условия минимизации порядка погрешности аппроксимации. ьл Чебышевский сборник. 2020;21(4):243-256. https://doi.org/10.22405/2226-8383-2020-21-4-243-256 g
- Сухинов А.И., Белова Ю.В., Чистяков А. Е. Моделирование биогеохимических циклов в прибрежных g системах Юга России. Математическое моделирование. 2021;33(3):20-38. https://doi.org/10.20948/mm-2021-03-02
- Сухинов А.И., Чистяков А.Е., Проценко Е.А. О разностных схемах кабаре и крест. Вычислительные методы и программирование. 2019;20:170-181. https://doi.org/10.26089/NumMet.v20r216 s
- Гущин В.А. Разработка и применение метода расщепления по физическим факторам для исследования течений несжимаемой жидкости. Компьютерные исследования и моделирование. 2022;14(4):715-739. https://doi.org/10.20537/2076-7633-2022-14-4-715-739
- Кудинов Н.В., Никитина А.В. Компьютерные модели осесимметричного движения газа по каналам для решения технических и естественно-научных задач. В: Интеллектуальные информационные технологии и математическое моделирование: Труды Международной научной конференции Интеллектуальные информационные технологии и математическое моделирование (ИИТ&ММ-2022). Дивноморское, Краснодарский край; Донской государственный технический университет ДГТУ; 2022. С. 93-100.
- Sukhinov A.I., Chistyakov A.E., Nikitina A.V., et al. A Method of Solving Grid Equations for Hydrodynamic Problems in Flat Areas. Mathematical Models and Computer Simulations. 2023;35(3):35-58. https://doi.org/10.20948/mm-2023-03-03


