Моделирование виброакустической динамики рельса на шпалах

Введение. При установке рельса на шпалах он может быть представлен как система двухопер-тых источников, одновременно излучающих звуковую энергию, а каждый участок рельса между шпалами — как линейный источник ограниченной длины. Экспериментальные исследования показали, что спектр звукового излучения и вибрации рельса имеет высокочастотный характер. Можно предположить, что для уточнения закономерностей шумообразования длина источника соот ветствует длине участка рельса между шпалами.

Основная часть. Для такой модели на основе работ [1, 2] применительно к конструктивным па раметрам рельса получены следующие выражения звукового давления: f.Bh,            /           Зп/ , ,      „ „

Р = 0,1 ^ ^р cos Рехр/ \k₀R +ср - — , при k_oh_p cosp <1;

B(f_kh_D cosp)^0,5 ,                     .

P = 76 ——^----—exp i (k0R + kohp cos P - 2п), при kQhp cos P > 1, где р — угол излучения; fk — собственные частоты колебаний, Гц; В — функция, учитывающая амплитудно-фазовое распределение виброскорости на поверхности рельса и по данным работы [1] определяемое зависимостью

1     /

В = (z)exp(-*_ozsinp)t/z.

V2n о

В данном случае виброскорости определяются из системы дифференциальных уравнений (при условии, что на участке между шпалами действует силовое воздействие только от одного колеса):

ej_x — т-рЛ —Ат + рР—у = A6(z-z₀;

х az4 х az2at2 at2 у v °’

a4s 7 а4е с a2s              х

EL — —5—т + Р^— т = ^РЛ(² -Zn).

у az4 у az^at7 at7 х k 07

Для условий крепления рельса к деревянным шпалам изгибная жёсткость сравнима с жёсткостью опоры. Этот вариант соответствует шарнирному закреплению и в соответствии с краевыми условиями система уравнений (4) примет вид:

а4^    7 а4^ сд2^ 2Р ” . пАгИ . nAz

EL — у-рЛ—у^ + рЛ — y = — sin——fsin——;

х az4 х az^ae at7 I h /       /

„₇ 5⁴e     ₇ a⁴E _ d²s 2P_x . nAri/ . . nAz

EL —у-рЛ 5—y + p/⁷ т = ~АУ sin——fsin——.

y az4 y az2at2 at I ^     /        /

Выполняя аналогичные преобразования, получим:

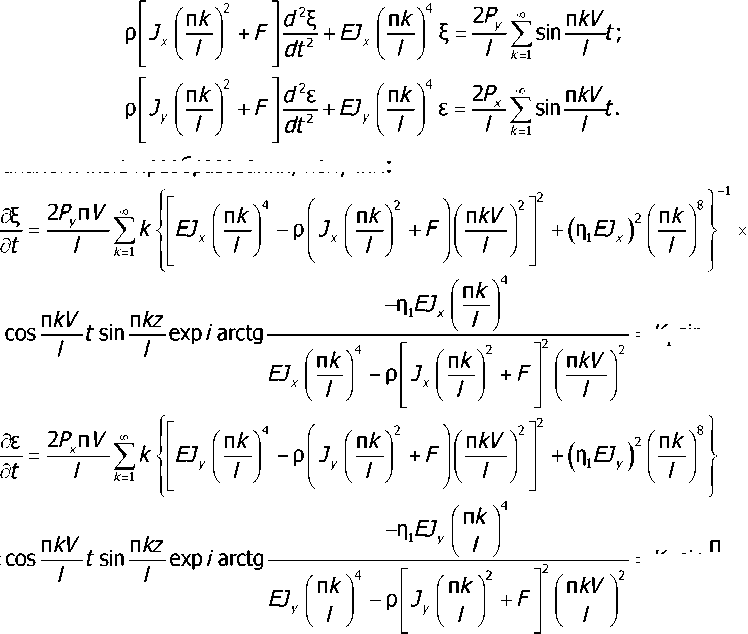
„ . nAz

= K_t sin —^—;

= /<2sin-p.

Выполняя аналогичные преобразования, получим:

В этом случае функция В, определяющая амплитудно-фазовое распределение виброскорости на поверхности рельса, определяется выражением:

Г._п2 п/c-ysinp _gin2 п/с + /г₀/ sin (3

2п

H^-^sinp

H^ + ^sinp

Для варианта установки рельсов на железобетонные шпалы, изгибная жёсткость межопорной части меньше жёсткости опор. В этом случае целесообразно применить модель жёстко защемлённой балки или оболочки. Краевые условия будут иметь вид [3]:

z=0,              z=/, у = 0, — = 0, У = о, — = 0.

az                  ay

Функцию, удовлетворяющую краевым условиям, зададим в виде:

/ х . зnAz ip(z) = sin3—,

• ,, х              nAz . з пА1/ .

тогда 6(z-z_n) = -> sin³——sin³— —t.

/ k=l '              '

Уравнения изгибных колебаний примут вид:

54   ₇ 34 _с 8^ 2Р” . ₃ nAV, . з nAz

EJ_Y — — рЛ—+     = —sin³ —— Г sin³ ——;

х 8z4 х 8z28t2      8t2    1 П /         /

5⁴е     ₇    5⁴е _г 5²е 2Р_Х . з пА1/ . . з nAz

E3_V —г-РЛ—5—т + Р^— т = — sin³—— fsin³——.

• ^у az^{4 у} az²at² at² м

Используя известную формулу sin3x = 3(3sinx-sin3x) и принцип разделения переменных, получим систему дифференциальных уравнений:

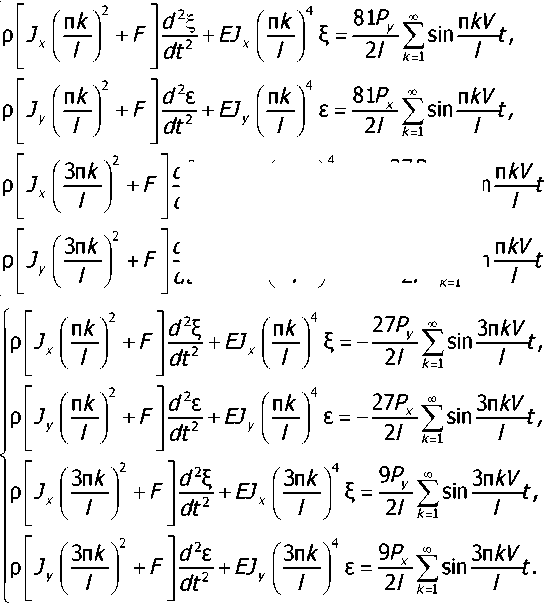
Решение данной системы относительно виброскоростей получено в следующем виде:

dt2 x	f ЗпА- У , _	27^ 2/	Af=l
й2г       , dt2 +EJy\	ГЗпА-V _	27 Px 2/	•£sin Af=l

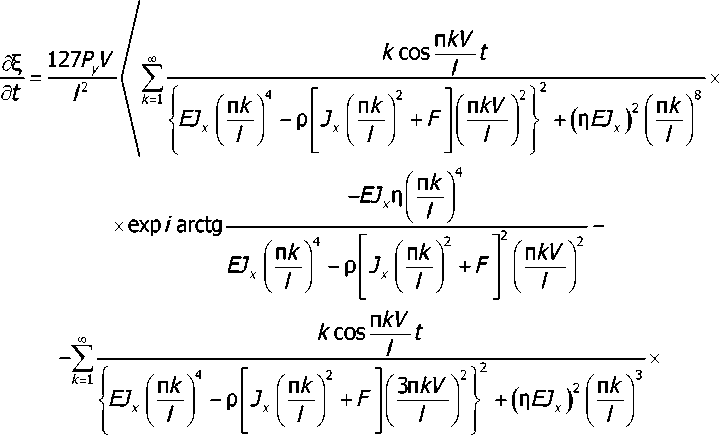
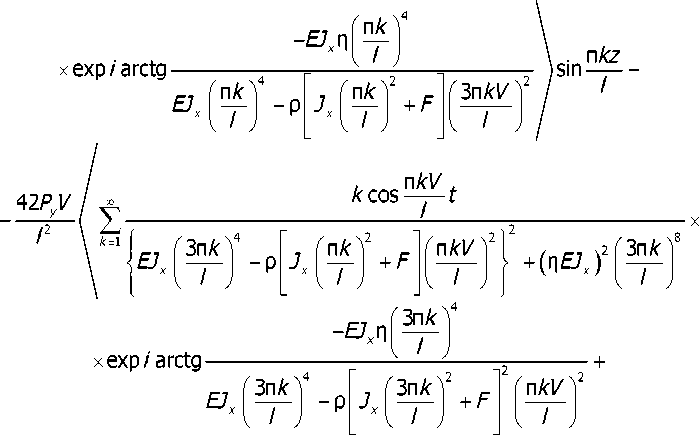
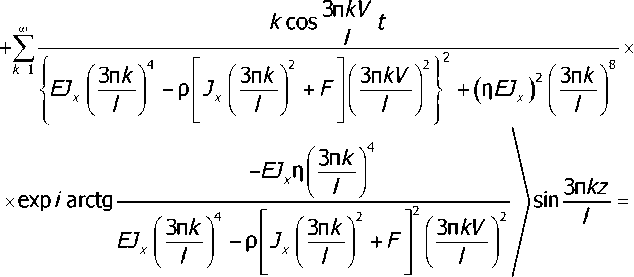
., . nAz ,, . 3nAz = /С₃ sin —— + К₄ sin——

(Ю)

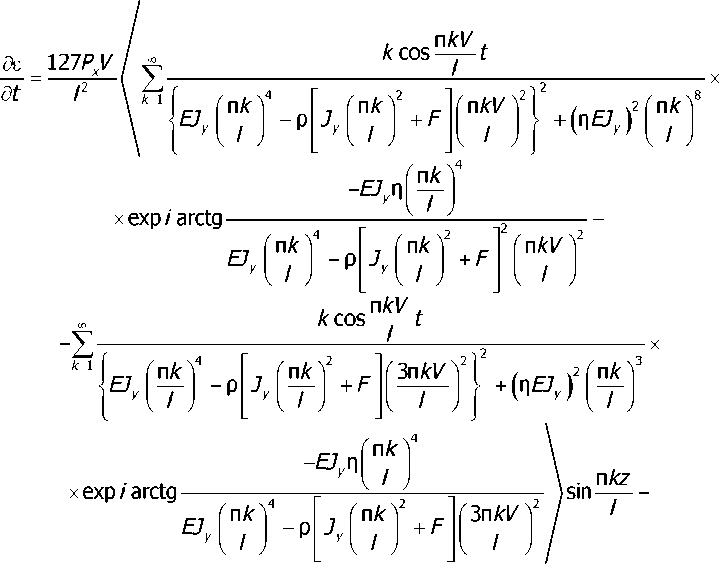
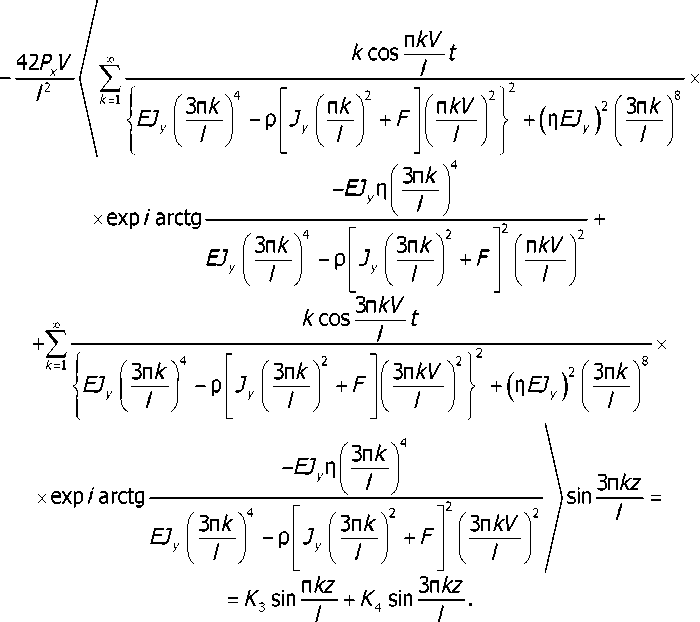
Функция, определяющая амплитудно-фазовое распределение виброскорости на поверхности рельса, определяется выражением:

Зтах^

4тах^

. 2 nA'-/c1/sin|3

sin2-------9------

^-/CoSinp

. 2 nA' + /cn/sinB) sin2-------9------

H^ + ZCoSinp

( . , 3nA'-/cJsin|3

sin2--------9------

. 2 3nA' + /cn/sinB) sin2--------9------

(И)

3n/c , . _o —Г -^smp

3n/c , . o —+ /cosinp

Заключение. Полученные результаты звукового излучения рельса существенно уточняют закономерности шумообразования и объясняют причину высокочастотного состава спектра шума рельса. Кроме этого, учёт диссипативной функции, задаваемой эффективным коэффициентом потерь колебательной энергии, позволяет обосновать выбор материалов вибродемпфирующих покрытий шейки рельса, обеспечивающих снижение шума в самом источнике его возникновения.