Моделирование виброакустической динамики рельса на участке пути с балластным слоем

Введение. В качестве модели рельса как источника звука принят линейный источник. Теоретически рельс представляет собой волновод бесконечной длины. Для инженерных расчётов шумо-образования следует учитывать конечный участок. Он излучает звук, который вносит определяющий вклад в акустическое воздействие на окружающую среду и на внутренние воздушные объёмы кабин локомотивов и вагонов.

Основная часть. Экспериментальные исследования показали: для технических расчётов акустических характеристик длина «главного» излучения звуковой энергии с рельсом составляет 1,1+1,2 от длины состава.

В качестве исходной зависимости принимается формула звукового давления протяжённого линейного источника [1, 2], которая для конструктивных параметров рельса приведена к виду

Р (/?,ф) =/3381/,

exp/^ + ^--J

Mv (k h llr О ' п \К0Пр)^К0К

где V_r— скорость колебаний рельса, м/с; Аь — волновое число, 1/м; R — расстояние от рельса до расчётной точки, м; h_p — высота рельса, м; H^Y — производная функции Ганкеля.

Данная зависимость верна при kQhp»l, что справедливо для высокочастотной части спектра, т. е. частотного диапазона, характерного для спектра шума, излучаемого рельсом. Заменяя производную функции Ганкеля её асимптотическим представлением для kohp >1 [3]

^М(^Р) = -/ К^ехр/4д

^||АО//Р V           ~     / и учитывая, что колеблется твёрдое тело (тм = 1), получим выражение звукового давления, излучаемого рельсом:

Р_р = 4231/, ^ ехр / (k₀R - k_oh_p + ср).

В области средних частот выполняется соотношение k_Qh_p <1. В этом случае асимптотическое представление функции Ганкеля имеет вид [3]

п<кЛ)

Звуковое давление, создаваемое рельсом в этом частотном диапазоне, определяется следующей зависимостью:

Г'⁵ь² Р_в = 0,21/ —ехр / 'JR

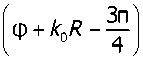
Виброскорости рельса определим из дифференциальных уравнений поперечных колебаний:

+    + j^ = PvyMz-zA х ах4 х az^at7 at2              v ’

„ 54E    7   54£                              x

EJV—Г-РЛ—5—т + pF—- + J£ = px> 5(z-zn,Y v axA v az2at2 at2 хй v 0,7

где 5(z-z0/) - дельта-функция, характеризующая силовое воздействие на колесо; к* — количество колёсных пар.

где /?, —расстояние от оси первой колёсной пары до оси следующей, м.

Учитывая, что вибрации рельса возбуждаются силовым воздействием со стороны подвижного состава, и используя метод разделения переменных (метод Фурье), получим следующие системы дифференциальных уравнений:

2Р -=

/к к=1

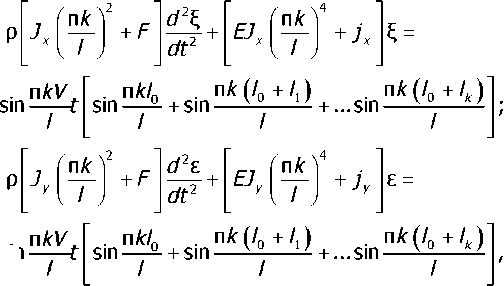
2Р -

= —^У sin

/К ^=1

где 1/— скорость движения состава, м/с; к — коэффициент, характеризующий соответствующую моду собственных колебаний рельса.

Решение уравнений колебаний рельса относительно виброскорости в направлении осей координат ОХ и ОКимеет следующий вид:

2пР kV

55 dt

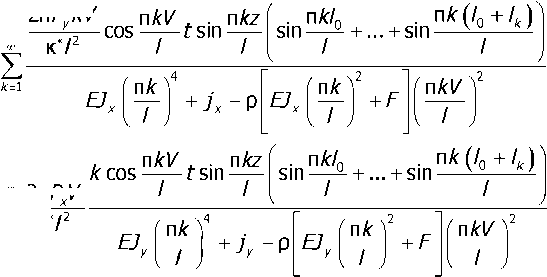
. x\kz sm——;

. nkz sin-----.

5е _^2пРУ

Для теоретических расчётов спектров шума целесообразно амплитудное максимальное значение среднеквадратичной виброскорости, т. е.

\х /max \ /max

Таким образом, полученные зависимости позволяют определить создаваемое рельсом звуковое давление и его уровни на каждой собственной частоте колебаний в зависимости от геометрических, механических параметров, скорости движения локомотива. Для расчёта звукового давления по формуле (2) частота колебаний рельса фактически задаётся коэффициентом к, т. е. для первой собственной моды к= 1, для второй к= 2 и т. д. В формулу (4) непосредственно входит частота собственных колебаний, и для её определения воспользуемся данными работы В. 3. Власова [4]. Частоты собственных колебаний находим из уравнения свободных колебаний:

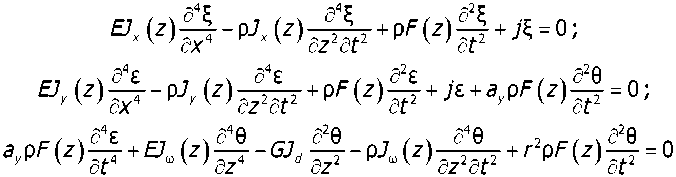
Первое из выражений (9) содержит лишь частные производные функции ^z,t^ и представляет собой уравнение изгибных вынужденных колебаний. Второе и третье выражения образуют систему дифференциальных уравнений и определяют совместно с граничными условиями пространственные изгибно-крутильные колебания. Соотношения жёсткостей заготовок и опор заданы таковыми, что последние могут рассматриваться как шарнирные. При таком допущении граничные условия имеют вид:

при z = O,s = 5 = 0 = 0;

5²е _ д²5 _ д²6

при z = /, s = 5 = 0 = 0;

5z2

52e

5z2

5z2 5z2

= 0,

5^5 = 5^6 =п

5z2 5z2    "

(Ю)

Решение системы (9) представлено следующим образом: s(z,f) = j^s^sinA^z,

^,t)=ES(t)sinVz

(И)

O(z,f) = ^9(f)sin A/(z.

п к к = — (к = 1, 2, 3,...).

= 0,

В результате подстановки выражения (11) в систему (9) получены следующие уравнения:

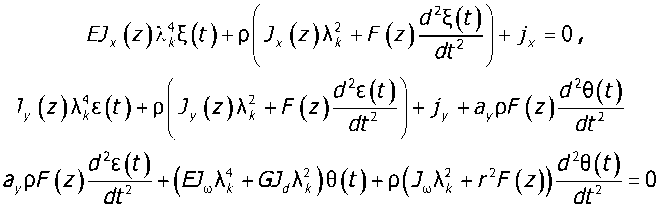
Общее решение однородных уравнений (12) получено в виде простых гармонических колебаний:

^(t) = -4* sin^f, г^=В* s\x\k_kt, 0(f) =С* sin^f.

Тогда система (12) принимает следующий вид:

-a,pF (z)^B-+[£7.(z)A; + GJ. (z)A= -p(j. (z)A? (z)^)Jr =0.

Частоты собственных колебаний получим, приравнивая к нулю определитель системы уравнений (14), составленный из коэффициентов /Г, в', С*.

Каждому значению, характеризующему форму колебаний, соответствуют три частоты свободных колебаний kia, кю., к^. Первая частота соответствует изгибным колебаниям, вторая и третья — сложным изгибно-крутильным колебаниям.

Фактически расчёт виброакустических характеристик на каждой собственной частоте колебаний и даёт возможность теоретического определения спектров вибрации и шума (октавных или третьоктавных). Для этого расчётные уровни звукового давления энергетически суммируются по соответствующим полосам октавных или третьоктавных диапазонов. Чтобы выбрать наиболее рациональный вариант систем шумовиброзащиты, необходимо сравнить полученные уровни с предельно допустимыми и выделить частотные области, в которых вибрация и шум превышают санитарные нормы.

Как видно из полученных зависимостей, реально снизить шум и вибрацию рельса можно только изменяя его диссипативные свойства, в том числе у основания рельса. Фактически диссипативные свойства рельса и основания не учтены в зависимостях виброскоростей и, следовательно, звукового давления. Для этого воспользуемся известным приёмом и представим модуль упругости и жёсткость основания в комплексной форме [5]

где Hi и Пг — эффективные коэффициенты потерь колебательной энергии рельса и подрельсового основания.

В этом случае после преобразований получим

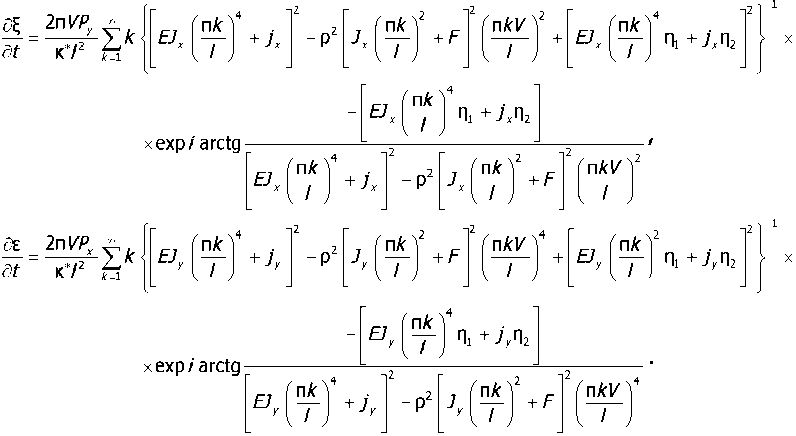
Заключение. Полученные зависимости скоростей колебаний подставляются в формулу (4) и таким образом определяются спектры шума. Эти данные являются базовыми для расчёта спектров шума на рабочих местах локомотивных бригад и на территории застройки (в том числе жилой), близко расположенной к железнодорожному полотну. Кроме того, по формулам скоростей колебаний рельса определяются спектры виброскорости:

L = 201g— 5-10 8

И эти данные могут быть использованы при оценке воздействия вибраций на строения вблизи железнодорожного полотна.

Как видно из полученных зависимостей, снижения виброакустических характеристик рельса можно добиться за счёт увеличения диссипативных характеристик балластного слоя или самого рельса.