Моделирование видеоинформационного тракта оптико-электронных систем дистанционного зондирования земли: решения, проблемы и задачи

Видеоинформационный тракт оптико-электронных систем ДЗЗ – технически и математически сложная система преобразования визуальной информации. Для типовых оптико-электронных систем регистрации процесс преобразования информации может быть подразделён на несколько этапов, каждый из которых соответствует отдельным элементам тракта и описывается соответствующей математической моделью [1 – 11]. Результатом процесса моделирования является согласованная пара изображений: до (входное) и после (выходное) прохождения тракта. При этом основная ценность моделирования заключается не просто в получении прототипа «выходного» цифрового изображения, а в возможности оценить потребительские характеристики тракта, не прибегая к дорогостоящим или труднореализуемым натурным экспериментам [10, 11]. Информация о качестве цифровых изображений, получаемых в различных условиях съёмки, при разных параметрах аппаратуры, вариантах используемого оборудования и т.д., открывает возможность оптимизации как аппаратнотехнического наполнения оптико-электронной системы в частности, так и лётно-технических характеристик космического аппарата в целом [12].

В настоящей работе рассмотрены основные этапы преобразования визуальной информации в ви-деоинформационном тракте оптико-электронных систем ДЗЗ. В частности:

• -    преобразования в атмосфере, учитывающие поглощение и рассеяние оптического сигнала, турбулентность, облачность;

• -    преобразование в оптической системе, учитывающее дифракцию и дефокусировку объектива;

• -    преобразования в видеодатчике – приборе с зарядовой связью (ПЗС-линейке, ПЗС-матрице или ПЗС-матрице с временной задержкой и накоплением – ПЗС ВЗН);

• - аналогово-цифровое преобразование (АЦП) сигнала.

Для каждого из этапов преобразования представлены математические модели, методы и алгоритмы, лежащие в основе моделирования процесса оптического ДЗЗ. Проводится сравнение натурных и моделируемых изображений с целью выявления формальных (численных) и неформальных (визуальных) несоответствий между ними. На основании результатов сравнения определяются перспективные постановки и направления исследовательских работ.

Искажения атмосферы: облачность

Математически корректное описание динамических процессов формирования облачности в атмосфере – сама по себе чрезвычайно сложная математическая и вычислительная задача. Достаточно заметить, что в современной международной классификации облака делятся по внешнему виду на десять основных форм (родов). При этом в основных родах различают значительное число видов, разновидностей и дополнительных особенностей. Десять основных родов облаков приводятся ниже, включая их латинские названия и сокращения [13]:

– перистые – Cirrus (Ci),

– перисто-кучевые – Cirrocumulus (Cc),

– перисто-слоистые – Cirrostratus (Cs),

– высококучевые – Altocumulus (Ac),

– высокослоистые – Altostratus (As),

– слоисто-дождевые – Nimbostratus (Ns),

– слоисто-кучевые – Stratocumulus (Sc),

– слоистые – Stratus (St),

– кучевые – Cumulus (Cu),

– кучево-дождевые – Cumulonumbus (Cb).

На практике (в приложениях компьютерной графики) при моделировании облачности обычно используют гораздо более грубые модели следующих основных типов [14–24]:

– модели частиц;

– метасферы (metaballs);

– воксельная модель;

– фракталы;

– шумовые функции (случайные поля);

– текстурированные сплошные тела.

Указанные модели могут комбинироваться для достижения хороших результатов. Следует также отметить, что представленные модели являются не математическими, а имитационными в силу использованных в них многочисленных упрощений.

В своей работе мы использовали случайные поля как базис для построения некоторых моделей облачности. Для формирования непрерывного «облачного покрытия» был выбран шум Перлина (Perlin Noise) [24], идея синтеза которого заключается в комбинации шумовой и интерполяционной составляющих. Методы синтеза шума обладают такими преимуществами, как простота реализации и достаточно высокая степень реалистичности. Примеры синтеза Перлин-шума представлены на рис. 1 и 2.

Рис. 2. Пример реализации Перлин-шума

Поле, заполненное шумом Перлина, можно непосредственно использовать для визуализации слоёв непрерывной облачности : слоистых, слоистодождевых, перисто-слоистых типов облаков.

Для моделирования слоёв разрывной облачности мы использовали группы эллипсов, заполненных текстурой, сгенерированной методом Перлин-шума. Процесс моделирования в этом случае состоит из следующих этапов:

– выбор позиций фрагментов облачности на изображении;

– формирование группы эллипсов, представляющих фрагмент облачности в каждой позиции;

– заполнение эллипсов текстурой Перлин-шума.

Пример результата синтеза разрывной облачности, состоящего из трёх «фрагментов-эллипсов», представлен на рис. 3.

Рис. 3. Результат заполнения эллипсоидов Перлин-текстурой

Результатом моделирования облаков является набор изображений фрагментов облачности, для ка- ждого из которых заданы значения высоты расположения над поверхностью Земли и положение на спутниковом изображении, для которого моделируется облачность.

Заключительным этапом визуализации облаков на спутниковом изображении является отрисовка каждого фрагмента облачности и соответствующей ему тени на входном изображении. Для моделиро- вания тени существенными параметрами являются высота облака, положение солнца и положение точки наблюдения. В этом случае итоговое изображение (для одного отдельного облака) представляется в следующем виде:

x ⁽ t l , t 2 ) = Id ⁽ t l , t 2 ) ' I max +

⁺ x о ( t i , t 2 ) • I sh ( t i , t 2 ) - ( l ^- I_d ( t i , t 2 ) ) ,

где x0 (t1,12) - исходное изображение (входное для моделирования); Imax – максимальное значение яркости для моделируемого изображения; Icl – изображение облака (полутоновое, значение «0» интерпретируется как полностью прозрачный, со значением «1» – как полностью непрозрачный); Ish – изображение тени облака, определяемое по формуле:

I sh ⁽ t l , t 2 ) = ^{1 -} Id ⁽ t l — ^Д 1 , t 2 — ^Д 2 ) •

Здесь Д_р Д ₂ - сдвиг изображения тени относительно изображения облака (в метрах), определяемый соотношениями:

Д ₁ = H ( tan a s cos в _s - tan а_у cos Р_у ) ,

Д 2 = H (tan as sin вs - tan ay sin Py), где H - высота облака в метрах; a s ив s — положение (угловое) Солнца; ay и ру - положение (угловое) точки наблюдения/съёмки.

При визуализации нескольких фрагментов облачности, расположенных на различных высотах относительно поверхности земли, необходимо учитывать, что одни фрагменты могут «затенять» другие. В этом случае необходимо упорядочить фрагменты по высоте и накладывать их на моделируемое изображение от фрагментов с меньшей высотой к фрагментам с боль- шей высотой по описанному выше алгоритму. В этом случае выражение (1) используется столько раз, сколько облаков отрисовывается на изображении.

Пример изображения с помещённой облачностью и тенями представлен в конце работы, на рис. 6.

Искажения атмосферы: поглощение и турбулентность

По характеру искажений оптического сигнала атмосферные помехи разделяются на несколько групп [1 – 11].

Молекулярное поглощение излучения атмосферными газами приводит к энергетическим потерям в сигнале. Помехи от посторонних источников (рассеянное и отражённое солнечное излучение, собственное свечение атмосферы и земной поверхности и т. д.) проявляются в добавлении к сигналу независимой фоновой составляющей. Аэрозольное и молекулярное рассеяние отбирает у оптического сигнала часть энергии и передает её «рассеянной» сигнальной компоненте с низкочастотным пространственным спектром. Причём для высокоразрешающих систем дистанционного зондирования, наблюдающих детали поверхности с характерными размерами порядка единиц и десятков метров, рассеянную компоненту сигнала можно также отнести к фону. Таким образом, в рамках линейного приближения процессов переноса излучения, достаточного для большинства практических ситуаций, данная группа атмосферных искажений описывается простой математической моделью:

У(ti,t2) = aJJh(Ti,t2)x(, -Ti,12 —T2)d^idT2 + b, (2) D где x (t1, t2) – входной сигнал, поле истинной яркости земной поверхности; y (t1, t2) – выходной сигнал, поле яркости, наблюдаемое через атмосферу; a и b – параметры искажений: соответственно, коэффициент прозрачности атмосферы и яркость фона (0 < a < 1, b > 0); h (t1, t2 ) - функция размытия точки (ФРТ), обусловленная турбулентностью атмосферы. Из данных, приведённых в [6– 8, 25], следует, что эта ФРТ допускает довольно точную гауссовскую аппроксимацию:

h (^T i , ^T 2 ) = T^rexp 2 п r

2     2 Л

T i +Т г 1

2 r ² J ’

где r – параметр, служащий оценкой радиуса пятна «размытия» двумерного сигнала. При наблюдении земной поверхности из космоса в направлении, близком к надиру, в зависимости от состояния атмосферы значения r меняются от 1,7 до 10 см [25], т.е. оказываются меньше, чем пространственное разрешение большинства современных систем ДЗЗ.

При короткой экспозиции линейная модель искажений вида (2) также применима, но лишь для каждой локальной области двумерного сигнала: из-за пространственно-временных флуктуаций показателя преломления в турбулентных воздушных потоках ФРТ искажающей системы здесь оказывается случайной [9, 10]. Реализации этой случайной ФРТ име- ют вид узких положительных импульсов, лежащих в пределах пятна размытия сигнала при длительной экспозиции [9, 10]. Поэтому для большинства современных систем ДЗЗ искажениями, возникающими при короткой экспозиции в результате турбулентности атмосферы, можно пренебречь.

Искажения оптической части тракта

С помощью оптической системы поле яркости земной поверхности переводится в его изображение в фокальной плоскости объектива. Для оптики высокоразрешающих систем дистанционного зондирования, описываемой в параксиальном приближении, данный переход сопровождается масштабированием оптического сигнала, а также его пространственночастотными искажениями, моделируемыми двумерной ЛПП-системой [7, 8, 10, 12, 25]. Учитывая, что масштабирование не меняет «состав» регистрируемой видеодатчиком информации, преобразование сигнала y ( t 1 , t 2 ), поступающего на вход оптической системы после прохождения им атмосферы, может быть представлено в следующем виде:

^f ( ^t 1^, t 2 ) = JJ h op, (^T 1 , ^T 2 ) У ( t i ^-T 1 , t 2 — ^T 2 ) d ^T 1 d ^T 2 -

D

Здесь f ( t 1 , t 2 ) – поле яркости (сигнал) после оптической системы, поступающее на видеодатчик. Как известно, другое, во многих случаях более удобное описание ЛПП-системы даёт её амплитудно-частотная характеристика (АЧХ, в оптике – функция пространственной модуляции), определяемая как преобразование Фурье импульсной характеристики [10, 25]:

Hop, ( Q i , ^ 2 ) =

+to

= J J hop, ( ^T i , ^T 2 ) exp ( ^- i ( ^Q i ^T i ^{+ Q} 2 ^T 2 ) ) ^{d T} i d ^T 2

-to и устанавливающая простую связь между спектрами

Фурье входного Y ( Q i , Q 2 ) и выходного F ( Q i , Q 2 ) сигналов:

F(Qi,Q2) = Hop, (Qi,Q2)Y(Qi,Q2) -

В рамках таких представлений хорошо разрабо- таны математические модели конкретных типов оптических систем. Так, для идеального (безаберраци-онного) объектива с круглым зрачком при узкополосном (монохромном, но некогерентном) излучении [7, 10, 12]:

h op, ( ^T i , ^T 2 ) =

4 J i ( 0,5 Q 0 7 T 2 +t 2 )

^Q 0 V ^T 2 ^{+ t} 2

H ,(Q,, Q,) = opt 1 ,    2

П

(

arccos

У q 2 +Q 2 ¹

k

Q 0

J

У^Q i + ^Q 2 Г ^Q 2 + ^q 2 --i--:------

Q 0 V     Q 0

0, вне,

, при Q 2 +Q 2 0 ,

где J 1 ( . ) - функция Бесселя первого рода первого порядка, Q 0 - частота среза оптической системы:

Q = 2nd0  H X ’

где d – диаметр зрачка, H – расстояние наблюдения, X - длина волны светового излучения. Во многих реальных оптических системах высокого качества суммарное влияние остаточных аберраций при немонохромном излучении приближает импульсную характеристику к гауссоиде и, соответственно, частотную характеристику – к функции подобного же вида:

Hopt (Q,, Q2 ) = exp[-0,5r2 (Q, +Q2)], где r – экспериментально определяемый параметр.

Дефокусировка объектива с круглым зрачком моделируется ЛПП-системой с характеристиками [7, 10, 12, 25]:

h def (^T , , ^T 2 ) = ”

2 n r ² ’

2.2.2 при T, + T, <  r ,

0, вне,

H def ( Q , , Q 2 ) =

2 J, (r^Qf +Q2) r 4 q2 +q2

где r – радиус пятна размытия, который в единицах длины, приведённых к объектной плоскости (земной поверхности), задаётся выражением:

Ap dH

r =----- 2p2

где p - фокусное расстояние объектива, Ap - отклонение фокальной плоскости от плоскости изображения, d и H – то же, что и в формуле (3).

Искажения видеодатчика

ПЗС ВЗН датчик представляет собой матрицу M x M ₂ прямоугольных фоточувствительных электродов размером L , х L ₂ каждый, расположенных на плоскости с шагами S ₁ и S ₂ по вертикали и горизонтали соответственно. Электрод накапливает электрический заряд, пропорциональный интенсивности падающего излучения, площади электрода и времени накопления.

При работе датчика в K-тактном режиме ВЗН электроды объединяются по вертикали в группы по K штук и образуют единые ячейки, накапливающие «зарядовые пакеты». Через интервалы времени 0 происходит сдвиг каждой ячейки (зарядового пакета) на один электрод вниз по плоскости датчика. Поскольку обычно K << M , в рамках идеализированной модели датчика пренебрежём накоплением заряда в первых (K -,) тактах движения ячейки, когда она имеет неполный вертикальный размер, т.е. будем считать, что ячейка из K электродов последовательно занимает возможные (M - K +,) поло- жений. Изображение (поле интенсивности излучения) в плоскости датчика смещается с постоянной скоростью V1 по вертикали («догоняя» зарядовые пакеты) и V2 по горизонтали.

Считаем, что строка зарядовых пакетов после достижения нижнего положения на матрице электродов мгновенно передаётся на выход датчика (эта передача осуществляется с периодичностью K 0 ). Выведенная строка зарядовых пакетов соответствует строке отсчётов формируемого дискретного изображения.

Для такой модели датчика процесс формирования дискретного изображения описывается двухшаговой схемой [10]. На первом шаге происходит сглаживание непрерывного сигнала двумерной ЛПП-системой, моделирующей реально действующую на сигнал (эквивалентную, виртуальную) апертуру датчика. На втором шаге производится пространственная дискретизация сигнала по координатам. Величины шагов дискретизации непосредственно задаются параметрами датчика.

Виртуальная апертура датчика

АЧХ виртуальной апертуры идеализированного датчика имеет вид кратного произведения, в котором каждый из пяти сомножителей допускает определённую физическую интерпретацию [10]:

HCCD (Q,, Q2 ) = H0 (Q,, Q2) H, (Q,, Q2 ) х хH2 (Q,,Q2)H3 (Q,,Q2)H4 (Q,,Q2), где

. . Q, L . Q₂ L 4sin ^{1 1} sin ^{2 2}

H 0 ( Q , , Q 2 ) =

L _, L ₂ Q _, Q ₂

– АЧХ системы, усредняющей двумерный сигнал по площади электрода;

H , ( Q , , Q 2 ) =

sin PK K sin P

– АЧХ системы, описывающей формирование накапливающей ячейки из K электродов;

H 2 ( Q , , Q 2 ) = si QQ

– АЧХ «смаза» сигнала из-за различия непрерывного движения изображения и скачкообразного движения ячейки;

sin [(Q - P)(M - K + .

3 ( ,, 2)    (M -K +,)sin(Q-P)

– АЧХ «смаза» за счёт накопления зарядового пакета в ( M – K + 1) различных положениях ячейки при рассогласовании средней скорости её движения со скоростью изображения;

H4 (Q,, Q2 ) = expjz [Q (M + K-,)- P (M -,)]}

– чисто фазовая частотная характеристика, отражающая сдвиг выходного сигнала относительно входного. В приведённых выше формулах для краткости введены обозначения:

P = ^А Q = (QV +Q2 V2)®

2 ’ Q 2        .

В результате АЧХ сигнала z ( t 1 , 1 ₂ ) , искажённого

ЛЛП-системой видеодатчика, имеет вид:

Z (Q„ Q2 ) = H   (Q„ Q2)F (Q„ Q2).

Дискретизация сигнала по координатам

Пространственная дискретизация сигнала по координатам описывается простым соотношением:

z (i1, i 2) = z (i1 S1 + Л1, i2 S2 + Л2), i1, = 0, N, -1, i2 = 0, N2 -1.

Здесь Л 1 , Л ₂ - позиция «начала координат» для цифрового изображения в физической плоскости оптического сигнала; N ₁ – вертикальный размер цифрового изображения («высота» в отсчётах), характеризующий при моделировании «длительность» процесса съёмки; N ₂ – горизонтальный размер цифрового изображения («ширина» в отсчётах), который для большинства систем ДЗЗ удовлетворяет условию: N ₂ = M ₂.

– получение изображения-проекции x 0 ( t 1 , t 2 ) (промежуточный результат), учитывающего геометрию съёмки, рельеф и положение Солнца;

– моделирование съёмки с учётом характеристик видеоинформационного тракта (решение представлено в предшествующих разделах).

Заметим, что, учитывая «сканирующий» характер работы регистрирующего устройства (ПЗС ВЗН), задача построения изображения-проекции x 0 ( t 1 , t 2 ) может быть рассмотрена для одномерного случая, как представлено на рис. 4, где

– H – высота съёмки;

– центр регистрируемого изображения (толстая чёрная линия на рис. 4) расположен на расстоянии S от точки положения КА на земной поверх-

ности;

– W 1 – плоскость задания функции x ort ( t 1 , t 2 );

– W 2 – плоскость проекции – область задания функции x 0 ( t 1 , t 2 );

– L – дальность съёмки;

— ^a m _in, ^a max — предельные углы съёмки.

Математическая модель АЦП

Аналого-цифровое преобразование электрического сигнала, формируемого видеодатчиком, заключается в квантовании его амплитуды, т.е. в замене каждого значения отсчёта сигнала z (…) на один из «квантованных уровней» j . В наиболее широко распространённом случае равномерного квантования имеем [10, 25]:

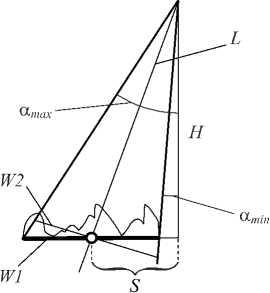
Рис. 4. Моделирование с учётом рельефа

С учётом сделанных обозначений, алгоритм синтеза изображения-проекции x 0 ( t 1 , t 2 ) на основании функции яркости x ort ( t 1 , t 2 ), рельефа r ( t 1 , t 2 ) и данных о геометрии базируется на простейших геометрических соотношениях. В частности, для каждой координаты t 2 выходного изображения x 0 ( t 1 , t 2 ) определяет угол визирования а ( 1 ₂) и затем соответствующее значение яркости x_ort ( t j , t _{а ( 1} 2 ) ). Учёт положения Солнца и позиции съёмки производится здесь же, на основании известных соотношений закона Ламберта [1, 2].

0,

z <  z min ;

jz = 1

z - z^

min

z max

^^^^^^в

z min

,   z min — z <  z max ^;

J - 1,

min .

Здесь J – число уровней квантования сигнала, [.] – знак выделения целой части числа, z min , z max – установленные границы шкалы сигнала.

Специфика моделирования с учётом рельефа Земли и геометрии съёмки

Пусть функция r ( t 1 , t 2 ) задаёт поверхность (рельеф Земли), характеризуя высоту поверхности в соответствующих координатах, а функция x ort ( t 1 , t 2 ) характеризует яркость (цвет) этой поверхности в тех же координатах.

Задача моделирования состоит в получении цифрового изображения z ( i 1 , i 2 ) (или его квантованного аналога j z ( i 1 , i 2 )), являющегося результатом съёмки заданной поверхности (Земли) с учётом известных позиций космического аппарата (КА) и параметров видеоинформационного тракта (в том числе положения Солнца). Данная задача, очевидно, разбивается на две независимые подзадачи:

Программный комплекс моделирования процессов ДЗЗ

Для исследования теоретических положений, методов и алгоритмов моделирования был разработан программный комплекс моделирования процесса ДЗЗ. Основными функциями программного комплекса являются:

• –    создание, изменение и сохранение модели ви-деоинформационного тракта;

• –    формирование покрытия территории геопривя-занными снимками (изображениями-прототипами);

– формирование покрытия территории геопривя-занными изображениями рельефов;

– моделирование процесса съёмки для отдельных изображений-прототипов покрытия, то есть получения по конкретному входному изображению соответствующего выходного изображения ДДЗ;

– моделирование процесса съёмки для заданной территории съёмки (с учётом рельефа);

– отображения статуса процесса моделирования;

– отображения служебных сообщений в процессе моделирования;

– интерактивное управление процессом моделирования.

Примеры некоторых экранных форм моделирующего программного комплекса приведены на рис. 5 а-в . Пример результата моделирования приведён на рис. 6.

Сравнение моделируемых и натурных изображений

Cравнение моделируемых и натурных изображений и определение собственно качества моделирования могут быть выполнены несколькими способами.

С одной стороны, формальным – сопоставляя основные числовые характеристики натурного изображения-прототипа и изображения, полученного после моделирования. В качестве формальных характеристик, численно определяющих качество цифровых изображений, могут выступать [26–29]:

– уровень шума на изображении;

– АЧХ системы искажения, полученная «слепым» методом идентификации.

К формальным способам проверки также можно отнести методы анализа подлинности цифровых изображений ДЗЗ , не защищённых цифровыми водяными знаками [30]. Целью этих методов является определение степени уверенности в том, что конкретное изображение ДЗЗ не является контрафактным . Это подразумевает, в частности, что анализируемое изображение ДЗЗ [31 – 33]:

– не было модифицировано до его поступления пользователю. Это подразумевает, в частности, проверку того, что изображение не содержит дубликатов (своего изображения или другого);

– не является полностью или частично синтезированным (компилированным);

– не взято полностью или частично с другого изображения;

– не было подвергнуто изменениям, приводящим к потере информации (JPEG-кодирование, ресэмплинг) и т.д.

В ИСОИ РАН были предложены подходы, методы, численные алгоритмы и информационные технологии анализа подлинности цифровых изображений ДЗЗ [32, 33]. Они решают ряд задач, классифицируемых на следующие группы:

– обнаружение дубликатов на изображении,

– выявление несоответствий в свойствах изображения,

– поиск изображений в БД,

а)

б)

в)

Рис. 5. Экранные формы моделирующего программного комплекса: размещение изображений-прототипов и рельефных данных на территории моделируемой съёмки (а);

предварительная 3D визуализация регистрируемых данных ДЗЗ (б); состав модели процесса ДЗЗ (в)

– проверка пролёта КА,

– проверка снимка на соответствие условиям съёмки (требует интерактивного участия человека),

– наличие признаков JPEG – сжатия изображения с потерями.

В целом, оригинальные наукоёмкие решения ИСОИ РАН позволяют обеспечить комплексную предмето-ориентированную безопасность данных космического ДЗЗ.

Наконец, качество моделирования может быть определено неформальным (визуальным) способом.

В данном случае эксперт (человек) определяет, является ли изображение действительно похожим на изображение дистанционного зондирования, полученное с конкретного КА, или нет.

Рис. 6. Пример изображения, полученного моделированием процесса ДЗЗ с наложением облачности

Ниже приведены результаты сравнений модельных и натурных изображений на предмет качественного соответствия указанным выше способам и проверяемым в них гипотезам (тестам).

Формальный анализ числовых характеристик

Для проведения анализа числовых характеристик было необходимо наличие двух множеств изображений ДЗЗ, первое из которых E _o является натурной съёмкой с конкретного КА, а второе, обозначаемое Е 1 , - результатом моделирования такой съёмки с параметрами аналогичного КА. В качестве натурных снимков выступали 25 моноспектральных снимков, полученных в спектральном диапазоне 0,61 – 0,68 мкм с разрешением 10 метров с французского КА Spot-4. В качестве снимков-источников для моделирования выступали снимки Индийского КА Cartosat (IRS-P5) в количестве N = 31 штук, получаемые с разрешением 2,5 метра в спектральном диапазоне 0,50–0,85 мкм. Относительно небольшое число используемых при моделировании изображений было вызвано достаточно большими объёмами обрабатываемых данных (размер снимка IRS-P5 составляет 12000×12000 отсчётов) и, как следствие, большим требуемым временем собственно моделирования (обработка снимка занимает от получаса до часа). В то же время выбранное число представляется достаточным для проводимого анализа.

Поскольку полные данные о съёмочной аппаратуре Spot-4 отсутствовали (доступные данные могут быть найдены на сайте ИТЦ «СканЭкс» и промо-сайте производителя продукта fr/spot4_gb/, по натурным моноспектральным снимкам с помощью оригинального метода [27] производилась идентификация неизвестных параметров оптико-электронного тракта SPOT-4 - АЧХ искажающей системы H (Q1, Q2) и среднеквадратическое отклонение (СКО) шума 5 .

Полученные оцененные параметры использовались для проведения моделирования и получения N «псевдо-SPOT» снимков на основе снимков IRS-P5.

N - 1):

I м

Для каждого из смоделированных изображений были рассчитаны характеристики искажающего тракта: оценка среднеквадратического отклонения шума 5 j и оценки АЧХ системы искажений ОЭТ H j ( Q 1 , Q 2 ) ( j = 0, N - 1). Методики определения этих характеристик представлены в работах [10, 26-29]. Степень «похожести» конкретного изображения с характеристиками 5 j и H j ( Q 1 , Q 2 ) на продукт КА Spot-4 определялась как относительное отклонение характеристики от соответствующего референтного значения, соответственно, 5 и H ( Q 1 , Q 2 )

(j = o

'        5

+да j f ( H j ( Q o , Q 1 ) - H ( Q o , Q i ) ) 2 d Q o d Q i

A H, = -------------------------------.

+да j j ( H ( Q o , Q 1 ) ) 2 d Q o d Q i -да

В табл. 1 –3 приведены распределения значений указанных отклонений.

Таблица 1. Относительное отклонение для шума (референтное значение 5 =0,8)

Интервал для A5	Частота отклонения
[0; 0,05]	0,129
(0,05; 0,1]	0,065
(0,1; 0,15]	0,032
(0,15; 0,2]	0,194
(0,2; 0,3]	0,194
(0,3; 0,4]	0,129
(0,4; 0,5]	0,097
(0,5; 0,6]	0,129
(0,6; 1]	0,032

Таблица 2. СКО шума (референтное значение 5 =0,8)

Интервал для 5 j	Частота попадания в интервал
[o; 5 ]	1
( 5 ; +да )	0

Таблица 3. Относительные отклонения для АЧХ

Интервал для A H	Частота отклонения
[0; 0,01]	0,387
(0,01; 0,02]	0,258
(0,02; 0,03]	0,226
(0,03; 0,04]	0,097
(0,04; 0,1]	0,032
(0,1; 1]	0

Как видно из табл. 3, отклонение по АЧХ на всём множестве смоделированных изображений не превышает 4%, причём практически для 97% изображений отклонение не превышает 3%. Это позволяет ут- верждать о практическом отсутствии отличий в АЧХ для смоделированных изображениях по сравнению с изображениями SPOT-4 и считать формальный тест на соответствие по АЧХ пройденным.

Отклонения величины шума от референтного значения δ = 0,8, как видно из табл. 1, достаточно существенные. В то же время дополнительный анализ, представленный в табл. 2, показывает, что абсолютно все смоделированные изображения искажены шумом с заведомо меньшим значением дисперсии. Такая ситуация (значительное систематическое смещение среднего) может быть объяснена недостаточной точностью выбранной методики оценки. При этом, очевидно, оказывается возможной апостериорная коррекция шума до требуемого уровня путём добавления синтезированного «белого шума» к полученному изображению [25]. Поскольку такая коррекция позволяет получить шум требуемого уровня ( δ = 0,8) с любой наперёд заданной точностью (эксперимент здесь ввиду предопределённости результата не представлен), тест по уровню шума также можно считать пройденным .

Формальный анализ подлинности цифровых изображений

Анализ подлинности, как было отмечено ранее, заключается в решении ряда задач, каждая из которых предназначена для выявления определённого «нарушения»: наличие дубликата, наличие признаков JPEG – сжатия, наличие в БД снимков аналога и т.п. Указанные «нарушения» возникают в тех случаях, когда изображения синтезируются (компилируются) из других изображений посредством специальных операций. Учитывая это, некоторые из «нарушений» не могут быть обнаружены на модельных изображениях по причине принципиального отсутствия в процессе моделирования соответствующих «нарушениям» операций. К таким нарушениям, в частности, относятся:

• –    наличие дубликата фрагмента на том же изображении, поскольку процесс моделирования не выполняет дублирование фрагментов;

• –    наличие несоответствий в свойствах изображения, поскольку параметры моделирования одинаковы для всех частей изображения;

• –    наличие признаков JPEG – сжатия изображения с потерями, поскольку моделирование не включает в себя процесс сжатия.

С другой стороны, есть «нарушение», которое может быть обнаружено вне зависимости от качества собственно моделирования – это несоответствие данным о пролёте КА. Поскольку данные о пролёте содержатся в метаданных продукта ДЗЗ, собственно содержание изображения ДЗЗ на результат прохождения теста никак не влияет.

Наконец, существуют «нарушения», которые заведомо будут обнаружены практически у всех проверяемых изображений. К таким нарушениям, в первую очередь, относится нахождение для смоделированного изображения в БД изображения-прототипа. По- скольку моделирование предполагает использование изображения-прототипа, проблема обнаружения такого «нарушения» фактически сводится к задаче ведения достаточно полной БД изображений ДЗЗ. К аналогичным «нарушениям» относится также и «нарушение», связанное с несоответствием условиям съёмки (угол съёмки и угол положения Солнца). При ненадлежащем выборе изображения-прототипа по изображению урбанизированных построек даже неподготовленный пользователь легко обнаружит подделку. Относительным недостатком последнего теста является необходимость участия в нём человека, что на данный момент делает этот тест достаточно трудоёмким, не позволяя его полностью автоматизировать.

Представленный качественный анализ тестов подлинности сведён в таблицу 4.

Таблица 4. Тесты формального анализа подлинности цифровых изображений ДЗЗ

Наименование теста	Результат прохождения
наличие дубликатов	пройден
выявление несоответствий в свойствах изображения	пройден
поиск изображений в БД	не пройден
проверка пролёта КА	опционально
проверка снимка на соответствие условиям съёмки	не пройден
наличие признаков JPEG – сжатия изображения с потерями	пройден

Экспертный анализ изображений

В качестве данных для сравнения использовались множества натурных Ξ ₀ и модельных Ξ ₁ изображений. Заметим, что в состав множества Ξ ₁ модельных изображений входило семь изображений с моделированной облачностью. Множества изображений Ξ ₀ и Ξ ₁ объединялись для получения материалов, подаваемых для анализа экспертами. В качестве экспертов выступали три специалиста по приёму данных ДЗЗ Центра приёма и обработки космической информации ФГБОУ ВПО «Самарский государственный аэрокосмический университет имени академика С.П. Королёва (национальный исследовательский университет)». Экспертам относительно каждого изображения на основании его визуального анализа необходимо было указать, является ли оно фрагментом натурного снимка Spot-4 или получено путём моделирования. Распределение числа натурных и модельных изображений экспертам не сообщалось. Экспертам были предоставлены примеры натурных изображений Spot-4 (по другим территориям съёмки), а также информация о том, что для моделирования использовались снимки IRS-P5. Процесс анализа всех изображений занимал у каждого эксперта от двух до четырёх часов. Результаты проведённого эксперимента представлены ниже, в табл. 5.

На основании приведённых результатов можно сделать следующие предварительные выводы.

Таблица 5. Результаты экспертного анализа изображений

Наименование	Частота
	эксперт 1	эксперт 2	эксперт 3
Верное определение снимков SPOT	0,87	0,67	0,89
Верное определение снимков «псевдо-SPOT» (облачность НЕ моделируется)	0,83	0,96	0,08
Верное определение снимков «псевдо-SPOT» (облачность моделируется)	1,00	0,71	1,00

Во-первых, все эксперты достаточно уверенно определяли «Псевдо-SPOT» снимки, если на изображении моделировалась « облачность ». Во-вторых, для остального множества снимков результаты сильно разнились, что можно объяснить опытностью специалистов (третий эксперт практически не распознал «псевдо-SPOT» изображения). Ориентируясь на результаты первых двух экспертов, можно сделать вывод о способности квалифицированного и опытного эксперта различить SPOT и «псевдо-SPOT» изображения с достаточно высокой степенью достоверности. Анализ результатов, проведённый вместе с экспертами, выявил следующие причины:

• а)    в SPOT-изображениях реальные облака оказываются «засвеченными» (выходят за динамический диапазон), в то время как в изображениях IRS-P5 они регистрируются в полутонах (диапазона хватает);

• б)    в продуктах SPOT и IRS-P5 присутствуют существенные различия в отображении зелёных насаждений, в частности леса и его границ (для SPOT – тёмный, для IRS-P5 – светлый). Данный факт вызван значительным различием в спектральных диапазонах, в которых работают эти КА;

• в)    в силу конструктивных особенностей аппаратов, расположение камер IRS-P5 наклонное (фиксированный ненулевой угол тангажа и изменяемый угол крена), в то время как SPOT чаще всего производит съёмку в надир. Это добавляет в снимки IRS-P5 легко узнаваемые искажения перспективного характера.

Названные причины позволили экспертам достаточно уверенно отличать SPOT от «Псевдо-SPOT» изображений.

Непосредственные выводы по результатам экспериментов

Основные выводы по представленным результатам сравнения могут быть сформулированы следующим образом.

• I.    При адекватно подобранных параметрах моделирования полностью автоматический формальный анализ изображений ДЗЗ не позволяет определить , было ли изображение натурным или получено путём моделирования.

• II.    Формальный (и полностью автоматический) анализ позволяет гарантированно распознать смоделированное изображение по его изображению-прототипу (исходное псевдонепрерывное изображение), если таковое доступно системе анализа (изображение находится в БД изображений ДЗЗ).

• III.    Формальный анализ оказывается полезным при анализе снимков в ситуации, когда снимок проверяется на соответствие условиям съёмки, что требует участия человека .

• IV.    Неформальный (визуальный) анализ изображений ДЗЗ позволяет практически всегда отличить моделируемые изображения, если на них моделируется « облачность ».

• V.    Квалифицированные и опытные эксперты способны различить натурные и моделируемые изображения с достаточно высокой степенью достоверности.

Качественные выводы

Как следует из представленных выше непосредственных выводов по экспериментам, формальный анализ числовых характеристик искомого цифрового изображения не позволяет отличить натурное изображение от cмоделированного. В то же время, привлечение дополнительной информации – метаданных съёмки (ориентация камер, используемый спектральный диапазон, используемый динамический диапазон), базы данных изображений ДЗЗ, интеллектуальной информации об изображённых объектах урбанизированного (здания) или натурного (облака, лес) характера – позволяет относительно легко отличить смоделированное изображение от натурного. Этот факт приводит к следующему качественному выводу относительно процесса моделирования: современные модели, методы, алгоритмы и информационные технологии моделирования данных ДЗЗ обязаны привлекать всю доступную информацию (в том числе – высокоуровневую и интеллектуальную) о сцене съёмки и характеристиках процесса регистрации для получения результата, неотличимого от натурного изображения . Предварительный анализ проблемы позволяет выделить целый ряд факторов, которые оказывают влияние на результат моделирования и которые в обязательном порядке должны быть учтены при моделировании:

• –    метаданные, определяющие геометрию съёмки и параметры модели, специфику цифрового тракта;

• –    специфические параметры погоды (давление, направление ветра и др.), характеризующие вид отдельных облаков, плотность облачности, её ориентацию и ориентацию дождевых «шлейфов» на снимке и т.п.;

• – состав, взаимное расположение и характер / геометрию изображённых на снимке объектов (в особенности – урбанизированных объектов);

  – наличие «стыков» (геометрическое рассогласованных изображений в изображении-композите), возникающих при формировании изображения-прототипа съёмки. Для иллюстрации этого пункта на рис. 7 представлен пример покрытия, сформированного в программе Google

Earth. Очевидно, что даже неподготовленный человек легко обнаружит «шов» на изображении и, как следствие, определит изображение как «ненатурное»;

– динамику изменения объектов урбанизированного и натурного происхождений (строительство дороги, домов, вырубка или рекреация лесов и т.п.);

– специфику получения и характеристики псевдо-непрерывного «изображения-источника», ис- пользуемого для моделирования.

Представленные качественные выводы делают актуальными два блока проблем, связанных как с учётом при моделировании указанных факторов, так и с разработкой полностью автоматических методов их детектирования (например, алгоритмов нахождения «стыков» на изображениях, подобных приведённому на рис. 7).

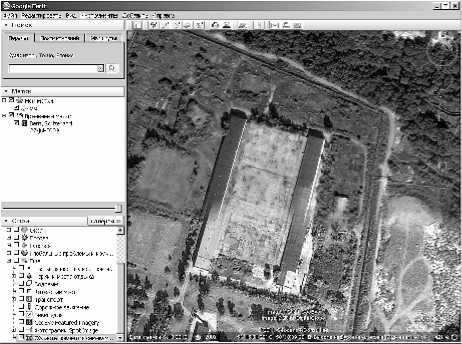
Рис. 7. Пример стыковки отдельных изображений в Google Earth

Заключение

Моделирование цифровых изображений ДЗЗ – математически и технически сложная задача. При этом существующие в настоящее время модели, методы, алгоритмы и программные средства позволяют получить результат, который формальными автоматическими вычислительными процедурами распознаётся как «ненатурное» изображение только в исключительных случаях (наличие изображений-прототипов в базе данных). В то же время визуальный неформальный анализ позволяет получить правильный ответ относительно смоделированного снимка существенно чаще.

Полученные в работе результаты и сформулированные выводы обуславливают необходимость создания новых и развития существующих моделей, методов и алгоритмов моделирования по ряду направлений. В том числе, наиболее перспективным представляется:

– развитие методов моделирования с целью учёта дополнительной информации о регистрируемой сцене (метаданных, векторных данных об изображённых урбанизированных и натурных объектах, специфики их развития и изменения и т.п.);

– создание новых методов моделирования облачности, позволяющих получать визуально не отличимые от натурных изображения;

– развитие методов синтеза «бесшовных покрытий» из цифровых снимков;

– определение возможности устранения и устранение «специфики» изображений-источников, используемых для моделирования.

В плане разработки методов и алгоритмов анализа изображений с целью определения их подлинности представляются перспективными следующие направления:

– разработка высокоскоростных методов поиска изображений ДЗЗ и их фрагментов в БД изображений;

– разработка методов и алгоритмов определения соответствия цифрового изображения указанному продукту КА (соответствие изображений объектов по спектральным характеристикам и т.п.);

– разработка методов полностью автоматического определения параметров съёмки (высоты Солнца и позиции КА) и/или их проверки по данным ДЗЗ (анализ теней, ракурсов съёмки и т.п.);

– разработка методов и алгоритмов обнаружения и анализа «облачности» на изображении;

– создание методов и алгоритмов обнаружения и анализа «швов» на цифровых снимках;

– создание инфотелекоммуникационной инфраструктуры данных ДЗЗ с поддержкой функций распределённого поиска (сервисов поиска) [34].

Работа выполнена при частичной финансовой поддержке:

– грантов РФФИ (проекты 11-07-12059-офи-м-2011, 11-07-12060-офи-м-2011, 11-07-12062-офи-м-2011);

– программы фундаментальных исследований Президиума РАН «Фундаментальные проблемы информатики и информационных технологий», проект 2.12;

– гранта Президента РФ № НШ-4128.2012.9.

Авторы также выражают благодарность специалистам Центра приёма и обработки космической информации ФГБОУ ВПО «Самарский государственный аэрокосмический университет имени академика С.П. Королёва (национальный исследовательский университет)» Копенкову В.Н. и Титовой О.А. за участие в эксперименте.