Моделирование влияния динамики углового движения колеса на вертикальные колебания транспортного средства

Введение. В настоящее время довольно остро стоит проблема удешевления железнодорожных и автотранспортных перевозок. Существенно сократить издержки в этой сфере позволит проектирование современных систем автоматического управления транспортными средствами, в контуре управления которыми нет человека. Для современных сложных динамических транспортных систем принципиальное значение приобретают вопросы построения моделей, опи-

–

—

Машиностроение и машиноведение

влияния динамики вертикальных колебаний центров масс транспортного средства на тяговые и скоростные характеристики процесса управления.

Задача синтеза модели, описывающей вертикальные колебания, не нова. Ее решению посвящено значительное количество работ — как о железнодорожной технике [6, 7], так и об автомобильной [8-11]. Отметим, что в этих моделях не учитывается взаимовлияние координат вращательного движения колеса и координат, описывающих вертикальное движение центра масс колеса и кузова транспортного средства. Вместе с тем, такое влияние подтверждено экспериментально [10, 11]. Это позволяет сделать вывод о необходимости математического описания данного явления. Итак, синтез качественной модели, отражающей указанную связь, является актуальной научной и практической задачей, чему и посвящен представленный материал.

Модель динамики вертикальных колебаний. При построении моделей, описывающих сложную динамику систем управления, часто возникает противоречие между требованием к точности модели и ее сложности. Однако для качественного анализа основных форм колебаний в транспортном средстве достаточно принять двухмассовую модель, которая в упрощенном виде представлена на рис. 1.

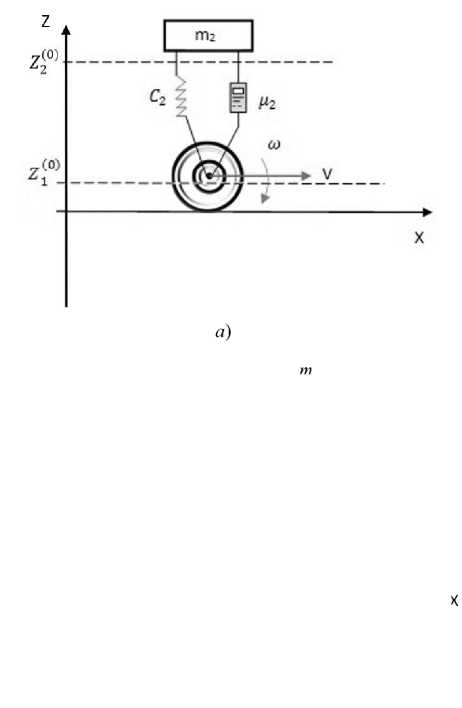
Рис. 1. Модель динамики транспортного средства: в координатах состояния (а ); упрощенная двухмассовая модель (б)

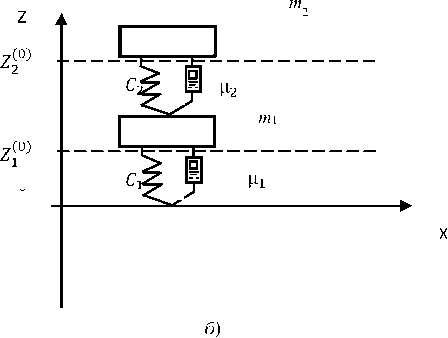
На рис. 1 m i , m 2 — массы колесной пары и кузова соответственно; c 1 , c 2 — характеристики жесткости колеса и подвески соответственно; р 1, Ц2 —коэффициенты, характеризующие диссипацию в колесе и в подвеске соответственно. Горизонтальной пунктирной линией отмечены уровни, соответствующие положению статического равновесия центра масс кузова и колеса. Начало отсчета поместим на этих уровнях, а ось 0 z будет направлена вверх. Если центр масс кузова или колеса находится выше положения статического равновесия, то их координаты z 1 , z 2 > 0, если ниже, то z 1 , z 2 < 0. С точки зрения анализа вертикальных колебаний транспортного средства, возникающих в нормальной плоскости, удобно представлять колесо в виде упруго-жесткой связи. Так, к примеру, делают при решении задач моделирования в автомобильной технике [8-11].

Значение деформации подвески с достаточной степенью точности можно определить как:

М, = 5   ₀         ,

2 стат.2      2      1 , mg гДе S^.2 =—--статическая осадка пружины подвески под действием силы тяжести. c 2

Для построения модели, отражающей динамику вертикальных колебаний центров масс колеса и кузова автомобиля, используем широко известный подход, предполагающий использование уравнения Лагранжа второго рода [4]. Однако при этом примем в расчет влияние времени существования контакта. Для этого с учетом направления осей z 1 , z 2 введем дополнительную функцию, отражающую эффект «всплывания колеса», который проявляется при увеличении скорости вращения. Подобный эффект достаточно хорошо изучен в динамке металлорежущих станков. Например, в [12, 13] этот эффект объясняется гидродинамической составляющей сил, возникающих в зоне контактирующих поверхностей. В рассматриваемом случае учитывается существование контакта не только в режиме относительного скольжения колеса, но и в режиме качения. Поэтому «всплывание колеса» можно объяснить тем, что контакт колеса и дороги формируется не мгновенно, а в течение некоторого времени. Под временем формирования контакта колеса и дороги мы понимаем время, которое будет потрачено на деформацию в нормальной плоскости колеса. Обозначим время формирования контакта, которое также является и временем существования контакта, величиной А t Не вдаваясь в глубокий анализ процессов, происходящих в зоне контакта при сближении поверхностей колеса и дороги, отметим, что существует некоторое эффективное значение А tk^. , при котором сцепление колеса и дороги достигает некоторого максимального значения и при котором деформация колеса в нормальной плоскости останавливается.

С учетом вышеизложенного и при условии, что А t <А tк, значение деформационных изменений колеса в нор

:

А l1   ^ стат.1   z1   f (Аt), где f (Аt) — некоторая неизвестная функция, учитывающая влияние времени существования контакта на величину

( m ₁ + m ₂) g ¹² —

деформационных изменений колеса в нормальной плоскости, а 5.1

ка) колеса под действием веса кузова и колеса. Если А t >А t к, ТО

А l1   ^стат.1

При А t < А t к будут справедливы два следующих предела:

lim f ( А t) ^ ^стат .1, lim f (Кt)0.

А t ->Д t_k

С достаточной степенью точности такое изменение f (^Д t ) можно описать при помощи следующей функции:

Подставим (4) в (1) получим:

f (А t )    ^ стат .1

_А t_k

1 -е ^4t

.

А t_k

Д l, = 8_,е^{А t} — 7

1     ^истат .1            1 .

Для дальнейшего анализа уравнения (5) выразим А t и А t к в координатах состояния. Для этого рассмотрим зависимость времени существования контакта от длины площадки контакта и скорости углового движения колеса.

Пусть R — радиус колеса; 6 — угол между двумя прямыми, соединяющими центр колеса с двумя противоположными краями площадки контакта; А l 1 — величина, характеризующая степень деформации колеса, под действием нормально приложенной нагрузки (5); L — формируемая длина площадки контакта.

С учетом принятых обозначений можно определить угловую величину сектора колеса, принимающего участие в контакте — 6. Для этого найдем L :

L 2А l 1(2 R -А l 1) ,                                              (6)

а затем, используя известные тригонометрические соотношения, определим значение 6:

. е_А l 1(2 R -А ^l 1⁾ sin ^{1           1}

со           R

Для железнодорожной техники угол 9/2 достаточно мал. С учетом этого, используя известную теорему о предельном значении бесконечно малых величин, будет справедливо:

Машиностроение и машиноведение

Э- ²■А l 1(2 R -А l ₁) . со

Время формирования площадки контакта можно связать с ее угловой характеристикой (8) и скоростью вращения колеса следующим образом:

, е t ,

—

—

t

L

— t

.

t                                            — t

V

.

l 1

f ( l ₁ )

f ( l 1)    K R l 1,

KR                                                                   f   l 1                                            l1

R = 0,5 KR 14):

2K  l t R1

R

.

t k Vk

Преобразуем выражение (5) к виду

k

1                     .1                     1 .

Как видно из (12), от скорости вращения колеса зависит степень его деформации под действием нормально приложенной нагрузки. Это позволяет говорить о взаимосвязанности динамики углового движения колеса (колесной пары в железнодорожной технике) и динамики вертикального колебательного движения в нормальной плоскости центров масс колеса и кузова.

z 1 , z 2

k

1                     .1                     1,

А — 5 о — z-, ~V" z,.

2                .2       2       1.

Уравнение Лагранжа, описывающее динамику взаимосвязанного движения центров масс кузова и колеса в нормальной плоскости, примет следующий вид:

d2z      dz             dz m 2       2 cz        1 cz,

² dt ^{2      2} dt ^{2 2     2} dt ^{2 1}

d2z            dz                        dz m1 dt21 ( 1     2) dt1 (c1 c2)z1 c2z2     2 dt2

g ( m m )(1 e ^k )    ^{1     .1} e ^{k d} .

1      2                        _k             dt

Система (14) описывает динамику вертикального движения центров масс кузова и колеса. Отметим, что, если угловое движение отсутствует, то последние два члена второго уравнения системы будут равны нулю, и система (14) преобразуется к линейному виду. – — —

Кроме того, с учетом связи через проскальзывание в данном случае принимается во внимание и поступательное движение.

Результаты численного моделирования. Проанализируем динамику вертикальных колебаний, описываемых системой (14). Для этого в качестве параметров уравнений, входящих в систему, подберем величины, соответствую- m 2 = 50000

c 2 = 1 10⁷ Н/м; ц2 = 40000 Н/(м/с); m 1 = 300 кг; c 1 = 1,6 10⁷ Н/м; ц1 = 4000 Н/(м/с). Тогда значение 5_{стат .1} = 0,0314 м; ^стат _.2 = 0,05 м; Kстаб. примем равным 0,99; го k = 40 рад/с (72 км/ч) при R = 0,5.

Для проведения эксперимента по оценке динамики транспортного средства в качестве возмущающего воздействия использовались изменения начальных условий по координате z 1. То есть моделировалась неровность дороги (рельса), при этом скорость вращения колеса совершала колебания относительно некоторого стационарного значения, что может соответствовать порывам встречного ветра. Результаты моделирования вертикальной реакции колеса представлены рис. 2, 3.

dz ₁ dt

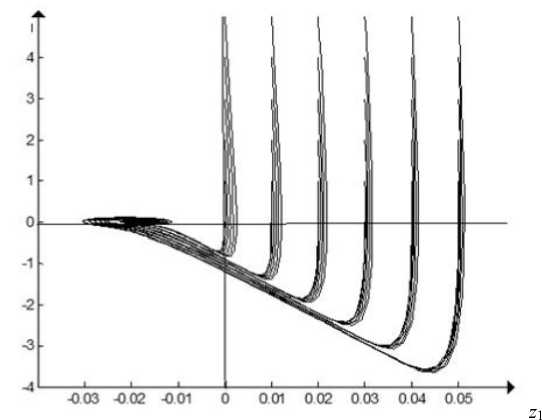
Рис. 2. Фазовый портрет колебательного движения центра масс колеса при V = 72 км/ч

Реакция на возникающие неровности, представленная фазовым портретом на рис. 2, носит колебательный характер. Взяты значения встречающихся неровностей, не превышающие степень статической деформации колеса ( ^стат _.1= 0,0314м). Однако, как видно из рис. 2, при увеличении скорости транспортного средства на неровной поверхности возможна потеря контакта колеса с дорогой. Из опыта эксплуатации транспортных систем известно, что на неровной дороге транспортное средство должно уменьшать свою скорость. В противном случае возможна потеря управляемости. Для проверки адекватности модели мы увеличили скорость. Результаты моделирования системы представлены на рис. 3.

dz ₁ dt

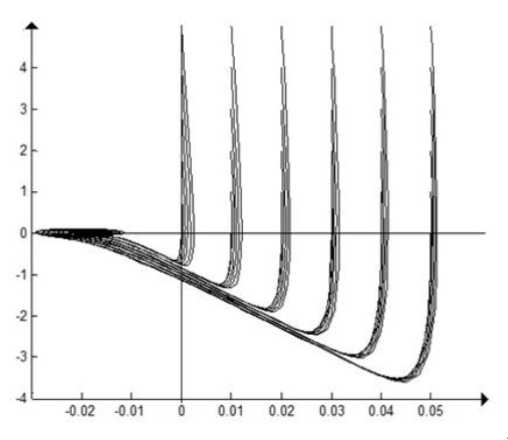
z 1

Рис. 3. Фазовый портрет колебательного движения центра масс колеса при V = 135 км/ч

Машиностроение и машиноведение

Как видно из рис. 3, с увеличением скорости движения транспортного средства растет вероятность потери управления (контакта колеса с дорогой) на неровной поверхности. Таким образом, адекватность принятой модели подтверждается.

Кузов транспортного средства тоже реагирует на возникающие неровности. Результатом такой реакции должны быть колебания центра масс кузова. Эффект «всплывания» колеса при увеличении скорости движения определяет сложный характер этих колебаний. С точки зрения проверки адекватности модели, правильно давать приращения ко- z1

z 2

ва от величины возникающих на пути неровностей. Результаты моделирования вертикальных колебаний кузова транспортного средства представлены на рис. 4.

dz ₂ dt

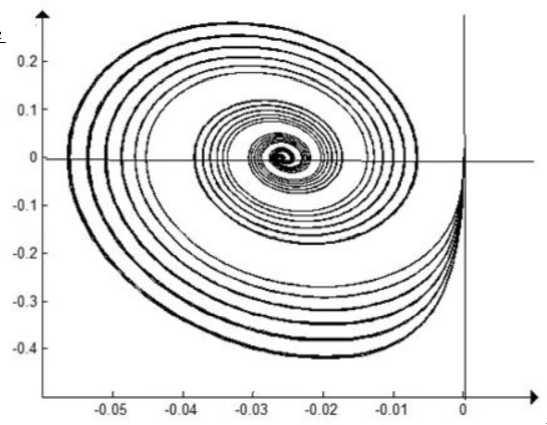
Рис. 4. Фазовый портрет колебаний кузова

z 2

Как видно из рис. 4, кузов транспортного средства совершает более сложное колебательное движение, чем колесо. Однако в отличие от динамики вертикальных колебаний центра масс колеса, центр масс кузова меньше реагирует на колебательные изменения скорости движения транспортного средства, то есть колебания затухают.

Заключение. Представленная в статье модель позволяет численно определять степень влияния скорости транспортного средства на динамику вертикальных колебаний центров масс кузова и колеса. Это позволит проектировать сложные системы управления движением транспорта. Результаты численного моделирования позволяют сделать вывод об адекватности принятой модели. Колебательный характер нарастания скорости транспортного средства обусловливает колебательный характер движения центра масс колеса вблизи равновесного состояния. При увеличении скорости движения увеличивается «всплывание» колеса и отмечается некоторый подъем кузова. При синтезе модели

—

2– не только весом, но и упругой силой, связанной с деформацией пружины подвески. Отметим, что рассматриваемый – в работе модель приводиться впервые.

В качестве дальнейшего развития предлагаемого подхода авторы рассматривают синтез связанной модели колебательного движения всего транспортного средства с учетом взаимодействия углового и поступательного движения колеса при проскальзывании.