Моделирование влияния допускаемых отклонения размеров деталей замкового соединения диска и лопатки ГТД на напряженное состояние
Автор: Овсеенко А.Б., Шукаев С.Н., Заховайко А.А.
Статья в выпуске: 2, 1994 года.
Бесплатный доступ
Приведены результаты теоретического исследования напряжений в двигательных единицах в зависимости от отклонения размеров.
Короткий адрес: https://sciup.org/146211730
IDR: 146211730 | УДК: 539.3
Текст научной статьи Моделирование влияния допускаемых отклонения размеров деталей замкового соединения диска и лопатки ГТД на напряженное состояние
Введение.
Соединения ”диск-лопатка” газотурбинных двигателей работают в сложных условиях термосилового нагружения. Как показывает опыт эксплуатации, разрушение таких соединений происходит по механизму малоцикловой усталости. В общей проблеме оценки долговечности соединений особое место занимает проблема повышения точности расчетов напряженно-деформированного состояния. Для этой цели нужно ставить и решать задачу в условиях, максимально приближенных к эксплуатационным, т.е. учитывать такие факторы: - влияние сил инерции; - температурные градиенты; - упругопластическое поведение материала-. - контактное взаимодействие между хвостовиком лопатки и пазом диска.
Для решения двумерных контактных краевых задач был разработан конечно-элементный программный комплекс ДКАРС, реализующий принцип раздельного рассмотрения тел и поочередного задания граничных условий cci],(2;лзз>. Пакет программ реализован для персональных ЭВМ типа ibm рс ат з№. Он снабжен мощными средствами визуализации полученных полей и сеток на экране монитора.
Расчеты замковых соединений в контактной постановке уже проводились ранее различными исследователями с 4), с so и др. Пользуясь тем, что в реализованном методе контактирующие тела рассматриваются раздельно и сетки для них строятся независимо друг от друга, была проведена серия расчетов для замкового соединения типа “ласточкин хвост", где геометрические размеры в области контактной зоны, брались с учетом предельных допускаемых отклонений.
Задача ставилась в предположении о плоском напряженном состоянии с учетом разнотолщинности контактирующих тел. Схема нагружения замкового соединения представлена на рисл.
Рисл . Расчетная схема замкового соединения.
Варьируемые размеры: размер по базовой поверхности ь и угол . Номинальный размер ь=15.4тт , номинальный угол р=бо°. Допускаемое отклонение размера ь: для лопатки дь =-о.о4 mm. для диска дь1=+о.оо4 mm. Допускаемое отклонение угла у. для лопатки др^+в"' , для диска др2—4°. Всего получилось is возможных комбинаций допусков.
Расчеты проводил 'съ по схеме полного факторного эксперимента 42//1б с четыре фактора на двух уровнях, всего ie опытов^ Для упрощения вычислений и интерпретации полученных результатов факторную модель постулировали в виде ортогональных полиномов Чебышева. В таблице i приведены уровни варьируемых факторов и формулы перехода от натуральных их значений к кодированным.
Таблица I.
|
Наимено вание элемента соеди нения |
Наименование фактора |
Натураль ное зна чение фактора |
Кодиро ванное значение фактора |
Формулы перехода от натуральных значении факторов к кодированным |
|
Лопатка |
Отклонение размера Ь, , нм |
о |
-1 |
х =-С1/0. 023СДЬ + +О.023 |
|
-0. 04 |
1 |
|||
|
Отклонение размера <р, Др^,минуты |
О |
-1 |
х =0.25еСД<р --4> 2 1 |
|
|
8 |
1 |
|||
|
Диск |
Отклонение размера Ь, ДЬ , мн 2 |
О |
-1 |
х =С1/0.O2DСДЬ - 3 2 -О. 023 |
|
О. 04 |
1 |
|||
|
Отклонение размера ^, Др^ , минуты |
О |
-1 |
х =—СО. 5} С Др +23 4 2 |
|
|
-4 |
1 |
Для численного решения поставленой задачи были построены конечноэлементные сетки для диска и хвостовика лопатки. Для диска сетка была построена лишь для сектора, содержащего один паз. На поверхностях выреза сектора задавались условия
Моделирование влияния доп'"' <о.е7лк оту ■■ ^ечай циклической симметрии, заключающейся в равенстзэ перемещений нэ этил поверхностях для точек, лежащих па одной радиусе. Сотка СОДЕРЖИТ 236 КВаДраТИЧНЫХ В-узЛОВЕХ ЭЖТОПТОВ И 747 УЗЛОВ. ДЛЯ лог.эткч рассматривалась сетка лишь хвостовика. Эна содержит тол элемента и поз узлов. При этом граничные условия по поверхности отсечения профильной части сеч зтф'бсжнав сила топа и изп^зюжй моиетгг от действия газода{ткос№й сил и сил иердию удовж - ворялись интегрально.
Условия нагружения таковы. Скорость вращения диска п-тоато об/мин Центробежная сила лопатки Стото.ез кь, центробежнол сила профильной части Cn=ie,e7 кн , j , .дхе, нзя сила хвостовика Сито, за кн , Изгибающий. момент жро лопат?® Етоэ.то нн-шт Б ому плоской постановки задачи оказались неучтенными изпюьйщий но пит в перпендикулярном направленин и крутящий момент на пере нтки. Задавалось равномерное пето температур тото’ как в так и в хвостовике лопатки.
Материал диска и топотки - титановый сплав ВТ-з-т. Его механические характеристики: модуль tea e-1.14e.-1 о3 МПа, коэффициент Пуассона мто„зз , т^едзл текучести о ,=87о МПа , предел пропорциональности что'70 Mite „ предел грочностп =эвв МПэ .
Первоначально был провэдея отдельтый расчет диска и хвостовика лопатки в неконтактосн лолтарозке под дойс’гвием только сил инерции. Для сектора диска получтмось решение, бжзкоо к аналитическому сот. Для хезостовикз лопатки при жестком закрэппании поверхности отсечения ирофяьькоя части интегральное усичие на этой поверхности получаюсь Сд-еуз? кн „ что на зх оттмчаутся от известного значения С . Таким образом, пг этим прэдавригэльным расчетам можно сказать, что сетки диска и кз.тг'ОБИка лопатки построены прсБИЛьчо л разнптолдивностъ учтена зерно.
Итак, было выполнено то расчетов в контактной постановке раз.етыых сочетаниях предельных отклонений выбраных размеров. Граничные условия для хвостовика задавались в перемещениях на поверхности отсечения профильной части лопатки, таким образом, чтобы на этой поверхности интегральное осевое усилие было равно т'-^ , поперечное усилие ото, изгибающий момент М=МД .
Результаты расчетов приведены в табл.г. в качестве функций отклика используются максимальная интенсивность напряжений в диска е^ тох >. максимальная интенсивность напряжений в лопатке
, максимальное контактное давление р .
Таблица 2.
|
N |
Лопатка |
Диск |
2 |
с” max’™8 |
Р , МПа тех |
||
|
b , mm |
Д«? ♦ mm 1 |
ДЬ , mrn 2 |
|||||
|
1 |
0 |
0 |
О |
0 |
580 |
546 |
742 |
|
2 |
о |
0 |
-4" |
573 . |
502 |
682 |
|
|
3 |
0 |
о |
0 04 |
0 |
607 |
446 |
523 |
|
4 |
0 |
о |
О. 04 |
-4 “ |
608 |
453 |
531 |
|
5 |
о |
8° |
0 |
О |
877 |
466 |
619 |
|
6 |
0 |
8° |
0 |
-4° |
575 |
435 |
612 |
|
0 |
8° |
О. 04 |
О |
613 |
457 |
534 |
|
|
8 |
о |
9° |
0. 04 |
-4 “ |
604 |
463 |
543 |
|
9 |
-О. 04 |
о |
О |
0 |
622 |
520 |
61 8 |
|
10 |
-О. 04 |
о |
о |
-4 ° |
640 |
518 |
615 |
|
11 |
-О. 04 |
о |
0. 04 |
0 |
653 |
612 |
726 |
|
12 |
-О. 04 |
0 |
0. 04 |
-4 ° |
649 |
603 |
696 |
|
13 |
-О. 04 |
8° |
0 |
0 |
606 |
545 |
648 |
|
1 4 |
-0. 04 |
8° |
О |
-4° |
595 |
545 |
648 |
|
15 |
-0. 04 |
8° |
0. 04 |
0 |
645 |
623 |
745 |
|
16 |
-О. 04 |
8° |
О. 04 |
—4 ° |
643 |
620 |
741 |
На рис. г, з, 4, 5 представлены поля интенсивности напряжений в области паза диска и в хвостовике лопатки для случаев мг и ни - наилучшего и наихудшего, с точки зрения максимальной интенсивности напряжений в диске. Заметим, что наихудший случай характеризуется большой концентрацией напряжений в области контакта, что объясняется уменьшением зоны контакта.
Анализ результатов, представленных в таблице i показывает, что различие между наилучшим и наихудшим случаем по максимальной интенсивности напряжений составляет 14%, по максимальной интенсивности напряжений в лопатке - 43%, по максимальному значению контактных давлений - 42%. Такое различие следует признать достаточно большим, а влияние допусков - весьма существенным.
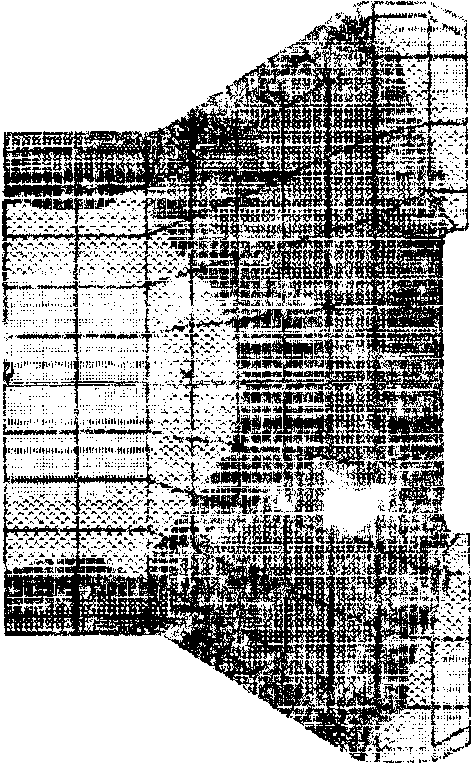

5С Л^в 2^ЛУГУ Ш УУ2Н 36,3840 :32<2355 ТУ.Ю» ^з.йзев 1У.5303 х з ла *6
9.^31
4..Р2Ш 4,2561
Рис.г. Иол® интенсивности пэхгряжея® /кг/ммг/ в хвостовике лопатки для варианта расчета па.

Рио. з Пол© интенсивности напряжений /кг7мм2/ з области паза диска для варианта расчета на,
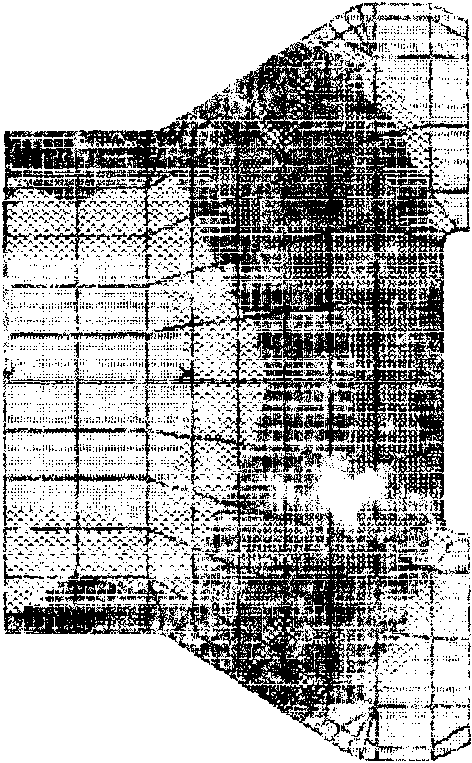

81.2261 55.8861 5@ЛЖ 44,hl'r?
39.ЙЖ ЗЗлСР 26 е91уЗ ”?' Л'7®^ 16.9463 II ,4044 ^8794
Рис.4. Поле интенсивности напряжении /кг/мм2/ в хвоен сеже лопатки для вариам'га расчета нН.

Рис.5. Поле интенсивности напряжений /кг/мм“/ в области
паза диска для варианта расчета ыц.
Для более полного анализа влияние отклонений размеров было решено построить модели этого ахияния на основе регрессионного анализа.
у=£ ЬНЛх) ,
С 1 5
тде у - функция отклика, н^ - базисные функции, ь. неизвестные коэффициенты разложения, х - вектор в пространстве проектирования ст.е. задаваемых факторов). Заметим, что пространство проектирования удобнее представлять в кодированном виде, т.е. по каждому из независимых факторов произвести отражение на отрезок c-i,i>. Тогда, выбрав 4-линейную модель, . ?>жно записать у~Ь +Ь х + Ь х х +Ь х -^Ь х х +Ь х х +Ь х х О 11 2 2 3 3 4 4 522 0 13 7 14
х х +Ь х х +Ь хх т Ь х > ^Ь х х х +
С 22)
8 2 3 Р 2 4 Ю 3 4 11 :" 12 1 2 4
+Ь ххх +Ь ххх -^Ь
X X X X
13 1 3 4 14 2 3 4 15 1 2 Э 4
В результате применения стандартных процедур регрессионного анализа были получены факторные модели для функций отклика , У тдх ,рта,- Коэффициенты уравнения регрессии приведены в таблице 3.
Дальнейшая процедура анализа данных моделей состояла в том, что проводили отбрасывание наименьших коэффициентов модели до тех пор пока относительное отклонение модели от расчетного
Таблица 3.
у =611.875-19,75х -4,625х +15.875х +4,75х х < 3D
1 I тп-^х 1 2 312
у =рл =522,125-51 ,125х +12,5х +4,75х -12,875х х 2 I max 1 3 412
-6.125Х х х 13 4
у . "е,?6 ' - 375~ 40'6875 \ 9 ♦ О625х +5,4375х
1 ё , 5625х х -56,4375.x х +1 3, УбёЗх л
2 13 2
Затем процедуру повторили с тем требованием, чтобы отклонение модели от расчетного значения не превышало 5%. В результате получились модели вада:
с^ -б.! 1 , 875-1 У, 75 х *15,875хС 6?»
с-'1 "522,125-51 . 125х *12,5х -12.875х х -28,75< х *
1 тач 1 3 12£ Э х -12х х х 2 312 3
Р =638.9375-40,6875х -9,O625x -18.5625х х -
-5о.4375х х *13.5625х х *13.4Э75х х х 1 3 2 3"123
Результаты расчета по формулам сзо ,c4i> .се» представлены в ..+,кгхце 4, а результаты расчета по формулам сбо,с7>,с81 в
Г лица 4.
|
max |
я |
Г тих |
|||
|
значения |
ошибка |
значения |
ошибка L- |
. "'наченш? |
ошибка |
|
57е.13 |
0,66810 |
■336,88 |
! 67120 |
7£7>3 3 |
2.00470 |
|
ГГ 1 |
С, 545:38 |
505 3g |
37231 |
681,50 |
|
|
60'7,68 |
0,14415 |
440,38 |
, 261 30 |
5£7♦75 |
0.90822 |
|
50”,88 |
9.02056 |
462,88 |
0. 02759 |
520;8ь |
1 , ЕЭО^бС |
|
576.38 |
О,10832 |
469,13 |
0.67060 |
625,63 |
1,07030 |
|
575,38 |
0,23913 |
437,63 |
0,60345 |
61 0,7'5 |
0 .204 ?f? |
|
608,13 |
0,79527 |
456,63 |
0,08206 |
534.25 |
0,04082 |
|
608,13 |
О.68295 |
459,13 |
1,32290 |
548,13 |
0.94^8 * |
|
625,13 |
О,50241 |
519,63 |
0.07212 |
617.25 |
0,1 2136 |
|
625,I 3 |
2,32420 |
512,63 |
1,03760 |
610,38 |
О , 7’0303 |
|
656,88 |
О,39342 |
61 0,63 |
0, 22467 |
725.13 |
О,О1722 |
|
656,88 |
L . 2.1 340 |
598,63 |
О,72554 |
690,50 |
0;7Q073 |
|
606,38 |
0,06188 |
651,38 |
1 , .1. 6970 |
643,75 |
0,05536 |
|
606,38 |
1,91 1 80 |
544,38 |
0.11468 |
657,63 |
1,48530' |
|
638,13 |
1,06690 |
630,38 |
1,18380 |
7'53,1 3 |
1,09060 |
|
638,13 |
0,7581 G |
618,38 |
0,26210 |
738,25 |
С>, 371 1 2 |
Таблица 5.
|
д |
max |
<у’ |
1 |
р |
|
|
значения |
ошибка |
значения |
ошибка |
значение |
ошибка |
|
576,25 |
О,64655 |
321,1 3 |
4,55590 |
709,31 |
4., 40530 |
|
576,25 |
0,56719 |
; ai ,1з |
3,80980 |
709,31 |
4,00480 |
|
608,ОО |
0,16474 |
446,63 |
0,14013 |
524,31 |
0,25099 |
|
608,ОО |
0,ООООО |
446,63 |
1,40730 |
524,31 |
1,25940 |
|
576,25 |
0,12998 |
453,38 |
2,70920 |
618 ♦ 19 |
О,13120 |
|
576,25 |
0,21739 |
453,38 |
4,22410 |
61 8,19 |
1,011 ОО |
|
608,00 |
0,81566 |
462^88 |
1,28560 |
541,19 |
1,3460>? |
|
608,ОО |
0,66225 |
462,88 |
0,02700 |
541,19 |
0.33379 |
|
615,75 |
1,00480 |
516,13 |
0,74519 |
61 3,81 |
0,67759 |
|
615, 75 |
3, 7891 0 |
516,13 |
0,36197 |
613, 81 |
0.1 9309 |
|
647,50 |
О,84227 |
604,63 |
1,20510 |
708,31 |
2, 436Т? |
|
647,50 |
0,23112 |
604,63 |
0,26949 |
708,31 |
1,7№00 |
|
615,75 |
1,60890 |
547,88 |
0,52752 |
650,69 |
о,41474 |
|
615,75 |
3,48740 |
547,88 |
0,52732 |
660,69 |
0,41474 |
|
647,50 |
0,38760 |
624,38 |
0,22071 |
745,69 |
О,09288 |
|
647,50 |
0,69984 |
624,38 |
0,70565 |
745,69 |
0 Oo^c'S’^ |
Анализ полученных моделей указывает на преимущественное влияние факторов х^ и хд ст.е. отклонений размеров До дан .диска и лопатки) на рассмотренные параметры напряженного состояния замкового соединения. Отклонения размера д практически не оказывают влияния на максимальную интенсивность напряжений в диске и снижают ее значение в лопатке. Таким образом, в случае необходимости усовершенствования конструкции данного замкового соединения, в первую очередь можно рекомендовать ужесточить допускаемые отклонения размера дь.
Вывода:
1.Как показали расчеты, отклонения размеров от номинальных даже в пределах допусков могут весьма существенно влиять на напряженно-деформированное состояние деталей. Поэтому для ответственных элементов конструкций,в частности замковых соединений различных типов и др., можно рекомендовать проводить такую серию расчетов, которые помогли бы выявить это влияние.
г.Предложенная методика расчетов позволяет оценить влияние на напряженное состояние конструкции каждого фактора в отдельности и во взаимодействии с другими факторами. В результате такого исследования можно определить необходимые изменения в конструкции с целью ее оптимизации по напряженному состоянию.


