Моделирование влияния параметров модели тиристора на коммутационные потери в схеме инвертора тока

Современные программы схемотехнического моделирования включают не только поведенческие модели активных электронных компонентов, которые воспроизводят поведение в схеме по электрическим параметрам прибора, но и физические модели, которые построены на уравнениях физики полупроводников и отражают взаимосвязь электрических параметров прибора и физических параметров его структуры. К таким моделям относится и физическая кусочно-зарядовая модель тиристора scr2 [1], входящая в состав программы схемотехнического моделирования «Saber».

В физической кусочно-зарядовой модели scr2 в качестве входных параметров задаются следующие величины:

• 1)    Заряды электронов (qb) и дырок (qbp) в n^--базе при термодинамическом равновесии;

• 2)    Заряды электронов (qgn) и дырок (qg) в p-базе при термодинамическом равновесии;

• 3)    Времена жизни неосновных носителей заряда в n^-- и p-базе (taub и taug, соответственно);

• 4)    Времена пролета носителей через n^-- и p-базу (tp10+tp20 и tp30+tp40, соответственно);

• 5)    Барьерная емкость n^--p перехода при нулевом смещении (cjo2);

• 6)    Отношение объема n^--базы к объему p-базы (fv);

• 7)    Коэффициент сужения обедненной области со стороны p-базы (fj2g);

• 8)    Коэффициент, определяющий, является n^--p переход резким или плавным (mj2);

• 9)    Коэффициент в барьерной емкости n^--p перехода при прямом смещении (fcj2);

• 10)    Максимальное напряжение пробоя n^--p перехода (vj2bk0);

• 11)    Сопротивление, включенное последовательно с анодом (ras);

• 12)    Сопротивление катодного шунта (rsh).

Среди них физическими параметрами полупроводниковой структуры, способными повлиять на коммутационные процессы в тиристоре, являются заряды основных носителей в базах, определяемые уровнем легирования, времена жизни, времена пролета и барьерная емкость. Для того чтобы определить параметры, оказывающие наибольшее влияние на коммутационные потери, была рассчитана мощность коммутационных потерь для тиристора ТБИ173-2000 с номинальными параметрами в схеме инвертора тока (рис. 1).

Рис. 1 Упрощенная схема инвертора тока. В каждом плече инвертора – 4 тиристора.

После этого к каждому из этих параметров, по очереди, давалось приращение в 50% от номинального значения. Затем заново рассчитывалась мощность коммутационных потерь, и вычислялось изменение мощности ΔP kom относительно номинальной. Результаты приведены в таблице 1.

Таблица 1.

Влияние параметров модели на мощность коммутационных потерь

Параметр	qg	qb	taub	taug	tp10+tp20	tp30+tp40	cjo
ΔP kom , %	1.25	-0.417	59.4	10.24	-15.2	3.45	0.0758

Из таблицы видно, что наибольшее влияние на мощность коммутационных потерь оказывает время жизни в n--базе. Кроме него существенно влияние времени жизни в p-базе и времени пролёта n--базы. Время пролета зависит от механизмов переноса заряда (диффузионный или дрейфовый) и определяется формулами [2]:

=W

t, dif   2.D

t

w b

t , drift    ^y

где tt,dif – время пролета, определяемое диффузионным механизмом переноса носителей заряда, tt,drift – время пролета, определяемое дрейфовым механизмом переноса носителей заряда, Wb – ширина n--базы, D – коэффициент диффузии носителей заряда, µ – подвижность дырок, V – напряжение, падающее на n--базе. Таким образом, время пролета определяется, в основном, шириной базовой области и зависит от напряжения, падающего на n--базе. Ширина базовой области в тиристорах сильно изменяться не может, следовательно, не может сильно изменяться и время пролета. Поэтому использовать время пролета для управления коммутационными потерями не имеет смысла.

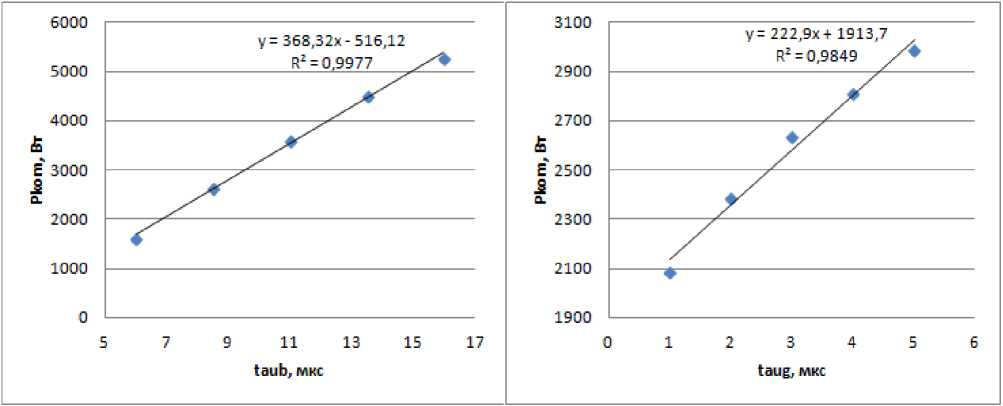
Рис. 2 Зависимость мощности коммутационных потерь от времен жизни в базах тиристора.

Времена жизни неосновных носителей в базовых областях зависят от многих факторов и могут сильно варьироваться. Существуют методы регулирования времени жизни в базовой области [3; 4; 5]. Поэтому изменение времени жизни в базовых областях тиристоров можно использовать для контроля мощности коммутационных потерь. Зависимость мощности коммутационных потерь от времён жизни неосновных носителей в базовых областях приведена на рис. 2.

Влияние времени жизни на коммутационные потери обусловлено тем, что именно время жизни определяет максимальный накопленный заряд в базовой области [6]. В свою очередь, от максимального накопленного заряда и скорости спада тока, в первом приближении, будет зависеть заряд обратного восстановления Q rr , который во многом определяет коммутационные потери. Зависимость заряда обратного восстановления от времен жизни в базах приведена на рис. 3. Из графика (рис. 3) видно, что угловой коэффициент зависимости Q rr (taug) меньше, чем угловой коэффициент зависимости Q rr (taub), приблизительно на 40%. Такое же соотношение имеют угловые коэффициенты зависимостей P kom (taub) и P kom (taug) (рис. 2). График зависимости P kom (Q rr ) приведен на рис. 4.

При последовательном соединении тиристоров немаловажную роль играет разброс параметров. Время жизни в n^--области может различаться даже у тиристоров из одной партии, что, в свою очередь, означает наличие разброса Q rr и связанного с ним разбаланса напряжений тиристоров в последовательном соединении [7]. Разбаланс напряжений, в свою очередь, приводит к тому, что в тиристорах выделяется разная мощность коммутационных потерь. При этом возникает разница температур тиристоров, которая может повлиять на параметры приборов, зависящие от температуры, и срок службы и надежность тиристоров.

Для определения максимальной разницы температур в тиристорах в последовательном соединении был определён худший случай, когда разброс Q rr приводит к максимальному разбалансу обратных напряжений при коммутации в плече инвертора тока (рис. 1). Это случай наблюдается тогда, когда один из четырех тиристоров имеет минимальный заряд обратного восстановления в диапазоне, заданном разбросом Q rr , в то время как остальные тиристоры – максимальный.

Определить разницу температур можно, предполагая, что тепловые сопротивления переход-корпус тиристоров в последовательном соединении одинаковы. Тогда:

A T \ P • R th ( j - c ) (2)

В уравнении (2) ΔT – разница температур кристаллов тиристоров в последовательном соединении, ΔP – наибольшая разница мощностей между тиристорами последовательного соединения, R th(j-c) – тепловое сопротивление переход-корпус тиристоров.

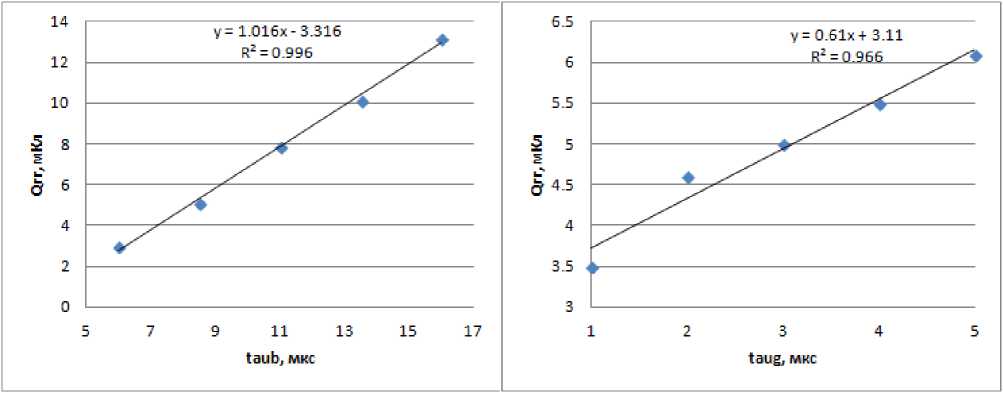
Рис. 3 Зависимость заряда обратного восстановления от времен жизни в базовых областях тиристора.

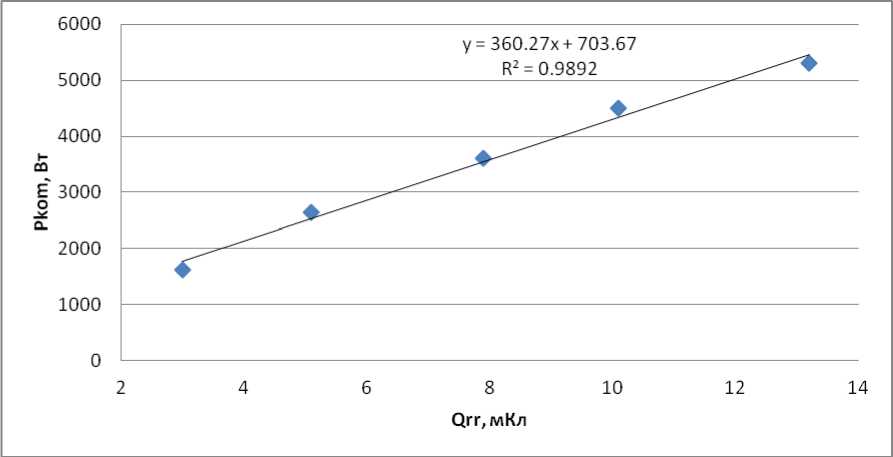
Рис. 4 Зависимость мощности коммутационных потерь от заряда обратного восстановления

В тиристорах одного плеча инвертора тока (рис. 1) для худшего случая были рассчитаны средние мощности потерь за период при разбросе Qrr, равном 5%, 10% и 15%. Далее по известному из справочных данных температурному сопротивлению переход-корпус Rth(j-c) тиристора была рассчитана максимальная разница температур тиристоров в последовательном соединении. Тепловое сопротивление кристалл-корпус тиристора равно 0,008 °С/Вт для двухстороннего охлаждения и 0,016 °С/Вт – для одностороннего [8]. В таблице 2 приведены результаты расчётов для случаев одностороннего (ΔTOSC) и двухстороннего (ΔTDSC) охлаждения приборов.

Таблица 2.

Разница температур тиристоров в последовательном соединении при различных значениях разброса Q rr

Разброс Q rr , %	5	10	15
ΔT OSC , °C	8,18	15,7	23,6
ΔT DSC , °C	4,09	7,85	11,8

Из значений, приведённых в таблице 2, можно заключить, что зависимость разницы температур кристаллов тиристоров от разброса Q rr близка к линейной с угловым коэффициентом, приблизительно равным 0,8 (для ΔT DSC ) или 1,6 (для ΔT OSC ) °С/%.

На практике достаточно сложно подобрать группу тиристоров с разбросом Q rr менее 10%. Кроме того, из-за несовершенства технологии производства возможно наличие разброса тепловых сопротивлений тиристоров в последовательном соединении. В этом случае разница температур может быть ещё больше.

Таким образом, получены следующие результаты:

• 1.    Установлено, что наиболее сильное влияние на мощность коммутационных потерь в тиристорах в схеме инвертора тока оказывает время жизни носителей заряда в n^-базовой области тиристора.

• 2.    Из результатов моделирования получены следующие угловые коэффициенты зависимости зарядов обратного восстановления от времен жизни носителей заряда в базовых областях тиристоров ТБИ173-2000 К Qrr (taub)= 1016 Кл/с и К Qrr (taug)= 610 Кл/с, а также угловые коэффициенты зависимости мощности коммутационных потерь от времен жизни К Р (taub)=0,386 Вт/мкс, К Р (taug)=0,223 Вт/мкс и угловой коэффициент зависимости мощности коммутационных потерь от заряда обратного восстановления К Р (Q rr )=0,36 Вт/мкКл.

• 3.    Разброс заряда обратного восстановления тиристоров при их последовательном соединении приводит не только к перенапряжениям на тиристорах с меньшим зарядом обратного восстановления, но и к повышенной мощности коммутационных потерь на них. Увеличение разброса Q rr в схеме инвертора тока (рис.1) способно стать причиной

существенного перегрева тиристора с меньшим зарядом обратного восстановления относительно других. При одностороннем охлаждении тиристора и разбросе Q rr 15% перегрев может доходить до 23,6 °С. Таким образом, высокий разброс Q rr тиристоров в последовательном соединении при недостаточном охлаждении способен стать причиной выхода тиристоров из строя.