Моделирование внутрифирменных денежных потоков интегрированной группы предприятий

Автор: Димитриев А.М., Вишникина А.А., Внуков И.А.

Журнал: Вестник Алтайской академии экономики и права @vestnik-aael

Статья в выпуске: 9-2, 2020 года.

Бесплатный доступ

Важным резервом роста рыночной эффективности крупных промышленных корпораций и интегрированных бизнесов является совершенствование планирования и управления их денежными потоками, что способствует сокращению производственных и непроизводственных затрат и снижению рисков внутрифирменного оппортунизма. Целью данной работы является разработка и практическая адаптация инструментария экономико-математических моделей и методов оптимального управления внутрифирменными денежными потоками интегрированной группы предприятий на последовательности временных интервалов, составляющих среднесрочный горизонт планирования. Обоснован выбор эндогенных и экзогенные переменные модели, критериев оптимальности и системы ограничений. Динамический вариант модели использован для анализа и управления денежными потоками пяти предприятий и управляющей компании, образующих интегрированную группу. Полученные результаты моделирования денежных потоков для различных вариантов организации внутрифирменных трансфертов, выбора ставок внутрифирменного кредитования и предельных уровней риска структуры капитала предприятий группы позволили положительно оценить адекватность предложенного инструментария реальной практике функционирования крупных предприятий и холдинговых объединений. В частности, нашел подтверждение факт положительного влияния роста риска структуры капитала предприятия в составе интегрированной группы на эффективность его производственной деятельности и рост централизованного инвестиционного фонда объединенной компании.

Еще

Производственная корпорация, интегрированная группа предприятий, структурная бизнес-единица, неоклассическая производственная функция, денежный поток, модель оптимизации денежных потоков, критерии оптимальности

Короткий адрес: https://sciup.org/142225358

IDR: 142225358 | DOI: 10.17513/vaael.1326

Текст научной статьи Моделирование внутрифирменных денежных потоков интегрированной группы предприятий

An important reserve for the growth of market efficiency of large industrial corporations and integrated businesses is to improve the planning and management of their cash flows, which helps to reduce production and non-production costs and reduce the risks of intra-company opportunism. The purpose of this work is to develop and practically adapt tools of economic and mathematical models and methods of optimal management of intra-company cash flows of an integrated group of enterprises on a sequence of time intervals that make up the medium-term planning horizon. The choice of endogenous and exogenous variables of the model, optimality criteria and system of restrictions is justified. The dynamic version of the model is used to analyze and manage the cash flows of five enterprises and a management company that form an integrated group. The obtained results of cash flow modeling for various options for organizing intra-company transfers, selecting intra-company lending rates and limiting risk levels of the capital structure of the group’s enterprises allowed us to positively assess the adequacy of the proposed tools to the actual practice of functioning of large enterprises and holding associations. In particular, it was confirmed that the increase in the risk of the enterprise’s capital structure as part of an integrated group has a positive impact on the efficiency of its production activities and the growth of the centralized investment Fund of the combined company.

Состояние российской экономики во многом зависит от эффективности рыночной деятельности крупных производственных компаний и вертикально-интегрированных холдингов. Это актуально как для корпоративного, так и для государственного сектора. Интегрированные производственные структуры имеют явное преимущество в виде синергии, достигаемой в результате взаимодействия бизнес-единиц в рамках интегрированной группы предприятий (ИГП). Поэтому первостепенное значение имеет оптимизация денежных потоков внутри фирмы, организация рациональной логистики материальных и денежных средств между управляющей компанией и подразделениями ИГП.

Проблема управления денежными потоками независимых агентов рынка освещалась в отечественных и зарубежных исследованиях. Среди последних работ по данной тематике следует выделить исследования профессора Халикова М.А., а также его учеников [21, 22, 24, 28]. В работах [28] и [2] рассматривается проблематика оптимизации внутрифирменных хозяйственных связей крупных производственных корпораций и холдингов.

Целью данного исследования является разработка и адаптация экономикоматематических моделей оптимизации денежных потоков холдинга с учетом существующих ограничений и приоритетов в операционной сфере бизнес-единиц в его составе.

Теоретической основой работы послужили исследования отечественных и зарубежных ученых: А. Алчя-на и Х. Демсеца [1], И. Ансоффа [3], Г.Б. Клейнера и его учеников [15, 16], И.Г. Владимировой [10], В.О. Ивановой [12], Б.А. Логоши и его учеников [18], М.А. Халикова и его учеников [21, 22, 25, 26, 28, 33], Ю.В. Якутина [31]. Модели «выпуск – затраты» рассмотрены в работах: Г.Б. Клейнера [14], В.А. Ко-лемаева [17], Д.А. Безухова и М.А. Халикова [4, 9, 24, 27, 29]. Численные методы решения оптимизационных задач в непрерывной и дискретной постановках рассмотрены в работах М. Аоки [5], Н.С. Бахвалова [7], М.А. Горского [11], Н.Н. Моисеева [20], М.А. Халикова [23], А.С. Немировского [30].

Теоретические аспекты. Денежные потоки операционной (производственной) сферы i-ого СБЕ холдинга на временном интервале t.

Производственный холдинг – объединение субъектов рынка под руководством управляющей компании. Структурные бизнес-единицы (СБЕ) взаимодействуют посредством общих материальных и денежных потоков. Такая взаимосвязь – следствие единства целей и взаимовыгодного сотрудничества СБЕ интегрированной группы в сферах рыночной деятельности: операционной (производственной), финансовой и инвестиционной.

Движение денежных средств регламентируются стандартами финансовой отчетности, в частности, МСФО. В область ответственности управляющей компании входит планирование и управление в операционной сфере, осуществление инвестиций из средств СБЕ, привлеченных кредитов со стороны внешних у финансовых учреждений и общефирменных средств инвестиционного фонда. Управляющая компания (УК) перечисляет трансферты в адрес СБЕ, которые являются низко рисковым и малодоходным со финансированием рыночной деятельности подразделений. Цель трансфертов – повышение рентабельности собственного капитала СБЕ при устойчивом спросе на ее продукцию. Трансфертные кредиты оказываются «дешевле» других видов заемного финансирования. УК получает от СБЕ также дополнительные средства за предоставление трансфертного кредита для покрытия рисков и операционных затрат. За счет этого происходит и пополнение централизованного фонда ИГП.

Определим основные понятия, используемые в работе. Рабочий капитал – постоянные и переменные активы СБЕ, создающие новую стоимость в процессе производства. Активы списываются на счета соответствующих видов затрат. Сюда входят также собственные и привлеченные средства, покрывающие затраты производственной деятельности. Рабочий капитал на определенном цикле операционной деятельности представляется в виде затрат, которые восстанавливаются из валового продукта.

Функция «затраты – выпуск»- аналитическая зависимость между величиной рабочего капитала СБЕ в виде затрат и максимальным объемом реализуемой на рынке продукции (в стоимостном выражении). В работе в качестве примера используется неоклассическая производственная функция.

Определим соотношения, устанавливающие баланс движения денежных средств производственного сегмента i-й СБЕ в плановом интервале t:

PK^ = W _ + InV — , (1) где t – индекс планового пер ио да (t = 0, T ); i – индекс СБЕ (i = 1, I ); PK t¹ ¹ - объем рабочего капитала i-ой СБЕ в начале интервала t; W _t ⁽ ¹ ¹ - объем затрат рабочего капитала i-й СБЕ, покрытых из валовой выручки периода t; Inv t ¹ - величина денежного потока собственных инвестиций в рабочий капитал производственной сферы i-ой СБЕ по в начале интервала t;

2а^ < PK^ ; (2)

X^ min { F ¹ ¹ ¹ ( t ; Z t ) ) , Sp ^H} , (3)

где X ti - выпуск продукции i-й структурной бизнес-единицы (в дальнейшем СБЕ) на интервале t; F ⁽ ⁱ ⁾ ( t ; Zat t¹ ) ) -производственная функция СБЕ, определяющая зависимость между максимальным объемом выпуска производственного сегмента и затратами ресурсов в стоимостном выражении; Zat t¹ ¹ - затраты производственной сферы i-й СБЕ на интервале t (сюда входит и амортизация постоянного капитала, списываемая на результаты производственной деятельности этого периода); Sp t ¹ - рыночный спрос (в стоимостном выражении) на продукцию i-й СБЕ в плановом периоде t;

N^ = т<Х^ -W^V где т - ставка налога на прибыль; Nt11 -денежный поток выплат по кредитам, налогам и прочим обязательным платежам; – объем краткосрочного кре-

дита, взятого на пополнение рабочего капитала; p – ставка по кредитам для СБЕ; ^t

К »₌ X ¹ N t¹ ) , (5) где K t¹ - остаточный доход (конечный продукт), сформированный в производственной сфере i-ой СБЕ на интервале t;

D^ ¹ + Z^ + SI^ K ¹ , (6) где D t¹ ¹ - объем непроизводственного потребления i-ой СБЕ по завершении интервала t; Z¹¹ - величина денежного потока средств, передаваемых в централизованный инвестиционный фонд холдинга по завершении интервала t; Si t¹ - денежный поток собственных инвестиций в рабочий капитал СБЕ по окончании интервала t;

Z t°> ( 1 + ^ f¹ ) - TR t¹ , (7) где TR ¹'¹ - объем трансфертов, перечисленных в адрес УК холдинга i-й СБЕ в начале периода t; dt'¹ - ставка по внутрифирменным трансфертам;

Zat t¹ , W¹ ¹ ,D t ⁰, SI_t ^(/1 > 0; (9)

PK (^ rk H , (10) где RK H - объем рабочего капитала СБЕ в конце нулевого периода.

Выделим эндогенные (управляемые) параметры модели управления денежными потоками производственного сегмента СБЕ:

– объем заемного капитала , идущего на увеличение рабочего капитала;

- объем активов Zat_t ^{( 1} в составе рабочего капитала, покрывающий постоянные и переменные затраты производственной деятельности в период t;
- объем отчислений D _t ^{( 1} на непроизводственное потребление по окончании периода t;
- объем средств Z_t ^{( 1} , передаваемых по окончании периода t в централизованный инвестиционный фонд ИГП.

Денежные средства, перечисляемые в адрес УК, способствуют увеличению инвестиций в рабочие капиталы СБЕ.

Соответственно, растет и централизованный инвестиционный фонд. Установим балансовые соотношения для обратных денежных потоков, формирующие централизованный инвестиционный фонд холдинга:

I i TR ( i ) t - 1 ;

i = 1

× (12)

Q t > 0, t = 1, T , (13)

где Ω _t- ₁ , Ω _t – объемы централизованного инвестиционного фонда на конец интервалов t-1 и t; – ставка по размещенным на банковском депозите средствам централизованного инвестиционного фонда ИГП на временном промежутке t.

Ограничения (12), (13) устанавливают возможность реализации финансовой деятельности как для УК, так и для рассматриваемых СБЕ.

Все вышеприведенные соотношения отвечают заявленным предпосылкам динамической модели денежных потоков структурных подразделение ИГП.

В качестве критерия оптимальности управления внутрифирменными денежными потоками ИГП можно выбрать дисконтированный за период управления суммарный денежный поток остаточного дохода, распределяемый из производственных сегментов СБЕ на производственное и личное потребление:

T 7+1

7=1 7=1

где i = I + 1 – индекс УК, остаточный доход которой в период t составляет объем средств, соответствующий изменению централизованного инвестиционного фонда (знак «+» означает рост, «-» – снижение); e – ставка дисконтирования для альтернативной доходности с обс твенного капитала в интервал t (t = 1, T ).

Таким образом, динамическая модель оптимизации денежных потоков

ИГП в формализованном виде на интервале [1;T] включает:

– внутрипериодные ограничения (1) – (10);

– межпериодные ограничения (11) – (13);

– интегральный критерий (14) оптимальности, представленный как дисконтированный к началу рассматриваемого периода суммарный по всем СБЕ поток остаточного дохода.

Заметим, что ограничение (9) может быть расширенно ограничением также на целочисленность эндогенных переменных и наборов Xt¹ ) для дискретного варианта модели. Если рассматривать дискретный вариант, то в соотношении (3) нужно брать целую часть от правой части выражения.

Заметим также, что остаточный доход Kt¹ ) распределяется на непроизводственное потребление D ti ) , пополнение централизованного инвестиционного фонда Z ti ) и собственные инвестиции Si ti ) в рабочий капитал. Тогда баланс денежных оттоков i-й СБЕ задается выражениями:

D ti = a ( J ■ K i ; Z_t ⁽ ⁱ ⁾ = ag ■ K i ;

SI t ^M= (1 - a! it -0 2 , ) K (15)

a *i ',a 2 t e[ 0;1 ] ; a l it + a^ < 1, ⁽¹⁶⁾

где a * i ) , a ⁽ ₂ i\ - нормы распределения остаточного дохода СБЕ на, соответственно, непроизводственное потребление и пополнение централизованного фонда ИГП на временном промежутке t.

Введем индекс I + 1 для УК и воспользуемся коэффициентами r I + _1t (i = 1, I ), обозначающими доли трансфертных отчислений в рабочие капиталы СБЕ:

ТР1 i) 1 i) . (ГР)1+1)- 7 rI+1, t t ^ (17) I Ir!)1,t=1; i=1 (18) ri(+1,t e[0;1], (19) где TRt1+1) - объем средств из централизованного инвестиционного фонда

ИГП Ω _t _-1 на конец предшествующего интервала;

Установим зависимость между нормой a t распределения остаточного продукта, долей трансфертных отчислений r^!, _t из централизованного инвестиционного фонда в СБЕ, величиной трансфертов TR t¹ ⁺ ¹ ⁾ и ставкой трансфертного кредитования dt¹ ⁾ .

Из зависимостей (7), (15) и (16) получим:

ag ■ K i > ( 1 + df ) ■ r I + 1, _t ■ TR t¹ ⁺ ¹ ⁾ (20)

или с учетом очередности установления внутрифирменных нормативов:

траты (на единицу выпуска) рабочего капитала СБЕ.

Отсюда получим соотношение:

X ( t ) =

f Zat t¹^’

I c ( 1 ) J •

Для упрощения будем полагать, что в неравенстве (2) весь производственный капитал полностью авансируется в затраты. В этом случае рост объемов производства ведет к росту объемов реализации и маржинального дохода.

Следовательно, соотношение (24) можно представить в виде, соответствующем соотношению (3) для неоклассической производственной функции:

( i ) 2, t

> min ( 1;

( 1 + 4 ' 1 r I +1, t ■

K t¹

TR ^¹ ⁺ ¹ ⁾

. (21)

X* =

f PKti)7, . c, (1)>

Тогда ограничение (11) можно представить в виде:

TR t¹ ⁺ ¹ ⁾< Q _t -1 .

Теперь мы можем заменить эндогенные параметры TR t¹ ¹ , D t¹ ¹ и Z t¹ ¹ ^на ^a ⁽ it ^, a .^, r I + 1, t .

Рассмотрим неоклассическую зависимость для функции «затраты-выпуск», чтобы оценить влияние эндогенных переменных на состав и объемы денежных потоков производственных сегментов СБЕ:

Zat t¹ ¹ = C i ( 1 ) -( A : )^ , (23)

где γ – степень однородности функции «затраты-выпуск»; c (1) – удельные за-

Зависимость между краткосрочными заимствованиями СБЕ и собственным капиталом, задается коэффициентом автономии в⁽ ¹ ⁾ (коэффициент риска структуры капитала):

SI^+TR^ + ЗК^

где Sj t'X - собственные инвестиции в рабочий капитал i-й СБЕ в конце периода t-1;

TR ti - трансферты УК в рабочий капитал СБЕ в начале периода t;

– краткосрочный кредит, выделяемый СБЕ в начале периода t.

Коэффициент в t ^ примем в качестве эндогенного параметра. Тогда объем краткосрочного кредита можно представить как:

или

ЗК^

а-рмуся217«22

(1 -13«) - ((1 - а« , - а?>,) - ^ 7^

ри

С помощью соотношений (8) и (26) запишем выражение для 'nv ' (инвестиции в рабочий капитал) в виде:

inv ' = Si^ + TR ' ' +

1 -в!'1 в !"

■( Si*1+ TR*) =

=4т■ ( S' ( 'V TR 4 = 4т■((1 -а ( ' ) ,-а® ,)■ K ( ' ) + r !?„ ■ TR ⁽ ' + ¹ ¹). ( ' ) t ^- ¹ t ( ' ) 1, ! -1 2, ! -1 ^! ^- ¹ ' ⁺ ^1, ^{! !}

С учетом полного расходования рабочего капитала структурной бизнес-единицей в затратах производственной деятельности и его дальнейшем восстановлении баланс производственных активов на интервалах t-1 и t примет вид:

РК^ = PK^^ + inv ' . (30)

Опишем алгоритм моделирования экономической деятельности ИГП на временном промежутке [0; T], где T – стратегический горизонт планирования и оценки денежных потоков УК и С БЕ .

УК в начале интервала t (t ∈ 1, T ) устанавливает объем централизованного инвестиционного фонда ИГП в соответствии с выражением (11), далее определяется допустимый объем внутрифирменных трансфертов TR !' ⁺ ¹ ⁾ по соотношению (22).

По алгоритму, представленному в работе [2], определяются r ' + ' 1, _! (доли отчислений в СБЕ) в соответствии с выражениями (18) и (19). Поступления трансфертов в рабочие капиталы СБЕ вычисляются в соответствии с соотношением (17).

Далее находится допустимый объем краткосрочных кредитов с учетом выбранного коэффициента в ! '' на уровне i-го (i = 1,I) СБЕ в начале периода t. Затем вычисляется общий приток инвестиций в производственную сферу СБЕ по формуле (29).

На следующем шаге последовательно определяются основные параметры производственной деятельности i-й СБЕ на производственно-коммерческом цикле, соответствующем интервалу t: величина рабочего капитала (формула (1)); объем валового выпуска х !' (формула (23)); объемы налоговых платежей, других вычетов N ' ' (формула (4), значение задается (26)) и остаточного дохода K !' ' (формула (5)).

Каждая СБЕ в конце периода t устанавливает доли остаточного дохода а ⁽ ^! ) и а^ , направляемые на непроизводственное потребление и в централизованный инвестиционный фонд ИГП, соответственно. Объемы оттоков из остаточного дохода вычисляются по формулам (15), а значения долей ограничиваются соотношениями (16).

Нулевому временному интервалу будут соответствовать: TR!'+1' = 0; Q0 = N9 (здесь Nθ – объем взносов учредителей холдинга на момент его организационно-правового основания); , (i = 1,I) ( – начальная величина рабочего капитала i-й СБЕ).

Таким образом, динамика внутрифирменных денежных потоков ИГП на промежутке [0;T] задается: приве-

денными значениями их величины для нулевого периода; эндогенными параметрами TR1;'+1),г'+1,!,р!'', «('^,а2°!, (i = 1,1), значения которых устанавливаются управляющей компанией и структурными подразделениями в начале и по окончании очередного периода t, (! = (1, T) (их значения регулируются зависимостями (15), (16), (18), (19), (21), (22)).

В описании динамики результатов производственной сферы СБЕ, экзогенными переменными выступают показатели функции «затраты-выпуск» γ _i и C_i (1), ставки τ (налога на прибыль) и ρ _t (кредитная) не.

Чтобы привести показатели, выражающиеся в стоимостном виде, к общей системе измерений, определим еще один параметр, обозначающий финансовый результат (валовой доход), получаемый в производственной сфере СБЕ:

_KD( ' ) = р _! (' ) . х !' , (31)

где X ⁽ ¹ ⁾ - валовой выпуск i-й СБЕ на интервале t; P_! ' - рыночная цена единицы продукции i-й СБЕ.

После введения понятия финансового результата VD ^i ) нужно уточнить уравнения (4) и (5). На место переменной X ti ) следует поставить VD ti ) .

Эмпирические расчеты по динамической модели оптимизации внутрифирменных денежных потоков ИГП.

Рассмотрим следующий контрольный пример:

– расчет денежных потоков структурных подр аз делений холдинга для 5-ти СБЕ (i = 1,5) на горизонте планирования, равном десяти интервалам: t = 1,10;

- значения коэффициента в ti ) = 0,2; 0,4; 0,6; 0,8;
- для каждого значения P t ^!) = const и для каждого с труктурного подразделения (i = 1,5) последовательно рассчитать:

1) K ti ) - остаточный доход i-й СБЕ (конечный продукт);
2) Z ti ) — денежный поток средств, передаваемых УК в централизованный инвестиционный фонд;
3) – эффективность средств, вложенных в рабочий капитал.

– построить графики для каждого из значений p t ^!) и оценить результаты проведенных расчетов. Для УК на графике отметить Ω _t и эффективность трансфертных отчислений в рабочие капиталы подразделений:

(t = 1,10).

Приведем данные, исходя из которых рассчитывались денежные потоки, результаты производственной деятельности и эффективность средств, вложенных в рабочий капитал.

I = 5, (i = 6 – индекс УК),

Sp _i ^(t) – произвольное большое число, не лимитирующее объем производства.

Таблица 1

Значения экзогенных параметров

i	ɤ	C(1)	P	^ρ	τ	d	^ϕ	f
1	0,6	1,2	2,0	0,18	0,2	0,16	0,03	0,06
2	0,8	1,3	2,1	0,18	0,2	0,16	0,03	0,06
3	0,8	1,3	2,2	0,18	0,2	0,16	0,03	0,06
4	0,8	1,3	2,2	0,18	0,2	0,16	0,03	0,06
5	0,9	1,3	2,3	0,18	0,2	0,16	0,03	0,06

Таблица 2

Значения эндогенных параметров

i	r	^α1,i	^α2,i
1	0,2	0,2	0,3
2	0,1	0,2	0,3
3	0,1	0,2	0,4
4	0,1	0,2	0,4
5	0,1	0,2	0,4
УК	0,4

Данные табл. 1 и 2 актуальны для всех временных интервалов t.

Также для начального периода (t = 0) известно:

Таблица 3

Объемы рабочего капитала СБЕ и средств централизованного инвестиционного фонда ИГП в нулевом периоде

i	PK	Ω
1	136	500
2	142	500
3	144	500
4	146	500
5	148	500

Результаты вычислений

С учетом перечисленных выше формул и первоначальных данных рассчитаны все показатели для пяти структурных бизнес-единиц на протяжении десяти последовательных временных интервалах при различных уровнях риска структуры капитала, а также коэффициенты эффективности рабочих капиталов для всех СБЕ и управляющей компании.

Для первой СБЕ при любых показателях риска структуры капитала не будет производиться ненулевой конечный продукт на всем временном промежутке. Это также свидетельствует о нулевой эффективности средств, вложенных в рабочий капитал этой структурной бизнес-единицы.

При первая СБЕ будет производить промежуточный продукт, а при показателе риска 0,2 объем производимой конечного продукта пойдет на спад после 5-го раунда (рис. 1). Это вызвано значительным ростом объема краткосрочного кредита, который превышает увеличение валового дохода этой СБЕ (рис. 2).

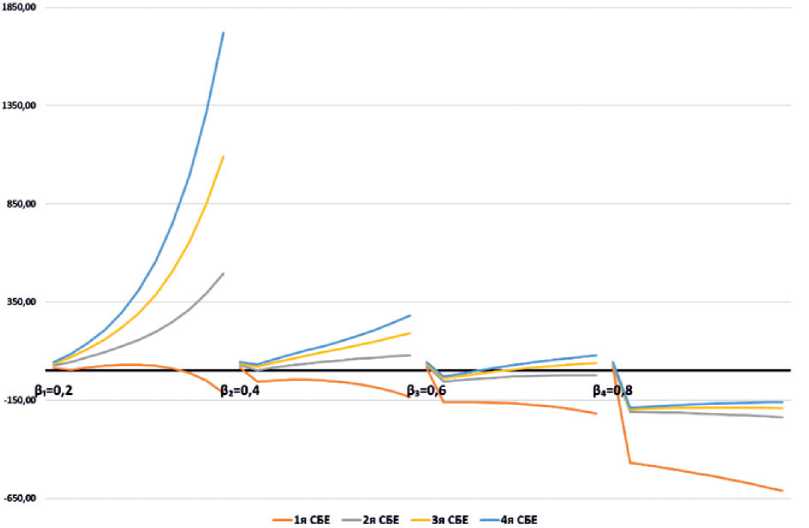
Рис. 1. Динамика промежуточного продукта для первых четырех СБЕ при различных показателях риска структуры рабочего капитала

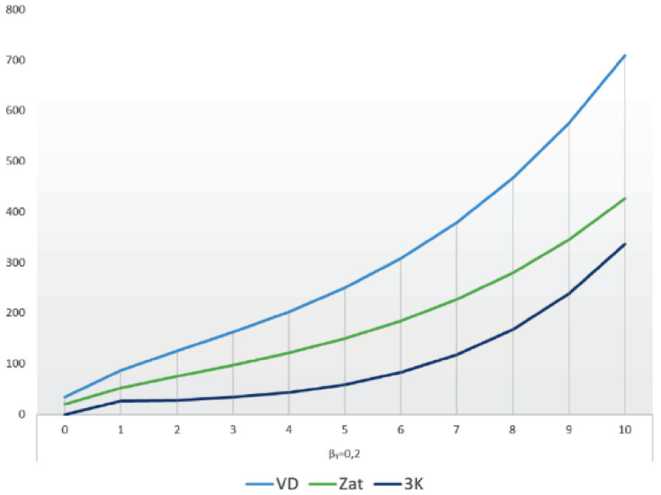
Рис. 2. Валовой доход, затраты на производственную деятельность и краткосрочный кредит первой структурной бизнес-единицы при коэффициенте риска 0,2

Рассмотрим вторую структурную бизнес-единицу. Здесь также при всех значениях показателя риска на выбранном интервале не будет появляться конечная продукция. При pi(t) = 0,2; 0,4 это вызвано тем, что объемы промежуточного продукта меньше, чем сумма налогов и трансфертов на погашение внутрифирменного кредита. В двух других случаях не будет произведено даже промежуточного продукта.

Для третьей СБЕ возможно иметь ненулевой конечный продукт при коэффициенте риска структуры капитала 0,2 (рис. 3).

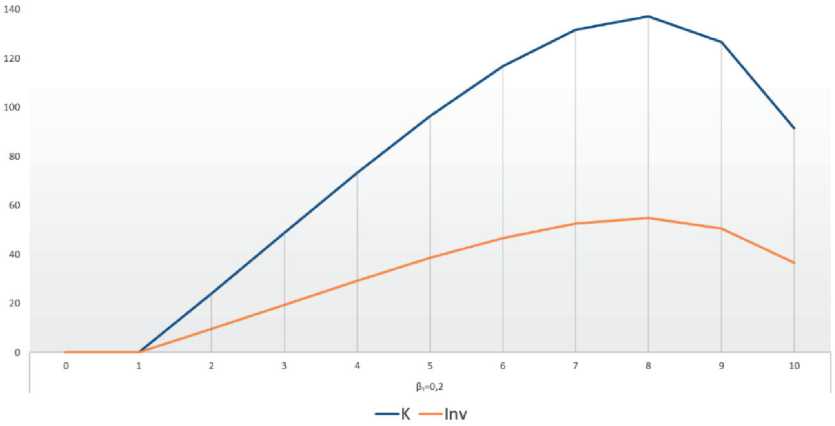
Рис. 3. Динамика конечного продукта и инвестиций в рабочий капитал третьей СБЕ при коэффициенте риска структуры 0,2

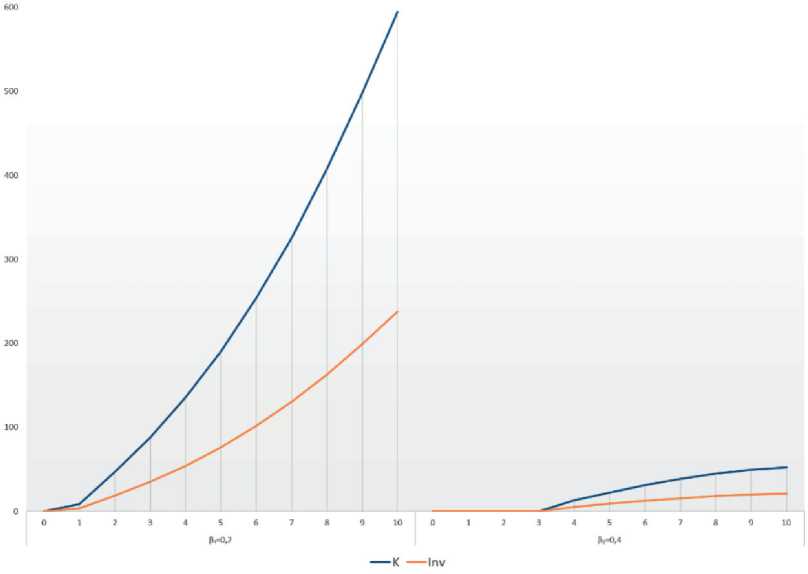
Рис. 4. Динамика конечного продукта и инвестиций в рабочий капитал четвертой СБЕ при коэффициентах риска его структуры 0,2 и 0,4

Однако значительное увеличение трансфертов, перечисляемых управляющей компании на погашение внутрифирменного кредита, после пятого раунда привело к снижению объемов конечного продукта, а после 8-го раунда динамика становится нисходящей как для конечного продукта, так и для непроизводствен- ного потребления и инвестиционных отчислений, зависящих от них напрямую.

Для четвертой структурной бизнес-единицы, несмотря на незначительные различия в исходных данных по сравнению с третьей СБЕ, динамика будут благоприятной как для pi(t) = 0,2, так и 0,4 (рис. 4). В первом случае объемы конечного продукта будут значительно расти с каждым раундом, а при большем риске они будут увеличиваться равно замедлено.

При этом эффективность средств, вложенных в рабочий капитал, будет больше при наименьшем коэффициенте риска как для данной СБЕ, так и для управляющей компании (рис. 5).

Рассматривая пятую структурную бизнес-единицу, следует отметить, что у нее наилучшие показатели при наименьшем риске среди всех рассмотренных СБЕ. У нее самая высокая эффективность средств, вложенных в рабочий капитал, что соответствует наибольшему выпуску продукции и объему конченого продукта. Также эта СБЕ получает положительные результаты при коэффициенте риска, равным 0,4 и 0,6, однако в этих случаях показатели эффективности значительно ниже.

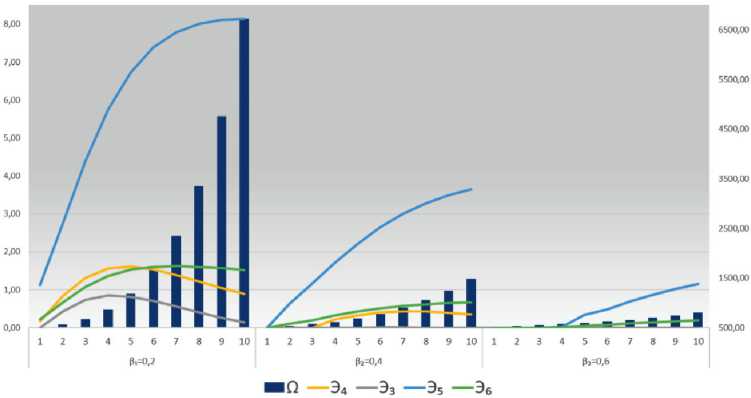
Рис. 5. Динамика эффективности вложенных средств и объемов средств централизованного инвестиционного фонда ИГП для 3-й, 4-й и 5-й СБЕ, а также УК

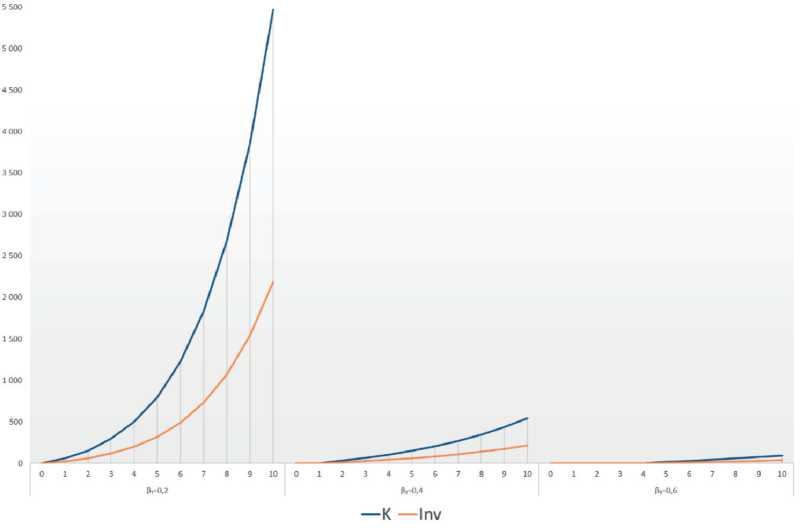
Рис. 6. Динамика конечного продукта и инвестиций в рабочий капитал пятой СБЕ при коэффициентах риска его структуры 0,2; 0,4 и 0.6

Результаты проведенных расчётов представлены в таблицах 4-9.

Таблица 4

Показатели для первой СБЕ

РК

Pr-N-TR*(l+di)

шп 1пу|э

517,60 ; 103,52 ; 649,52 ; 43,66 ; 87,31 ; 52,39 ; 25,88 ; 4,39 ;0,88; -116,57 ; 0; 0 ; 0;

562,49 i 112,50 i 1192,52 j 62,86 |125,72 | 75,43 j28,12

672,60 i 134,52 i 1829,34 i 81,26 j 162,52 j 97,51 i33,63

868,9 F 173,8 Г 2 643,4 1 101,з1 202,7 7 121,6 Г 43,4I

1 182,67! 236,53 I 3 746,76 ! 12'4,94! 249,8?! 149,92"! 59,13|

1657,56 Г 331,51 Г5 291,91 ■ 153,691 307, Зэ7184,43 Г82,88

17,10 13,42 ; -116,82 ; о; о; о; о ; о 25,32 i 5,Об! -135,78 j 0 j о" j б j 0 j О 29,8 1 6,0 I -17'7,7" 1 о Го 767 о 7 о 30,17 1 6,03! -250,24 1 оТо'ТбТ 0"7"0

2 353,69; 470,74 ; 7 486,85 ; 189,27 ; 378,53 ; 227,12 ; 117,68 ; 12,54

-364,43 ' 0 ' 0'0 '

-536,02 ^рГр^О^

3 352,23 i 670,45 |10 614,47 | 233,36 | 466,72 | 280,03 | 167,61| -11,09 j 0,00| -788,81 | 0 | 0 | 0 | 0 | 0 4 761,20 1 952,24 i15 057,24 i 287,83 i 575,66 i 345,40 i 238,06 i -50,65 i 0,00i -1155,24 | 0 i 0 i 0 i 0 i 0 6 722,75 F1344,55 pl328,28 ] 354,7ol 709,417425,64 i~336,141 -112,881 0,00] -1672,56 1 0 ГоТрТ Q 7 Q

517,60 ! 103,52 ! 304,45

535,82 Г 107,16 Г 473,93

554,68 : 110,94 ; 644,60

РК I X | VD | Zat | ЗК | Pr I N~[ Pr-N-TR*(Hdi) 020 I nv IЭ

27,71 ! 55,42 I 33,25 I 155,28 36,Гз1 72,27 7 43,36 7160,75 43,46j 86,92 7 52-15 Пбб,40

574,21 [ 114,84 'L 816,67 j 50,09J 100,17_[ 60,10 [172,26

595,05 i 119,01 i 990,52 623,94 F 124,79 Г1168,78 657,99 Г 131,60 71 353,04 699,51 ! 139,90 ! 1545,62 748,15 ! 149,63 71748,64 805,05 Г 161,01 Г1964,53

56,24 i 112,47 i 67,48 j 178,51 62,111 124,217 74,53 Г187.18 67,811 135,627 81,37 Г197.40 73,44 ! 146,89 j 88,13 j 209,85 79,091 158,187 94,91 7124,45 84,811 169,627101,77 7241,52

281,15 ! о! о! о! о 285,08 1 оГ6Т67 о 290,28 jO[O^o7 О 296,42 [0£0£б_£ О 30’3,71 ! о! о"! 6! о 315,94 1 о Го"767 о зз"1,з"з 1оГо"767 о 351,16 ! о! о! о! о 375,15 !оГоТо7 О 403,91 ! О ГоТрТ о

p=o,4 I

Q I TR I PK I x I VD I Zat I ЗК I Pr I N k-wail К I D I Z llnvl 3 517,60 £103,52 ]_390,72^ 32,18 £ 64,36 j 38,62 [ 69,01J -55,69J 0 j -175,77 JoJp£O£O£O 535,82 £107,16 j_ 646,91 £ 43,55 £87,10 j 52,26 [ 71,44J -49,46J 0 J -173,77 _[0_[0J_0j_0J_0 568,05 i 113,61! 911,52 i 53,50 j 107,00 j 64,20 i 75,74 j -46,57 j 0 i -178,36 j 0 j 0 j 0 j 0 j 0 614,48 7122,90 Г1191,427 62,82 Г125.651 75,39 F 81,9з1 -46,427 0 7 -188,98 7 o7o7o7o7o 683,71 ! 136,74j 1497,53! 72,06 ! 144,13 ! 86,48 ■ 91,16 ■ -49,92 ! О | -208,54 ■ 0 ■ 0 ■ 0 ■ 0 ■ 0 777,38 7155,48 Г1 841,297 81,58 Г163Д5¹; 97,89 ! 103,65~! -57,05~! 0 7 -237,40 ] p7 Q T Q T Q T Q 899,90 7179,98-~2 236,017 91,66 ["183,32 j 109,99 ■~119,99~j -68,267 ₀7 -277,04 7 q7₀T₀T₀T₀ 1055,33£211,07 £2 696,59£ 102,56 £205,12 j 123,07 [140,711^3,99 J 0 J -328,83 _[ 0_[0£0£0£0 1249,00 i 249,80 i 3 240,19 i 114,51 i 229,01| 137,411166,53 i-104,90 i 0 i -394,67 i 0 i 0 i 0 i 0 i 0 1487,43p97,49(1886,7o7127,71 p55,431 153,26 [198,32"® l,85l o7 -476,93 7 o7p7p7p7o

517,60 ! 103,52 ! 261,32 I 25,28 I 50,56

Zat I ЗК I Pr I N

535,82 1107,16 I 387,44

554,68 7110,94 ^514,48

574,21 j_114,84 j_642,60

32,02 ! 64,04 !

37,96 £75,92 j

43,38 j_86,75 j

30,34 ! 414,08!

594,42 j 118,88 j 771,93 j 48,42 j 96,84 j 615,34 7123,07 Гб02,60 7 53,19 Г106,371 637,00 7127,40 И 034,777 57,73 Г1"15,4б! 659,42 j 131,88 ! 1168,59 j 62,10 ! 124,20! 682,63 7136,53 Г1304,19Т 66,33 Г132,6б!

706,66 ' 141,33 ' 1441,73 ' 70,44 ! 140,88

52,05 [459,36_£

58,11 i 475,53 i

63,82 I 492,271

468,39! 0 !

480,2o! 0 7

493,25] 0 j

522,39 j 0 i 538,331 0 7

69,28 1 509,601-5^,^.

527,54j|572,82!

546,111-591,34! 565, 3з1-610,74!

555,141 О I

N-HtlndiH

588,47 ! 0 ! 0 ! 0 ! 0 !0

604,51 7 0 7 о T о T о T0

621,94 ! 0 J 0 [ 0 [ 0 [0

640,56 _[0_[0£0£0£0 660,30 i 0 i 0 i 0 i 0 i0

681,09 7 0 7 0 7 о T 0 70

702,93 7 0 7 0 T 0 T 0 70

725,80 ! 0 ! 0 ! 0 ! 0 !0

749,72 ! 0 "! О T О T О T0

Таблица 5

Показатели для второй СБЕ

	P=0,2																				P=0,4
t	n	TR	PK		X	VD	Zat		3K	Pr	N		Pr-N-TR"(l+di)	К D		Z Inv			Э	t	n	TR PK	X	VD	Zat	ЗК	Pr	N	Pr-N-TR*(l«di)	К D	Z	Inv		³
	517,60				72,99				12,94	43,12	8,62		-25,54	⁰	⁰	0		0	0			51,76 ■ 267,14			70,56	34,51	2,70	0,54	-57,88	0 j 0	0		0	0
2	562,49	56,25	665,89		107,67	226,11		139,97	14,06	69,54	13,91		-9,61		⁰	0		0	0	2	535,82	53,58 i 393,08	72,51	152,27	94,26	35,72	15,86	3,17	-49,47	0; 0	0		0	0
3	672,60	67,26	982,21	i 144,11		302,63	187,34		16,81		19,09		-1,66	0 i 0 i 0 i				0	0	3	568,05	56,80 i 523,30	89,87 i 188,72 i 116,83				27,21	5,44	-44,13		0	0		0
4	868.9	86,9	1387,2		186,7	392,1	242,7		21,7	123,7	24,7		-1,8	01 0 i 01				0	0	4	614,48	61,45 1 661,22	107,10 1 224,92 1 139,23			40,97	37,34	7,47	-41,40		0	0		0
5	1182,67 ! 118,27		1936,93		239,82	503,61	311,76		29,57	156,96 ! 31,39				0	0	0	0		0	5	683,71	68,37 ! 812,31	124,98	262,45	162,47	45,58	46,20	9,24	-42,35	0! 0	0	0		0
6	1 657,56 ! 165,76		2 707,60		308,30	647,44		400,80	41,44	197,75	39,55		-34,08	0	0	0		0	0	6	777,38	77,74 ! 982,29	144,12	302,65	187,35	51,83	54,14	10,83	-46,86	0! 0	0		0	0
7	2 353,69	235,37	3 803,22		397,79	835,36		517,13	58,84	248,80	49,76		-73,99			0				7	899,90	89,99 ■ 1177,79	165,14	346,79	214,68		61,32	12 26	-55,33	0 ■ 0			0
8	3 352,23	335,22	5 365,21		514,91	1081,32		669,39	83,81	313,04	62,61		-138,43		⁰	0		0	0	8	1 055,33	105,53 I 1406,29 I 188,63		396,11	245,21	70,36	67,88	13,58	-68.11	0; 0	0		0	0
9	4 761,20 i 476,12 i 7 584,88 i 667,58 i 1 401,92 i							867,86	119,03 j 393,61 i 78,72					oi0ioi				0	0	9	1249,00 i 124,90 i 1676,35 i 215,19 i 451,89 i 279,74					83,27	73,90	14,78			0	0		0
10	6 722,75 1 672,28 1 10 718,711 865,27 1 1 817,06 1 1124,84 1 168,07									493,39	98,78		-384,73	0 j 0 j 0				0	0	10	1487,43 1 148,741 1997,92 1 245,46 1 515,46 1 319,09						79,36	15 87	-109,06		0	0		0
								P=0,6													P=0,8
t	Q	TR	PK		^x	VD	Zat		3K	Pr	N		Pr-N-TR'lltdi)	К D		Z Inv			³	t		TR PK	X	VD	Zat	ЗК	Pr	N	Pr-N-TR*(ltdi)	k\|d	^z	Inv		³
	517,60		218,19								0		-114,35	0	0	0	0		0	1		51,76 ! 196,62			56,07	207,04	-209,80	0	-269,85	0! 0	0	0		0
2	535,82	53,58	300,94		59,35	124,63		77,15	80,37	-47,36	0		-109,52	0	0	0		0	0	2	535,82	53,58 ! 257,70	52,83	110,94	68,68	214,33	-210,64	0	-272.8C	0! 0	0		0	0
3	554,68	55,47	384,36		71,30	149,73		92,69	83,20	-41,14	0		-105,48	⁰	⁰	0		0	0	3	554,68	55,47 ■ 319,30	62,04	130,29	80,66			0	-276,52	0 ; 0	0		0	0
4	574 21	57,42	468 53		82,72	173 71	107 53		86 13	-35,46	0		-102 07		0	0		0	0	4		57,42 i 381,50	70 90	148,90	92 17			0	-280 91	0 i 0	0		0	_Lo
5	595,05	59,50	553,65		93,75	196,87	121,87		89,26	-30,32	0		-99,35	oi 0 i 0			0		0	5	594,42	59,44 i 444,36	79,50	166,94 i 103,34 i 237,77			-216,97	0	-285,92		0		0	0
6	623,94	62,39	641,03		104,64		136,03		93,59	-26,72	0		-99,10	0	010		0		0	6	615 34	61,53 i 507,94	87,88	184,55 i 114,25 i 246,14			-220.13	0	-291,51		0		0	0
7	657,99	65,80	731,46		115 53	242,61	150,19		98,70	-24,04		0	-100,37	0! 0 ! 0				0	0	7	637,00	63,70 1 572,33	96,11 1 201,84 1 124,95 1 254,80				-223,77	0	-297,67		0		0	0
8	699,51	69,95	826,11		126 57	265,79	164,54		104,93		0		-103,70	0	0	0	0		0	8	659,42	65,94 j 637,59	104,22 ! 218,86 ■ 135,48 ■ 263,77				-227,87	0	-304,37	0! 0	0	0		0
9	748,15	74,82	926.02		137,88	289,55	179,25		112,22	-22.12	0		-108,90	0	0	0		0	0	9	682,63	68,26 ! 703,79	112,23	235,69	145,90	273,05	-232,42	0	-311,60	0! 0	0		0	0
10		ЯЛ ^1	1 П37 4'		1ZLQ ЯЛ	Я121 1Я		194,48	17Л 7Я	-7? Я1	Q		-11Я 70	"0	0"	0		Q		1 n	706,66	70,67 I 771,01	1 ?Л 1Я	252 38	1 яя ?д	7Я? 67	-?Я7 4Л	Q	_31 q ^7	л ! n	0			л

Таблица 6

Показатели для третьей СБЕ

	P=0,2																			P=0,4
t	⁰	TR	PK	X	VD	Zat	3K	Pr	N	Pr-NTR*(l»di)		К		^D			Inv	Э	t	°	TR	PK		X	VD	Zat	3K	Pr	N	Pr-N-TR^Hdi]	К	^D		Z	Inv	Э
1			398,48		211,98	127,19		69,52			-4,42		0				0		1		51,76 :		269,08	70,38 ■ 154,83		92,90		21,22		■43,07		0
2	562,49	56,25	667,77	145,63	320,38	192,23	14,06	111,56	22,31		24,00		24,00	4,80		,60	9,60	0,43	2	535,82	53,58 ;		394,96	95,67 j 210,48 j 126,29			35,72	42,04	8,41	■28,52	0	0		0
3	672,60	67,26	1032,03	206,30	453,86	272,31	19,21	158,87	31,77		49,07	49,07		9,81 i 19,63 i 19,63 io,73					3	568,05	56,80			120,16 i 264,35 i 158,61				61,05	12,21		о	0				0
4	Я6Я.9	Я6.Ч	1 533 7	283.2	623 1	373 9	26.6	217.8	43 6		73 5	73 4.5		14,691 29,38129,3810,85					4	614,48	61 4.5	662,99		144,79 1 318,541 191,13			40,97	79.08	15.82		о	0		0	0	0
5	1182,67! 118,27		2 225,92	381 55	839,40	503 64	36 91	292 20	58 44		96 57	96 57		19,31! 38,63			38,63! 0,82		5	683 71	68 37	814,03		170,63 ! 375,38! 225,23			45 58	96 37	19 27	-2,22 ! 0		0		0	0	0
	1657,56! 165,76		3 181,06	507,69	1116 92	670,15	51,10	386 47	77,29		116,90	116,90		23,38* 46,76			46,76! 0,71		6	777,38	77,74 I		983.95	198,57 ! 436,86! 262,12			51,83	113 59	22 72	0 70	0,70	0,14		0,28	0.28	0 01
	2 353,69	235,37	4496,29	669,61	1 473,15	883,89	70,53	506,03	101,21		131,80	131,80		26,36	52,72		52,72	0,56	7	899,90	89,99 :		180,11	229,66 i 505,24		303,15	60 IS	131,09	26,22	0,48	0,48	0,10		0,19	0,19	0,01
8	3 352,23 i 335,22		6 301,10	877,15	1 929,73	1157,84	96,99	657,45	131,49 ;		137,10	137,10		27,42\| 54,84			54,84 j 0,41		8	1055,33,105,53 i 1409,02				264,65 j 582,23 ; 349,34			70,48	149,72	29,94	-2,64	0	0		C	0	0
9	4 761,20 i 476,12 i 3 766,87 i 1142,40 i 2 513,27 i 1507,96 i 132,74							848 67	169,73 j		126,64	126,64 \| 25,33 i 50,66 i 50,66 i 0,27							9	1249,00 i 124,90 i 1678,99 i 304,50 \| 669,89 i 401,93								169,70	33,94		o	0		0	0	0
10	6 722,751672.28112 118,521 1480,131 3 256,291 1953,781 180,73							1O№	217 85		91 56	91 56		18,31 j 36,62 1 36,62 1 0,14					10	1487,43 I 148,74 1 2 000,48 i 350,311 770,67 1 462,40								191 26	38.25		о	0		0	0	0
							P=0,6
t	⁰	TR	PK	^x	VD	Zat	3K	Pr	N	Pr-N-TR*(1«II)		X		^D	^z		Inv	³	t	ⁿ	TR	PK		X	VD	Zat	3K	Pr	N	Pr-N-TR'U+di]	к	^D		z	Inv	³
1			218,19		130,93	78,56		•39.24	0	-99,29		0		0	0		0	0	1			196,62			120,47		207,04	-196,12! 0		-256,16 ! 0		0		0	0	0
2	535,82	53,58	300,94	76,97	169,34	101,60	80,37	-27,11	0		-89,26		0	0			0	0	2	535,82	53,58 I		257,70	67,99 1149,57		89,74	214,33		0	-255.23	Q	0	। 0		0	Q
3	554,68	55,47	384,36	93,61	205,95	123,57	83,20	-15,80	0		-80,14		0	0			II	0	3	554,68	55,47 :		319,30	80,71 ; 177,55		106,53	221,87		0	-255.13		0			0
4	574,21	57,42	468,53	109,68	241,30		86,13	-5 11	0		-71 72		0	0		0	0	0	4	574,21 i 57,42 i 381,50 j 93,05 \| 204,72 \| 122,83 i 229,68								-18914 0		-255 74	0	0		0	Q	0
5	595,05		553,65	125,35	275,77	165,46	89,26	4 99		-65,04		0		0	0		0			594,42	59,44		444,36	105,13 I 231,291 138,77 i 237,77					0	-257,00	0	0			Q	0
6	623,94	62 39	641,03	140,94	310,08	186,05	93 59	13 59	3		-61 50		0	0			0	0	6	615 34	61 53	507,94		117,00 1 257,401 154,44 1 246,14					0	-258,86	0	0	i 0		0	0
	657 99	55 80	731,46	156,64	344,60	206,76	98,70	21 38	4		-59 22		Q	0		0	0	0	7	637,00	63 70			128,72 ! 283,19! 169,92 ! 254,80				-187 39	0	-261 28	0	0	J P		0	0
g	699,51	69 95	826,11	172 65	379 83	227,90 ! 104,93		28 12	6	-58 65		0		0	0		0	0	8	659 42	65 94			140,34 ! 308,74! 185,25 j 263,77					0	-264 24	0	0		0	0	0
g	748 15	74 82	926 02	189 16	416 16	249 69	112 22	34 04	7		-59 55		0	0		Q	0	0	9	682 63	68 26	703 79		151 88	334 13	200,48	273 05		0	-267 74	Q	0		c	0	Q
10	805,05	80,51	1032,41	206,36	453,99	272,39	120.76	39,10	8		-62,11		0	0			0	0	10	706,66	70.67 :		771.01	163,38 I 359,43		215,66	282.67		0	-271.75		0		0	0

Таблица 7

Показатели для четвертой СБЕ

p=0,2

PK x

Zat | 3K

Pr-H-TR-jlHil К

Z 1 Inv

PK 1 x

VD | Zat | 3K

Pr-N-1«’(lAiil К 0

Z | Inv | Э

517,60 ; 51,76 ; 400,42 ; 114,82 ; 252,60 ; 151,56 ; 12,94

17,15 ; 8,58 ; 8,58 ; 1,72 ; 3,43 ; 3,43 ; 0,17

51,76 ; 271,02 ; 83,05

182,70 ; 109,62 ; 34,51

32 36

6,47 ; -34,15 ; 0 ; 0 ; 0 ; 0 ; 0

562,49 I 56,25 i 686,80 i 179,68 i 395,29 i 237,17 j 14,92

140,51

28,10 : 47,16 : 47,16 : 9,43 : 1&86 : 18,86 : o,84

535,82

53,58 I 396,84 j 113,97

250,73 j 150,44 ; 35,72

58,14

11,63; -15,64 : o : o : o : o : o

672,60

67,26

1096,82 i 264,99

582,98

349.79 i 21,53

207 79

41 5Б

88,21 i 88,21

17,64

35,28 i 35,28

1,31

563,05

5Б SCI

526,95 i 144,21

317.26 i 190,36 i 37,87

82,22

16,44 I -0,12 i 0 i 0

0 i 0 i 0

RAS 9

SA 9

1674,8 1 376,5

R7R 4

497,0 1 30,5

295 з

59 1

135,5 1 135,45

77 09

54,18 1 54,18

1 SA

614,48

Al 4S

664,76 1 174,88

384,73 1 230,84 1 40.97

105 SA

71 11

13,16 1 13,16 l 2.63

5,27 1 5,27 1 0,21

1182,67

118 27

2486,80 ! 522,76

1150,08

690,05 ! 43,11

409,16

81,83

190,14 I 190,14

38,03

76,06 ! 76,06

1,61

683,71

68,37

828,91 ! 210,03

462,07 I 277,24 ! 49,09

126,90

25 38

22,21 ! 22,21 ! 4,44

8,88 ! 8,88 ! 0,32

1657,56 ! 165,76! 3 621,24 ! 714,13 I 1571,08 I 942,65 I 60,45

557,10

111,42 ! 253,40 ! 253,40 I 50,68 ! 101,36 I 101,36 I 1,53

777,38

77,74 ! 1020,60 ! 249,62

549,16 ! 329,49 I 57,75

151,52

30,30 I 31,04 ! 31,04 ! 6,21 ! 12,42 ! 12,42 ! 0.40

2 353,69 ; 235.37 ■ 5196,26 ■ 963,71 ■ 2120,16 ■ 1272,10 ■ 84,18

748,73

149,75 ; 325,96 ■ 325,96 ■ 65,19 ■ 130,38 ■ 130,38 ■ 1,38

899,90

89,99 ; 1246.00 ■ 294,58

648,07 ; 388,84 ■ 68.27

178,67

35,73 ■ 38,55 ; 38.55 ■ 7,71 ■ 15,42 ■ 15,42 ■ 0,43

3 352,23 j 335,22 1 7 368,40 1 1287,78 1 2 833,13 j 1699,88 1 116,40

995,90

199,18 j 407,86 j 407,86 1 81,57 1 163,14 1 163,14 1 1,22

1055 33

105,53 j 1511,00 j 345,71

760,56 j 456,34 j 80,63

209 08

41,82 j 44,84 j 44,84 1 8,97 j 17,94 1 17,94 1 0,42

4 761,20

476,12

10 343,66 i 1 706,49

3 754,27

2 252,56 i 159,82

1313,13

-Г71Я16-

262,63

498,20 i 498.20

99,64

199,28 i 199,28

1,05

1 249,00

124,90

1822,76 i 403,95

888.69 i 533,22 i 95,22

243,11

48,62

49,61 i 49,61 i 9,92

19,84 i 19,84 i 0,40

A 777 7S

A77 7R

14 391,13 1 2 244,62

4 938,16

2 962,90 । 217,89

SdA AS

594,68 1 594,68

118,94

237,87 1 237,87

A SR

1487,43

14R 74

2 189,54 1 470,34

1034,76 । 620,85 1 112,39

7R1 7R

56,26 1 52,49 1 52,49 । 10,50

20,99 1 20,99 1 0,35

P-0,6

PK | x

Zat | 3K

Рг*'П|ф«Л)| К

Z 1 Inv

PK 1 x

VD | Zat | 3K

Pr-N-T6-(l««l| К | D

Z 1 Inv I Э

517 60

51 76

218,19 ! 69,37

152 61

91 56 ¹ 77 64

-30 57 ¹ 0

-90,61 I 0

0 ¹ 0

•

517 60

51 76

196,62 ! 63,63

139,98 ! 83,99 | 207,04

-248,36 ! 0 ! 0

о ! о ! о

535,82 I 53,58 I 300,94 I 90,59 I 199,29 I 119.58 I 80,37

-15,12 I 0 I -77,28 ! 0 ! 0 ! 0 ! 0 ! 0

535,82

53,58 I 257,70 I 79,64

175.21 I 105,13 I 214,33

0 ! -244,98 ! 0 ! 0 ! 0 ! 0 ! 0

554,68 ' 55,47 ■ 384,36 ' 110,98 ' 244,16 ' 146,50 ' 83,20

-0,51 • 0 ' -64,86 ' 0 ' 0 ' 0 ' 0 ' 0

554 68

55,47 ' 319,30 ' 95,15

209,33 ; 125,60 ; 221,87

-170,40

0 • -242,42 ' 0 ' 0 ' 0 ' 0 ' 0

574,21

57,42

468,53 i 130,81

287,78

172,67 i 86,13

13,48 i 2,70

-55,83 0

0 1 0

594,42

59 44

Ь-Звк^-кУкк

444,36 i 125,18

242.65_i 2k-?2 j_².29,68

275,40 i 165,24 i 237.Л

./²^?L.Lk_Lk._

-239,36 i 0 i 0

6 i 0 i 6

S9S 05

59,50

553,65 i 150,25

330,55

198,33 i 89,26

26,89 i 5,38

-47,51 i 0

0 | 0

623,94

62,39

641,03 i 169,68

373,30

223,98 i 93,59

38,88 i 7,78

-41,27 i 0

0 1 0

615,34

61,53

507,94 i 139,88

307.73 1 184,64 1 246,14

-238,73 i 0 i 0

0 i 0 i 0

AS7 QQ

AS ЯЛ

731,46 1 189,32

41A SI

249,91 1 98,70

50,14 1 10,03

-36,21 1 0

n 1 <1

637,00

AS 7П

572,33 । 154,44

339,78 1 203,87 1 254,80

-238,65 1 0 1 0

0 । 0 1 0

699 51

69.95

826,11 ! 209,44

460 77

276.46 ! 104,93

60,49 I 12,10

-32 75 ¹ 0

0 * 0

659 42

65.94

637,59 ! 168,92

371,63 ! 222,98 ! 263.77

-239,09 ! 0 ! 0

о ! о ! о

748 15

74 82

926,02 I 230,26

506 57

303,94 I 112,22

70,20 I 14,04

-30 62 ' 0

0 ' 0

682 63

68 26

703,79 I 183,36

403,39 I 242,03 I 273,05

-240,03 ! 0 ! 0

0'0'0

805,05 ! 80,51 ! 1032,41 I 252,01 I 554,43 I 332,66 I 120,76

79,28 1 15,86 ! -29,97 I 0 I 0 I 0 I 0 I 0

706,66

70,67 I 771,01 ! 197,78

435.12 ! 261,07 I 282,67

0 I -241,47 I 0 ! 0 ! 0 ! 0 ! 0

Таблица 8

Показатели для пятой СБЕ

								6=0,2									9=0,4
t	Q	TR	PK	X	VD	Zat	3K	Pr	N	PHHR-flRin	к	D	2	Inv	э	t	n		TR	PK	X	VD	Zat	3K	Pr	N	рмм«^>«к)	к	D	z	Inv	3
	517,60	51.76	402,36	169,73	390,38	227,44		147,67		58,10	58,10	11,62	23,24	23,24	1,12	8		517,60	51,76	272,96	119,70	275,31	160,40	34,51	74,19	14,84	-0,69	0	0	0	0	0
	562,49	56.25	787,72	310,70	714,61	416,34	19,87	274,82	54,96	154,61	154,61	30,92	61.84	61,84	2.75			535,82	53,58	398,73	168,35	387,20	225,59	35,72	119,46	23,89	33.42	33.42	6.68	13,37	13.37	0,62
	672,60	67.26	1409,61	524,56	1 206,49	702,91	32,28	465,49	93,10	294,37	294,37	58,87	117.75	117.75	4,38			568,05	56,80	562,19	229,35	527,51	307,33	46,78	164,98	33,00	66,09	66.09	13,22	26,44	26.44	1,16
	868.9	86,9	2 390,5	843,8	1940.8	1130,7	51,2	749,7	149,9	499,0	498,96	99,79	199,59	199.59	5.74			614,48	61,45	765,03	302,63	696,06	405,53	58,59	221,39	44,28	105.84	105,84	21,17	42,33	42.33	1.72
	1182,67	118,27	3 908,08	1313,33	3020,65	1759.86	79,46	1167,03	233,41	796,43	796,43	159.29	318,57	318.57	6.73			683,71	68,37	1018,85	391,65	900,81	524,82	73,80	288,90	57,78	151,81	151,81	30,36	60,72	60.72	2.22
	1657,56	165,76	6212.48	1993,17	4584,29	2 670,85	121,08	1770,57	354,11	1224,18	1224.18	244.84	489,67	489.67	7.39			777,38	77,74	1334,44	499,31	1148,42	669,08	92,31	370,42	74,08	206,16	206,16	41,23	82,46	82.46	2.65
	2353,69	235,37	9651.31	2 963,01	6814,93	3 970,44	181,26	2 630,60	526,12	1831,45	1831.45	366.29	732,58	732.58	7.78			899,90	89,99	1725,54	629,27	1447,32	843,22	114.97	468,44	93,69	270,36	270,36	54,07	108.14	108,14	3,00
	3 352,23	335,22	14 700,79	4 327,25	9952,68	5 798.52		3 839,16		2 682,47	2 682.47	536.49	1 072,99	1072.99	8.00			1 055,33	105,53	2 207,97	785,59	1806,87	1052,70	142.45	586,08	117,22	346,44	346,44	69,29	138.58	138,58	3.28
	4 761,20	476,12	22 005,31	6 221,29	14308,97	8336.53		5515^45	1103,09	3 860,06	3 860,06	772.01	1 544,02	1544,02	8,11			1249,00	124,90	2 800,42	972,99	2 237,87	1303,80	175.65	726,80	145,36	436,55	436,55	87,31	174.62	174,62	3.50
	6 722,75 1 672,28 i 32 426,65 i 8 818,96 i 20 283,62 i 11817,41 i 554,08							5515^45	1562,48 i 5 470,08 i 5 470,08 i 1094,02 i 2 188,03 i 2188,03 i 8,14									1487,43 i 148,74 i 3 524,82 i 1196,82 i 2 752,68 i 1603,74 1 215,58							894,57	178,91 i 543,11 i S43.ll i 108,62 i 217,24 1 217,24 i 3,65
								p=o,6																	0.3
	n	TR	PK	X	VD	Zat	3K	Pr	N	Pr-N-lR*ri»4i1	К	D	z	Inv	э	t			TR	PK	X	VD	Zat	3K	p.	N	Pr-N-TR*(lt4i)	к	D	z	Inv	э
8	ы / ъи	51 /О	218 19	97 85	225 05	13112	77 64	2 32	0 46	-58 19		0		0		8
	535 82	53 58	300,94	130 69	300 59	175 12	80 37	30 62	6 12	-37 66	0	0	0	0	о			535 82	53 58	257 70	113 66	26142	152 30	214 33	^43,79		-205 95	о	0	о	0	о
	554 68	55 47	384 36	162 88	374 63	218 26	83 20	58 19	11 64	-17 79	0	0	0	0	0			554 68	55 47	319 30	137 84	317 04	184 71	221 87	^43,79	0	-193 82	о	0	0	0	n
	574 21	57 42	468 53	194 66	447 71	260 84	86 13	85 24	17 05	1 58	1 58	0 32	0 63	0 63	0 03			574 21	57 42	38150	161 ?9	372 12	216 80	229 68		0	-182 31	0	0	0	0	0
	595 05	59 50	554 71	226 60	52118	303 65	90 21	111 09	22 22	19 85	19 85	3 97	7 94	7 94	0 33			594 42	59 44	444 36	185 59	426 87	248 70	237 77		0	-171 35	0	0	о	0	о
	673 44	67 39	HAS 79	763 77	605 51	357 7R	105 sn	17R 75	75 65	30 77	30 77	6 04	17 09	17 09	0 4R			615 34	61 53	507 94	709 33	4R1 47	7ЯП 51	746 14			-160 KA	о	о	о	о	о
	657 99	65 RO	765 44	307 7R	696 39	405 72	HR RR	1S7 Я1	30 56	45 97	45 97	9 1R	1R 37	1Я 37	0 70			637 OO	63 70	572 33	733 07	536 06	317 31	754 RO	76 97		150 RI	о	0	о	о	□
	699 51	69 95	889,68	346 67	797 34	464 54	137 4Я	176 4Я	35 30	60 04	60 04	17 01	74 01	74 01	0 Я6			659 47	65 94	637 59	756 Я6	590 77	344 19	763 77	64 66	0	141 16	о	0	о	о	о
	7dR 15	74 Я?	1 077 7П	394 77	AO7 RS	А7Я 97	1ДЯ 75	704 00	40 RO	76 41	76 41	15 7Я	SO 57	SO 57	1 07			6Я7 63	6Я 76	70S 79	7ЯП 74	645 70	376 19	773 П5	.57 69	0	-131 ЯЯ		о	о		о
	805,05 ' 80,51 ' 1181,99 ' 447,67 I 1029,64 ' 599,88 ' 166,61							233,17	46,63 ' 93,15 ! 93,15 ' 18,63 ' 37,26 ' 37,26 ' 1,16									706,66 ' 70,67 ! 771.01 ' 304,76 ' 700.95 ' 408,38 ' 282,67							-40,97	0 I -122,95 ! 0 ! 0 ' 0 ' 0 ' 0

Таблица 9

Динамика эффективности вложенных средств и объема средств централизованного инвестиционного фонда ИГП

Выводы

Сделаем выводы, согласующиеся с выводами работ [6, 8, 22], относительно динамика денежных потоков ИГП:

1. С увеличением степени однородности производственной функции эффективность рабочего капитала СБЕ растет адекватно росту трансфертов от УК.
2. Эндогенные факторы выбраны корректно: выполняется условие пропорционального роста заемного капитала и рентабельности, а также эффективности рабочего капитала с ростом риска его структуры.
3. Существенное значение имеет фактор налогового щита: увеличение финансового рычага ведет к росту объемов промежуточного и конечного продуктов.

	В,=0.2			В,=0.4
	I : 2 : 3 : 4 : s : 6 : 7 : s : 9 : 10			1:2:з:4:5:б:7: 8 : 9 : ю
э_лЭ,	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 ■ 0 ■ 0 ■ 0 ■ o' o' o' o' o' 0		3i 3₂	о:о:о:о:о:о:о: о о'о'о'о'о'о'о' 0	о : о 0 ' 0
э₃	0 ! 0,43 ! 0,73 ' 0,85 ' 0,82 ' 0,71 ' 0,56 ' 0,41 ' 0,27 ' 0,14		Эз	о'о'о'о'о'о'о! о	0 I 0
Эл Эз	_0,17 j 0,84 j 131 j 136 j 1,61_!_1,53 \| 138 _ 1,12 Г 2,75 T 4,38 7 5,74 7 6,73 Г 7,39 Г 7,78	_1,22_ !_1,05 I 0,88_ 8,00 I 8,11 7 8,14	э₄ " 3₅	_ о_ ! о ! 0 ! 031 ! 032 I 0,40_! 0,43_! _0,42 0 Г 0,62 Т 1,16 7 1.72 7 2,22 1 2,65 [ 3,00 I 3,28	_ 0,40 I 0,35_ 3,50 7 3,65
э₆	0,21 i 0,67 i 1,07 i 1,36 i 1,53 i 1,60 i 1,62	1,60 i 1,57 i 1,53	3₆	0 i 0,10 i 0,19 i 0,32 i 0,42 i 0,51 i 0,57 i 0,62	0,65 i 0,67
QI 517,60 j 562,49 j 672,60 868,93 1182,67 1657,56 2353,69 3352,23 4761,20 6722,75			n	517,60 j 535,82 568,05 614,48 683,71 777,38 899,90 1055,33	1249,00 j 1487,43
	Вз=0,6			₽₄=0,8
	i i 2 i з i 4 i si 6 i 7	8 i 9 i 10		1\|2\|3\|4\|5\|6\|7\| 8	9 i 10
A 3₂	0 i 0 i 0 i 0 i 0 i 0 i 0 о ; о ; о ; о ; о ; о ; о	0 i 0 i 0 0'0'0	Э1 3₂	о;о;о;о;о;о;о; о o;o;o;o;o;o;o; о	0 0
Эз	о : о : о : о : о : о : о	о : о : о	Эз	o!o:o:o:o:o!o: о	0 : 0
э₄	о : о : о : о : о : о : о	о : о : о	э₄	o:o:o:o:o:o:o: о	о : о
Э₅	0 0 0 I 0,03 I 0,33 0,48 0,70	0,86 ! 1,02 ! 1,16	э₅	ololololololo! о	0 1 0
э₆	о ! о ! о ! о,оо ! о,об ! o,os ! 0,12	0,14 ! 0,17 ! 0,19	э₆	o!o!o!o!o!o!o! о	0 ! 0
n	517,60 ! 535,82 ! 554,68 ! 574,21! 595,05 ! 623,94 ! 657,99	699,51 ! 748,15 ! 805,05	n	517,60 ! 535,82 ! 554,68 ! 574,21! 594,42 ! 615,34 ! 637,00 ! 659,42	682,63 ! 706,66

Список литературы Моделирование внутрифирменных денежных потоков интегрированной группы предприятий

Алчян А.А., Демсец Х. Производство, стоимость информации и экономическая организация // Вехи экономической мысли. Т. 5. Теория отраслевых рынков. СПБ., 2003. 344с.
Анохина П.Н., Беляева Д.И., Димитриев А.М., Максимов Д.А. Оптимизация внутрифирменного кредитования подразделений иерархической производственной структуры с критериями игры с природой // Вестник Алтайской академии экономики и права. 2020. № 1-1. С. 4-16.
Ансофф И. Новая корпоративная стратегия. СПб.: Питер, 1991. 630 с.
Антиколь А.М., Халиков М.А. Нелинейные модели микроэкономики: учеб. пособие. М.: ФГБОУ ВПО "РЭУ им. Г.В. Плеханова", 2011. 156 с.
Аоки М. Введение в методы оптимизации. Основы и приложения нелинейного программирования. М.: Наука, 1977. 343 с.
Бабаян Э.А., Расулов Р.М., Халиков М.А. Динамические модели "затраты-выпуск" // Экономика природопользования. 2013. № 2. С. 3-16.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М., Численные методы. М.: Бином, Лаборатория знаний. 2003. 632 с.
Безухов Д.А., Халиков М.А. Математические модели и практические расчеты оптимальной структуры производственного капитала предприятия с неоклассической производственной функцией// Фундаментальные исследования 2014. № 11-1. С. 114-123.
Безухов Д.А., Халиков М.А. Выбор оптимального варианта обновления основного капитала предприятия с учетом рисков производственной сферы // Фундаментальные исследования. 2015. № 4. С. 191-198.
Владимирова И.Г. Организационные формы интеграции компаний // Менеджмент в Росси и за рубежом. 1999. № 6. С. 113-129.
Горский М.А. Теоретический подход и численный метод поиска квазиоптимального решения нелинейной дискретной задачи большой размерности // Экономический журнал Высшей школы экономики. 2019. Т.23. № 3. С. 465-482.
Иванова В.О. Особенности менеджмента вертикально-интегрированной компании // Российское предпринимательство. 2011. Т. 12. № 11. С. 55-60.
Классификация и структура холдингов в современных условиях / Портал Юристъ [Электронный ресурс]. Ресурс доступа: https://lawbook.online/hozyaystvennoe-pravo-rossii-kniga/klassifikatsiya-struktura-holdingov-23558.html (дата обращения: 23.11.2019).
Клейнер Г.Б. Производственные функции: теория, методы, применение. М.: Финансы и статистика, 1986. 239 c.
Клейнер Г.Б. Предприятие в нестабильной экономической среде: риски, стратегия, безопасность / Г.Б. Клейнер, В.Л. Тамбовцев, Р.М. Качалов. Под общ. Ред. С.А. Панова. М.: Экономика, 1997. 286 с.
Клейнер Г.Б. Стратегия предприятия. М.: Дело, 2008. 436 с.
Колемаев В. А. Математические методы и модели исследования операций. М.: ЮНИТИ-ДАНА, 2012. 592 с.
Логоша Б.А., Дегтярева Г.Г., Шаркович В.Г., Методы и модели совершенствования организационных структур. М.: Наука, 1998. 189 с.
Максимов Д.А., Халиков М.А. Методы оценки и стратегии обеспечения экономической безопасности предприятия. М.: ЗАО " Гриф и К °", 2012. 220 с.
Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. М.: Наука, 1978. 351 с.
Расулов Р.М. Динамическое моделирование "затраты-выпуск" на основе однородных разностных уравнений второго порядка // Системный анализ в экономике - 2012. Секция 2 / Материалы Научно-практической конференции. Москва, 27-28 ноября 2012 г. М.: ЦЭМИ РАН, 2012. С. 151-156.
Расулов Р.М., Халиков М.А. Факторы динамики "Затраты-выпуск": проблематика оценки и учета в моделях предприятия // Вестник Российского экономического университета им. Г.В. Плеханова 2013. № 4(58). С. 70-80.
Халиков М.А. Дискретная оптимизация планов повышения надежности функционирования экономических систем // Финансовая математика. Сб. ст. М.: МГУ, 2001. С. 281-295.
Халиков М.А., Максимов Д.А. Об одном подходе к анализу и оценке ресурсного потенциала предприятия // Международный журнал прикладных и фундаментальных исследований. 2015. № 11-2. С. 296-300.
Халиков М.А. Моделирование производственной и инвестиционной стратегий машиностроительного предприятия. М.: Изд-во "Благовест-В", 2003. 304 с.
Халиков М.А. Методы анализа и оценки риска рыночной деятельности подразделений иерархической производственной структуры // Менеджмент в России и за рубежом. 2009. № 1. С. 108-120.
Халиков М.А., Максимов Д.А. Концепция и теоретические основы управления производственной сферой предприятия в условиях неопределенности и риска // Международный журнал прикладных и фундаментальных исследований. 2015. № 10-4. С. 711-719.
Халиков М.А., Хечумова Э.А., Щепилов М.В. Модели и методы выбора и оценки эффективности рыночной и внутрифирменной стратегий предприятия. М.: Коммерческие технологии. 2015. 595 с.
Халиков М.А., Никифорова М.А., Модели оценки критического объема производства многономенклатурного предприятия с учетом рыночного риска // Фундаментальные исследования. 2017. № 11. С. 248-252.
Юдин Д.Б., Горяшко А.П., Немировский А.С. Математические методы оптимизации устройств и алгоритмов АСУ / Под ред. Ю.В. Асафьева, В.А. Шабалина. М.: Радио и связь, 1982. 288 с.
Якутин Ю.В., Корпоративные структуры: вариант типологизации и принципы анализа эффективности // Российский экономический журнал. 1998. № 4. С. 28-35.
Luenberger D., Yinyu Y. Linear and Nonlinear Programming. Springer Science + Business Media, LLC, 2008. 551 p.
Maximov D.A., Khalikov M.A. Prospects of institutional approach to production corporation assets assessment // Actual Problems of Economics. 2016. V. 183. № 9. P. 16-25.
Minniti A., Turino F. Multi-product firms and business cycle dynamics. European Economic Review. 2013. V. 57. P. 75-97.

Еще

Статья научная