Моделирование волновых процессов в механике структурно ориентированных взаимодействий твердых тел

Самарский государственный технический университет

В работе рассмотрена модель волновых функций беговых дорожек бурового горнорудного долота, с помощью которой получены оптимальные начальные значения кольцевых и диаметральных зазоров структурно упорядоченной сборки, при которых расчетный ресурс изделия увеличивается в несколько раз.

Кинематика взаимодействия роликов в опорах качения предполагает циклические процессы, физические закономерности которых целесообразно исследовать с использованием волновых функций. Конструкция опор бессепараторного типа может быть представлена системой обыкновенных дифференциальных уравнений, поскольку независимые переменные интенсивностей изменений кольцевых Х1(t) и диаметральных Х2(t) зазоров не входят явно в динамическую составляющую системы. Количество независимых переменных определяет автономную систему взаимодействия роликов второго порядка с двумя степенями свободы

Рис. 1. Роликовая опора бурового горнорудного долота dX = A( X,'X 2)

X = f , ( X , , X 2 ) '

I dt

где f ₁ и f ₂ – волновые функции взаимодействия роликов в опорах качения; X ₁ , X ₂ , t – соответственно параметры кольцевых, диаметральных зазоров и время предельного состояния механической системы.

В процессе эксплуатации изделия в опоре создается механическая волна, которая является следствием кинематики циклических взаимодействий роликов по большой и малой роликовым дорожкам, при этом их траектории последовательно проходят две анизотропные зоны в секторах опоры (рис. 1).

Первый сектор характеризуется натягом в сопровождении роликов с дорожками качения со стороны действия внешней силы Р. Второй сектор расположен с диаметрально противоположной стороны и характеризуется зазором. По мере продвижения роликов по дорожкам качения они претерпевают различные процессы, которые в параметрическом виде можно задать изменениями кольцевых и диаметральных зазоров.

Чтобы процесс качения роликов мог продолжаться по беговым дорожкам, необходимо гарантированное значение зазоров в двух секторах опор. Отсутствие гарантированного зазора приведет к заклиниванию роликов и как следствие нарушению работы долота (рис. 2).

Метод синтеза в рамках указанных условий взаимодействия роликов позволяет разработать модель волновой функции состоящей из

Рис. 2. Заклиненная опора бурового горнорудного долота двух уравнений интенсивности изменения зазоров, зависящих как от углов взаимодействия между роликами и углов секторов опор, так и от взаимного влияния зазоров между собой. Используя принцип различимой конструктивной симметрии роликов, в конструкцию введена структура их размерной последовательности [1]. Эту особенность сборки опор в модели волновой функции представляет параметр размерной упорядоченности роликов в виде отношения разностей их действительных значений диаметров[d(n)-d(n-1)]/[d(n-1)-d(n-2)] повторяемых циклов размерной последовательности, состоящей из n+1 селективных групп роликов. Процесс взаимодействия роликов можно записать в виде волновой функции.

Волновая функция для большой роликовой дорожки имеет вид:

"             [ ( D + d ) - d ] f    p_x

(2 - n - R — ¹⁶ D ) •      D 2-K • J • xi

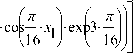
f(t , X) =

( R2 — R — D 3) • tan-

P2     • L n )

Arx^ • siii7—x^ I- exp7— I 2Б J 2  V 16 2 J X

(D— D) L Ppi    fn  )

--1 AiБ---xi • coS— • xi !• exp3^ — D — d I 1  J  1   Vi6 1JX

(2) волновая функция для малой роликовой дорожки имеет вид:

ft x) =

(2 ^ n ^ r 1 — 11 ^ 1 ) ^

[ ^{( d} 1 ⁺ d 2 ) - d ] d ₃

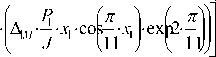
(r₂ — Г 1 - d 3 ) ^ tan

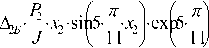
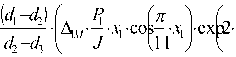
где R ₁ , R ₂ , r ₁ , r ₂ – действительные размеры радиусов больших и малых беговых дорожек соответственно охватывающей и охватываемой детали роликовой опоры, мм; D ₁, D ₂, D ₃, d ₁, d ₂, d ₃ – действительные размеры диаметров больших и малых роликов структурно упорядоченной последовательности, взятой из соответствующих селективных групп, мм; A 1 Б , A 2 б , A 1 м , A 2 м - параметры анизотропии взаимодействия больших и малых роликов в секторах соответственно с натягом и зазором; P ₁, P ₂ – значения импульсов сил взаимодействия от внешней нагрузки на роликовую опору, Н; J – жесткость роликовой опоры, Н/мм [2]; X ₁, X ₂, x ₁, x ₂ - соответственно кольцевой и диаметральный зазоры на большой и малой роликовой дорожке опоры, мм.

Решение находим в параметрическим виде интегральных кривых и фазовых траекторий автономной системы, используя программу Mathcad. Для нахождения решения (2) задаемся начальными условиями параметров для двух вариантов значений кольцевых и диаметральных зазоров, взятых из конструкторской документации на данный тип бурового долота (табл. 1).

Значения переменных и констант для роликовой опоры типа ГВ представим для большой роликовой дорожки в табл. 2, для малой роликовой дорожки в табл. 3. Численные данные соответствуют конструкторской документации на буровое долото 215,9 СЗ-ГВ.

По характеру фазовых траекторий системы (рис. 3, 4) оценим результат эффективности процесса структурно упорядоченной сборки роликовых опор.

Это условие предельных состояний работоспособности проверяется на моделях волновых функций (2) и (3) методом случайного поиска начальных значений кольцевых и диаметральных зазоров структурно упорядоченной сборки опор качения [3].

В результате мы получаем из двух вариантов значений кольцевых и диаметральных зазоров четыре варианты сборки роликовой опоры бурового долота.

На рис. 5 – 7 представлены фазовые траектории для четырех вариантов сборки роликовой опоры в целом.

Для анализа полученных результатов

Таблица 1. Данные для расчета

Параметры	Значения зазоров на этапе сборки, мм
	Первый вариант	Второй вариант
X 1	2,13	1,98
X 2	0,06	0,28
х 1	1,92	1,8
х 2	0,04	0,28

Таблица 2. Значения переменных и констант для роликовой опоры типа ГВ для большой роликовой дорожки

R 1	R 2	Δ 1Б	Δ 2Б	D 1	D 2	D 3	P 1	P 2	J
мм	мм	-	-	мм	мм	мм	Н	Н	Н/мм
32,175	38,44	1,0075	0,9924	12,5	12,494	12,487	1,3Ч10 5	8Ч104	34655,6

Таблица 3. Значения переменных и констант для роликовой опоры типа ГВ для малой роликовой дорожки

r 1	r 2	Δ 1М	Δ 2М	d 1	d 2	d 3	P 1	P 2	J
мм	мм	-	-	мм	мм	мм	Н	Н	Н/мм
14,31	18,32	1,0018	0,9971	8	7,994	7,987	1,3Ч10 5	8Ч104	34655,6

0.3

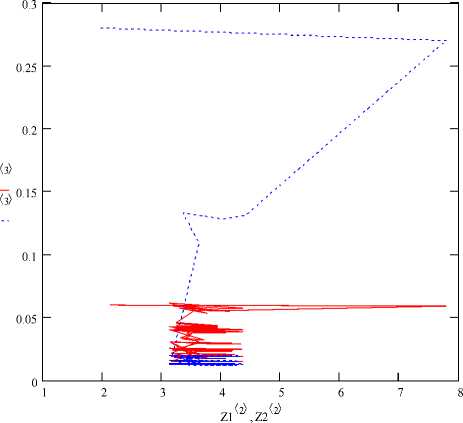
Рис. 3. Фазовые траектории большой роликовой дорожки опоры, собранной по методу структурной упорядоченности с различимыми начальными значениями кольцевых и диаметральных зазоров: Z1, Z2 – начальные состояния сборочных комплектов большой роликовой дорожки для двух вариантов зазоров

0.25

0.2

3 〉

_〉 0.15

3 〉

0.1

0.05

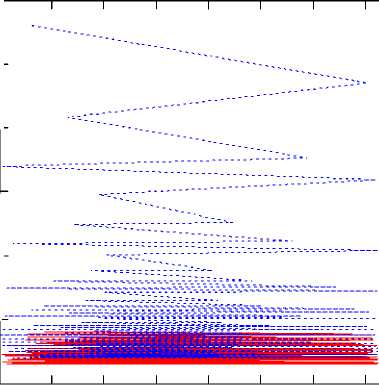
1.5         2         2.5         3         3.5         4         4.5         5         5.5

〈2〉     〈2〉 z1 , z2

Рис. 4. Фазовые траектории малой роликовой дорожки опоры, собранной по методу структурной упорядоченности с различимыми начальными значениями кольцевых и диаметральных зазоров: z1, z2 – начальные состояния сборочных комплектов малой роликовой дорожки для двух вариантов зазоров

комбинаторного варианта четырех схем сборок роликовой опоры бурового долота необходимо предложить критерий качества сборки, характеризующий динамику взаимодействия контактируемых деталей подвижного соединения.

Таким критерием является устойчивость процесса, которая характеризуется относительной амплитудой колебаний

Δ Z = Z max Z min .               (4)

Z max

В табл. 4 представлены численные значения отношений относительной амплитуды ко-

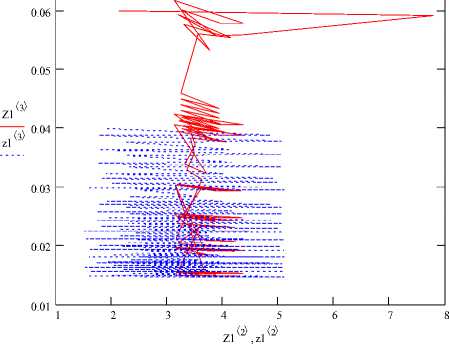
Рис. 5. Фазовые траектории для роликовой опоры при первом варианте сборки:

X1= 2,13 мм, X2= 0,06 мм, х1= 1,92 мм, х1= 0,04 мм

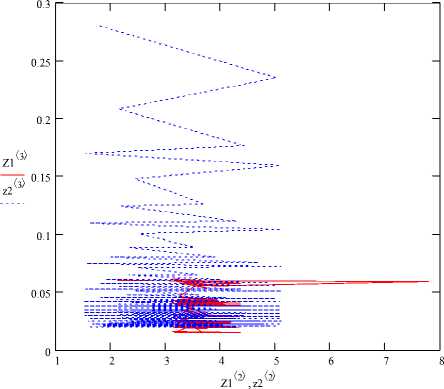
Рис. 6. Фазовые траектории для роликовой опоры при втором варианте сборки:

X1= 2,13 мм, X2= 0,06 мм, х1= 1,8 мм, х1= 0,28 мм

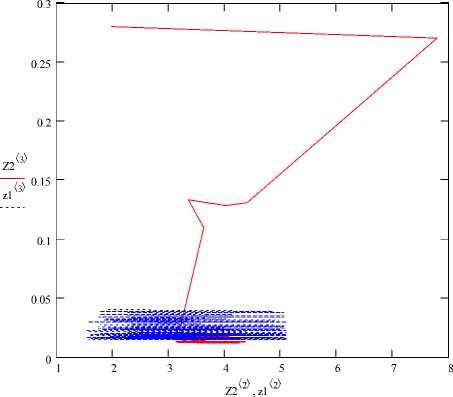
Рис. 7. Фазовые траектории для роликовой опоры при третьем варианте сборки:

X1= 1,98 мм, X2= 0,28 мм, х1= 1,92 мм, х1= 0,04 мм

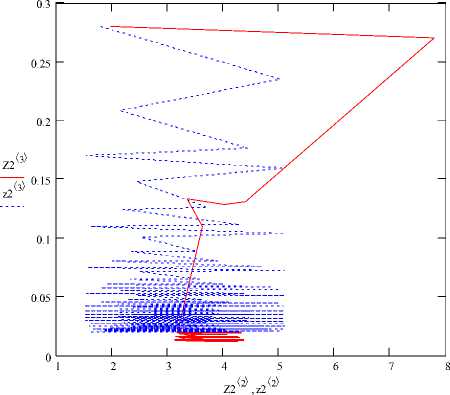
Рис. 8. Фазовые траектории для роликовой опоры при четвертом варианте сборки:

X1= 1,98 мм, X2= 0,28 мм, х1= 1,8 мм, х1= 0,28 мм

Таблица 4. Численные значения отношений относительной амплитуды колебаний большой роликовой дорожки к относительной амплитуде колебаний малой роликовой дорожки

ΔZ/Δz 1 вариант 2 вариант 3 вариант 4 вариант 1,213 0,816 1,531 1,03 лебаний большой роликовой дорожки к относительной амплитуде колебаний малой роликовой дорожки для четырех вариантов сборок.

Как видно из табл. 4 самый устойчивый процесс наблюдается при 2-ом варианте сборки (X1=2,13 мм, X2=0,06 мм, х1=1,8 мм, х1=0,28 мм). Тем самым, собирая роликовые опоры по второму варианту сборки, мы получим наибольший ресурс бурового долота.