Моделирование воздушно-решетной зерноочистительной машины

Еф§м = {F,A,G§[k§m(x),Т§m(х)]}^max ;(1)

AM c Am , F c F, x e Gm (x, u);(2)

be <[bc], bпз <[bпз], §p <[§p].(3)

Здесь F – вектор входных воздействий на принятую в зерноочистительной машине систему операций.

F = {q, aj, W, M (bj), ^(bj ), fQ (B), fQ (H) } ,(4)

А – вектор управляющих факторов системы, обеспечивающих ее функционирование,

^A = {B ш, hn,, Vei, fq (Bn), fv (Вп), Pcx (P), fQx (H ), /qx (B), К §m (х)} .

Векторы входных и управляющих воздействий на пневмосепаратор 1 F и A _П1 , на решетный модуль – F _Р и A _Р , на пневмосепаратор 2 – F _П2 и A _П2 показаны на рис.1.

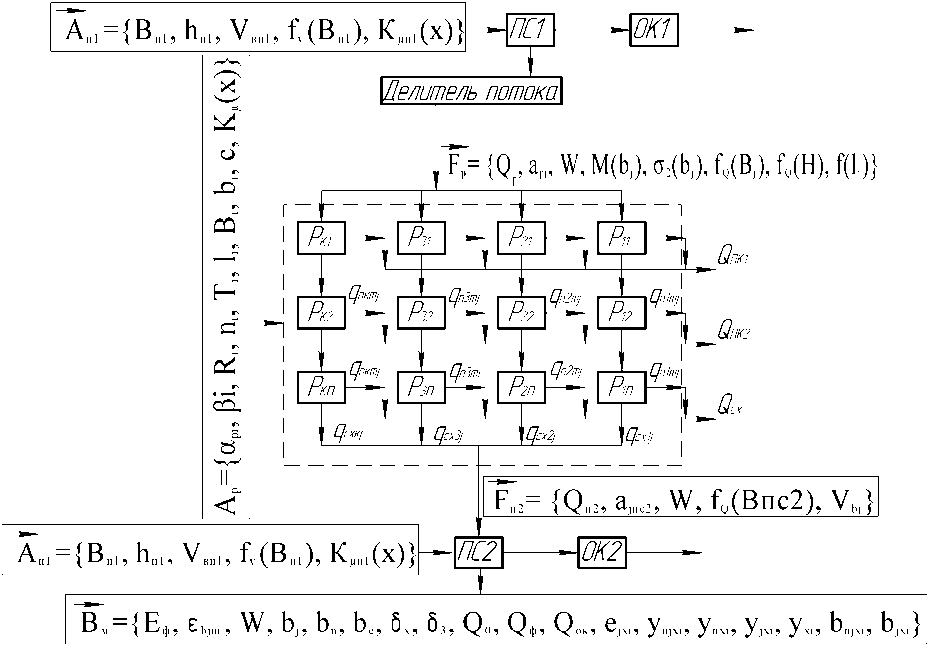
Рис.1. Структурная схема воздушно-решетной зерноочистительной машины с многоярусными решетными модулями

В формуле (1) х - набор технологических операций из G_M ( x , u ) множества, реализуемых в К ₅ м функциональной схеме ВРЗОМ. G ₅ [ К _{5 м} ( х ), T ₅( х ) ] - функционал, определяющий показатели технологического процесса в ВРЗОМ (полнота выделения j-х компонентов, потери зерна, содержание в очищенном зерне других j -х компонентов), для принятой К _{5 м} ( х ) схемы.

Выходные показатели функционирования зерноочистительной машины определяются вектором ВM , независимые аргументы которого случайные в вероятностно-статистическом смысле величины:

В м = { е ф , е bj _ц , w , b j , b _ю, b _с, 5 3 i , 5 з , Q o , Q ф , Q ок , ^е jxi , y n jxi , y n xi , y jxi , y xi , ^b n jxi , ^b jxi } ,

где Еф - критерий эффективности реализации технологического процесса ВРЗОМ; еbjц - полнота выделения из зернового материала отделяемых j-х компонентов; 5зi, 5з - потери зерна на xi операции и общие; Q0, Qф, Qок - масса выхода очищенного зерна, фуражных отходов и отходов разных категорий; ynjxi, ynxi - масса j-х и всех компонентов, содержащихся в зер новом материале после реализации xi -й операции; yjxi,yxi - масса j-х и всех компонентов, выделенных из зернового материала после реализации xi -й операции; bnjxi - содержание j-го компонента в массе очищаемого материала и в выделяемых фракциях bjxi; е jxi -полнота прохода j-го компонента в очищаемый зерновой материал после выполнения xi -й операции.

Ъ-е,

Е ф = 1 - ^ ----,                                (7)

L a j = 2

функция цели:

E ф ^ max .                                  (8)

Обозначения элементов, входящих в выражения (1)-(8), определены в предыдущей работе автора [1].

В общем виде плотность вероятности распределения зернового материала по ширине В пневмоканала и решетного модуля - /q (B), а плотность вероятности распределения скорости воздушного потока в пневмоканале - /V (Bп). Тогда количество зернового материала Qp, попадающего на каждый р-й участок (р=1, 2, …, е) k-й ширины рабочего органа, f/Q (в )dB

Q p = BQ⁰- p - 1 -------,                                (9)

f /q (B )dB p а средняя скорость воздушного потока на р-м участке:

f / v ( B ) dB

Vp = BV p ^{- 1} .                                 (10)

p ke

f /v (B) dB

p

Полнота выхода j -х компонентов зернового материала в очищенное пневмосепаратором зерно:

t Q, ^ ( Q p V )

£   = p '-------------------, nkj          Qe

где enkj(Qp,Vp) - полнота выхода J-го компонента в очищенное пневмосепаратором зерно для ус ловий сепарации, определенных подачей Qp зернового материала и скоростью V, воздушного потока на р-м участке пневмосепаратора e S<2 ,V )= fГQ ,W,a.,MM ,f (B), f (B),B ,h ,f 1,                    (12)

nkj \ p p /           p        j 0 vj v        Q         ni ni ni где MvJ - математические ожидания средних скоростей витания j-х компонентов в исходном материале; Вn, - ширина i-го пневмоканала; hni - глубина i-го пневмоканала; fni- условия ввода зернового материала в пневмоканал.

Конкретные математические модели, определяющие еnkJ для вертикальных пневмокана- лов, пневмосепараторов с активным вводом зернового материала в вертикальный или наклонный пневмоканал определены [1].

При выполнении ограничений (1)-(3) можно рассчитать показатели процесса сепарации:

- содержание сорных примесей (j' =1, 2, ..., с) в очищенном зерне bC = L «^ [^.епJ ; j=C         V j=i          )

( 13)

- полнота выделения ebc пневмосепаратором в отходы сорных (j' =1, 2, „., с) примесей е b c

= t ^[ aj ⁽¹ - ^e п Kj ) ^{] /} ^Laj ' J = C                     j = 1

– содержание j -х компонентов в очищенном зерне

b

= a j ^e C j

b

/ L

V j = 1

I a j ^e п Kj ;

)

– полнота выделения j-го компонента зернового материала в пневмосепараторе ebj =(1-ек);                                          (16)

– содержание j-го компонента зернового материала в легких отходах bo = a J '1 e^. )

;

– масса отходов и масса очищенного в пневмосепараторе зерна b

Q O = L Qa j (1 -е п kj ) , кг/(м - с) ; Q k = Q - Q о , кг/(м - с).                 (18)

j = 1

Построенная математическая модель процесса сепарации гетерогенной сыпучей среды адекватна [2] и позволяет, используя известные методы параметрического и структурного синтеза, проводить многомерный анализ процесса и оценивать рациональные параметры пневмосепаратора для задаваемых условий и ограничений на показатели его функционирования.

Входное воздействие на рассматриваемый решетный модуль выражается вектором Fp, независимые аргументы которого случайные в вероятностно-статистическом смысле величины:

F p = [ Q p , a pj ,W , M ( b ), a ² ( b ), f_Q ( B i ), f_Q ( H ), f ( / i ) ] .                       (19)

Активные средства, определяющие эффективность функционирования решетного модуля, найдем вектором А _р :

Л = [ a p , P i , R i , n, T, l i , B i , b i , c , K , ( x ) ] , (20) где все показатели определены [1].

Различные базовые решетные модули, которые можно использовать в ВРЗОМ, математические модели, описывающие процессы функционирования базовых и комплексных (составленных из различных структур базовых модулей) решетных модулей, определены [1].

Рассмотрим, для примера, в общем случае многоярусный решетный модуль (рис.2) с неоднородными по длине ( 1 ц,... 1 1 _n ) и высоте (1, 2, „., к ) решетами и с различными кинематическими параметрами. В общем виде на ярусы решет поступает q 1 j ,q 2j ,..., q nj ,q _K j количество j -го компонента сыпучего материала с их торцов, определяемое плотностью вероятности распределения f Q ( H ) случайной величины Q (подача сыпучего материала на ярусы (1, 2, „., к решет)) по высоте H расстановки ярусов решет: Q=Q_K (18), содержание j -х компонентов в сыпучем материале b j определяется из выражения (15). Распределение случайной величины q ₅ по ширине В р сепараторов в ярусах определяется плотностью вероятности f ( B ) В качестве допущения здесь и далее будем считать поступление сыпучих материалов на ярусы решет постоянными по времени (процесс квазистатичный) и с равномерным распределением j -х компонентов в сыпучем материале ( j =1, 2, …).

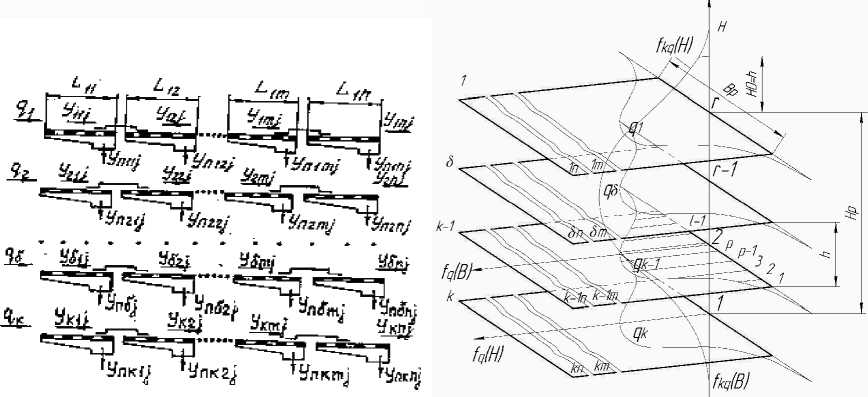
а )                                                      б )

Рис.2. Многоярусный решетный модуль ( а ). Плотность f g ( H) вероятности поступления зернового материала на к - е решетные ярусы и плотность вероятности f 5 _q ( B ) его распределения по их ширине B_p ( б)

Полноту просеивания j -го компонента на 5 -м решетном ярусе можно определить по из- вестному выражению [1]:

p = 1 £ 5 j =

Е q 5 p a j^ ykq 5 p )

q 5 a j l

где    q _{5 p} - приведенная подача сыпучего материала на p -й участок (по ширине B )

BQ

(p = 1,2,..., e) n -го решетного яруса, q5p = ""^"P5Qp ; k=B\e — ширина p -го участка яруса решет; P5qp - вероятность попадания случайной величины Q на p -й участок по ширине

5 -го решетного яруса.

P ₈ Qp = P rQ P 5 pq .                                  (22)

Здесь Р _Г q - вероятность попадания случайной величины Q на Г - ( Г - 1 ) участок ( 5 -й

решетный ярус): Г J f Q ( H ) dH Г - 1 P r Q    С            ; J f Q ( H ) dH Г = 1

J f q ( B ) dB P 5 pq =              -                           (23) J f 5 q ( B ) dB p = 1

При этом подача q5 сыпучего материала на 5 -й решетный ярус q5= QPrQk;                                     (24)

8_{5 j} ( q _{5 p} ) - полнота просеивания j -го компонента на p -м участке 5 -го решетного яруса при подаче q _{5 p} сыпучего материала на этот участок, определяется из различных выражений в зависимости от многих факторов:

85j (q5p ) = f (Q, aj , W, Y, fj , L5m , dm , am , Pm , Rm , Nm , n), где fj, у - вид сыпучего материала (зерно, семена трав и др.) и его плотность; L5m - длина m - го решета 5 -го решетного яруса; d5m - рабочий размер отверстий m -го решета 5 -го яру са; а5m,р5m,R5m,N5m - угол наклона к горизонту, направленность, амплитуда и частота колебаний m -го решета в 5 -м ярусе; n - количество решет в ярусе.

l     jf_Q ( H ) dH J ^f ₅ q ⁽ B ) dB

A Q r----------pr--------5jp (q5p)

^p = ¹ J f Q ( H ) dH j f 5 q ( B ) dB

r = 1                 p = 1

8 5 j —

A q 5 a j

j где 85jp    8(n-1)ojp + [1   85(n-1)ojp ] 85njp .

При известной полноте просеивания 8_{5 j} j -го компонента на отдельном ярусе решет ( 5 = 1,2,..., к ) полнота просеивания j -го компонента на всех ярусах решетного модуля определяется из выражения

k

A q 5 a 5 j ⁸5 j

= 5=1 __________

,

8j"   Qajk где a5j - содержание j -го компонента в сыпучем материале, поступающем на 5 -й решетный ярус.

Сход j -го компонента с p -го участка 8 _m -го решета определяется из выражения

Y, -

8 mpj

m

= q 8 р а₇ П a 8 1 р ^{( h} ) exP

m

—

2y 2B, 202.b, V-_V-L, I 8 i 8 pi ^p8 ij 8 ij 8 ij 8 i

i = 1

V

⁴ q 8 ip

У.

.

Принимая, что для каждого p -го участка и для каждого 8 m -го решета параметры сепарации а _{8 mj} ( h ) , b _{8 mj} , V _{8 mj} различны, но постоянны в пределах ограниченной длины 8 m -го решета, массу просеивания j -го компонента сыпучего материала на длине Х p -го участка 8 m -го решета можно определить из выражения

У

Y n 8 mj ( X ) = Y 8 ( m — 1)/

^{1 —} a 8 mj ^{( h ) e} xP

—

^Y 8 m 8 m ^p8 mj 8 mj

V

{Z Y .( m —O j

У У

а полноту просеивания j -го компонента на длине l 8 m -го решета модуля - из выражения

l

^^, q 8 mp a 8 mj ⁸8 mj ⁽ q 8 mp , ^L )

_        P = 1

8 8 mJ

J f Q ( H ) dH _mi

E Qa 8j --------П(1 — 88 j) aj l j       J fQ (H) dH i=0

8= 1

.

Полнота просеивания j -го компонента 8mj через все m -е решета к ярусов определяется из выражения

k

8 mj = ^ 8 8 mj

8= 1

r

J fQ (H) dH r—1

c

J f Q ( H ) dH

8= 1

.

Полнота просеивания j -го компонента 8j через все решета k -ярусного решетного моду ля

⁸ j = ⁸ ( n — 1 ) oj ^{+ [ 1 — 8} ( n — 1 ) 0 j ] ⁸ nj ,

где 8 ( _{n —} 1 ) 0 j - полнота просевания j -го компонента через все ( n — 1 ) последовательные решета в k ярусах.

Полнота схода 8 _{CX 8 mj} j -го компонента со всего 8 m -го решета

⁸ СХ 8 mj =

q 8 mp a j ⁸ cXmj ⁽ q 8 mp ) p = 1

q 8 m a j l

,

а со всех m -х решет k -ярусного решетного модуля

k

⁸ CXmj = ^ ^P ГQ ⁸ CX 8 mj ^.

8= 1

Полученные выражения (19)-(33) позволяют оценить проход j -х qпδmj и всех qпδm компо- нентов сыпучего материала через δm -е решета отдельных ярусов и всех k ярусов Qпδmj , Qпδm и содержание j-х компонентов в проходе каждого m -го решета δ -го яруса bδmj и всех m -х ярусов bmj [1].

Входное воздействие на второй пневмоканал определяется вектором F _П2 , активные средства – вектором А _П2 (рис.1).

Математическая модель оценки показателей функционирования второго пневмоканала аналогична (9)-(12) при подаче зернового материала в пневмосепаратор 2, равной выходу очищенного в решетном модуле зерна. Проведенные исследования показали, что построенные математические модели с 95-процентной (полнота выделения сорных примесей – 90%) доверительной вероятностью адекватно описывают процесс сепарации в воздушно-решетной зерноочистительной машине [1].

Параметрический синтез. Параметрический синтез функциональной схемы и задаваемой техническим заданием вариации величин аргументов векторов входных F (4) и управляющих A (5) воздействий проводится с использованием соответствующих математических моделей методом нелинейного программирования – методом сканирования с ограничениями, так как отсутствует унимодальность функции цели (8) и нелинейные ограничения (2)-(3).

На втором иерархическом уровне синтезируется функциональная подсистема решетного модуля (РМ) с делителем зернового потока (ДЗП) для ВРЗОМ.

Для синтезированных рациональных параметров рассматриваемой структуры РМ (например, схема РМ, число решетных полотен, форма и размеры отверстий решет, кинематические параметры: частота, амплитуда колебаний, угол наклона решет к горизонту, угол направленности их колебаний) проводится многомерный анализ процесса функционирования РМ при различных величинах вектора выходных F _p (19) и управляющих A _p (20) воздействий, определяемых выходными показателями функционирования ПС.

Эффективность сепарации зерновых (пшеница, рис) и семян подсолнечника с учетом ограничений размеров решетных полотен (ТУ 23.2.2068-89), изготавливаемых в России, а также приводов решетных модулей и систем их очистки от забивания отверстий выявлена для одноярусных трехрешетных модулей.

Определен рациональный решетный модуль с параллельной и последовательной схемами сепарации зернового материала, функциональные показатели которых соответствуют заданным, для очистки зерна с учетом проведенного параметрического и структурного синтеза комплексных решетных модулей [1]

С использованием математической модели (1)-(33) был разработан алгоритм программ для ЭВМ ПК, позволяющий проводить параметрический синтез (8) с учетом принятых ограничений (2)-(3) и значений аргументов векторов F , А , A _p, B_м [1].

Для проведения многомерного анализа оценки основных показателей функционирования обоснованного варианта ВРЗОМ (рис.3) при вариации аргументов вектора F (рис.1) осуществлено моделирование процесса системной сепарации зерна.

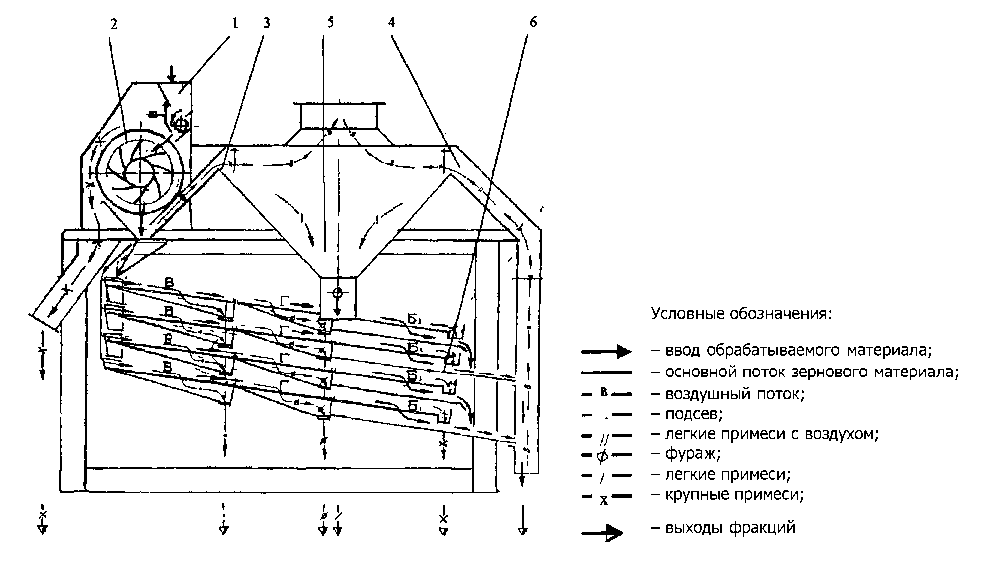
Рис.3. Технологическая схема воздушно-решетной зерноочистительной машины: 1 – камера приемная; 2 – скельператор барабанный; 3, 4 – каналы аспирационные;

5 – камера осадочная; 6 – 4-ярусный решетный модуль

При моделировании приняты следующие допущения: плотность распределения вероятности поступления зернового материала по ширине решетного модуля подчиняется нормальному закону с коэффициентом вариации 20,26%; плотность вероятности распределения зернового материала по высоте решетных ярусов характеризуется коэффициентом вариации X q ( H ) , изменяющимся в пределах от 0 до 54,4%.

Результаты моделирования. Выявлено (рис.4, а ), что в рассмотренном интервале подач изменение коэффициента вариации неравномерности поступления зернового материала на отдельные решетные ярусы несущественно влияет на выделение из него крупных сорных примесей и дробленой соломы.

Полнота выделения мелких сорных примесей s„ (рис.4, 6 ) в интервале подач от 2,775 до в см

4,635 кг/с незначительно уменьшается при изменении коэффициента вариации от 0 до 54,41%. Для интервала подач 4,635-8,58 кг/с sB незначительно снижается при изменении коэффициента см вариации от 0 до 23%. При дальнейшем увеличении Xq(H) происходит существенное снижение полноты выделения мелких сорных зерновых примесей. Агропоказатель bc< 1% (bc - содержание сорных примесей в очищенном зерне) выполняется на всем рассматриваемом диапазоне вариации подач Q и Xq(H) (рис.5,а).

Существенное влияние изменения коэффициента Xq(H) и подачи оказывают на выделение из рассматриваемого материала зерновых примесей sвпз на всем интервале изменения подач. Например, для Q = 3,705 кг/с при изменении Xq(H) от 0 до 54,4% sвпз снижается на 5%, а для Q = 8,115 кг/с при изменении Xq(H) в том же интервале sвпз снижается на 7%. При этом агропоказатель bПЗ< 2% (содержание зерновых примесей в очищенном зерне) выполняется при различных значениях Xq(H) для разных подач. Так, при Xq(H) =24% максимально допустимая по- дача составляет 6,495 кг/с (23,2 т/ч). Для Q = 5,65 кг/с и более увеличение Xq(H) существенно влияет на потери зерна в фуражные и неиспользуемые отходы. Так, для Q = 6,495 кг/с макси мально допустимое значение Xq(H) составляет 35,66%, а для Q = 8,115 кг/с Xq(H)max = 18,1%.

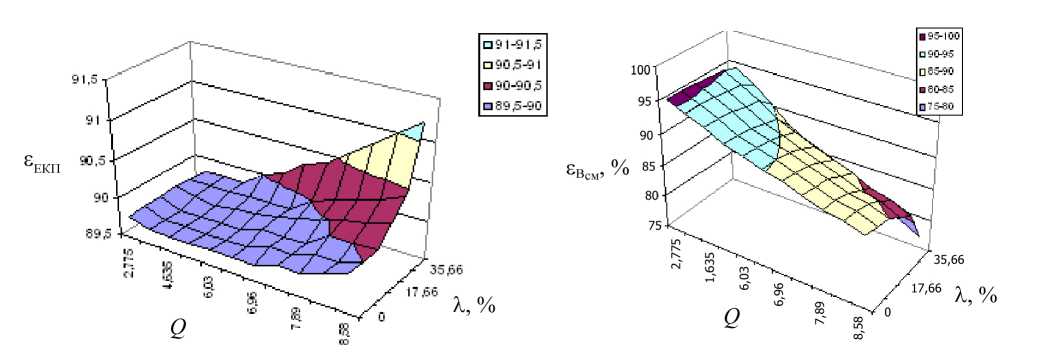
Рис.4. Зависимость полноты выделения компонентов из зернового материала, очищенного воздушно-решетной машиной от подачи Q зернового материала в машину и величины коэффициента вариации X неравномерности поступления зер нового материала на отдельные решетные ярусы: а - крупных £вкп и б - мелких сорных £„ всм

Выявлена усредненная допустимая неравномерность поступления зернового материала на решетные ярусы в пределах Xq(H) =28-30%. При синтезе основных параметров зерноочистительной машины для различных основных величин Q и /q (H) усредненные рациональные па раметры: Vb = 6 м/с, n = 7,92 об/с, Ь1 = 1,7 мм, b2 = 2,0 мм, b3 = 3,6 мм.

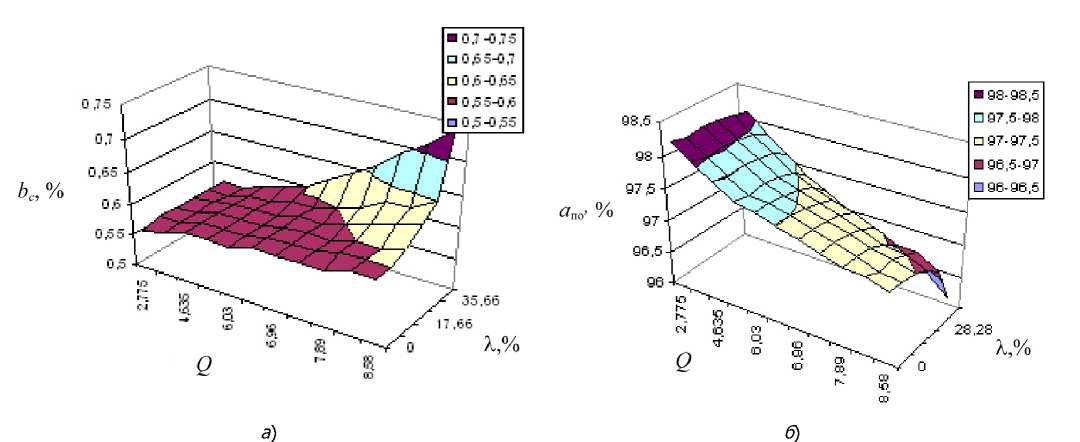
Рис.5. Зависимость содержания в зерне, очищенном воздушно-решетной машиной, сорных примесей bс (а) и чистоты aпо (б) зерна от подачи Q зернового материала в машину и величины коэффициента вариации X неравномерности поступления зернового материала на отдельные решетные ярусы

Выводы. Проведенное моделирование с использованием методов параметрического синтеза позволило проанализировать количественные зависимости показателей функционирования воздушно-решетной зерноочистительной машины при широкой вариации факторов, воздействующих на этот процесс для принятых условий и технологических ограничений, и синтезировать основные параметры ее работы [1].