Моделирование ввода излучения в плоские линейные волноводы с помощью дифракционных решёток для новой технологии изготовления волноводных систем

В настоящее время развивается сфера микроэлек-тромеханических систем, основной целью которой является разработка и производство прецизионных датчиков различных физических величин.

Использование микромеханических систем (МЭМС) не всегда возможно из-за жёстких требований к надёжности во взрывоопасных условиях и при измерении физических величин на объектах, движущихся с большими ускорениями. В связи с этим активно развиваются микрооптические электромеханические системы (МОЭМС), обеспечивающие более широкий спектр использования и обладающие преимуществами перед МЭМС.

Так называемые WGM-резонаторы (резонаторы на модах шепчущих галерей) давно известны, но стали исследоваться и применяться в оптике только в последнее десятилетие, так как появилась возможность их технологического изготовления с помощью методов электронной техники. Использование WGM-резонаторов представляет большой интерес для развития МОЭМС, изготовления фильтров, линий задержек, датчиков, детекторов. Для использования WGM-резонаторов необходима технология ввода излучения. Ввод излучения в плоские волноводы при- ведён в работах [1 –8], [15– 17]. Ввод излучения при сближении плоских и кольцевых волноводов осуществлен в [9– 14]. В предлагаемой работе рассматривается технология ввода излучения в плоские волноводы и приводятся конкретные расчёты параметров слоёв и дифракционных решёток для её реализации.

1.    Технология ввода излучения в волновод через дифракционную решетку

Технология изготовления волноводов и WGM-резонаторов, к сожалению, привязана к стандартным пластинам «кремний на изоляторе» ( silicon-on-insulator , SOI). Эти пластины дороги, и для их использования в некоторых случаях, например, ввод излучения в волновод с помощью дифракционной решётки, их придется дорабатывать, напыляя слои для ввода большей толщины. Изготовление нестандартных волноводных систем требует нестандартной технологии. Для изготовления волновода и дифракционной решётки, с помощью которой вводится излучение, надо изготавливать слои разной толщины в едином технологическом цикле. Для дифракционной решётки необходимая толщина слоя, как правило, намного больше, чем толщина волноводного слоя.

Прямой ввод излучения в волноводную структуру в случае плоских волноводов при толщине волновода порядка микрона практически не реализуем с точки зрения дифракционных ограничений, т.к. длина волны больше толщины волновода и составляет 1,5 мкм. Прямой ввод в торец волновода используют обычно в толстых волноводных системах толщиной порядка 6 мкм, сделанных по методу ионного обмена.

Ввод излучения с помощью призмы тоже крайне затруднителен, т.к. требует в стандартном технологическом процессе микроэлектронной техники применения неспецифических операций вклеивания микропризм, организации зазора между призмой и волноводом и в связи с этим очень сложной операции оптической юстировки каждого волноводного сочленения.

Метод ввода излучения в волноводную структуру с помощью дифракционной решётки намного проще. Для этого необходимо подвести световод к волноводу под расчётным углом, например, 30°, с точностью, не требующей прецизионных устройств, и направить свет, выходящий из световода, на широкую часть сходящегося волновода. Все операции могут быть выполнены под микроскопом с увеличением не более 40.

Есть некоторые особенности ввода с помощью дифракционной решётки, которые заключаются в следующем: чтобы технологически было проще попасть в волновод, делается расширение волновода от 5 мкм до размера порядка 50 мкм, с углом расходимости от волновода менее 2°, и на конце этого рупорообразного волновода изготавливается дифракционная решётка, которая занимает не более 20 % от длины рупора. Решётка в первом порядке дифракции направляет излучение в сходящийся волновод, который плавно переходит в рабочий волновод (рис. 1).

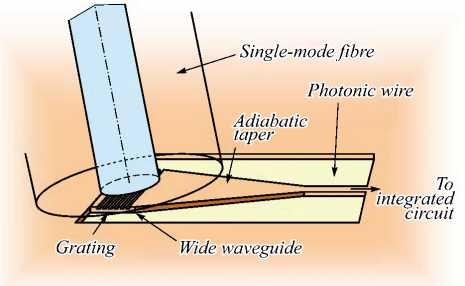
Рис. 1. Схема ввода излучения в волновод при помощи дифракционной решётки [1]

Из-за сложности технологического процесса изготовления дифракционной решётки на краю волновода, а также сложности согласования переходной зоны между дифракционной решёткой и волноводом очень мало работ посвящено этой теме.

Много работ посвящены применению и расчёту резонаторов на модах шепчущей галереи [10– 17]. Технологически волноводные системы в основном изготавливаются на основе кремния, нитрида кремния и двуокиси кремния [1 – 17]. На нитриде кремния по стандартной технологии затруднительно изгото- вить волноводы с толщиной выше 200 нм. Это связано с существенной разницей в коэффициентах расширения этих материалов. Например, при нанесении нитрида кремния толщиной более 200 нм на кремниевую подложку последняя просто начинает деформироваться и из плоской принимает выпуклую шарообразную форму. Нами отработана нестандартная технология нанесения различных волноводных слоёв на кремниевые и кварцевые подложки при низких температурах порядка 200 ° С. Толщины слоёв не ограничены по толщине.

В настоящей статье для этой технологии рассчитаны волноводы, которые будут изготавливаться на кварцевых и кремниевых подложках.

Для 2D-случая были рассчитаны решётки для двух толщин покровных слоёв на ядре волновода: 1 мкм и 3 мкм. Была рассчитана только бинарная структура решётки. Пилообразная структура, где оптимальная высота получается при фазовом набеге через структуру решётки на длину волны λ, пока не рассчитывалась. Теоретически такая решётка может дать эффективность порядка 90%. Пилообразная решётка будет выполнятся в следующих проектах, и для неё, если использовать плавленый кварц, необходима высота покровного слоя над волноводом порядка 3 мкм. Так что выводы, сделанные далее, относятся только к простой бинарной решётке. Также были проанализированы промежуточные значения толщин для бинарной структуры.

2.    Решётка, создаваемая в покровном слое толщиной 1 мкм

Расчёты дифракционной решётки для 2D-случая велись в программе Comsol. Все расчёты проводились для длины волны света 1,5 мкм. Структура волновода с дифракционной решёткой на концах представляла трёхслойную волноводную систему. Тонкий волноводный слой толщиной 70 нм, изготовленный из нитрида кремния Si 3 N 4 , снизу и сверху которого находится плавленый кварц. Снизу от волноведущего слоя имеем кремниевую подложку с высоким качеством полировки, со средней шероховатостью порядка 0,5 нм, сверху – напылённый магнетронным способом слой плавленого кварца, в котором создаётся дифракционная решётка. При моделировании выбирались параметры толщины нижнего слоя 1–3 мкм, так как изготовить слой плавленого кварца на подложке из кремния более 1 мкм составляет определённую проблему из-за разных коэффициентов термического расширения кремния и кварца. У кварца коэффициент линейного расширения в 5 раз меньше, чем у кремния. При технологических температурах нанесения кварца на кремний свыше 500 градусов Цельсия становятся понятными технологические проблемы. При слоях плавленого кварца более 1 мкм на кремниевой подложке толщиной 500 мкм происходит выгибание подложки за счёт её стяжки слоем кварца.

Параметры задавались так, как показано в табл. 1. Структура волновода описана сверху вниз, от воздуха до кремниевой подложки. Оптимальная высота решётки составила 0,8 мкм.

ры×10 – 5. Вверху рисунка показана напряженность электромагнитного поля в / м×10 – 4. На конце решетки, с левой стороны, видно, что излучение уже входит в ядро волновода – структура с большой амплитудой.

Табл. 1. Параметры модели дифракционной решётки

	Показатель преломления	Толщина слоя
Воздух	1	–
Покрытие SiO 2	1,45	~1 мкм
Ядро Si 3 N 4	2	70 нм
Покрытие SiO 2	1,45	0,9–3 мкм
Подложка Si	3,66	500 мкм

xlO"5

2,5    2,0    1,5    1,0     0,5     0

xlO⁴ ■■     :       :       :     -----^™

0,4

0.2

-0,2

0       0,5      1,0      1,5      2,0     2,5 xlO5

Рис. 3. Концентрация световой волны в/м×10– 4 и ввод её в волновод дифракционной решёткой. По оси абсцисс и ординат – расстояние в метрах×10– 5. По мере продвижения волны по решетке концентрация поля

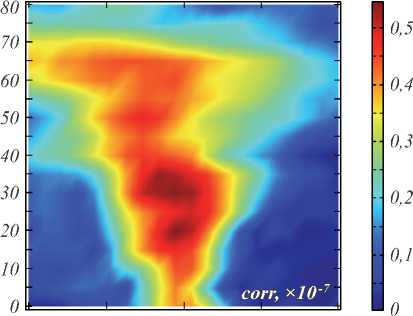
Волноводный слой по расчётам надо наносить на кремниевую подложку с промежуточным слоем из плавленого кварца 900 нм. На рис. 2 по оси абсцисс вправо от нуля показана коррекция увеличения периода решетки, 1 соответствует 0,1 мкм, влево – уменьшение периода решетки. Из расчётов, показанных на рис. 2, мы видим, что оптимальный угол падения луча на решётку лежит в районе 17...23 градуса либо в районе 27...35 градусов. Угол падения в 27...35 градусов более предпочтителен, т.к. расширяются пределы технологических погрешностей периода дифракционной решётки. В последнем случае он составляет примерно 50 нм. Тогда как в первом случае, при падении луча в 17...23 градуса, погрешность изменения периода решётки не должна превышать 10 нм.

alpha_grad

-2  -10  12

Рис. 2. Зависимость дифракционной эффективности решётки высотой 0,8 мкм для вводимого излучения в волновод от угла падения и периода решётки.

По оси абсцисс метры×10 – 7, по оси ординат – угол падения в градусах. Период решётки 1609 нм (на графике – 0).

Толщина подстилающего слоя между подложкой и волноводом – 900 нм

Распределение электрического поля показано на рис. 3. На рисунке видно, что при падении сверху на решётку световой волны происходит увеличение мощности последней при рассмотрении справа налево. Размерность по осям абсцисс и ординат – мет- увеличивается

Из рис. 2 видно, что эффективность равна квадрату амплитуды отношения электромагнитного поля, вошедшего в волновод, к падающему на дифракционную решётку и равно 0,552 = 0,303. Т.е составляет 30%. Это довольно большая эффективность вводимого излучения в столь тонкий волновод (ядро 70 нм). В торец такого тонкого волновода излучение ввести невозможно. Технология ввода в торец волновода применяется в толстых волноводах толщиной порядка 6 мкм, изготовленных по ионообменным технологиям.

3.    Анализ эффективности решётки при изменении толщины подстилающего слоя от 1 до 3 мкм

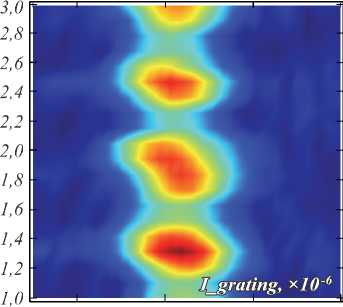
Были проанализированы зависимость эффектив- ности ввода от толщины подстилающего слоя «окись кремния – субстрат», на котором лежит волноводный слой. На рис. 4 показаны несколько расчётных мак- симумов поля в зависимости от толщины подстилающего под волноводом слоя от 1 до 3 мкм.

h_subs, xlO"6

1,4        1,6        1,8        2,0

0,25

0,20

0,15

0,10

0,05

Рис. 4. Зависимость эффективности ввода излучения от периода решётки и толщины субстрата – нижнего слоя, на котором лежит волноводный слой. По оси абцисс период в микронах, по оси ординат толщина слоя в микронах

На рисунке видно, что в области просчитанных толщин существует 4 оптимальных толщины – 1,3 мкм,

1,8...2 мкм, 2,45 мкм, 3 мкм, а также то, что при увеличении толщины слоя эффективность ввода падает. Наилучшей является толщина 1,3 мкм. При этом при технологических отклонениях высоты от 1,21 до 1,41 эффективность ввода будет меняться в пределах 25...30%. Допустимое изменение периода решётки составляет 1,55... 1,7 мкм.

4.    Решётка, создаваемая в покровном слое толщиной 3 мкм

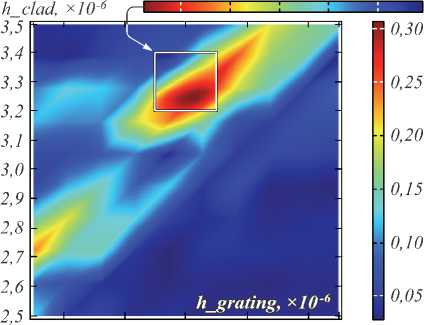
На рис. 5 в укрупнённом виде показано, как влияет толщина слоя покрытия, т.е. верхнего слоя двуокиси кремния над ядром волновода и высоты вытравленной решётки на эффективность ввода. Видно, что максимум достигается при толщине кладдинга 3,25 мкм и высоте решётки 3,05 мкм.

0,25 0,20 0,15 0,10 0,05

2.6    2.8     3.0     3,2     3,4

Рис. 5. Влияние верхнего слоя на ядре волновода h_clad и высоты решётки на дифракционную эффективность вводимого в волновод излучения. Размерность по осям – метры×10 – 6

Мы полагаем, что при большой толщине подложки и покрытия свету проще распространяться в них, чем в ядре. Возможно, при большой толщине клад-динга и глубине решётки в систему кладдинг–ядро попадает и больше света, но в итоге в ядро попадает меньше: пока свет пройдёт 3 микрона до волновода, он, возможно, весь уходит в покрытие, и для ядра уже остается меньше. Математически это тоже понятно, т.к. оптимум для бинарной решётки достигается для полуволнового набега фазы, а для длины волны 1,55 мкм и показателя преломления 1,5 это и составляет 584 нм рассчитанного для кладдинга 1 мкм.

На рис. 5 по вертикали – толщина верхнего слоя (оболочки), по горизонтали – глубина решётки. Максимальная эффективность для электромагнитного поля составила 0,3. Соответственно, для интенсивности света эффективность составит 0,32=0,09=9 %. Сравнивая эффективность с рис. 2, видим, что эффективность при увеличении высоты решётки в 2 раза сильно упала (с 30 % до 9%). Поэтому можно сделать вывод, что оптимальная бинарная решётка должна соответствовать характеристикам, просчитанным на рис. 2.

Заключение

• 1)    Разработана новая, независимая от готовых пластин «кремний на изоляторе» (SOI) технология изготовления плоских волноводных систем. Технология позволяет в одном технологическом цикле изготавливать слои существенно разной толщины, от 70 нм до 3 мкм, что необходимо для изготовления системы «ввод излучения – согласующий элемент – волновод».

• 2)    Промоделирована волноводная система, лежащая на кремниевой подложке и состоящая из ядра Si 3 N 4 толщиной 70 нм, заключённого между слоями SiO 2 толщиной от 1 до 3 мкм с вводом излучения через дифракционную решётку, создаваемую в верхнем слое толщиной 1 мкм. Показано, что оптимальная высота решётки с периодом 1,6 мкм составляет 0,8 мкм. Угол падения луча, при котором достигается максимальная дифракционная эффективность, имеет две оптимальных зоны падения – 17... 23 градуса либо 27... 35 градусов. Эффективность ввода составила 30 %.

• 3)    Промоделирована волноводная система на кремниевой подложке при изменении толщины подстилающего слоя от 1 до 3 мкм. Показано, что в пределах толщин от 1 до 3 мкм имеется 4 максимума эффективности. Максимальная эффективность 9% достигается при толщине подстилающего слоя 1,3 мкм.

• 4)    Промоделирована волноводная система при изменении толщины верхнего покровного слоя от 2,5 до 3,5 мкм. Показано, что при изменении толщины слоя сильно меняется эффективность ввода. Максимальная эффективность 9% достигается при толщине покровного слоя 3,25 мкм.

• 5)    Для получения максимальной эффективности ввода излучения 30 % на кремниевой подложке необходимо изготовить подстилающий слой из SiO 2 толщиной 0,9 мкм, волноводный слой Si 3 N 4 толщиной 70 нм, верхний слой, покрывающий волновод, – 1 мкм; протравить дифракционную решётку с периодом 1,6 мкм в верхнем покровном слое высотой 0,8 мкм. Вводить излучение в одном из двух диапазонов углов падения – 17... 23 градусов либо (что более предпочтительно) в районе 27... 35 градусов. Таким образом, промоделированы все возможные толщины подстилающего и покровного слоёв для волновода толщиной 70 нм и выбраны их значения для получения максимальной эффективности для бинарной дифракционной решётки с шагом 1,6 мкм для длины волны 1550 нм.