Моделирование вычислений на графических процессорах по разностным схемам

Развитие инженерных [1] и научных [2] приложений в новых областях (физика ядра, космические полёты), где применение аналитических подходов ограничено, обусловило всплеск интереса к вычислительной математике в середине прошлого века, сопровождавшийся также бурным развитием компьютерной техники. Появился новый инструмент познания – математическое моделирование, характеризующийся однонаправленной последовательностью «модель, численный метод, программная реализация» [3]. Усложнение в семидесятых годах прошлого века процессорных архитектур (конвейеризация, векторизация и др.) привело часть исследователей [4, 5] к осознанию необходимости учёта архитектурных особенностей уже на стадии построения численного метода.

Однако главенствующая долгое время (до середины двухтысячных) тенденция повышения быстродействия процессоров за счёт увеличения тактовой частоты позволяла научному сообществу игнорировать это соображение. И сейчас зачастую говорят о «распараллеливании» того или иного численного метода [6], понимая под этим исключительно написание параллельной программы или в лучшем случае алгоритма. Такой подход авторы настоящей работы полагают устаревшим.

Действительно, актуальная в последнее десятилетие проблема «кремниевого тупика» [7] вернула исследователей к ситуации, когда повышение быстродействия достигается за счёт усложнения архитектуры вычислительных систем. При этом естественно представить учёт архитектурных особенностей в качестве второго (первый – задачи физики и техники) источника развития численных методов, как это уже было сделано в [4] и [5], но не получило широкого распространения. По мнению авторов предлагаемой работы, для этого полезна запись моделей алгоритмов, моделей вычислительных систем и построение отображения первых на вторые.

Моделирование вычислительных архитектур, алгоритмов и процессов освещалось ранее [8], широко представлено в современной литературе [9,10], но в массовой вычислительной практике встречается редко (в том числе в силу своей сложности) и не признаётся обязательной частью процесса математического моделирования. В предлагаемой статье на типичном примере разностного решения уравнения теплопроводности с использованием GPU демонстрируется насущная необходимость указанного моделирования и предлагается соответствующая модель, отличающаяся от традиционных [9,10] практичностью.

1. Выбор модели алгоритма

Определяясь с объектом моделирования, укажем на существование для GPU достаточно разработанных моделей архитектуры и программных комплексов, неразрывно с такой архитектурой связанных [11]; моделей, весьма удобных программистам при составлении кода по готовым алгоритмам и не вполне полезных специалистам в области вычислительной математики в процессе синтеза алгоритмов в силу перегруженности техническими деталями с одной стороны и отсутствия математического аппарата с другой. Авторы настоящей работы намерены восполнить указанный пробел, записав модель алгоритмов, которые для GPU имеют свою специфику.

Выделим актуальные проблемы, на решение которых такая модель будет ориентирована в случае реализации вычислений на графических процессорах по разностным схемам. За последние 15 лет накоплен достаточно обширный опыт использования GPU в вычислительной практике, чтобы уверенно выделить две основные сложности такого использования: одновременное полное задействование большого количества исполнительных устройств (CUDA ядер) [12] и помещение обширных вычислительных областей в ограниченную (по сравнению с оперативной памятью узла суперкомпьютера) видеопамять [13]. Следова- тельно, модель алгоритмов должна коррелировать с типом DM-SIMD (Distributed Memory Single Instruction Multiple Data) процессорной архитектуры [14], сочетая в себе векторное или матричное представление данных (операции со скалярами нежелательны) и инструменты для коммуникации между разными (распределённой и общей) видами оперативной памяти.

В таксономии Яна Фостера [8] отсутствуют модели алгоритмов, одновременно удовлетворяющие обоим требованиям. Джеймс Ортега [4] детализирует лишь нотацию векторных алгоритмов, к тому же не вполне удобную, по мнению авторов настоящей работы, которые остановили выбор на представлении Джина Голуба из [5]. Последнее использовалось его автором для записи векторных, матричных и параллельных алгоритмов для распределённой и общей памяти. К сожалению, нотация Голуба не вошла тогда в широкий научный оборот, возможно по причине вытеснения языка Linda [15] (частично её использовавшего) библиотекой OpenMP [16]. Так, в более позднем издании [17] Голуб, записывая алгоритмы для общей памяти, переходит к обозначениям, свойственным OpenMP, однако мало пригодным для работы с GPU, при которой коммуникации между оперативной и видеопамятью (а также между различными типами видеопамяти) прописываются в явном виде. Для записи алгоритмов разностного решения дифференциальных уравнений ни Голуб, ни Ортега выбранную нотацию никогда не использовали (авторы предлагаемой статьи делают это впервые), хотя и опубликовали совместную монографию по указанной тематике [17].

Признавая сходство ранней нотации Голуба с синтаксисом языка MatLab (отмечаемое самим Голубом в [5]), предназначенного в настоящее время в том числе и для вычислений на GPU, укажем на различия в области применения этих инструментов. Как будет показано далее, использование выбранной модели в качестве программы хоть и возможно, но не эффективно по сравнению с технологией CUDA.

Проиллюстрируем теперь применение модели Голуба для решения обеих упомянутых проблем реализации вычислений на графических процессорах по разностным схемам.

• 3.     T(2:(N+1)(N+2))=V(2:(N+1)(N+2))+V(N+3:(N+2)²-1);

• 4.     V(N+4:(N+1)(N+2)-1)= α (T(2:N(N+2)-1) +

• 5.     ZeroBorder(V);

• 6.    endfor;

• 7.    put(V, U)

+T(N+5:N(N+2)-1))+V(N+4:(N+1)(N+2)-1);

В алгоритме пересылка значений сеточных функций между GPU и CPU происходит при помощи операторов get (из CPU в GPU в строке 1 передаются значения функции в массиве U , принимаются в V ) и put (из GPU в CPU в строке 7 передаются значения функции в массиве V , принимаются в U ). Общее число узлов сеточной области, включая граничные, выбиралось равным n = ( N + 2)² , где N +2 — число узлов по одному пространственному измерению [12].

На каждом слое timwstep по времени (за перебор N time слоёв отвечает циклическая конструкция – строки от 2-й до 6-й) в соответствии с дифференциальным шаблоном «крест» производятся [12]: вычисление вспомогательного вектора Т (строка 3), расчёт значений сеточной функций из V (строка 4) и восстановление граничных значений (строка 5). Все операции векторные и различаются длиной используемых векторов. При указании элементов в круглых скобках слева от двоеточия указывается первый задействованный элемент вектора, справа – последний. Величина α – константа.

Предваряя моделирование вычислений по алгоритму, укажем на модель процессорной архитектуры, наиболее соответствующую GPU. Согласно [19] графические процессоры классифицируются как SIMT (Single Instruction, Multiple Threads), в которых один набор команд выполняется над множеством потоков, формирующих в каждый момент обработки значения (один поток — одно или несколько значений) результирующего вектора (или нескольких векторов).

Отображая модель алгоритма на модель архитектуры [20], оценим длительность вычислений по векторному алгоритму, принимая это за цель моделирования. Будем оперировать числом потоков num stream s , исполняемых в доступных CUDA-ядрах (один или несколько потоков на ядро). Любая векторная операция в алгоритме при моделировании должна быть разбита на насколько в случае, если размер векторов в ней (пусть m ) превышает num_streams . Тогда длительность одной операции, например сложения двух векторов, можно оценить величиной t add х р m / num streams "| , где t add – время производства скалярной операции сложения, m/num streams – количество таких сложений, выполненных последовательно, р .. "| - операция округления до ближайшего большего целого.

При использовании библиотеки CUBLAS [21] для работы с векторами (в [12] демонстрируется эффективность её применения) необходимо учитывать длительность инициализации ядер и потоков tkernal сопровождающей каждый вызов функции (например, сложения векторов) библиотеки, не зависящей от длины вектора. Тогда, продолжая пример, оценим время сло- жения двух векторов как tke„al+tadd х Гm / Mumstreams "| . Завершая построение отображения, учтём затраты на перемещение данных из CPU в GPU и обратно, приняв их вместе за τCPU/GPU и положив общую длительность одной изолированной векторной операции за tkernal.

Возвращаясь к приведённому выше алгоритму, оценим общее время T его исполнения на GPU как

^{T   T} CPU / GPU + N iime ^X

4xl , + t    ^Г f (TV + 2)2—Й/и um, 1

kernal "add     1 \ J / streams

+

m

ного СКО как

^

m i= 1

эксп T_i

^^^^^^е

мод T_i

эксп T_i

• 100%, где m -

X

^{+ t}add ^{X Г} ( ^N ( ^{N + 2} ) ² ) / num streams 1 ⁺

^{+ t}0 ⁺ t saxpy ^{X Г} ( ^N ( ^{N + 2} ) ^{- 2} ) / num streams 1 V

где первое слагаемое τ CPU / GPU соответствует строкам 1 и 7 алгоритма, множитель N time – количеству итераций циклической конструкции (строки 2–6), в которой 4 раза (4 х t_kernal ) производятся векторные операции: сложение двух векторов размера ( N +2)²-1 (строка 3), сложение векторов размера N ( N +2)-2 (строка 4, правая часть, первое выражение в скобках), saxpy [4] над векторами того же размера (оставшиеся действия в строке 4) и восстановление граничных значений (строка 5) длительностью t 0 . Значения величин τ_{CPU / GPU} , t_kernal , t_add , t_saxpy и t₀ определяются экспериментальным путём запуском соответствующих функций библиотеки CUBLAS и могут отличаться для разных видеокарт.

Адекватность представленных моделей алгоритмов, архитектуры и их отображения проверим сравнением с экспериментальными данными из работы [12], относящимися к первому алгоритму с «длинными» векторами для уравнения теплопроводности (алгоритм 1, рис. 2, 3). Здесь на рис. 1 сопоставлены зависимости длительности вычислений по указанному алгоритму, полученные в ходе натурных измерений (экспериментально) и методом математического моделирования (теоретически) по (1).

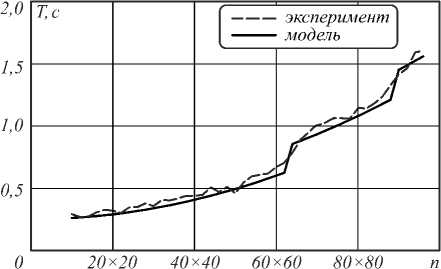
Рис. 1. Сравнение модельных и экспериментальных данных

Величина n варьировалась от небольших значений ( n = 100), соответствующих малой сеточной области 10 x 10 узлов, до величины ( n = 49x10 4 ), определённой размером видеопамяти (2 Гб) карты NVIDIA GeForce GTX 960Ti.

Для оценки отклонения теоретических значений от экспериментальных введём понятие нормирован-

число проведённых экспериментов с n = N × N , меняющейся N от 10 до 7000 с шагом 2 для 10 <  N <  100 и с шагом 20 для N > 100. В рассматриваемом случае (рис. 1) при m =450 данная величина будет равна 5 %, что свидетельствует о хорошем соответствии выбранных моделей объектам исследования (алгоритму и архитектуре GPU).

Наблюдая зависимости длительности вычислений от размера векторных величин, отметим «ступенчатость» обоих графиков, наиболее ярко выраженную для результатов моделирования. В нашем случае первая ступенька на графике приходится на значение в районе n=3600, что хорошо согласуется с архитектурой видеокарты NVIDIA GeForce GTX 980, на которой возможно запускать до 4000 CUDA тредов (для 2048 CUDA-ядер). Далее, с увеличением n, длительность вычислений опять медленно растёт до второй полной загрузки CUDA-ядер.

Объяснение более плавного вида ступенек для экспериментальных данных на рис. 1 авторы связывают, во-первых, с особенностями производства векторных операций на конвейере видеопроцессора (длительность загрузки/выгрузки конвейера в модели не учитывается), про который, в силу закрытости архитектуры CUDA [23], известно не более того, что он существует [19]. Во-вторых, отсутствует инструментарий для контроля загруженности CUDA-ядер, что не позволяет точно оценить аппаратные ресурсы, задействованные при выполнении программы и, как следствие, сделать сравнение теоретических и экспериментальных данных более точным. Таким образом, обсуждая применимость разработанного аппарата, авторы рекомендуют с осторожностью использовать (1) при моделировании для n кратных num streams .

Предложенное описание алгоритмов во многом сходно с синтаксисом языка MatLab, то есть разработанная модель конструктивна. Однако реализовав на MatLab R2012b при помощи пакета Matlab Parallel Computing Toolbox обсуждаемый алгоритм, авторы наблюдали десятикратный рост длительности вычислений по сравнению с реализацией на CUDA, связанный с несовершенством упомянутого пакета, которое отмечалось и ранее [22]. Выбранная в первом параграфе настоящей работы модель предназначена для разработчиков векторных алгоритмов и позволяет математику до программной реализации оценить эффективность вычислений по ним. Создание программного комплекса традиционно производится программистом по готовому алгоритму в соответствии с моделью программирования в CUDA [23] (или другой) и выходит за рамки данной публикации.

3. Расчёт длительности вычисленийпри интенсивном обмене данными между CPU и GPU

Как отмечалось выше, кроме проблемы полной загрузки многочисленных ядер видеопроцессора, при ор-

ганизации вычислений по разностным схемам большое внимание принято уделять преодолению высоких коммуникационных издержек, обусловленных ограниченным объёмом видеопамяти. Традиционно для этого применяются различные варианты метода пирамид [24] («трапеций» в иностранной литературе [25]). Моделирование длительности вычислений по ним, предлагаемое здесь, позволяет заранее выбрать оптимальную высоту пирамиды и является в силу этого важной частью алгоритма. Стремясь проиллюстрировать применение представляемых моделей широким классом примеров (как для явных, так и для неявных разностных схем), авторы начинают изложение с алгоритма из [24], основанного на методе пирамид для решения сеточных уравнений неявной разностной схемы для трёхмерного стационарного уравнения теплопроводности с использованием метода Якоби. В нотации Голуба обсуждаемый алгоритм выглядит следующим образом:

• 1.    (numBlocks, h)=buildPyramids();

• 2.    repeat

• 3.    u=0;

• 4.    for i=1:numBlocks do

• 5.    get (U(0:N-1, 0:N-1, (i-1)×R+1-h:(i-1)×R+R+h), V);

• 6.    get(f( 0:N-1, 0:N-1, (i-1)×R+1-h:(i-1)×R+R+h), fgpu);

• 7.    for j=1:h do

• 8.    V(1:N-2,1:N-2,j:R-j+1)=(1/6) × (V(1:N-2,1:N-2,j-1:R-j)+

• 9.    endfor

• 10.    u=U

• 11.    put(V( 0:N-1, 0:N-1, h:R-h), U(0:N-1, 0:N-1, (i-1)×R+h:(i-1)×R+R-h));

• 12.    endfor;

• 13.    until II ^{м -} U IL < ^£ .

+V(1:N-2,1:N-2,j+1:R-j+2)+V(0:N-3,1:N-2,j:R-j+1)+ +V(2:N-1,1:N-2,j:R-j+1)+V(1:N-2,0:N-3,j:R-j+1)+ +V(1:N-2,2:N-1,j:R-j+1)+α×fgpu(1:N-2,1:N-2,j:R-j+1));

Оперативная память ЭВМ здесь используется для хранения всех значений U сеточной функции, которые, однако, не помещаются целиком в видеопамять и разбиваются поэтому на блоки V (перекрывающиеся). Последние один за другим копируются на GPU (и обратно в строчках 5 и 11), где и выполняется их обработка.

В отличие от алгоритма из пункта 1 сеточные функции здесь трёхмерны, соответственно, трёхмерны и массивы U , V и f , f gpu . Последние два хранят значения правой части решаемого в [24] уравнения в общей (f) и видеопамяти ( f gpu ), копирование данных из первой во вторую производится в строчке 6 алгоритма.

Во внешнем цикле repeat until (строчки 2– 13) производится h итераций по методу Якоби, после чего выполняется проверка условия остановки итерационного процесса (строка 13). При этом за U принимается текущее итерационное приближение, u – предыдущее приближение (строки 3, 10).

Второй цикл (строки 4– 12) предназначен для перебора блоков (общим числом numBlocks, каждый шириной R (где R линейно зависит от высоты пирамиды и максимального объёма доступной видеопамяти) при одномерной декомпозиции и высотой h ), на которые разбита сеточная область. Третий цикл

(строки 7–9) связан с вычислениями h временных слоёв (высота пирамиды) по дифференциальному шаблону внутри блока (строка 8).

Строя отображение данного алгоритма на DM-SIMD архитектуру, примем за t a длительность расчёта одного значения сеточной функции по дифференциальному шаблону, за t_{CPU / GPU} – время пересылки в одном направлении массива из значений сеточных функций размером N ².

В отличие от алгоритма из предыдущего пункта, здесь не производится переход к «длинным» векторам. Для векторов небольших размеров использование функций библиотеки CUBLAS неэффективно, в силу чего величина t kernal более не учитывается. Хранение сеточной функции в многомерном массиве, вместо разворачивания её в один вектор, и непосредственная работа по дифференциальному шаблону делает удобным объединение длительности операций сложения и умножения в одну величину. Переход к трёхмерному случаю обуславливает новую нотацию для обозначения коммуникационных издержек. Как и ранее в пункте 2, все арифметические операции производятся над векторами, которые, однако, все одного размера и длина каждого h ( R-h -1)×( N -2)² не превышает значения num_streams .

Тогда время исполнения одной итерации внешнего цикла можно оценить как

T = nUmBlocks x ( n_ct cpu / GPU I N 2 +n a t a I nUm ,,.^ ) =

= numBlocks x x (3 R - 2 h ) tCPU I GPU +

I

h ( R - h - 1 )( N - 2 ) t a n ^U m r_reads

В табл. 1 приведены названия и значения используемых в (2) и ранее не упомянутых величин.

Табл. 1. Характеристики действий во втором цикле алгоритма

Величина	Значение
Количество отсылаемых (строки 5,6 алгоритма) в видеопамять значений сеточных функций n CPU / GPU	2× R × N ²
Количество принимаемых (строка 11) из видеопамяти значений nGPU / CPU	( R -2 h )× N ²
Общее количество пересылаемых элементов n c = n CPU / GPU + n GPU / CPU	(3 R -2 h )× N ²
Количество значений сеточных функций, вычисляемых по шаблону (в строке 8) na	h ( R-h -1)×( N -2)²

Второй операнд, представленный в виде скобки с двумя слагаемыми, из (2) оценивает длительность одной итерации второго цикла, притом первое слагаемое этого выражения соответствует коммуникационным издержкам, второе – арифметическим.

Моделирование длительности вычислений используется в алгоритме для выбора высоты пирамиды. При вызове функции (первая строка алгоритма) buildPyramids() методом перебора из небольшого числа (10– 15) значений решается соответствующая задача оптимизации. Слишком малые значения h приводят к большому количеству пересылок: например, при h= 1

коммуникации сопровождают переход в разностной схеме к каждому следующему слою по времени, при h =2 коммуникации производятся вдвое реже (хотя данных пересылается вдвое больше, но длительность коммуникаций уменьшается, как видно из рис. 2). Слишком большие значения h приводят к чрезмерному дублированию арифметических операций (на дублировании основан метод пирамид [24, 25]), что видно из (2) и рис. 2.

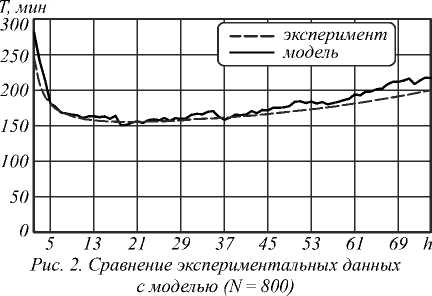
Для выбранных параметров (рис. 2) расхождение экспериментальных данных с результатами моделирования, рассчитанное в соответствии с (2), не превысило 5 %. При дальнейшем росте высоты пирамиды ( h >80) упомянутое расхождение увеличивается, в силу чего авторы рекомендуют использовать модель для оценки высоты пирамиды на интервале 2< h <  N /10, который во всех проведённых экспериментах (включая представленный на рис. 2, где оптимальная высота пирамиды h =20) достаточен для решения поставленной задачи оптимизации.

Заключение

Представленные в работе модели алгоритмов, вычислительных систем и их отображения авторы рекомендуют использовать при организации вычислений по явным и неявным разностным схемам на графических процессорах. В частности, для выбора оптимальной длины вектора в алгоритмах с «длинновекторным» представлением (что позволяет обеспечить рациональную загрузку CUDA-ядер) и отыскания высоты пирамиды, когда используется соответствующий метод построения параллельных алгоритмов (с целью минимизации коммуникационных издержек).

Работа выполнена при поддержке Министерства образования и науки РФ, а также грантов РФФИ (№ 14-07-31178мол_а, №14-01-31305мол_а и №14-07-00291А).