Моделирование высокотемпературного конструкционного материала на основе керамики SiC, армированной углеродными нанотрубками

Стенки неохлаждаемых камер сгорания жидкостных реактивных двигателей малой тяги (ЖРДМТ) при эксплуатации нагреваются до максимально высоких для используемого конструкционного материала температур . Чем выше температура в камере сгорания, тем выше тех- нические характеристики двигателя . Поэтому стоит задача разработки материалов, сохраняющих высокие прочностные характеристики при как можно более высоких температурах .

Керамики являются перспективным классом высокотемператур-ных материалов. Известно, что армирование керамик углеродными на-нотрубками (УНТ) приводит к увеличению как предела прочности на изгиб, так и трещиностойкости [1]. В связи с этим представляет боль-шой интерес исследование возможности применения армированных УНТ керамических композитов в качестве, например , конструкционно-го материала камеры сгорания ЖРД.

В настоящей работе изучается деформирование исследуемого ма-териала, находящегося в условиях стационарного силового и темпера-турного воздействий, соответствующих эксплуатационным режимам типовой камеры сгорания ЖРД. Рассматривается нанокомпозит на ос-нове карбида кремния с размером зерна 250 нм, армированный угле-родными нанотрубками (SiC-УНТ). Эффективные физико-механичес-кие характеристики композита предлагается рассчитывать в рамках прикладных градиентных моделей теории упругости [2‒4]. В результа-те предлагается процедура прогноза эффективных характеристик ке-рамического материала:             , модуля сдвига, коэффициента температурного расширения (КТР), коэффициента теплопроводности и предела прочности.

• 1.    Моделирование эффективных термоупругих характеристик керамического зернистого материала, армированного углеродными нанотрубками

Известно из экспериментальных исследований, проводимых при изучении свойств высокотемпературных керамических материалов (см., например, [5, 6]), что в спечённой керамике, армированной УНТ, нанотрубки располагаются вокруг зёрен, образуя пространственную каркасную структуру . При этом существуют технологии, позволяющие добиться равномерного распределения УНТ по объёму керамики и плотного межзёренного контакта. Поэтому будем предполагать, что рассматриваемый композиционный материал состоит из двух компо-нентов :                                            , между которы- ми реализуется идеальный контакт. Пористость присутствует только внутри зёрен керамики. Исходные физико-механические характери-

[5‒13]

. 1.                     ,

,                                                            -

.

Физико-механические характеристики составляющих композита

Характеристики	УНТ		SiC
	25	2000	25	2000
, ,	1	0,8	0,44	0,33
,	0,16		0,3
, ∙10‒6 ‒1	7,3	13	4,7
Коэффициент , k , /( ∙ )	3000	500	42	10
, B ,	30	15	0,6	0,35

SiC, -

,-

.-

:

,

D ;

d                                                      ().

,                                                                                                                             ,-

,                                                        .-

, близки свойствам углеродной нанотрубки.

-

,

[14, 16]:

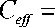
_{1 2}( D d ) ²

d D ^{( 1    2)}

^{1      2} ( ₁ ) th( d ) ( ₂ ) th( D )

eff ‒                                                                                              -

(      ), 1, 2 ‒ фаз (керамики и УНТ) (ГПа), к - градиентный параметр модели, связанный в рассматриваемой задаче с локальным изменением морфологии ке-рамических зёрен в области контакта с УНТ (1/м). Будем предполагать, что зависимость эффективных различных эффективных модулей может быть приближённо описана одним значением градиентного параметра, хотя в общем случае значения могут различаться.

Отметим, что выражение (1) сводится к классической формуле смеси при к—> /:, что соответствует отсутствию изменений в морфологии зёрен керамики при контакте с УНТ:

, _ С 1С₂( D + d ) ef” С, d + С₂ D

.

При определении эффективных модулей упругости композита учтем влияние пористости на значения исходного модуля упругости керамических зёрен. Используя теорию сред с сохраняющимися дислокациями [4], можно показать, что влияние пористости в среде приводит к уменьшению объёмного модуля среды и может быть учтено по следующей формуле:

K 1 “ K 1 (1 K n f )

где K 1 - объёмный модуль пористой керамической фазы, K 1⁰ - модуль беспористой керамики, f ^п - объёмное содержание пор, К_п - коэффициент взаимовлияния деформаций пор и сплошного материала среды, который по своему смыслу является дополнительным физическим мо-дулем модели.

Заметим, что в справочниках [7, 8] приведены соотношения для учета пористости, которые аналогичны уравнению (3).

Предположим, что коэффициент Пуассона зёрен керамики незначительно зависит от объёмного содержания пор (для объёмной доли пористости менее 10 %). Тогда влияние пористости на модуль Юнга и сдвига может быть рассчитано с использованием стандартных формул связи модулей упругости:

E 1 = 3 K 1(1-2V1), G 1=3 K ₁(1-2v₁)/(2+2v₁).

Здесь E 1, G 1 ‒ модуль Юнга и модуль сдвига зёрен керамики, K ₁ ‒ объ-ёмный модуль зёрен, найденный по формуле (3).

Эффективный коэффициент температурного расширения компо-зита, в первом приближении, предлагается определять по классической формуле Левина [15]

< ! !

а1 -ОС2   11

ОС eff =ос₂     12

eff 2  1 / K 1 -¹ / K 2 K_eff K ₂

где K 1, K 2 ос1,ос 2 ‒ объёмные модули и КТР зёрен керамики, и УНТ со-ответственно. K_eff Eeff Geff /(9 Geff 3 Eeff )‒ эффективный объёмный модуль, модули ‒ вычисляются по формуле (1).

Учёт градиентных эффектов при определении Keff приведёт в итоге к учёту масштабных факторов при определении эффективного КТР нанокомпозита. Отметим также, что учет пористости осуществля-ется через зависимость объёмного модуля K ₁ от f ^п (3).

2.    Градиентная модель теплопроводности. Определение эффективного коэффициента теплопроводности

В данной работе предполагается также вычислить и эффективное значение коэффициента теплопроводности, используя вариант гради-ентной теории теплопроводности. Постановка задачи теплопроводно-сти , позволяющей учесть масштабные эффекты, осуществляется с ма-тематической точки зрения аналогично постановке задачи градиентной теории упругости. Лагранжиан модели градиентной теплопроводности может быть записан в виде

LW- E, где

W = [ f^G Ф dV + j f^9G Ф dV ' , E (Ф ) ¹ ₂ [ k (|УФ|²+ C ¹|v^{2 2} dV . G            9G G

Здесь k ‒ коэффициент теплопроводности, Ф ‒ температура, (fG,f G) ‒ обозначают заданное в объеме G и на поверхности 6G скалярное поле (плотности тепловых источников). Легко установить, что использование вариационного принципа дает здесь следующее ва-риационное уравнение модели:

б L- -^к У²У2Ф + f^G |5Ф dV +

C

G

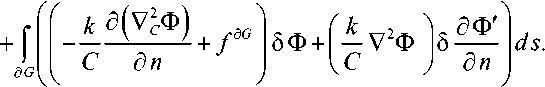
В результате вариационная постановка (6) дает следующее разрешающее уравнение для градиентной теплопроводности:

-( к / С )V²V ²_СФff^G =0, У | Ф = У²Ф- С Ф.

Кроме того, вариационное равенство (6) в случае контактной задачи теплопроводности дает следующие условия контакта на границе двух фаз (скобками обозначается скачок функции на границе контакта):

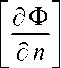
=[ м (ф)]=[ е (ф)]=«.

где M (Ф) = ( к / С )У²Ф, Q (Ф) = -( к / С )—(V C ®).

n

Заметим, что четвертое из записанных выше условий определяет условия непрерывности для обобщенного теплового потока. Оно сводиться к классическому условию, когда С —> со :

V С Ф=У²(Ф)- С Ф, то есть

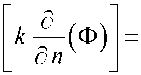
Учитывая (6), легко установить, что в случае одномерной постановки задача градиентной теплопроводности аналогична проблеме градиентной упругости. Поэтому для определения эффективного коэффициента теплопроводности керамики можно воспользоваться ана-логом формулы (1) с заменой упругих констант на коэффициенты теплопроводности фаз:

к = keff

к 1 к ₂( D + d )

к 1 d + k ₂ D-

_____________ ( к -к 2)² ______________

( к jr^r)/th(r ^т d ) + ( к ₂x'^r)/th(x' ^TD )

где keff ‒ искомый эффективный коэффициент теплопроводности ком ^-11; k ₁, k ₂ ‒ коэффициенты теплопроводности фаз

(керамики и УНТ)       11; кг ‒ градиентный параметр модели, определяющий масштаб градиентных эффектов по отношению к тем-пературному воздействиию в области контакта керамических зёрен с УНТ ( 1 /м) .

Отметим, что формула (6) также сводится к классическому выраже-нию для эффективной теплопроводности в случае кт —> оо и имеет вид keff

k ₁ k ₂( D+ d ) k ₁ d + k ₂ D

3.    Об оценке прочности композита SiC-УНТ

Керамические материалы, в том числе армированные УНТ, почти не обладают пластическими свойствами. Поэтому можно считать, что прочность рассматриваемого композита определяется прочностью «слабой» фазы. В нашем случае будем считать, что прочность керами-ки определяется прочностью зерна. Будем предполагать, что разруше-ние рассматриваемого конструкционного керамического материала на-ступает в том случае, когда полные напряжения (рассчитанные с уче-том градиентных эффектов) в зёрнах керамики достигают предела прочности.

На первом этапе решается задача уточнённого определения на-пряжённо-деформированного состояния в рамках одномерной поста-новки градиентной модели с учётом локальных градиентных эффектов. Контактная задача в рамках одномерной постановки градиентной тео-рии упругости имеет следующий вид.

Уравнения равновесия в фазе зерна (от 0 до D ) и фазе нанотрубок (от D до D+d ):

0 x d:         о   m0,

1      1(9)

dxd+D:   о1 m1

:

при x = 0

е о 1 - m^ = p, mi = 0, при x=D+d

о₂ - m 2' = p , m ₂ = 0.

Условия контакта фаз при x = d записываются в виде

У — У r1     r2

r = Г2,

₀1 - m f = o₂ -m 2 , m1 = m ₂.

В приведённой постановке использованы следующие обозначе-ния: r 1 =r i( x ), r ₂ =r ₂( x ) - перемещения в фазе УНТ и в зерне керамики соответственно; о 1, о₂ - классические напряжения в фазе УНТ и в зерне керамики; m 1, m ₂ - моментные напряжения в фазе УНТ и в зерне керамики ; p - внешняя заданная распределённая нагрузка (растягивающие напряжения).

Соотношения закона Гука для классических и моментных напря-жений в рамках градиентной модели имеют вид [16]

E о . i\r .   m^^r,    (i = 1,2)-                 (13)

к,

В записанных уравнениях (9)-(13) величины с индексом 1 относятся к фазе зёрен керамики, а величины с индексом 2 относятся к фазе УНТ.

После решения задачи (9)-(13) в перемещениях напряжения в фазах композита находятся по формулам (13). Далее находим внешние усилия p , при которых в зёрнах керамики наступает разрушение, то есть выполняется условие

• 1    ^В 1^.

Найденное значение р будет определять предел прочность компо-зита оВ. Отметим, что внешние усилия являются параметром задачи. Предельное значение этого параметра может быть найдено в аналити- ческой форме. В отличие от классической теории упругости в рамках градиентной теории напряжения в последовательно соединённых фа-зах не будут постоянными и равными внешним напряжениям. Вслед-ствие влияния градиентных эффектов, концентрирующихся в области границ фаз, напряжения будут отклоняться от классического распреде-ления . Характерный вид распределения полных напряжений (13) в рамках градиентной модели представлен на рис. 1. При этом выпол-няется условие непрерывности классической части напряжений (12), которые входят в постановку контактной задачи.

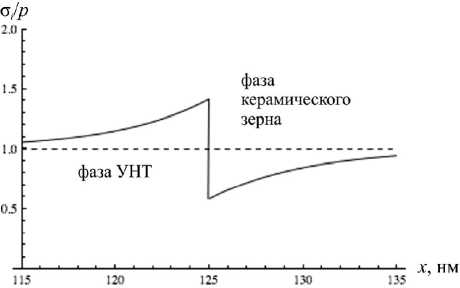
Рис. 1. Характерное распределение напряжений в области контакта фаз. Сплошная линия ‒ градиентная модель, пунктир ‒ классическое решение

Из рис. 1 видно, что в рамках градиентной модели напряжения в керамическом зерне ниже уровня напряжений классической модели и, следовательно, предел прочности в данной фазе будет достигнут при более высоком уровне внешних напряжений. Таким образом, модель позволяет прогнозировать повышение предела прочности композита.

Следует учесть, что прочность керамических зёрен с увеличени-ем объёмной доли пористости снижается. Известны различные эмпи-рические зависимости предела прочности от значения пористости [7]. Для первичных оценок будем использовать линейную зависимость

• 0 /I _ □ £П

4.    Результаты численных вычислений

О B 1 = ст B 1 ( 1 3 f ) .

Здесь о B 1 ‒ предел прочности керамики без пористости ^, приведённый в табл. 1, О B 1 ‒ предел прочности керамической фазы с учётом порис-тости . Коэффициент 3 в записанной выше формуле принят для кера-мики на основе SiC [7].

Для численных вычислений были приняты исходные данные, при-ведённые в табл. 1,                                                   :

‒ керамика с субмикрокристаллической структурой D 250нм ;

‒ K ч = 3 ‒ коэффициент влияния пористости на упругие свойств керамики (см. (3);

‒ к = кг = 0,005нм ‒ параметр градиентности среды. Можно по-казать [17], что данное значение к соответствует протяжённости ло-кальных эффектов в 160 нанометров в зёрнах керамики диаметром 250 нанометров .

На рис. 2‒4 показаны зависимости эффективных упругих харак-теристик, эффективного коэффициента температурного расширения и эффективного коэффициента теплопроводности от объемной доли углеродных нанотрубок и пористости. Исходные характеристики ком-понент композита взяты при 2000 °С. Отметим, что полученные зави-симости не могут быть получены в рамках классических теорий упру-гости и теплопроводности. Эти зависимости и построенная методика расчета в целом (см . (2) и (7)) учитывают размер зёрен керамики и гра-диентные эффекты. Исследовано влияние внутризёренной пористости (до 10 %) на характеристики композита.

На рис. 2 на основе выражения (1) и с учётом (3) и (4), построена зависимость эффективного модуля Юнга и модуля сдвига композита SiC-УНТ от объёмного содержания УНТ ‒ f .

Еф Сф ТПа

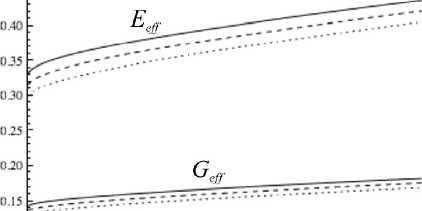
Рис. 2. Зависимость эффективного модуля Юнга E eff и эффективного модуля сдвига G eff композита SiC-УНТ от объёмного содержания УНТ для различных значений пористости:        f^п = 0; f ^п = 5 %; f ^п = 10 %

На рис. 3 построены зависимости эффективного КТР и коэф-фициента теплопроводности от объёмного содержания УНТ с ис-пользованием выражений (5) и (7) соответственно . На данных гра-фиках приведены также решения, получаемые в рамках классиче-ских теорий.

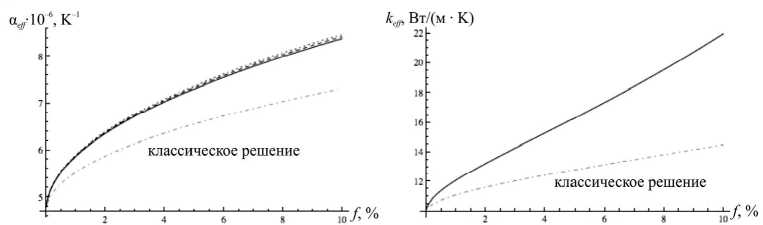
Рис. 3. Зависимость эффективного КТР и коэффициента теплопроводности композита SiC-УНТ от объёмного содержания УНТ :       f ^п = 0; f ^п = 5 %;

f ^п = 10 %

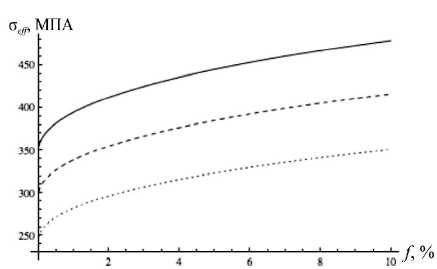
Рис. 4. Зависимость предела прочности композита SiC-УНТ от объёмного содержания УНТ, для различных значений пористости :       f ^п = 0; f ^п = 5 %;

f ^п = 10 %

На рис. 4 показана зависимость предела прочности композита от объёмного содержания УНТ для различных значений внутризёренной пористости. Вычисления предела прочности производились по мето-дике, описанной в и. 3.

5.    Результаты расчёта напряжённого состояния стенки камеры сгорания

В качестве приложения исследовался стационарный тепловой режим камеры сгорания, выполненной из рассматриваемого композита SiC-УНТ . Термический и прочностной расчет стенки камеры сгорания проводился методом конечных элементов в программном комплексе Solid Works. С учетом осевой симметрии задачи рассматривался малый сектор камеры сгорания. Распределение температур на внешней по-верхности стенки камеры в стационарном режиме работы было задано на основе экспериментальных данных, полученных во ФГУП «НИИмаш». Однако амплитудные значения температуры были заданы выше стандартного эксплуатационного режима. Максимальная темпе-ратура модельного случая 2000 °С. Таким образом, входными данными расчёта являлись: , давление га-зов в камере (1 МПа) и физико-механические характеристики материа-ла камеры, найденные с использованием моделирования (см . рис. 2‒4).

Проверка прочности конструкции определялась по третьей тео-рии прочности, наиболее подходящей для использующегося в конст-рукции материала. Основной задачей расчета являлась оценка возмож-ности использования нанокомпозиционного материала для конструк-ций камер сгорания типовых космических двигателей. Критерием такой оценки в расчете являлся коэффициент запаса прочности для мо-дели камеры сгорания.

Для типовой камеры из сплава Нб5В2Мц при заданном распреде-лении температур наиболее опасной точкой является участок камеры сгорания на расстоянии 49 мм от ее основания ‒ в докритической об-ласти, в месте начала уменьшения диаметра цилиндрической части ка-меры сгорания. Данный участок является наименее прочным за счет высокого градиента температуры в этой области, а также за счет гео-метрических особенностей камеры сгорания, а именно геометрически обусловленного концентратора напряжений. Расчёт, проведённый для типовой камеры из сплава Нб5В2Мц показал, что возникающие на-пряжения при заданном распределении температуры превышают пре-дел прочности материала и запас прочности ниже 1, т. . произойдёт разрушение конструкции.

При расчете стенки камеры сгорания из модельного композита SiC-УНТ использовались ранее полученные физико-механические ха-рактеристики (см. рис. 2‒4). Рассматривались материалы с 0, 5 и 10 % пористости и содержанием УНТ 1, 2, 4 и 6 %. Найдено, что и в этом случае максимальные напряжения и минимальные коэффициенты за-паса достигаются в точке на расстоянии 49 мм от основания камеры сгорания. В табл . 2 приведены экстремальные значения напряжения и коэффициента запаса в стенке камеры сгорания для материалов, разли-чающихся величиной пористости и содержанием нанотрубок. В табли-це приведены также рассчитанные значения пределов прочности мо-дификаций композита (ов ) .

Таблица 2

Результаты расчёта напряжённого состояния стенки камеры сгорания

f , %	f , %	а, M a	о max , МПа	Коэффициент запаса
0	1	395	122	2,8
0	2	412	133	2,7
0	4	436	151	2,5
5	1	347	108	2,8
5	2	366	119	2,6
5	4	391	138	2,4
5	6	410	154	2,3
10	1	298	92	2,8
10	2	319	103	2,7
10	4	346	122	2,5

Для всех значений пористости коэффициент запаса больше 2, причём он падает с увеличением содержания УНТ, несмотря на то, что предел прочности материала растёт. Объяснение этому может быть следующее. Основной источник напряжения в опасном сечении ‒ тер -монапряжения . Величина температурных напряжений пропорциональ-на произведению коэффициента термического расширения на модуль упругости материала. Следовательно, величина термонапряжений рас-тёт быстрее с увеличением содержания нанотрубок, чем увеличивается предел прочности. В результате коэффициент запаса падает, а его мак-симальные значения при доле УНТ менее 1 %.

Заключение

В работе приводится последовательность расчёта эффективных значений модуля Юнга, модуля сдвига, КТР , коэффициента теплопро-водности и предела прочности композита на основе карбида кремния, армированного нанотрубками. Используется методика расчёта, учиты-вающая масштабные эффекты, то есть характерный размер зерна и плотность границ контакта. Показано, что все указанные характери- стики растут с увеличением содержания нанотрубок в композите. Про-ведён температурный и прочностной расчет стенки камеры сгорания методом конечных элементов при температуре нагрева, достигающей 2000 °С. Показано , что максимальные коэффициенты запаса (до 2,8) имеют место для композита при малой пористости и содержании на-нотрубок менее 1 %.

Работа выполнена при финансовой поддержке РФФИ (гранты №01-09-00060, №11-01-12081-офим), Программы президиума РАН П-22 и при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России на 2009‒2013 гг.» Гос .контракты № 14.740.11.1326, 14.740.11.0995.