Моделирование взаимодействия виброплиты с поверхностью грунта

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2022PNRPU MECHANICS BULLETIN

Виброплиты в строительстве применяются при уплотнении грунтов в траншеях, пазухах фундаментов и в других местах, где затруднено или невозможно использовать вибрационные катки. Несмотря на то, что виброплиты выпускаются не одно десятилетие и накоплен достаточно большой опыт их практического применения, до сих пор вопрос определения технологических возможностей виброплиты с известными характеристиками при уплотнении грунта в конкретных условиях производства работ не решен. Обзор рекомендаций производителей виброплит [1] показывает, что в большинстве случаев рекомендации носят слишком общий характер и не позволяют определить, например, требуемое число проходов виброплиты с известными характеристиками при уплотнении грунта конкретного вида в слое заданной толщины до требуемого состояния (коэффициента уплотнения). Это связано с недостаточной изученностью процессов изменения напряженно-деформированного состояния грунта при динамических воздействиях, недостаточным объемом данных по численным значениям основных физико-механических характеристик грунтов при изменении вида, плотности и влажности грунта, сложным характером взаимодействий элементов виброплиты между собой и с уплотняемым грунтом, а также другими факторами. Для разработки методики влияния технических характеристик виброплиты на результаты уплотнения грунта в кон- кретных условиях производства работ предлагается использовать подход [2], основанный на условном разделении процесса уплотнения грунта на три фазы: развития контактных напряжений; распространения напряжений по толщине слоя грунта; развития деформаций на различных глубинах грунта.

На характер развития во времени контактных напряжений влияют технические характеристики виброплиты (масса элементов виброплиты, характеристики амортизаторов виброплиты, частота и вынуждающее усилие вибровозбудителя, размеры основания виброплиты) и свойства грунта. Поскольку виброплита представляет собой многомассную колебательную систему, взаимодействующую с деформируемым ограничителем (грунтом), то для моделирования процессов в такой системе целесообразно применять метод реологического моделирования. При этом методе рассматривается поведение точек, в которых сосредоточена вся масса отдельных элементов системы. Связи между этими массами моделируются идеализированными упругими, вязкими и пластичными элементами. Различными исследователями предлагались различные варианты реологических моделей. В работах [3–7] рассматривались одномассные реологические модели, учитывающие только массу рабочего органа [3–6] или рабочего органа вместе с пригрузом от рамы машины [7]. В двухмассных реологических моделях [8–14] учитываются массы рабочего органа и грунта или массы рабочего органа и рамы. В трёхмассных реологических моделях [15–17]

учитываются масса рабочего органа, масса рамы рабочего органа и масса уплотняемого грунта (присоединённая масса грунта).

При моделировании свойств грунта в реологических моделях используются как сравнительно простые модели типа Кельвина – Фойгта [7; 15–19], так и более сложные [20–24]. Наибольшее распространение при реологическом моделировании свойств грунта получила модель Кельвина – Фойгта, сочетающая в себе сравнительную простоту и воспроизведение характерного поведения грунта при динамических нагрузках [25; 26].

В данной работе представлены результаты исследования взаимодействия виброплиты с грунтом с применением трёхмассной реологической модели системы «грунт – основание виброплиты – рама виброплиты» и моделирование упруговязких свойств грунта по схеме Кельвина – Фойгта.

1.    Постановка задачи

Моделирование развития во времени контактных напряжений при уплотнении грунта виброплитой осуществлялось на основании обработки результатов вычислительного эксперимента. Взаимодействие виброплиты с уплотняемым грунтом исследовалось на основе трёхмассной реологической модели. Виброплита рассматривалась состоящей из основания массой m d и верхней части массой m f , связанной с основанием посредством амортизаторов. К основанию виброплиты прикладывалась гармонически изменяющаяся вынуждающая сила P sin ( to t ), где P - амплитудное значение вынуждающей силы, Н; to - угловая скорость, рад/с; t – время, с. Массы основания m d и рамы виброплиты m f принимались равными ( m d = m f ). Амортизаторы виброплиты моделировались параллельно установленными элементами упругого и вязкого сопротивления с коэффициентами k f и b f соответственно. Грунт моделировался массой m s , движение которой ограничивается параллельно установленными элементами упругого и вязкого сопротивления (модель Кельвина – Фойгта) с коэффициентами k s и b s соответственно. Значение присоединенной массы грунта на основании исследований [15; 27] рассчитывалось как m s = 0,2 ·m d . Значение коэффициентов упругого k f и вязкого b f сопротивлений амортизаторов виброплиты рассчитывалось в зависимости от массы виброплиты по зависимостям, полученным в результате статистической обработки характеристик амортизаторов вибрационных машин для уплотнения грунтов.

2.    Теория

Реологическая модель (рис. 1) позволяет исследовать взаимодействие виброплиты с грунтом как в режиме контакта, так и в режимах периодического отрыва от грунта [15; 27].

В режиме контакта с грунтом дифференциальные уравнения движения масс имеют вид:

m f • x f - b f • ( x d - x f ) - k f • ( x d - X f ) = m f • g ; ⁽ m d ⁺ m s ) • ^xd ⁺ b s • ^xd ⁺ b f • ( ^xd ^{- x}f ) ^{+ k}s • x d ⁺ + k f • ( x d - x f ) = ( m_d + m s ) • g + P • sin ( to t ) ; ^xd = x s ;

xd = xs, где xf - ускорение верхней части виброплиты, м/с2; xd - ускорение основания виброплиты, м/с2; bf - коэффициент вязкого сопротивления амортизаторов, соединяющих основание и верхнюю часть виброплиты, Н·с/м; bs – коэффициент вязкого сопротивления грунта, Н^с/м; xf - вертикальная скорость перемещения верхней части виброплиты, м/с; xd - вертикальная скорость перемещения основания виброплиты, м/с; xs - вертикальная скорость перемещения грунта, м/с; kf – коэффициент упругого сопротивления амортизаторов, соединяющих основание и верхнюю часть виброплиты, Н/м; ks – коэффициент упругого сопротивления грунта, Н/м; xf – вертикальная координата верхней части виброплиты, м; xd – вертикальная координата основания виброплиты, м; xs – вертикальная координата грунта, м; g – ускорение свободного падения, м/с2; Р – вынуждающая сила, Н; to - угловая скорость вибровозбудителя, рад/с.

В режиме отрыва от грунта дифференциальные уравнения движения масс имеют вид:

m f • x f + k f • ( x_d - x f ) + b f • ( x_d - x f ) = m f • g ; m d • ^xd ^- k f • ( ^xd ^{- x}f )^{- b}f • ( xcd ^{- x}f ) = = m_d • g + P • sin ( to t ) ;

• m s • x_s + k_s • x_s + b_s • x_s = m s • g .

  
  

Сила реакции грунта на основание виброплиты:

F s = m s • x s + k s • x s + b s • x s - m s • g .           (3)

Условие неприлипания грунта к основанию виброплиты:

F s >  0-                       (4)

Условием перехода от режима отрыва от грунта (системе уравнений (2)) к режиму контакта с грунтом (системе уравнений (1)) и наоборот является равенство вертикальных координат основания виброплиты и поверхности грунта:

x d ^ ^xs -                          ⁽⁵⁾

Для численного решения уравнений (1)–(2) была разработана расчетная модель в среде MATLAB Simulink.

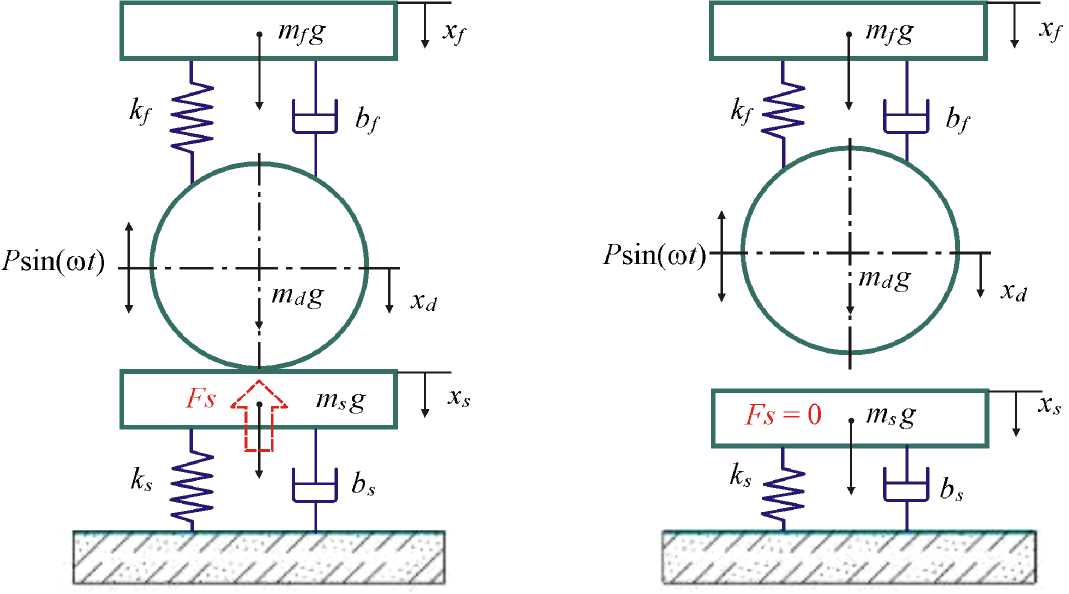
Рис. 1. Трёхмассная реологическая модель взаимодействия виброплиты с уплотняемым грунтом [27]

Fig. 1. Three-mass rheological model of interaction between a vibrating plate and compacted soil [27]

Рис. 2. Экспериментальные исследования уплотнения грунта виброплитой Zitrek CNP 20

Fig. 2. The experimental studies of soil compaction with a Zitrek CNP 20 vibratory plate

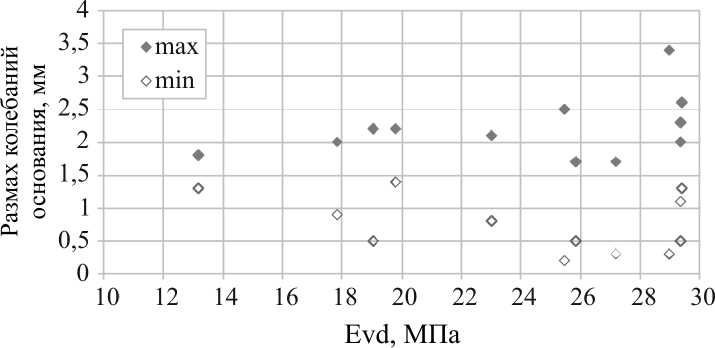
Рис. 3. Экспериментальные значения размаха вертикальных колебаний основания виброплиты Zitrek CNP 20

• Fig. 3.    The experimental values of the vertical base oscillation range of the Zitrek CNP 20 vibratory plate

Верификация разработанной реологической модели осуществлялась на основании сравнения результатов расчета с экспериментальными данными.

Экспериментальные исследования уплотнения грунта виброплитой Zitrek CNP 20 в полевых условиях [28] проводились в августе 2021 г. на одной из строительных площадок г. Ярославля. В процессе исследований регистрировались вертикальные перемещения основания и рамы виброплиты. Регистрация перемещений осуществлялась лазерным датчиком BAUMER OADM 13U6480/S35A, который в процессе движения виброплиты удерживался испытателем на высоте 100–150 мм над исследуемой поверхностью (основанием или рамой виброплиты) (рис. 2), что обеспечивало разрешающую способность датчика 0,25 мм и линейную ошибку измерений не более 0,8 мм.

При частоте колебаний виброплиты 90 Гц время отклика датчика перемещений составляло менее 0,9 мс, что позволяло осуществлять опрос датчика с частотой около 1,1 кГц и обеспечивало не менее 10 измерений вертикального положения поверхности виброплиты в каждом цикле колебаний. Регистрация показаний лазерного датчика перемещений происходила при помощи анализатора спектра ZET 017-U8. Обработка результатов измерений осуществлялась с использованием технологии цифровой фильтрации сигналов в программе ZET ANALIZ с граничной частотой фильтра низких частот 200 Гц. Уплотнение грунта после каждого прохода виброплиты оценивалось значением динамического модуля деформации грунта E vd , измеряемого при помощи установки динамического нагружения ZORN ZFG 3.0. В качестве грунта использовался песчано-гравелистый грунт. Результирующие значения размаха вертикальных колебаний основания и рамы виброплиты Zitrek CNP 20, полученные после обработки экспериментальных данных, представлены на рис. 3, 4.

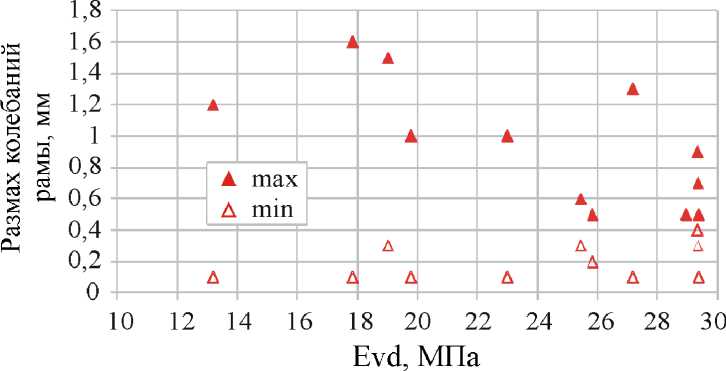
Рис. 4. Экспериментальные значения размаха вертикальных колебаний рамы виброплиты Zitrek CNP 20

• Fig. 4.    The experimental values of the vertical span oscillation range of the Zitrek CNP 20 vibratory plate

При моделировании колебаний основания и рамы виброплиты выполнялись расчеты по разработанной реологической модели для виброплиты с характеристиками, соответствующими характеристикам виброплиты Zitrek CNP 20: масса основания m d = 54,5 кг; масса рамы виброплиты m f = 32,2 кг; присоединенная масса грунта m s = 10,9 кг; вынуждающая сила P = 19,8 кН; частота колебаний 91 Гц; ω – угловая скорость вибровозбудителя ω = 661 рад/с (соответствует частоте колебаний 91 Гц). Значение коэффициента упругого сопротивления амортизаторов виброплиты определялось на основании специально проведенных экспериментальных исследований и составляло k f = 2,11 МН/м. Значение коэффициента вязкого сопротивления амортизаторов определялось с учетом [29] и составляло b f = 3,19 кН ⋅ с/м.

Расчетные значения размаха вертикальных колебаний основания и рамы виброплиты Zitrek CNP 20, полученные на основании разработанной реологической модели, представлены на (рис. 5–6).

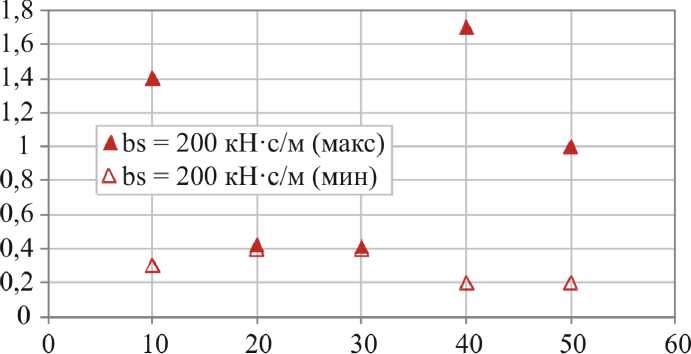
Анализ графиков экспериментальных и расчетных значений размаха вертикальных колебаний основания и рамы виброплиты Zitrek CNP 20 (рис. 3–6) показывает, что в сопоставимых диапазонах изменения свойств грунта (диапазону k_s = 10…50 МН/м при b_s = 200 кН ⋅ с/м соответствует диапазон E vd = 7…33 МПа для песчаногравелистого и супесчаного грунта) расчетные значения размаха вертикальных колебаний основания виброплиты Zitrek CNP 20 находятся внутри диапазона значений, полученных при экспериментальных исследованиях. Расчетные значения размаха вертикальных колебаний рамы виброплиты Zitrek CNP 20 на большей части диапазона согласуются с экспериментальными значениями. Лишь в зоне значений k s ≥ 40 МН/м расчетный размах колебаний рамы незначительно превышает полученные при экспериментальных исследованиях значения.

Таким образом, можно сделать вывод об удовлетворительной верификации разработанной реологической модели взаимодействия виброплиты с уплотняемым грунтом.

Для определения особенностей изменения во времени контактных напряжений при уплотнении грунта виброплитой по разработанной модели был проведен вычис- лительный эксперимент. С учетом исследований [30] в качестве независимых параметров виброплиты была выбрана масса виброплиты m = (md + mf). Значения угловой скорости колебаний ω и вынуждающего усилия P виброплиты рассчитывались в зависимости от массы m [30].

В качестве независимых параметров грунта были выбраны коэффициенты упругого k s и вязкого b s сопротивления грунта.

В табл. 1 представлены значения независимых параметров вычислительного эксперимента. Общее количество сочетаний факторов равнялось 96.

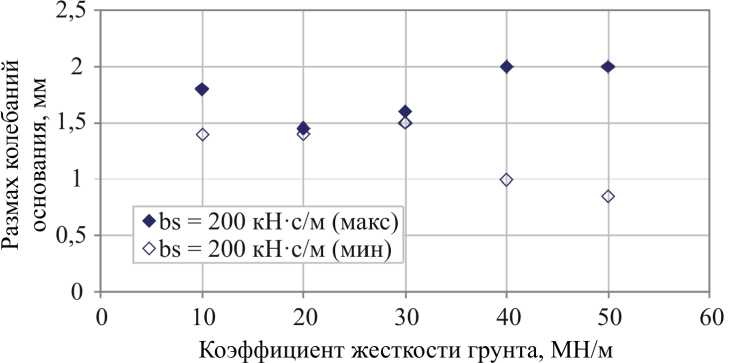
Рис. 5. Расчетные значения размаха вертикальных колебаний основания виброплиты Zitrek CNP 20

• Fig. 5.    The calculated values of the vibratory plate vertical base oscillation range of the Zitrek CNP 20

  
  

S га p.

« К М й ю о ч S £ га

Коэффициент жесткости грунта, МН/м

Рис. 6. Расчетные значения размаха вертикальных колебаний рамы виброплиты Zitrek CNP 20

• Fig. 6.    The calculated values of the vertical oscillation span of the frame of the the Zitrek CNP 20 vibratory plate

3.    Результаты экспериментов

Таблица 1/Table 1

Значения независимых параметров вычислительного эксперимента

Values of independent parameters of the computational experiment

Параметр	Минимальное значение	Максимальное значение	Шаг изменения	Количество значений
Масса виброплиты m , кг	50	750	100	8
Коэффициент упругого сопротивления грунта ks , МН/м	30	120	30	4
Коэффициент вязкого сопротивления грунта bs , кН·с/м	100	300	100	3

В процессе вычислительного эксперимента для соответствующих значений факторов рассчитывались значения угловой скорости колебаний ω , вынуждающего усилия P , значения коэффициентов k f и b f амортизаторов виброплиты, значения масс m d , m f и m s . Затем производился расчет по программе MATLAB Simulink, в результате которого формировались осциллограммы перемещения основания виброплиты и грунта, а также осциллограмма изменения силы реакции грунта F s . Продолжительность расчета составляла 10 с. Для исключения влияния переходных процессов анализ осциллограмм проводился в интервале времени от 9,5 до 10 с.

В зависимости от сочетания значений факторов моделью реализуются различные режимы работы [31] виброплиты: режим постоянного контакта с грунтом (continuous contact) (рис. 7), режим частичного отрыва от грунта (partial uplift) (рис. 8), режим двойного прыж- ка (double jump) (рис. 9), а также более сложные режимы колебаний с кратностью более 1 (рис. 10).

На осциллограммах силы реакции грунта выбирались характерные циклы нагружения, для которых определялись время нагружения грунта (увеличения значений F s ) t ₁, время разгрузки (уменьшения значений F_s ) t ₂, а также максимальное значение силы реакции грунта F s^max . Поскольку на значение деформаций грунта наибольшее значение оказывают действующие напряжения [32], то при анализе осциллограмм выделялись характерные воздействия с максимальными пиковыми значениями F s , для которых и рассчитывались значения t 1 , t 2 и F s^max .

После определения по осциллограммам численных значений времени нагружения грунта t 1 , времени разгрузки грунта t 2 , а также максимального значения силы реакции грунта F_s ^max производилась статистическая обработка полученных результатов в программе STATISTICA для получения регрессионных зависимостей t 1 , t 2 и F s^max (табл. 2). В табл 2. применяются следующие единицы измерения параметров: t₁ , мс; t₂ , мс; F_s ^max , Н; k_s , МН/м; b_s , кН·с/м.

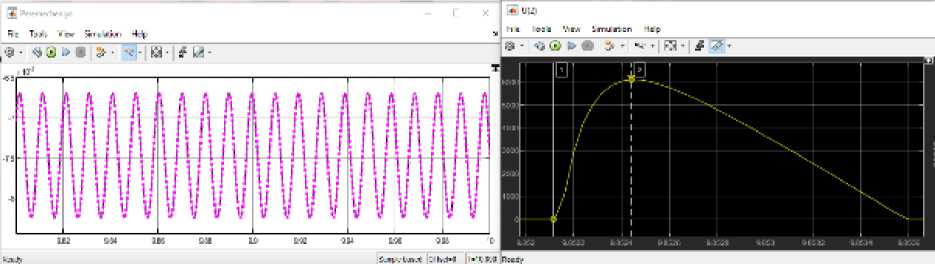
Рис. 7. Осциллограммы перемещений основания виброплиты и грунта, а также силы реакции грунта для характерного цикла нагружения ( k_s = 30 МН/м, b_s = 300 кН ⋅ с/м, m_d = 25 кг, m f = 25 кг, m_s = 5 кг, ω = 641 рад/с, P = 8962 Н, k f = 2,11 МН/м, b f = 3,29 кН ⋅ с/м, режим постоянного контакта с грунтом (continuous contact))

Fig. 7. Oscillograms of the displacement of the of the base of the vibrating plate and the soil, as well as the soil reaction forces for a characteristic loading cycle ( k_s = 30 МN/m, b_s = 300 kN ⋅ s/m, m_d = 25 kg, m f = 25 kg, m_s = 5 kg, ω = 641 rad/s, P = 8962 N, k f = 2.11 MN/m, b f = 3,29 kN ⋅ s/m (continuous contact))

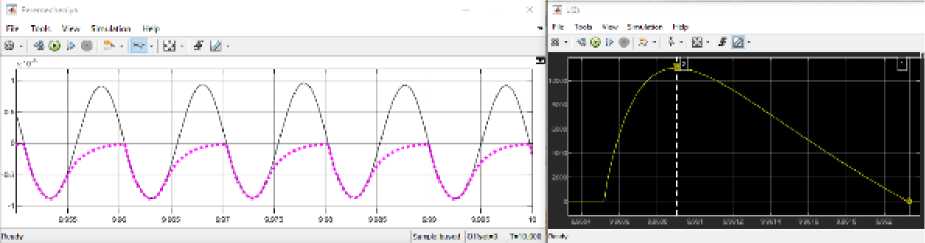
Рис. 8. Осциллограммы перемещений основания виброплиты и грунта, а также силы реакции грунта для характерного цикла нагружения ( k_s = 120 МН/м, b_s = 200 кН ⋅ с/м, m_d = 25 кг, m f = 25 кг, m_s = 5 кг, ω = 641 рад/с, P = 8962 Н, k f = 2,11 МН/м, b f = 3,29 кН ⋅ с/м, режим частичного отрыва от грунта (partial uplift))

Fig. 8. Oscillograms of the displacement of the of the base of the vibrating plate and the soil, as well as the soil reaction forces for a characteristic loading cycle ( k_s = 120 МN/m, b_s = 200 kN ⋅ s/m, m_d = 25 kg, m f = 25 kg, m_s = 5 kg, ω = 641 rad/s, P = 8962 N, k f = 2.11 MN/m, b f = 3,29 kN ⋅ s/m (partial uplift))

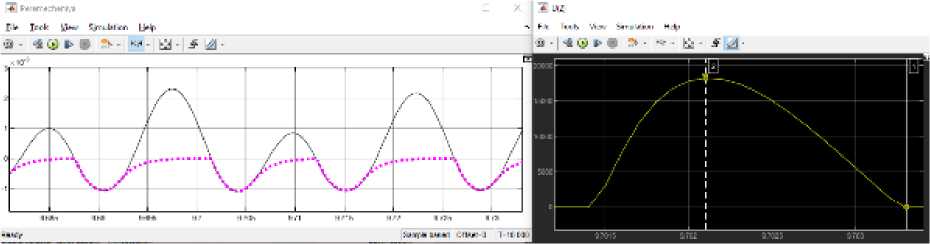
Рис. 9. Осциллограммы перемещений основания виброплиты и грунта, а также силы реакции грунта для характерного цикла нагружения ( k_s = 120 МН/м, b_s = 200 кН ⋅ с/м, m_d = 75 кг, m f = 75 кг, m_s = 15 кг, ω = 506 рад/с, P = 23378 Н, k f = 2,11 МН/м, b f = 4,17 кН ⋅ с/м, режим двойного прыжка (double jump))

Fig. 9. Oscillograms of the displacement of the of the base of the vibrating plate and the soil, as well as the soil reaction forces for a characteristic loading cycle ( k_s = 120 МN/m, b_s = 200 kN ⋅ s/m, m_d = 75 kg, m f = 75 kg, m_s = 15 kg, ω = 506 rad/s, P = 23378 N, k f = 2.11 MN/m, b f =4.17 kN ⋅ s/m (double jump))

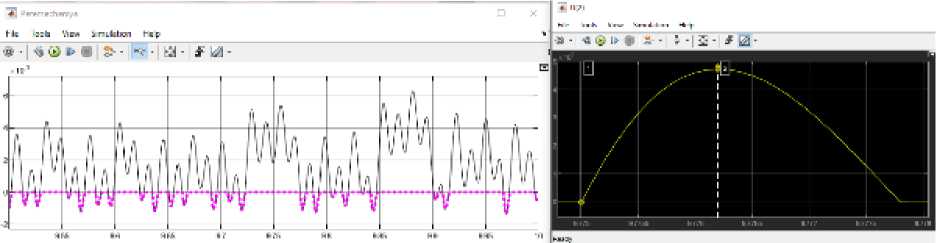
Рис. 10. Осциллограммы перемещений основания виброплиты и грунта, а также силы реакции грунта для характерного цикла нагружения ( k_s = 120 МН/м, b_s = 100 кН ⋅ с/м, m_d = 125 кг, m f = 125 кг, m_s = 25 кг, ω = 454 рад/с, P = 35651 Н, k f = 2.12 МН/м, b f = 4,67 кН ⋅ с/м, сложный режим колебаний с кратностью более 1)

Fig. 10. Oscillograms of the displacement of the of the base of the vibrating plate and the soil, as well as the soil reaction forces for a characteristic loading cycle ( k_s = 120 МN/m, b_s = 100 kN ⋅ s/m, m_d = 125 kg, m f = 125 kg, m_s = 25 kg, ω = 454 rad/s, P = 35651 N, k f = 2.10 MN/m, b f =4.67 kN ⋅ s/m (complex oscillation mode with a multiplicity of more than 1))

Таблица 2/Table 2

Регрессионные зависимости для расчета значений t 1 , t 2 и F s^max при уплотнении грунта виброплитами

Regression dependencies for calculating t 1 , t 2 и F s^max values when compacting soil with vibrating plates

№ п/п	Вид зависимости	Значение R
1	t 1 = 0,128+64,208 ⋅ m 0,76 ⋅ k s –0,259 ⋅ b s –0,285	0,94
2	t 2 = 0,78+2,92 ⋅ m 0,496 ⋅ k s –0,21 ⋅ b s 0,044	0,855
3	F s max = –2227 + 0,883 ⋅ m 0,751 · k s 0,464 ⋅ b s –0,136	0,958

На рис. 11–13 представлены некоторые графики влияния параметров m и k s на значения t 1 , t 2 и F s^max , полученные на основании обработки осциллограмм программы MATLAB Simulink и на основании регрессионных зависимостей (табл. 2).

4.    Обсуждение результатов

Анализ результатов вычислительного эксперимента показывает, что при увеличении массы виброплиты время нагружения грунта t1, время разгрузки грунта t2, а также максимальное значение силы реакции грунта Fsmax увеличиваются, что соответствуют существующим представлениям. Влияние коэффициента упругого сопротивления грунта на значения t1, t2 и Fsmax более сложное. С увеличением ks значения t1 и t2 уменьшаются, а значения Fsmax возрастают. Наблюдается также незначительное уменьшение значений t1, t2 и Fsmax при увеличении значений коэффициента упругого сопротивления грунта bs.

Характерным являются более высокие значения времени разгрузки грунта t 2 , по сравнению с временем нагружения t 1 , при всех сочетаниях исходных данных. В среднем рассчитанное по уравнениям регрессии (см. табл. 2) соотношение t 1 / t 2 составляет t 1 / t 2 = 0,63. При этом наибольшее влияние на соотношение t 1 / t 2 оказывает масса виброплиты (рис. 14).

Статистическая обработка в программе Statistica позволила получить регрессионную зависимость соотношения t1 / t2 от значений массы виброплиты m и коэффициентов упругого и вязкого сопротивления грун- та ks и bs (при R = 0,942): t1/t2 = 0,0253+40,679 ⋅ m0,678 ks–0,223 ⋅ bs–0,252.

⋅

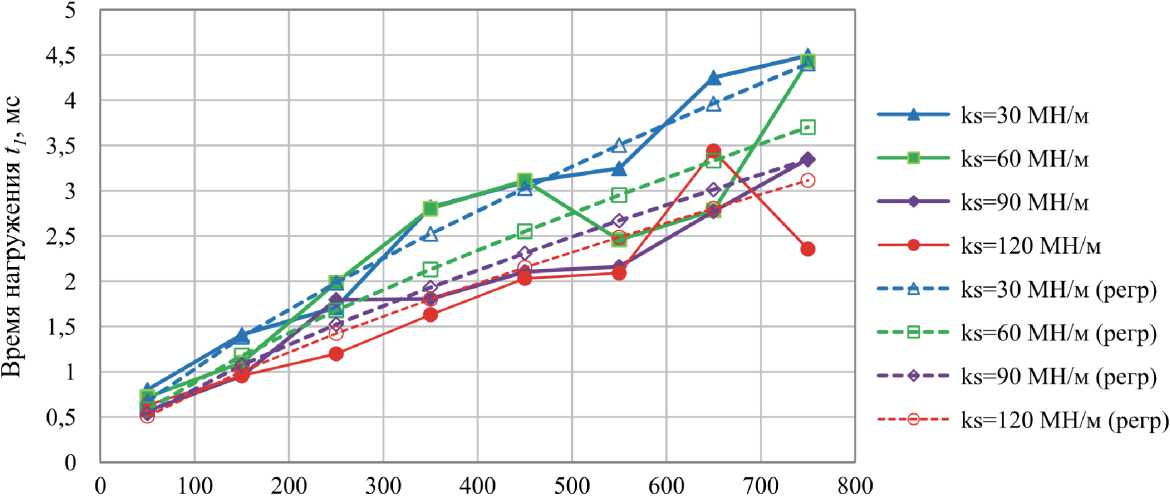
Масса виброплиты т, кг

Рис. 11. Влияние массы виброплиты m и коэффициента упругого сопротивления грунта k_s на значение времени нагружения грунта ( t₁ ) при b_s = 100 кН ⋅ с/м

Fig. 11. The influence of the mass of the vibrating plate m and the soil stiffness k s on the value of the soil loading time ( t 1 ) at b_s = 100 kN ⋅ s/m

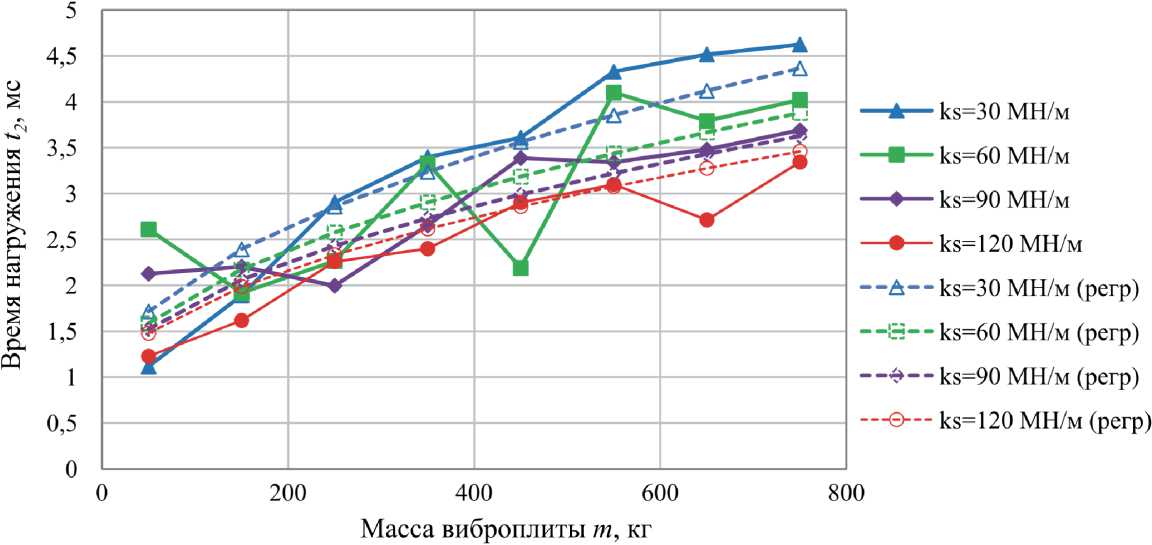
Рис. 12. Влияние массы виброплиты m и коэффициента упругого сопротивления грунта k_s на значение времени разгрузки грунта ( t₂ ) при b_s = 200 кН ⋅ с/м

Fig. 12. The influence of the mass of the vibrating plate m and the soil stiffness k_s on the value of the soil unloading time ( t₂ ) at b_s = 200 kN ⋅ s/m

1,4Е+05

1,2Е+05

1,0Е+05

8,0Е+04

6,0Е+04

4,0Е+04

2,0Е+04

0,0Е+00

—*— ks=3O МН/м

• —■— ks=60 МН/м

• ♦  ks=90 МН/м

—•— ks= 120 МН/м

• —    А— ks=30 МН/м (регр)

• — в— ks=60 МН/м (регр)

• - -❖-- ks=90 МН/м (регр)

—е— ks=120 МН/м (регр)

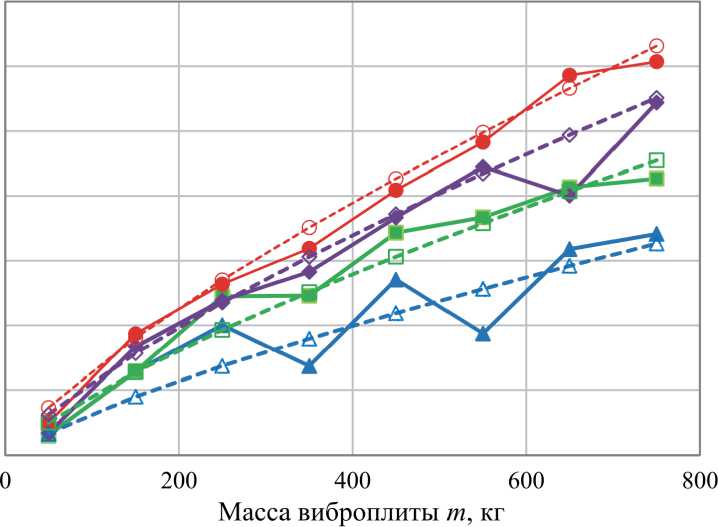
Рис. 13. Влияние массы виброплиты m и коэффициента упругого сопротивления грунта k_s на значение силы реакции грунта ( F_s^max ) при b_s = 300 кН ⋅ с/м

Fig. 13. The influence of the mass of the vibrating plate m and the soil stiffness k_s on the value of the reaction force ( F_s^max ) at b_s = 200 kN ⋅ s/m

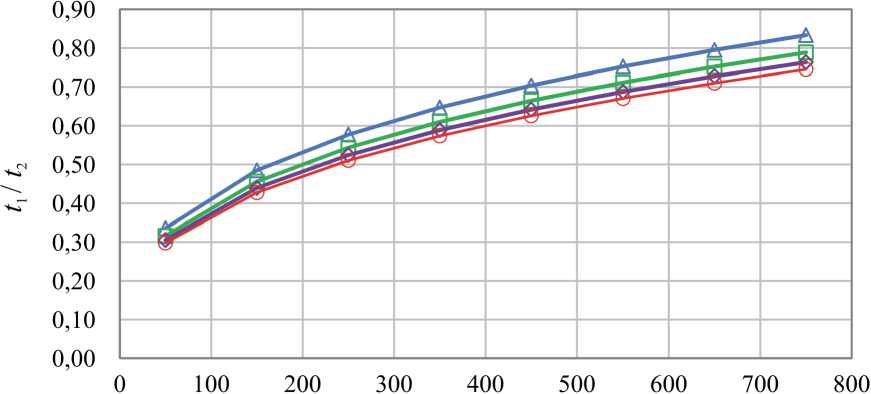
Масса виброплиты m, кг

A ks=30 МН/м (perp)

• □ ks=60 MH/м (perp)

0 ks=90 MH/м (perp)

О ks=120 MH/м (perp)

Рис. 14. Влияние массы виброплиты m и коэффициента упругого сопротивления грунта k s на соотношение t 1 / t₂ при b s = 200 кН - с/м

Fig. 14. The influence of the mass of the vibrating plate m and the soil stiffness k s on the on the ratio t 11 t₂ at b s = 200 kN - s/m

Неравенство значений времени нагружения грунта t 1 , времени разгрузки грунта t₂ (t 1 <  t₂ ) прослеживается и в результатах экспериментальных исследований уплотнения грунта виброплитами, выполнявшимися на кафедре «Строительные и дорожные машины» ЯГТУ в 2015 г. Аналогичная ситуация (t 1 <  t 2 ) наблюдается и при уплотнении грунта вибрационными катками [33] и трамбующими машинами [34].

Заключение

Определение характера изменения (амплитудное значение, продолжительность нагружения и разгрузки) силы реакции грунта на основание виброплиты позволяет определить характер изменения напряжений на поверхности контакта основания виброплиты с уплотняемым грунтом а ₀ ( t ):

ас (t) = Fs (t) /5, где S – площадь контакта основания виброплиты с уплотняемым грунтом, м2.