Моделирование взаимодействующих региональных экономических систем с использованием параллельных вычислений

Динамическую модель экономики страны, идентифицированную по данным экономики России за 7 лет [1], можно расширить для описания экономики каждого из взаимодействующих регионов и экономики страны в целом.

Модель взаимодействующих региональных экономик будет полезна при изучении проблем, связанных с переходными процессами в экономике России и её регионах. Регионы России имеют разный объём и состав природных ресурсов, обладают различным уровнем развития производительных сил, разным уровнем открытости регионов. Рассмотрение модели позволит приблизиться к пониманию причин отставания в экономическом развитии части регионов и причин успешного экономического развития другой части регионов.

В рассматриваемой экономике каждый регион производит единственный региональный продукт, который в модели имеет разную цену в разных регионах. Изменение цен в простейшей модели задается эконометрическими функциями, параметры которых отличаются в разных регионах.

Задача идентификации модели состоит в определении эффективного капитала K ( t ), такого, что рассчитанные по модели макропоказатели экономики России близки к соответствующим статистическим аналогам.

Большое количество неопределяемых напрямую из статистики параметров модели определяем косвенным образом, сравнивая выходные временные ряды переменных модели с доступными статистическими временными рядами. Временные ряды считаются похожими, если они близки как функции времени. В качестве критериев близости расчётного и статистического временных рядов используем коэффициент корреляции и индекс несовпадения Тейла.

Декомпозиция модели по регионам даёт возможность за разумное время определить независи- мые параметры благодаря параллельным вычислениям для перебора параметров модели на заданных интервалах их изменения с последовательно уменьшающимся интервалом изменения параметров.

• II.    Описание модели экономики взаимодействующих регионов

Рассмотрим модель экономики страны, состоящей из регионов, взаимодействующих друг с другом и с внешним миром. Для описания переменных моделей будем использовать индексы: i — индекс региона, N — число регионов, 0 — индекс внешнего мира, £ — индекс для страны в целом как объединения регионов.

• II.1.    Простейшая модель экономики региона

Описание простейшей модели экономики региона основано на описании простейшей модели экономики страны [1–2]. Объем валового регионального продукта (ВРП) Y i ( t ) i -го региона в момент времени t определяется удельным выпуском y i ( t ) и начальным значением ^ i = Y i (0):

Y i ( t ) = _V i y i ( t ) .                   (1)

Удельный выпуск y i ( t ) i -го региона определяется удельными производственными факторами — удельным трудом l i ( t ) и удельным эффективным капиталом k i ( t ) — в силу однородной степени Y i производственной функции с постоянной эластичностью замещения (CES):

y i ( t ) = [ a i ( l i ( t )) ^{- e} i + (1 - a i ) ( k i ( t )) ^{- e} i ] ^{- Y i /e} i .

(2) Параметры в соотношении (2) удовлетворяют ограничениям: a i E (0 , 1), P i > — 1, Y i ^ 1.

Удельный труд в i -м регионе меняется экспоненциально с темпом λ i :

l i ( t ) = exp ( X i t )

и определяет численность занятых в экономике для i -го региона (труд) L i ( t ):

Li (t) = ^i li (t) , где ^i = Li (0) — начальное значение числа занятых в i-м регионе.

Динамика удельного эффективного капитала ki (t) в i-м регионе определяется задачей Коши:

^i = —^iki (t) + ni^iyi^TT,, ki (0) = 1, dt                         pi (t)

где — ^ i — темп изменения существующего капитала, 9 i >  0 — коэффициент пропорциональности объёма региональных инвестиций объёму ВРП:

ⁿ i    K i (0)

ϕ i

K i (0)

> 0 .

Индекс цен на инвестиции определяется эконометрической функцией

P i ( t ) = ^ i + (1 — ^ i ) (1 + t ) exp ( —w i t )

с двумя параметрами ^ i E (0 , 1) и ш _i >  0.

Объем инвестиций в i -м регионе определяется соотношением

J i ( t ) =

d i ^ i V i ( t ) P i ( t )

Объемы вывоза из i -го региона в j -й определяются соотношениями

E ij ⁽ t ) =

V i V i ( t ) 5 ij r ij ⁽ t )

где δ ij — норма вывоза выпуска из i -го региона в j -й при j = 1 , ..., N или доля экспорта в выпуске при j = 0, r ij ( t ) — индекс относительной цены на вывозимую продукцию из i -го региона в j -й при j = 1 , ..., N или индекс относительной цены на экспорт при j = 0:

rij (t) = Kij + (1 — Kij) exp (—nj t) , каждый из которых определяется двумя параметрами: Kij E (0,1) и nij.

Объемы ввоза из j -го региона в i -й определяются соотношениями

N

E M — ( t ) , m =0       s ^ji

I ji ⁽ t ) = V i V i ⁽ t ) f

где ρ ji — норма отношения объёма ввозимой из j -го региона в i -й регион к продукции i -го региона, реализуемой на внутреннем рынке (при j = 0 норма отношения импорта к объёму собственной продукции, реализуемой у себя), s ji ( t ) — индекс относительной цены на ввозимую продукцию из j -го региона в i -й при j = 1 , ..., N или индекс относительной цены на импорт при j = 0:

sji (t) = 1 — Zjit2 exp (—Vjit), каждый из которых определяется двумя параметрами: Zji > 0 и Vji > 0.

Объемы потребления домашних хозяйств, правительственных и общественных организаций, выраженные в единицах валового регионального продукта в постоянных ценах 2000 года ( t = 0), определяются из основного макроэкономического баланса i -го региона:

Q i ( t ) = Y i ( t ) — p i ( t ) J i ( t ) +

NN

+ E s ji ( t ) I ji ( t ) — E r ij ( t ) E ij ( t ) .     (3)

j=0                j=0

Уравнения (1)–(3) полностью описывают модель экономики региона.

• II.2.    Замыкание модели взаимодействующих регионов

Кроме указанных выше параметров каждый регион характеризуется дефлятором ВРП x i ( t ), который связан с дефлятором валового внутреннего продукта (ВВП) x в ( t ) следующим соотношением:

N x в (t) Yв (t) = Exi (t) Yi (t).

i=1

Объединение объёмов инвестиций в регионах даёт суммарный объём инвестиций страны:

N x в (t) p в (t) Jв (t) = E xi (t) Pi (t) Ji (t).

i=1

Внутренние поставки из региона в регион согласованы, в пути ничего не теряется: в i -й регион из j -го ввозится ровно столько, сколько из j -го региона в i -й вывозится:

xi(t) sji(t) Iji (t) = xj (t) rji(t) Eji(t), i,j E {1, ..., N} .

Таким образом, суммарное сальдо внутренних поставок по всем регионам SI ( t ) равно нулю:

SI ( t ) =

N / N\

= E xi (t) I E (rij (t) Eij (t) — sji (t) Iji (t)) ) = 0, i=1

а внутренний товарооборот TI ( t ) равен удвоенному объёму суммарных поставок:

NN

TI (t) = E xi (t) E (rij (t) Eij (t) + sji (t) Iji (t)) = i=1

NN

= 2E E x i ( t ) r ij ( t ) E ij ( t ) = i =1 j =1

NN

= 2E E x i ( t ) s ji ( t ) I ji ( t ) .

i=1 j=1

Сальдо внешней торговли страны и регионов в рублях текущего года:

N

SO s ( t ) = £ SO i ( t ) , i =1

SO i ( t ) = X i ( t ) ( r i 0 ( t ) E i 0 ( t ) - s 0 i ( t ) 1 0 i ( t)).

Внешнеторговый оборот страны и регионов в рублях текущего года:

N

TO s ( t ) = ^TO i ( t ) , i =1

TO i ( t ) = X i ( t ) ( r i 0 ( t ) E i 0 ( t ) + s 0 i ( t ) 1 0 i ( t)).

Уровень открытости экономики страны O s ( t ) можно определить как отношение суммы внутреннего межрегионального и внешнего товарооборота к ВВП:

O s ( t ) =

TI ( t ) + TO s ( t ) x s ( t ) Y s ( t )

Уровень экономической безопасности страны можно определить как долю внутреннего межрегионального товарооборота к суммарному товарообороту:

Уровень этих показателей зависит от того, как много регионов рассматривать.

• III.    Параллельные вычисления для идентификации модели взаимодействующих регионов

Для страны в целом действуют уравнения (1)–(3) с индексом вместо i и отсутствием межрегиональных потоков.

Заметим, что все параметры и начальные значения (и варьируемые, и фиксированные) обозначены малыми греческими буквами, а интенсивные и относительные переменные — малыми латинскими. Время t таково, что t = 0 соответствует 2000 году.

На основе статистических данных по экономике России 2000-2006 гг. и балансовых соотношений модели взаимодействующих регионов подготовлены исходные данные для двухрегиональной версии модели взаимодействующих регионов России.

Статистические данные для страны в целом представлены в табл. 1 [1, 3].

B s ( t ) =

TI ( t )

TI ( t )+ TO s ( t ) .

Таблица 1

Статистические данные РФ

год	2000	2001	2002	2003	2004	2005	2006	2007
L P	65,273	65,124	66,266	67,152	67,134	68,603	69,157	70,813
r P	1,000	0,844	0,766	0,729	0,685	0,697	0,670	0,670
s P	1,000	0,892	0,823	0,731	0,592	0,522	0,456	0,440
p P	1,000	1,008	0,992	0,960	0,921	0,878	0,852	0,868
Y P	7305,600	7676,900	8025,417	8618,443	9237,806	9830,616	10570,415	11462,846
I P	1755,800	2084,100	2388,400	2811,200	3466,200	4055,400	4878,700	5655,840
J P	1165,200	1281,757	1317,647	1482,352	1685,435	1869,147	2181,295	2641,548
E P	3218,900	3354,100	3699,600	4162,000	4653,100	4950,900	5297,500	5188,857
Q P	4677,300	5412,133	5850,223	6217,321	6550,991	6857,338	7384,669	8180,904
x P	1,000	1,165	1,348	1,537	1,845	2,200	2,545	2,889

Источник: Федеральное агентство по статистике

Мы предполагаем, что

• —    первый регион (метрополия) взаимодействует с внешним миром и со вторым регионом;

• —    второй регион (провинция) взаимодействует только с первым регионом.

Формируем данные для первого региона (табл. 2) на основе следующих допущений.

• 1.    Численность занятых в экономике первого региона составляет половину от занятых в стране:

L ^P

• L ¹       2 .

• 2.    Индексы цен на экспорт, импорт и инвестиции в первом регионе r 1 i , s i 1 ( i = 0 , 2) и p 1 такие же, как у страны.

• 3.    ВРП первого региона равняется половине от ВВП: Y 1 = Y P .

• 4.    Объем инвестиций первого региона равен половине объёма инвестиций в основные фонды страны: J 1 = J p .

• 5.    Объем вывоза продукции из первого региона во второй равен четверти экспорта: E 12 = E 10 • 0 , 25.

• 6.    Объем ввоза из второго региона в первый равен половине импорта: 1 ₂₁ = I 2 1 .

• 7.    Дефлятор ВРП первого региона x 1 задан произвольными данными (для примера взяты значения дефлятора ВРП Кировской области).

• 8.    Объем потребления в ценах ВРП 2000 г. Q 1 вычисляется по балансовому уравнению (3).

Данные первого региона представлены в табл. 2.

Таблица 2

Данные первого региона РФ
год 2000      2001      2002      2003      2004      2005      2006      2007
L 1   32,637    32,562    33,133    33,576    33,567    34,302    34,579    35,407
r 12   1,000      0,844      0,766      0,729      0,685      0,697      0,670      0,670
s 21   1,000      0,892      0,823      0,731      0,592      0,522      0,456      0,440
p 1    1,000      1,008      0,992      0,960      0,921      0,878      0,852      0,868
Y 1    3652,800  3838,450  4012,709  4309,221  4618,903  4915,308  5285,207  5731,423
I 01   1755,800 2084,100 2388,400 2811,200 3466,200 4055,400 4878,700 5655,840
J 1    291,300   320,439   329,412   370,588   421,359   467,287   545,324   660,387
E 10  3218,900 3354,100 3699,600 4162,000 4653,100 4950,900 5297,500 5188,857
E 12  804,725   838,525   924,900   1040,500 1163,275 1237,725 1324,375 1297,214
I 21   877,900   1042,050 1194,200 1405,600 1733,100 2027,700 2439,350 2827,920
Q 1   1971,575  2763,865 3092,877 3244,238 3325,804 3369,431 3717,092 4545,115
x 1    1,000      1,160      1,420      1,620      1,850      2,080      2,280      2,410
Для формирования данных второго региона        индекс цен на продукцию, вывозимую из вто-
делаем дополнительные предположения:              рого региона в первый r 21 , отличается от r 12 ;
индексы цен на ввозимую продукцию и		инве-
во	втором регионе общий уровень роста цен     стиции s 12 и p 2 такие же, как у страны.
больше, чем в первом регионе и в целом по стране:        Данные второго региона представлены в
x 2 >x P >x 1 ;                                       табл. 3.
Таблица 3
Данные второго региона РФ
	год 2000      2001      2002      2003      2004      2005      2006      2007
	L 2   32,637    32,562    33,133    33,576    33,567    34,302    34,579    35,407
	r 21   1,000      0,920      0,890      0,760      0,620      0,550      0,470      0,470
	s 12   1,000      0,844      0,766      0,729      0,685      0,697      0,670      0,670
	p 2    1,000      1,008      0,992      0,960      0,921      0,878      0,852      0,868
	Y 2    3652,800  3805,921  3435,875  3640,850  4294,510  5000,684  5604,991  6542,634
	I 12   804,725   824,313   881,448   980,006   1086,898  1129,153  1139,462  1059,758
	J 2    873,900   950,456   878,052   975,260   1177,226  1377,103  1625,822  2047,215
	E 21  877,900   993,256   1052,918 1272,927 1546,076 1755,423 2034,280 2162,803
	x 2    1,000      1,180      1,490      1,720      1,980      2,280      2,650      2,950
	Q 2   2705,725  2630,439  2302,754  2451,375  2995,852 3612,239 4027,257 4458,308

Параметры a i , ^ i , Y i , P i , n i ( i = 1 , •••, N, ^) варьируются.

Задача идентификации модели состоит в определении эффективного капитала K ( t ), такого, что рассчитанные по модели макропоказатели экономики России близки к соответствующим статистическим аналогам. В частности, для экономики России в целом справедливы такие оценки [1]: показатели индекса цен на инвестиции в рассматриваемый период £ в = 0 , 811, ш в = 0 , 5276; темп роста труда А в = 0 , 01124; отношение начального выпуска к начальному капиталу находится из интервала n в € [0 , 05 , 2]; темп падения капитала в силу естественных причин находим из интервала ц в € [ — 0 , 2 , 0 , 20]; искомые параметры производственной функции находим из условий а в € (0 , 1), в в > — 1, Y в >  1.

Предположим отсутствие научно-технического прогресса, что в модели представлено линейной однородной производственной функцией с y в = 1.

При каждом заданном наборе фиксированных и варьируемых параметров можно найти реше- ние модели. В результате найдём относительный эффективный капитал к в (t) и относительный выпуск ув(t). Валовой внутренний продукт (ВВП) в ценах 2000 г. Y(t) определяется начальным значением ВВП: ув = Yв(0) = 7305,6. Значение параметра ηΣ определяет начальный уровень эффективного капитала в 2000 г.: Kв(0) = ^. Эффективный капитал определяется формулой

K в( t ) = к в( t ) fracy в П в •

Труд определяется фиксированными параметрами, определёнными подгонкой экспоненциальной функции к статистическим данным: расчётным начальным значением L в(0) = ^ в = 64 , 84 и оценкой темпа роста λ Σ :

L в( t ) = ^ в e ^{X Е} t .

Инвестиции в основной капитал определяются относительным выпуском ув(t) и фиксированными параметрами, включая параметры, определяющие относительный индекс цен на инвестиции p в( t):

J в ⁽ t ) = ⁹ в V в У ⁵ (,) • p в ⁽ t )

Относительный индекс цен на экспорт определяется фиксированными параметрами — асимптотой к = 0 , 6684 и темпом падения п в = 0 , 6142:

r в ( t ) = к в + (1 - к в) e ^{п в} t

d2 + = pow (x [p], 2);

d3 + = pow (y [p], 2);

} return 1 •0 — sq^t ((55+53)) ;

}

При завершении расчёта каждый процесс, отличный от нулевого, посылает нулевому процессу результаты своих расчётов, своё локальное луч-

и вместе с фиксированными параметрами и относительным выпуском у в( t ) определяет объём экспорта:

E в( t ) = 5 в V в У в ( t ) /г в( t ) •

Относительный индекс цен на импорт s в( t ) определяется фиксированными параметрами — Z в = 0 , 0712 и V в = 0 , 2602:

s в( t ) = 1 - Z в t ² ' '"^в t

и вместе с фиксированными параметрами и относительным выпуском У в ( t ) определяет объём им-

порта:

I в ⁽ t ) = Р в ^{(1 — 5} в) V в У ^в (2 • s в( t )

Объем конечного потребления домашних хозяйств, правительственных и общественных организаций страны определяется соотношением

Q в( t ) = Y в ( t )+ s в( t ) I в ( t ) —p в( t ) J в( t ) —r в( t ) E в( t ) •

Параллельные вычисления реализованы с использованием технологии MPI на языке C++.

Каждый из 5-ти параметров может изменяться задаваемое количество раз в определённом диапазоне.

Для удобства параллелизации процесса перебора параметров вместо пяти циклов будем работать с одним. При каждой итерации этого общего цикла рассчитываются индексы виртуальных циклов при помощи специальной процедуры.

В качестве критериев близости расчётного и статистического временных рядов используем коэффициент близости U ( X, Y ) = 1 — E ( X, Y ), где E ( X, Y ) — индекс Тейла.

Чем выше U ( X, Y ) (чем ближе к единице), тем более близки ряды:

U ( X, Y ) = 1 —

Е T = 1 0 ( X t — Y t ) ²

e t= t о Xt2+e:

T Y ₂ • ' t = t 0    t

шее решение.

Нулевой процесс в свою очередь принимает от остальных процессов решения и выбирает из них наилучшее, отображая его на экран.

Результаты расчётов для первого региона: лучшее значение коэффициента близости:

F = 0 , 997008025646;

параметры: {0,767677; — 0 , 939394; 1,000000;

— 0 , 175758; 0,089394};

ВРП Y :    {3652,800049;    3841,393311;

4056,659912; 4303,503906; 4587,449707; 4914,886230; 5293,271973; 5731,354980};

удельный капитал k : {1,000000; 1,183982; 1,400469; 1,655696; 1,956731; 2,311776; 2,730428; 3,223964}.

Результаты расчётов для второго региона: лучшее значение коэффициента близости:

F = 0 , 942227363586;

параметры: {0,939394; — 1 , 000000; 1,000000;

— 0 , 200000; 1,803030};

ВРП Y :    {3652,800049;    3845,475098;

4071,422363; 4344,256348; 4677,159180; 5084,835938; 5584,666016; 6197,772461};

удельный капитал k : {1,000000; 1,687916; 2,523975; 3,569652; 4,884473; 6,534826; 8,599195; 11,172968}.

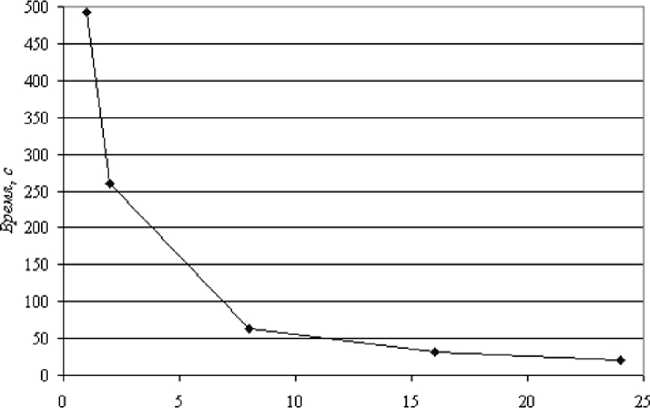
Было сделано несколько запусков программы на разном количестве процессоров [4, 5]. На рис. 1 приведены графики зависимости времени расчёта от числа процессоров при общем числе итераций 100 млн, а на рис. 2 показано ускорение вычислительного процесса в зависимости от числа процессоров.

Таким образом, очевидна идеальная паралле-лизация данной задачи за счёт отсутствия межпроцессорных коммуникаций.

Получен работоспособный вариант параметров модели. Расчёты производились на суперкомпьютере Вятского государственного университета HP HPC Enigma X000 «Татьяна».

IV. Заключение

Расчёт коэффициента близости (4) производится при помощи функции bliz ():

float bliz (float *x, float *y, int n) { float d 1 = 0. 0, d 2 = 0. 0, d 3 = 0. 0;

for (int p = 0; p < n; p+—+) { d1 + = pow (x [p] — y [p], 2);

В работе использована технология идентификации внешних параметров модели, базирующаяся на высокоскоростных параллельных вычислениях на многопроцессорных системах, параметры экономики каждого региона рассчитывались параллельно.

100 млн итераций

процессоры

Рис. 1. Зависимость времени расчёта от числа процессоров

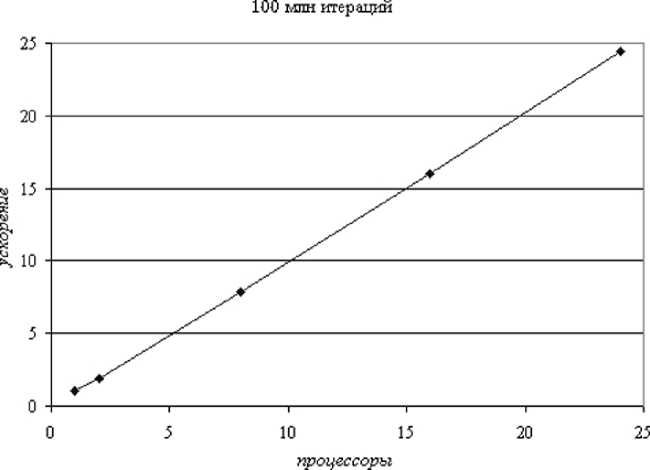
Рис. 2. Ускорение вычислительного процесса в зависимости от числа процессоров