Моделирование задачи о свободном растекании пластического слоя, состоящего из разных сред, в постановке модели "идеальной жидкости"

EDN: RGOMXP

ПОСТАНОВКА И РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ

Краевая задача течения тонкого слоя по плоским шероховатым поверхностям ставится следующим образом. Рассматриваем пластический слой в клиновидной области, составленный из материалов с разными механическими характеристиками. Положение прямолинейных границ, пересекающихся в начале выбранной неподвижной прямоугольной системы координат Оху, задается начальными углами «₁ и «₂ соответственно (рис. 1). Предположим, что такой слой свободно растекается между параллельно сближающимися жесткими шероховатыми плитами. Слой под действием в направлении толщины распределенной нагрузки со стороны инструмента беспрепятственно течет в направлении радиусов. Подобная задача при условии симметричности пластической области в постановке математической модели «идеальной жидкости» решена в [5].

Выберем неподвижную систему координат Оху, в которой в начальный момент времени t _ t_o указанная область задается углом р₂ > 0. При этом сами линейные границы растекающейся области в начальный момент заданы уравнениями прямых:

Г^у _ к₁х,; к₁ > 0,

Г2:у _ к2х; к2 < 0,

Г12:у = кох, где к1,к2,ко - коэффициенты определяются через известные углы «1, а2 и р2:

tgP 2 =-к г ;

tg(« 2 -P2) = к о ;

tgV« i + (« 2 -P 2 )] = к 1 .

Система дифференциальных уравнений в частных производных краевой задачи течения пластического слоя на плоскости (в размерных величинах, t > t0) состоит из двух уравнений квазистатического равновесия относительно неизвестного давления p на контакте (1) и (2) и условия несжимаемости (3):

Эр _ _- 2r_st _     и .

Эх      h i Уи² + v^{z ;}

Эр _ _- ^2т $к .     и _;

^{Эу     h}i Уи² + v ²

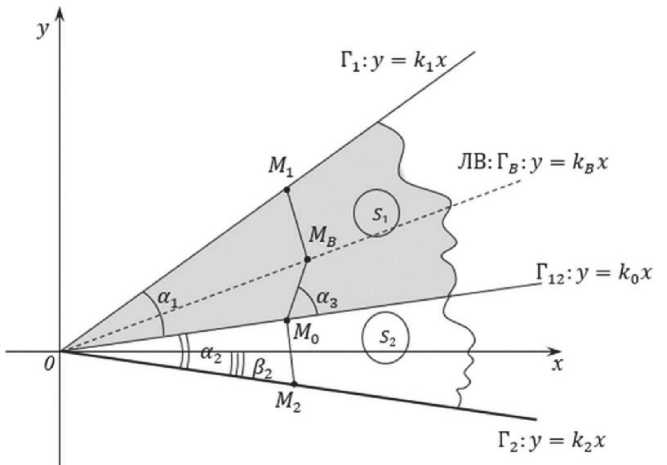
Рисунок 1. Схема пластической области в форме клина из материалов с разными механическими характеристиками:

М ₀, М ₁, М ₂ – точки, принадлежащие линейным границам;

S ₁, S ₂ – области, занимаемые двумя различными по свойствам материалами

ди । д: дЛ _ о дх ду dt "

Дополняет систему неизвестная граница раздела двух сред

Wy _ Ф о ⁽хЛ); t > t o ⁾, которая в начальный момент задана уравнением

Ф о ⁽х,t о ⁾ _ к о х;

на этой границе давление выравнивается

Р 1 = р₂; дф о , _цдф о _ ^ dt дх "

На неизвестных свободных границах

Г_т(У = Ф т ⁽х, t⁾,t>t о ,m_ 1,2 ), которые в начальный момент также известны

(^ m (x,t o ) = к т х):р _ 0;

дфт ! и дфт г dt дх , здесь и, и-скорости течения;

Osk _ V3tsk (к _ 1,2) - предел текучести пластического материала в областях 01 и S2 соответственно, причем для определенности положим, что os1 < os2;h _ h(t) - известный закон изменения толщины слоя; A(t) _ In (j^ - степень деформации; hо _ h(tо) - толщина слоя в начальный момент времени tо.

Примем за Ь_о - характерное значение линейного размера слоя. Введем безразмерные величины:

_ h £_ U

• о

- о

Обезразмерим величины в уравнениях задачи:

/ dh(t о ) \

;₅_^: ¹ ;р о _^: ¹ ;^ о _А^и,. a_S 2          Е                Е

"

др _ дх ""

др _ ду

5 ^д р _ дх

5 ^д Р _ ду

2 1 и ^Ф^;

L1 ^и

BS1;

2 1 и

^{2 1 и}

-р = —р , B 07;

|^ + |^ -^=0, BSiUS^                                   (8) Эх Эу at     ,      1     2 Р1 = Р2;                                                                      (9) 5 + U5 = v на^;                             (10) p = 0;                                                                (11) ^ + U—=v   на Г (к = 1,2).                        (12) Эt        Эх       ,            k 4        ,

Задача решается в безразмерных величинах. Для удобства записи диакритические знаки в виде черты над безразмерными величинами в дальнейших рассуждениях опускаем. Как известно [1], внутри области течения существует линия раздела течения, образованная пересечением двух различных линий тока, и на которой u ² + v ² = 0. С другой стороны, при h = h(x) линиями тока служат прямые, ортогональные к контуру свободно растекающегося пластического слоя. Пусть М₀(х₀;у₀) некоторая точка на линии раздела двух сред Г₁₂ (см. рис.1). Для определенности положим, что:

yS i sin«1 > yS 2 sin«2.                                                     (13)

Предположение (13) означает, что линия раздела течения в начальный момент времени t = t₀ располагается в области S₁. Поэтому продолжим линию тока, исходящую из области S₂, в область S₁, отсчитывая от точки М₀ е Г₁₂. Для этого найдем угол преломления 2 - а₃ линии тока в точке М₀ [5]:

dp(s) . = ds = g£+££.         х 2 3х ds 3yds V3h5   ^2    / V3h 5cosa3 = sina2,                                                      (14) где s - параметр длины дуги вдоль линии Г12. Формула (14) означает, что при пересечении линии раздела двух пластических сред линия тока преломляется, причем угол преломления увеличивается при прохождении в «менее плотную» среду (аналогия с оптикой). Из (14) следует, что все линии тока входят в область S2 под постоянным углом к оси Ох. Теперь, определив линию тока, исходящую из точки М0 е Г12, можем найти на ней точку Мв(хв;ув) ветвления течения из следующего условия:

\. ^ОМ ".■■ ' ₂ ^М V :      ■/ '+ '.                                   (15)

В (15) справа стоит выражение для контактного давления в точке М_в, найденного вдоль другой линии тока, исходящей от контура Г₁ , причем величина:

|кххв-ув1   к1Хв-ув s       П.----Tn        R----Tn , V1 + к1     V1 + к1 есть расстояние от точки Мв до границы ГР Находим оставшиеся в (15) величины:

ОМ 0 = V x 2 + y 2 = X 0 J1 + к 0

Уравнение прямой М0Мв:

У - У0 = tg(^0 + «з) ' (х - Х0),                                         (16) где 0 = arctgko > 0.

Из (13) получаем:	tg^ 0 +tga 3     k o sma 2 +Va2-sm2a 2 к 5    tg( ^ 0 + « з ) = 1-tg, 0 tg1 Z 3 = siM 2 - k o Va r -^                      (17)
С другой стороны:	t g ( « 2 - М + t g 0 2     к 0 - к 2 tg« 2 = tg[ ( « 2    AD + 0 2] = , _z      р х_р = , , , , ; 1 - tg ( « 2 - P2)tg02   1 + к 0 к 2 sina2 = / ts2 “ 2 = .     ko - k 2 = > 0.                           (18) 2   ^1+t S 2a 2    V(1+k o k 2 )2+(k o -k 2 )2

Подставим (18) в (17) и найдем к5 в зависимости от к0,к2 и 5:

к = fc o C^ Q -^ 2 )^V£2(1^^ 0 ^ 2 )2^£2(^ 0 —^ 2 ) ^                                          (19) 5    (k 0 -k 2 )-k 0 V 52(1 + k o k 2 )2 + ^2(k o -k 2 )2

В частности, при 5 = 1 (т.е. пластическая среда - однородная) из (2.80) и (2.77) соответственно

получаем:

1 к 5 = -к?              _____ М 0 М в = V ( У в - У 0 ) 2 + ( х в - Х 0 ) 2 = | х в - X q V + к; 2 ,                      (20)

Подставим (18), (19), (20) в (15):

/l(ki,k2,ko,a) хв = х0 с rv V V XV                                                      (21) /2(kl'k2'k0'^.) где л = —1 77^™,+17771+1^—k^ ——1, Vт:+'?о(kо-kl—+ KTll+j^z^-, 5^     °              5 VT+kl    5V(1 + k0ki)l + (k0 — ki)1         5 Vт + kT

^Virk f — .

J1+kt

Как видно из (20), (21), линия ветвления (ЛВ) в момент t — t ° есть прямая:

_ ^f l ^k 5 + / 2 (^k Q ^-k s )

■

У в — k_Bx_B,k_B

ft

В частности, при 5—1 формула (22) упрощается:

k _— ^k z V ¹ + ^k l + ^k l V ¹ + ^k 2

^B V1 + k l +V1 + k l ^,

1 , arctgk_B — arctgk₁ — arctgk₁ — arctgk_B — - (arctgk₁ — arctgk₁).

Последняя формула означает, что для однородного пластического слоя линия ветвления равно отстоит от линий свободных контуров Г1 и Г1. Если дополнительно принять, что k1 — —kl, то получаем: кв — О, т.е. линия ветвления совпадает с осью Ох. Получим теперь зависимости для контактного давления и скорости течения в начальный момент. Рассмотрим сначала область S1B, ограниченную линиями Г1 и Гв. Линия тока, проходящая через точку М(х,у) е S1B:

У — У в — —-"Jx — Xb)

Последнее условие разрешается относительно хв k1y + х в —1—в + 1

Тогда,

V ⁽ x,y ⁾ — ‘Ах в dt

^j ¹⁷ —¹ dt

- ⁽ k 1 X — y) Р ⁽ х,У ⁾ — n, I----74 , y3h V1 + — 1

dA (х_в

— x)V 1 + — 1     dA V1 + — 1

и — Vcos (^ — д ! \ — —VsinP 1 — — ^Vk1

^{v -    1}               V1 + — 1

ki dA

’ ^{— —} di ^(X B

dt k₁k_B + 1

⁽ У — — в х),

dAk 1 (y — — в х)

— Х) —--:--—------- , dt k₁k_B + 1

v — Vsin ( ^ — p₁^ — Vcosp₁ —

V   _ dA(xB~x) _ dAki(y-kBx)

1 _+k i   at ki      dt kik_B^1

где p₁ — arctgk₁ > О .

Рассмотрим теперь область S_B0 , ограниченную линиями Г_в и Г₁₁ . Линия тока, проходящая через точку

М(х, y) е S_B0 , имеет вид:

y — Ув — — 5 ⁽ х — х_ь).

Разрешим последнее уравнение относительно х_в:

Х в

y — — 5 X ^k B ^{— k} 5

Тогда,

с \        х ^{-              - (—}1^Хв ^yB⁾ ,   ^- г, -------УГГЛ-------У?

p ⁽ x,y ⁾ — р ⁽ М в ⁾ + ^=h ⁽ М в М ⁾ — ^-_h j£+— r + V5h ^V( y — У в ⁾¹ + ⁽ х — Х в)¹ —

= - У — к₅х \ (к_г — k_B)   - У-1вх \ I ₁

^3hVk B — — 5 ) JT+k₁₁   V3hVk B — k5,H     ^{5 ,}

V ⁽ Х, y ⁾ —d ^{A (} М в М) — ‘dt ^V(X b — x) ¹ + ⁽ У в — y ^{) 1} — ^dA |х — Х в |J1 + k ¹ — — ^ ⁽ Х в — х ⁾ ^1 + k ¹ —

U —

, x V

—Vcos ⁽ a₃ + p°) — —

Vт + kI

— — ^d^ Vт+"k 1 ( ^-^k в ^x ), dt^       ⁵ kB-k_s)

v —

—Vsin(a₃ + Д ° ) — —

V ■ tg ⁽ a₃ + p°) V1 + tg^{1 (} a₃ + p°)

dA           dAy — квх dt Хв Х      dt kB — k5'

dA               dA ⁽ y —— в Х ⁾ — 5

^—   dt ^{(x B Х})^{— 5 —} dt k_B—k₅

Рассмотрим, наконец, область S_B1 , ограниченную линиями Г₁₁ и Г₁ . Линия тока, проходящая через

точку М(х,у) е S_B1 , имеет вид:

У — У о ——7 ⁽ х — Х о) .

Разрешим последнее условие относительно х ° :

х °

— 1 У + х

— 1 к ° + 1.

Тогда, 2 |к 2 хв у|    2 у-к₂х

Р ⁽ х,у ⁾ = —--,     „ = -=--,     „.

V3h5 ТГ+к ² V3h5^TTk I

Согласно (14) и (18),

1 + к о к 2

sina ₃ = 71 в cos²a₃ = ^1

cosa₂ =       — =

71 + tg ² a 2 ^(1Tk о к₂У + (к о -к₂)²

^^^^^^в

1_sin2a      у^СМк,^) ² I (5 ² 1)(кГкФ

^{5 2 Sm} “²         57(1 + W² + (к , к ₂ ) ^{2 ,}

В результате,

ах /      ;к₀

^V(M о2 ⁾ = а^4 ^{1 + к 2} к ;

^{в к} в ^{75 2 (1 + к} 0 ^к2^ ^{2 + (5 2 в}

^^^^^^в

^к 5

5(к ₀ к ₂ + 1)

1)(к о вк 2 ) ² ----------------^х0,

V(x,y) = V(M 02 ) + ^аХ (М 0 М) = V(M 02 ) + ^аX 7(x-X о ) ² + (y-У о ) ² = at                   at

ах

= V( ^M 02 )+^^(X 0

Ф-

^^^^^^в

71 + к 2 ² к

ах а<ф" у

^-^^[^ - ^^^^(у K 2 K Q T1

^^^^^^в

^ф 1 = J ^{1 + к} 2

^к 0 ^к в

^^^^^^в

к в 75 ² (1 + к 0 к 2 )^+(5 ²

^^^^^^в

^^^^^^^

^к 5

5(к о к 2 + 1)

1)(к₀-к₂) ²

^{0   2J} ^у + х),

и(х,у) = —V(M)cos ^2 в ^ г ) = —V(M')sinp₂ =

ах ф ■ к ₂ ^at 71 + к

V ⁽ x,y ⁾ = -V ⁽ M)sin^ | -P 2 ) = -V ⁽ M)cosP 2 = в

ах

. 2

^ 2

^dt /1+к²

Итак, нашли распределение p,u,v во всей области течения в начальный момент. Покажем, что

линии Г₁,Г₂,Г₁₂ остаются прямыми. Допустим, что они остаются прямыми, то есть их можно задать

уравнениями:

Г 1 :у = к 1 ⁽ t ⁾ x

Г > :у = к 2 ⁽ t ⁾ x

Г 12 :у = к о ⁽ t ⁾ x

Подставим (27) в кинематические условия (12):

ахк ₁ (увк _в х) ах к ₁ вк _в

Д: к1х ка at к1кв + 1     at к1кв + 1, в которой использованы формулы (24) относительно скоростей, а у = к1х, или:

^Г 1 ^{: к} 1

—

ахк ₁ ² (к ₁ в к _в ) ахк ₁ в к _в

Г 1 :

at к 1 к в + 1     at к 1 к в + 1

dk i     (к 1 -к в )( ¹ +к 1 ²)

---= ----------------.

ах

kikB+1

Аналогично получаем дифференциальное уравнение относительно Г ₂ :

^Г 2 ^{: к} 2 ^{х + к} 2

ах ф ■ к ₂

ах ф

^at 71 + к ₂ ^{2      at} 71 + к ₂ ²

где ф определяется из (26), в которой у = к ₂ х:

Ф ⁽ х ⁾ = ф 0 х,

^{Ф 0}    к ₂ к ₀ + 1

^ ^ф 2 ^в J ^{1 + к} 2 ^(к 2 ^{в к} 0 ⁾ j ^,

или

^ф 2 ⁼ ^ ^{1+к 2 к} ;

^{в к} в ^{75 2 (1 + к} 0 ^к 2 ^{) 2 + (5 2 в}

^^^^^^в

^к 5

5(к 2 к 0 + 1)

1)(к₀—к₂) ²

^{0 2} (1 + к 2 ² )

Г 2 : аах² = —ф о 71 + к 2 ²

В частности, при 5=1 и к ₂ = вк ₁ формулы (29) и (30) упрощаются:

Г 1 : ^ак 1 =к 1 (1 + к ² ), ах             _____

Г -: ^ = к 2 (1 +к 2 ² ),ф 0 = вк 2 /1 + к 2 ² , ах

т.е. получили известное дифференциальное уравнение задачи о растекании однородного пластического слоя, занимающей область формы клина.

И, наконец, третье дифференциальное уравнение (2.71) относительно Г ₁₂:

^Г 12 ^:к 0 ^х

^^^^^^в

^к 0

ах у в к _в х ах (у в к _в х)к ₅

at к _в в к ₅    at к _в

^^^^^^в

к ₅ ^,

где использованы формулы (2.117) для скоростей, в которых у _ k_ox. Или

^ .dk g _ (^k o - ^k s )(^k o ^{— k} s ) dA         k g — k s

Система нелинейных дифференциальных уравнений первого порядка (1), (2), (3) в общем случае решается численными методами. В результате получаем законы изменения границ пластических областей в процессе растекания.

Таким образом, представлено в полном виде точное решение несимметричной задачи о растекании пластического слоя, составленного из двух клиньев, в математической модели «идеальной жидкости», причем:

Показано, что границы этих клиньев остаются прямыми в процессе растекания.

Выведены уравнения для эволюции их границ.

Установлено, что линия ветвления течения остается прямой в процессе растека

ния. Выведены формулы для нахождения линии ветвления течения.