Моделирование закономерность отложения взвешенных и донных наносов Жиззакского водохранилища

Джизакское водохранилище как источник орошения открытых оросительных систем играет важную роль в водообеспеченности земель. Гарантированный период запланированного режима водоподачи определяется сроком его заиления. Оно заключается в отложении взвешенных и донных наносов. Но так как взвешенные наносы составляют основную долю (90-95 %) твердого стока, то процесс называется заилением. Донные наносы на протяжении всего периода заиления откладываются полностью, и их объем обычно включают в общий сток наносов. Отложение наносов в верхнем бьефе на определенном этапе заиления настолько сокращает полезную регулирующую емкость водохранилищ, что приводит к нарушению запланированного режима работы водоисточнике и ухудшаем режим работы оросительных систем. Поэтому прогноз сроков заиления необходим для определения параметров водохранилища и плотины, своевременной разработки экономически целесообразных режимов эксплуатации и мероприятий по уменьшению наносных отложений и восстановлению потерянной из-за наносов емкости водохранилища, а также для определения зон интенсивного выпадения мельчайших наносов и удаления их с помощью специальных устройств.

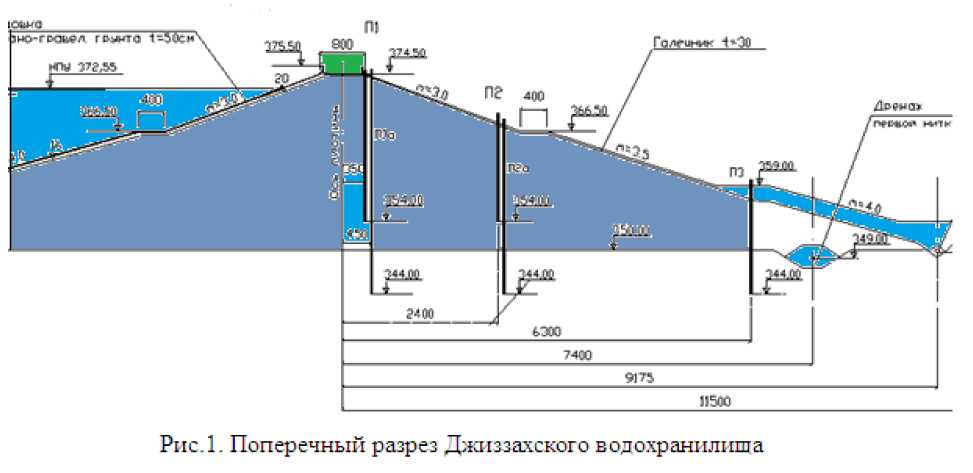
Заиление водохранилищ имеет две стадии. При первой из них происходит полное отложение в верхнем бьефе всех поступающих наносов. На второй - наблюдается отложение наносов с затухающей интенсивностью. Сбросная мутность при этом постепенно возрастает и в конце заиления близка к бытовой.

По режиму работы все гидроузлы подразделяются на подпертые бьефы и водохранилища. Для первых характерен стационарный уровневый режим, а для водохранилищ - переменный.

Методы расчета заиления разработаны только для стационарного уровня. В случае необходимости учета сработки уровней при расчетах заиления принимаются поэтапно параметры водохранилищ, соответствующие разным уровням сработки.

Учет сработки уровня воды для больших водохранилищ не вносит существенных корректив в определение сроков их заиления, так как отложенные за длительную первую стадию наносы, только перераспределяются по длине бьефа без выноса их в нижний бьеф из-за больших объемов водохранилищ при сниженных уровнях воды. Поэтому в ряде случаев расчет выполняется для объема водохранилища при нормально подпертом уровне.

Существует большое количество методов расчета заиления, которые можно подразделить на балансовые и основанные на эмпирических формулах.

Первая группа методов используем различные уравнения баланса наносов. Уравнение pz

b0 l       tt     (1)

используют И.Л. Леви и др. Ряд исследователей используют уравнение (1) в виде конечных разностей:

p)_x - p 2 A t = <1 - z 2 "^l/b (2)

Принимая но внимание, что имеет место формулы для нахождения давления:

p ₁         p ₂

— ⁼ P ; —у-П ; W 3 = < 1 - z 2^ ^b

У      У

Тогда объём заилений или мёртвый объём водохранилища можно представить так: dW   Р’-Р"> (3)

Для нахождения который проф. Латипов К.Ш. пользует системой дифференциальных уравнений Х.А.Рахматулина, описывающих движение многофазных потоков [1].

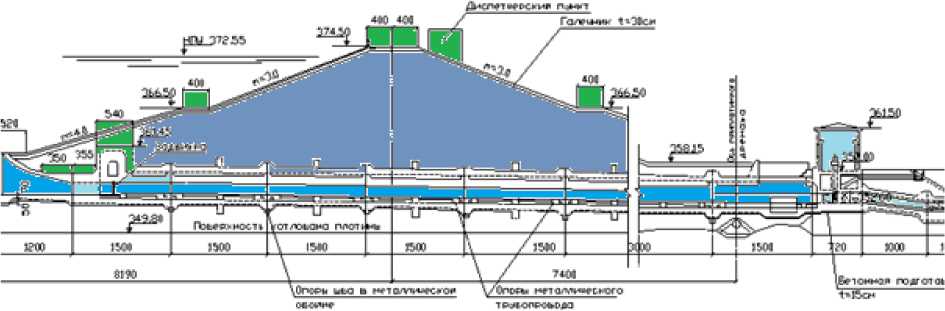
Ри с. 2. Продольный разрез Джиззахского водохранилища

Как было приведено выше отложение наносов в верхнем бьефе на определенном

этапе заиления настолько сокращает полезную регулирующую емкость водохранилищ, возрастанием объёма мертвого объема. Для определения состава наносов и объёма отложений применяется дифференциальное уравнение многофазной жидкости в модели Х.А. Рахматулина. Для применения многофазной модели в моделирование отложения взвешенных и донных наносов, рассмотрим струйное течение многокомпонентной смеси, состоящей из смеси наносов разного диаметра и жидкостей .

Тогда уравнение количества движения и неразрывности смеси идеальных жидкостей запишется в виде [8].

n

d ⁽ n Vn

m

dt

~ gradp-p„F„ + K ^ ( V-V ,),

х =1

n      v _ V т

+ divV n - 2nI_Sn , S * n(S,n = 1, m) , о t              S =1

где K - коэффициент взаимодействия жидкости и других взвешенных наносов; I_Sn -количество фазового превращения. Здесь р_п - приведённая плотность; p_ni - истинная плотность; Но нашем случае фазовые превращения не происходит. V n - скорость n -й фазы жидкой смеси, где :

d⁽ n ) V ^ n dt

——

V n

t

——    ——   ——

+ (V , У)У,

В дальнейшем предположим, что фазовые превращения отсутствуют, тогда I_Sn =0 и уравнения (4.) примет вид

—, = -d^{iv (} PnV_n ) (5)

t

Суммируя уравнения (5) по n , получим уравнение неразрывности для смеси:

t

г 0, где Р = Р! + рг + ... + рт ,

m рV = ^pnVn = P1V1+...+ pmVm - средние величины плотности и скорости в области n=1

смеси с„ = — объемная концентрация n-й фазы смеси. Произведём осреднение по Р массе, умножая на р„ в уравнении (4), для этого суммируем эту систему уравнений по n :

m   d ⁽ " ' V            ™   -

У Рn —р^ = gga^dpP+ У P_nF_n (6) n- 1         ^dt                     n -1

Введем в рассмотрение осредненную силу F по массе, вычисляемую из формулы

m

F       n F n . Тогда можно написать:

n =1

m    d⁽ " ' V             -

У.Рn -^Tn = -gr^adp+ pF (7) n =1         dt

Вычислим изменение количества движения смеси единичного объема K V , так как

d ⁽ "' (P „ V, ) ₌ d' " V ₊ у d P dt         ⁿ dt      ⁿ dt

Откуда:

—► d (pV) dt

m       ( " ' " '

= У у d Pd n n=1        dt

m

n n 1

d⁽ " 'V^ n, dt

Учитывая равенство (7) и уравнение неразрывности:

mⁿ dK = pF + PV^ dt         ±1 "  dt

m

n

n =1

m gradp F gradp  Vn n divVn n=1

Отличаются существующие методы тем, что для расчета наносов используются различные формулы вида p = f q,,h<9_ или p = f ^, h , u_. Ряд авторов при выводе расчетных формул дополнительно прибегают к уравнениям движения потока и постоянства расхода воды. Несколько отличается метод С.Т.Алтунина и И.А.Бузуноза. Он основан на вычислении параметров устойчивого русла, в котором транспортируется заданная нагрузка потока наносов определенной крупности, принимаемая из графика f u . Разность между объемами водохранилища и устойчивых русел принимается за объем заиления. Сток наносов для каждого этапа определяется с учетом части наносов, поступающих в нижний бьеф.

Ко второй группе методов расчета заиления относятся формулы Тейлора, Орта, Г.И.Шамова. Следует отметить, что базирующиеся на уравнениях (3.1) и (3.2) методы прогноза принимают гидравлические элементы русла на участках неизменными в течение расчетного интервала времени, что снижает точность расчетов. Интервалы времени при этом следует принимать такими, чтобы высота отложений не превышала 10-15% расчетной глубины бьефа, что приводит к громоздким вычислениям. Положительной стороной указанных методов является то, что они позволяют получить детальную картину процесса заиления и учесть как период полного отложения наносов в бьефе, так и этап возрастающего выноса наносов в нижний бьеф. Методы, основанные на выражении (3) и эмпирических зависимостях, имеют определенный предел применимости, так как формулы экспоненциального или показательного вида дают по расчету возрастающий вынос наносов уже в начальный период работы гидроузла.

За рубежом изучено изменение нанососдерживающей способности водоемов от различных критериев [19] , Но, к сожалению, там использованы в одних случаях данные по заилению прудов, в других - водохранилищ. Поэтому получены несогласующиеся результаты.

Все возможные случаи заиления верхних бьефов гидроузлов и водохранилищ можно отнести к той или иной из трех расчетных схем отложения наносов в зависимости от интенсивности процесса.

К первой схеме относятся верхние бьефы, в которых с начала эксплуатации наблюдается возрастающий вынос наносов в нижний бьеф по мере заиления верхнего бьефа (только вторая стадия заиления).

Вторая схема характерна для водохранилищ, в которых имеется как первая, так и вторая стадия заиления. По третьей схеме ведется расчет для водохранилищ, в которых период возрастающего выноса наносов мал по сравнению с общим временем заиления, и им можно пренебречь, т.е. только первая стадия заиления.