Моделирование зубофрезерования цилиндрических зубчатых колес

координат X ф Y ф Z ф фрезы 2, совершающей вращательное движение с угловой скоростью ω ф и поступательное движение подачи со скоростью V 1 . На этом рисунке изображены векторы, определяющие взаимодействие заготовки 1 и фрезы 2 в процессе зубофрезерования, а также векторы, описывающие эвольвентный профиль зуба нарезаемого колеса и зуба фрезы.

Рис.1. Система координат

Векторное уравнение процесса зубофрезерования имеет вид:

^Гок + ^Гз + ^Гэ + r = ^Гоф + ^Гпод + r n + ^Гф ,

где rз – вектор, отождествляемый с шириной заготовки; rок – вектор, определяющий базовую установку заготовки в приспособлении, которое используется при зубообработке; rэ – векторная функция эвольвенты; rф – вектор, определяющий точку на зубе модульной фрезы; rоф – вектор, определяющий начальное положение системы координат фрезы в системе координат станка; rпод – вектор подвода фрезы в начальную точку обработки; rп – вектор подачи фрезы в процесс фрезерования; rф – вектор, определяющий точку на зубе модульной фрезы; r – замыкающий вектор между точкой эвольвенты и точкой на зубе фрезы.

Каждый вектор может быть записан в координатной форме. Например, вектор r_ок в принятой системе координат станка запишется :

r ок

0 h пр

где hпр – высота опорной плоскости, на которую устанавливается заготовка 1 относительно стола 2 станка (рис. 2). Вектор r3 в координатной форме выражается функцией rз

B

где В – ширина венца нарезаемого зубчатого колеса.

Векторная функция эвольвенты r_э в системе координат X к Y к Z к заготовки записывается в следующем виде [3]:

rэ

R sin ф   — R ф cos ф

R cos ф_     R ф sin ф

где R – радиус основной окружности; φ – угол поворота прямой вокруг оси зубчатого колеса, соединяющей его центр и точку касания производящей прямой, обкатывающейся по основной окружности.

Вектор r является замыкающим звеном при обкатке. В процессе моделирования зубо-обработки он может быть равен нулю в тот момент, когда происходит профилирование эвольвенты. При этом точка, принадлежащая боковой режущей кромке фрезы, находится в полюсе зацепления эвольвентного профиля зуба колеса и производящей рейки. Большинство точек фрезы последовательно проходят полюс профилирования. Исключение составляют точки вблизи вершины зуба фрезы, которые при обкатке формируют переходную кривую ножки зуба колеса или кривую подрезания. Периферийная режущая кромка зуба фрезы формирует только впадину между зубьями. В каждом случае профилирование всех участков нарезаемых зубьев происходит в плоскости, перпендикулярной оси заготовки, и на кратчайшем расстоянии от рассматриваемой точки фрезы по оси заготовки. В остальные моменты происходит съем металла впадины между зубьями заготовки. Другими словами, съем металла происходит в объеме, заключенном между боковыми поверхностями зубьев во впадине и между торцевыми поверхностями заготовки. При этом объемы снимаемого металла при начальном врезании фрезы в заготовку и при полном врезании отличаются между собой.

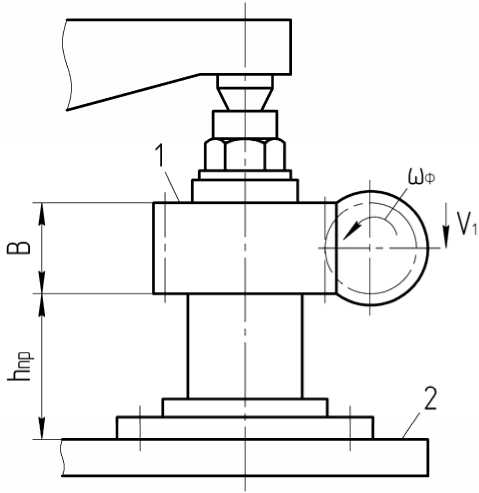
Рис. 2. Установка заготовки в станке

Вектор подвода rпод определяется следующим выражением r . под

— V t

где V – скорость подвода фрезы в начальную точку обработки; t – время подвода фрезы.

Вектор подачи r_п имеет вид:

r

п

-V t

V ₁ t ₁

где V 1 – скорость подачи фрезы в процесс фрезерования; t 1 – время подачи фрезы.

Вектор r ф , описывающий движение точки, принадлежащей профилю каждой из реек червячной модульной фрезы, определяется выражением [4]

Гф = Mr (i, j, k, m) = cos[( n -1)^] sin[(n -1)^] 0

- sin[( n -1)^ ] 0 - ^jsin ф1 cos[( n -1)^]   0 R1cos фх 0          1 - аф1 где M - матрица поворота вокруг оси фрезы ОфZф; r(i, j,.k,.m) - вектор, описывающий режущие кромки зубьев исходной рейки фрезы с учетом винтового движения; i - номер вектора на зубе, j - номер зуба на рейке фрезы; k - номер рейки на фрезе; m - количество точек и номер точки на векторе. Количество точек на векторе может принимать значение от 1 до любого целого числа m в зависимости от требуемой точности расчета; R1 - текущий радиус, который может принимать значения в пределах от величины радиуса внутреннего Rf0 фрезы до радиуса ее наружного цилиндра Ra0; φ1 – текущий параметрический угол, который изменяется в пределах от φ1=0 до φmax; n – номер рейки, который изменяется от 1 до числа зубьев фрезы z0; ψ - угол между зубьями фрезы, ψ=2π/z0; a – параметр, характеризующий движение по винтовой линии вдоль оси фрезы ОфZф. Значение параметра a зависит от угла наклона винтовой стружечной канавки.

Выводы: в работе представлены основные векторные зависимости, определяющие характер взаимодействия нарезаемого зубчатого колеса и червячной модульной фрезы. Сложный процесс взаимодействия профиля зубьев нарезаемого колеса и профиля зубьев фрезы может быть описан алгоритмически, включая в себя относительные вращения заготовки и фрезы, установочные движения и движение инструмента в процессе обработки.