Моделирующий алгоритм процесса распределения работников линейно-кабельного отдела региональной инфокоммуникационной компании

Моделирование бизнес-процесса открывает возможности анализа их последствий на стадии проектирования, и тем самым снижает риск необоснованных затрат.

При имитационном моделировании деятельности компании по предоставлению анализируемой услуги на ЭВМ вместо аналитической модели исследуемого процесса используется его алгоритмическое описание.

Для моделирования процесса на ЭВМ необходимо преобразовать его математическую модель в специальный моделирующий алгоритм. Он представляет собой последовательность некоторых операций, выполняемых ЭВМ.

Построение МА является таким этапом исследования процесса, когда уже решены все принципиальные вопросы создания математического аппарата для исследования. [1]

Построение адекватного МА исследуемого процесса является очень важным и ответственным этапом, поскольку на его основе происходит разработка программы на ЭВМ.

Объектом исследования является процесс региональной ИКК, а именно, процесс распределения работников ЛКО.

Цельисследования–навыходеМАполучитьзна-чение коэффициента загруженности бригад ЛКО.

Задачи исследования:

• -    разработать общую концепцию моделирования;

• -    описать механизм получения целевого значения;

• -    разработать детальную схему МА процесса.

Под общей концепцией моделирования понимается обобщенная функциональная схема используемой модели.

Для достижения цели моделирования в работе предложено использование полиморфной гибридной системы на основе имитационной модели и нейросетевых технологий (ПГС), где результаты работы одной модели – имитационной – используются для функционирования другой – нейронной сети.

Опишем механизм получения целевого значения в контуре работы ПГС. Поток заявок моделируется как рекуррентный (момент прибытия очередной заявки получаем добавлением случайного

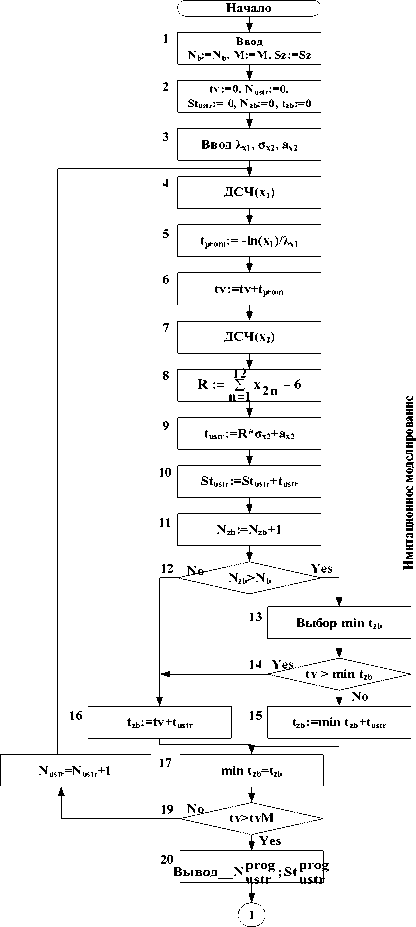
Рис. 1. Моделирующий алгоритм процесса распределения работников ЛКО

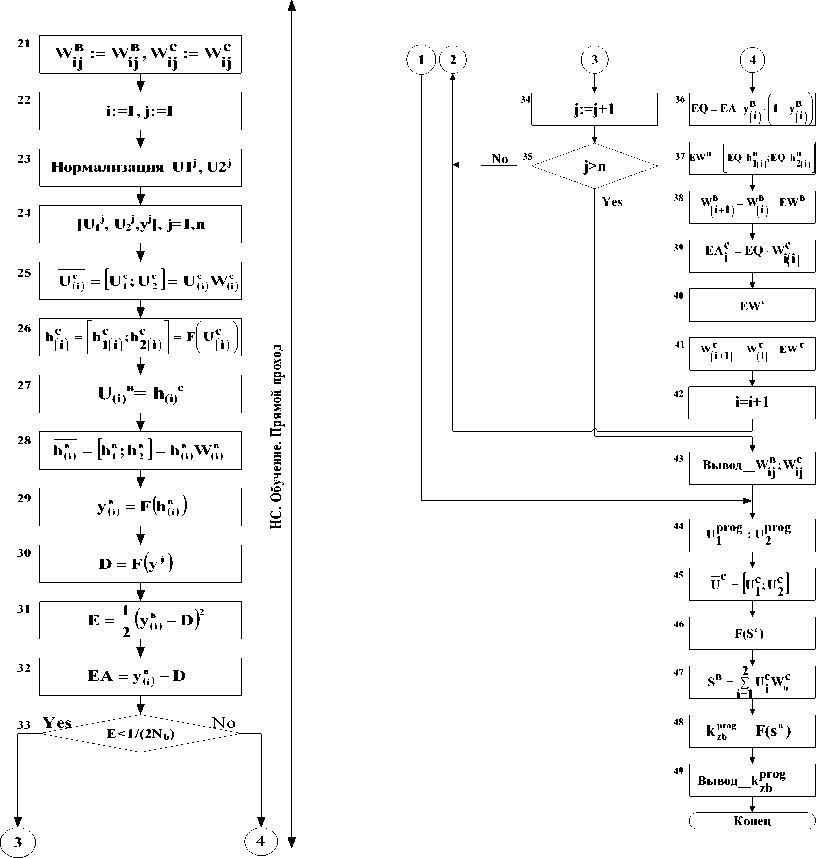
= и z

о и Z

о

Рис. 1. (окончание)

интервала к предыдущему), моменты освобождения каналов – добавлением к текущему моменту случайной длительности обслуживания. [2]

Приведем словарь имитационной модели: tv – текущее время (таймер); Nustr – количество устраненных неисправностей; Stustr – общее время устранения неисправностей; Nzb – количество занятых бригад; tzb – момент освобождения каналов от текущего обслуживания (время занятости бригады); min tzb – наиболее ранний из них; tustr – время устранения неисправности; tprom – момент прибытия очередной заявки; ДСЧ – датчик случайных чисел.

В блоке 1 происходит ввод начальных значений: Nb:=[1, 2, …, Nb], где Nb – число бригад ЛКО; М:=[1, 2, …, 12], где М – месяц моделирования; Sz:=[Sz1, Sz2, Sz3, Sz4], где Sz – сезон моделирования (Sz1 – лето, Sz2 – осень, Sz3 – зима, Sz4 – весна).

Работа модели начинается с установки в нуль таймера (счетчика модельного времени) tv и всех остальных накапливающих счетчиков.

Далее формируется случайный момент tz прибытия заявки (неисправности) и случайное время обслуживания заявки tustr. Текущее время увеличивается на величину tz {tv: = tv + tz}. Значение счетчика Nzb увеличивается на единицу.

В случае Nzb>Nb происходит выбор минимального значения времени освобождения канала mintzb. Если tv > min tzb или Nzb

Далее проверяется время моделирования (блоки 19-26).Если текущее время больше модельного времени, происходит вывод смоделированных значений количества устраненных неисправностей и общего времени на их устранение.В ином случае, цикл моделирования повторяется.

Смоделированные значения количества устраненных неисправностей и общего времени на их устранение являются входными значениями для прогона обученной нейронной сети (блок 51).Обучение нейронной сети проходит в два этапа: прямой проход (блоки 28-40)и обратный проход, то есть корректировка весов (блоки 43-48). Вывод весов связей происходит в блоке 50.

Для обучения нейронной сети необходимаобуча-ющая выборка (задачник),состоящая из примеров. Каждый пример представляет собой задачу одного и того же типа с индивидуальным набором условий (входных параметров) и заранее известным ответом. В рассматриваемом процессе распределения работников ЛКО таким набором условий входных параметров будут являться количество обслуженных заявок и общее время их устранения, а выходным параметром является коэффициент загруженности бригад. Несколько примеров с разными ответами образуют задачник,который располагается в базе данных. Каждая запись базы данных является примером.

В блоке 28 задаются начальные веса связей.В блоке 30 значения количества устраненных неисправностей и общего времени на их устранение из базы данных масштабируются к диапазону 0,1-0,9. В блоке 31 входной образец ставится в соответствие выходному образцу.

Далее на вход скрытого слоя сети подается набор обучающих данных и рассчитывается взвешенный вход для каждого из нейронов скрытого слоя (блок 32). В блоке 33 рассчитывается выход скрытого слоя сети,преобразованный функцией активации.Выход скрытого слоя является входом для выходного слоя (блок 34). Рассчитываем взвешенный вход для выходного слоя точно так же,как и для скрытого слоя (блок 35).Получаем выход сети,преобразованный сигмоидальной функцией активации (блок 36). В то же время рассчитываем желаемое значение выхода сети (блок 37)и вычисляем среднеквадратичную ошибку (блок 38). Далее вычисляем величину скорости реакции ошибки при данном значении выхода сети (блок 39).

В блоке 40 происходит сравнение полученной величины ошибки и допустимое значение ошибки. Если величина ошибки находится в допустимых пределах,веса признаются корректными и сети предъявляется новый входной образец,то есть цикл повторяется. Если же ошибка больше предельно до-пустимой,начинается обратный проход или корректировка весов.

Рассчитываем скорость изменения ошибки сети при изменении средневзвешенного входа выходного слоя(блок43).Далеерассчитываемвекторзначений, на которые следуетскорректировать синоптическую матрицу выходного слоя (блок 44).Изменяем значения весов на входе выходного нейрона (блок 45). Далее определяем реакцию ошибки при изменении активности скрытого слоя для получения корректировочных коэффициентов для скрытого слоя (блок 46).В блоке 47 происходит расчет корректировочных коэффициентов для синоптической матрицы скрытого слоя. Рассчитываем новые веса для скрытого слоя (блок 48). Далее на вход сети предъявляется новый входной образец и осуществляется прямой проход с полученными вновь весами связей.

Прогон сети (блоки 51-56)выполняется подобно прямому проходу при обучении сети.На вход подаются смоделированные с помощью имитационной модели значения количества неисправностей и общего времени на их устранение (блок 51), вычисляем взвешенный вход для каждого из нейронов скрытого слоя (блок 52) и вычисляем выход скрытого слоя сети,преобразованный функцией активации (блок 53).Далее вычисляем взвешенный вход для выходного слоя сети (блок 54) и вычисляем выход сети, преобразованный функцией активации (блок 55).В блоке 56 происходит вывод коэффициента загруженности бригад в моделируемом периоде.

Моделирующий алгоритм процесса распределения работников ЛКО в графической форме представлен на рис. 1. В процессе моделирования используется синхронный моделирующий алгоритм со случайным шагом, когда шаг моделирования Δt есть случайная величина; все элементы системы просматриваются только в момент изменения состояний системы [3].В нашем случае, это момент появления неисправности, и процесс моделирования «синхронизируется» этими моментами.

Выводы

Запись алгоритма для моделирования сложного процесса сразу в виде программы,как правило, представляет значительные трудности. Кроме того, эта запись оказывается весьма неудобной.Нагро-мождение всевозможных деталей,связанных с организацией вычислительной процедуры,делает ее мало обозримой и затрудняет ориентировку в структуре моделирующего алгоритма. Разработанный моделирующий алгоритм используется для получе- ния значения коэффициента загруженности бригад ЛКО.

Данный коэффициент показывает,какая часть бригад «занята/свободна» в рассматриваемый момент времени Т. Знание данного коэффициента позволит руководителю телекоммуникационной компании эффективно распределять человеко-ресурсы, а именно предоставлять сотрудникам очередной отпуск, организовывать курсы повышения квалификации и др.,при этом,данное решение не должно отрицательно повлиять на работу компании в целом (в данном случае – на эффективность обслуживания клиентов).