Модельная задача потери устойчивости кристалла с ГПУ-структурой при растяжении

A model of a single crystal with hexagonal close packed structure has been performed which described its behaviour. According the theories of bifurcation and nonlinear analysis the equation of stability (instability) has been obtained. The grafical solution of the equation and the value of the critical force have been found.

Согласно экспериментальным данным [1], [2] разрушение идеального кристалла при нагружении происходит за счёт сдвиговой деформации, которая характеризуется образованием полос скольжения. Как известно, скольжение происходит в случаях, когда фактор Шмида отличен от нуля. Однако следует ожидать, что при определённых условиях сдвиговая деформация будет развиваться и в случае, когда фактор Шмида равен нулю, то есть когда направление растяжения перпендикулярно плоскости скольжения.

Теоретические исследования такой ситуации были проведены в работах [3], [4], [5]. Используя методы нелинейного анализа, изучалась потеря устойчивости двумерного кристалла при растяжении, атомная решётка которого соответствовала расположению атомов в плоскости (0001) металла, имеющего ГПУ-структуру. Применяя потенциал межатомного взаимодействия Леннарда-Джонса в работе [4] и самого общего вида в работе [5], получены критерии потери устойчивости атомного слоя и определена критическая нагрузка.

Предлагаемая работа является продолжением исследований, проведённых в [3], [5], в которой строится модель, характеризующая потерю устойчивости трёхмерного кристалла при растяжении.

Рассмотрим кристаллическую решётку с ГПУ-структурой и трансляцией решётки а, которая растягивается нагрузкой интенсивности q = const, перпендикулярной базисной плоскости (рис. 1) При малых значениях q кристалл ведёт себя как упругое тело и деформация будет происходить за счёт смещения базисных плоскостей относительно друг друга в направлении приложения нагрузки. В этом случае состояние равновесия кристалла устойчивое. При достижении нагрузки некоторого значения q = q_c кристалл может перейти в неустойчивое положение равновесия, при котором базисные плоскости повернутся и составят некоторый угол с направлением нагрузки, отличный от 90°. При дальнейшем нагружении деформация кристалла будет развиваться за счёт сдвиговых деформаций путём скольжения базисных плоскостей.

Построим модель, которая характеризует потерю устойчивости монокристалла и на основании которой определяется предельное значение нагрузки q_c.

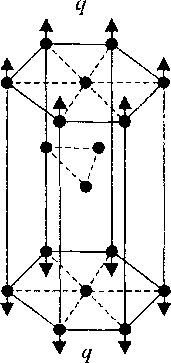
Рис 1. Плотноупакованные слои атомов в напряжённом состоянии

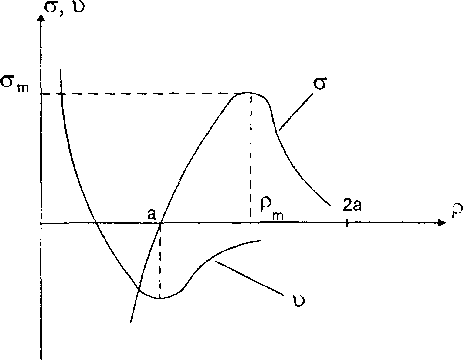
Рис 2. Потенциал межатомного взаимодействия v и сила при растяжении соседних атомов

Предположим, что при нагружении атомы, лежащие в базисных плоскостях, относительно друг друга не смещаются, то есть базисные плоскости представляют собой абсолютно твёрдые тела. В процессе деформации взаимодействуют только соседние атомы, силы межатомного взаимодействия являются потенциальными (сила взаимодействия с двух атомов и межатомный потенциал представлены на рис.2.). При приложении нагрузки q деформацию кристалла можно представить в виде вертикального смещения базисных плоскостей и их поворота.

Нетрудно видеть, что в качестве элементарной ячейки, описывающей поведение всего кристалла, можно выбрать четырёхатомную ячейку, представляющую тетраэдр, один атом которой закреплён, а три других ведут себя как абсолютно твёрдое тело

(рис.З). Атом В₄ в начале координат, а ось OZ проходит через центр тяжести треугольникаЯ/У А₃. Распределённую нагрузку заменим приведённой силой Р, которая приложена в центре тяжести треугольника В^В^В^, в качестве обощённых координат выберем г, ср, 9. Координата г характеризует смещение центра тяжести треугольника В_хВ_гВ_х вдоль оси OZ, угол 6 - поворот треугольника вокруг оси ОУ, угол 9- поворот треугольника вокруг биссектрисы угла В,В_ХВ_Х.

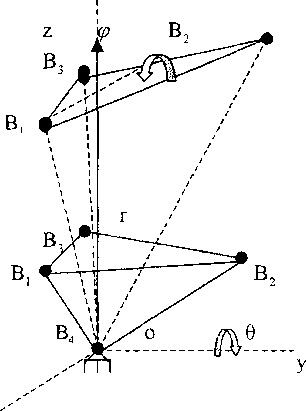
Рис. 3. Четырёхатомная ячейка в недеформированном и деформированном состоянии

Используя методику', описанную в работах [2], [6], [7], выведем условия потери устойчивости кристалла.

Запишем потенциальную энергию ячейки:

П = Е ^(pJ ~Рг

„ „ а² . 2.аг . „ р_х = в в = —^+/‘" ——sin в

V 3 уз р=В,В.=—+г з—== sin 6 + ar cos 6sin

= В3В4 -     +           ® ”ау cos , где v(ps)- потенциальная энергия взаимодействия атома В4 с атомами Bs(s = 1,2,3).

Условия равновесия имеют вид:

П = — = £

6г $=1 др, 6г

ЭП _ £ до(р,) др, _ ₀

Sep »и др, Уф

Значение потенциальной энергии П в исследуемом положении равновесия определяет его устойчивость (неустойчивость), которое в свою очередь определяется через вторые производные П . Составим матрицу

п,тп,6пгфл = пьп„пР ,,п ф#п w где индексы, стоящие у функций П, показывают, что берутся частные производные по соответствующим переменным.

Если матрица А - знакопред елённая положительная, то соответствующее положение равновесия устойчивое; точка, в которой нарушается знакоопределённость, является точкой бифуркации [6], [7].

При вычислении коэффициентов устойчивости П^, Пг6, П1₽, П6<,, ПгЭ, П^, П берём их значени при 9 = ^ = 0, так как исследуется устойчивость соответствующего положения равновесия. Опуская промежуточные выкладки, запишем окончательный результат где

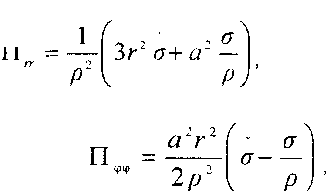
у = ф = 0 ,

а' 2

Р = р.=    + г

So(pJ

- аМедр . 1,2.3.)

9 Р,

Из соотношений (3) следует, что при выполнении неравенств

Зг^го+ —ст > О

Р ’ а - — > О                            (4)

Р матрица А будет знакоопределённой положительной. Знакоопределённость нарушится, когда одно из неравенств (4) переходит в равенство

При обращении в ноль величины П_п происходит потеря устойчивости по г. Теоретически такой случай рассмотреть возможно, но практически это означает разрыв атомных связей, то есть разрушение кристалла предшествует выполнению условий П_п=0.

Величины П ю и П „ обращаются в ноль при достижении расстояния между атомами рс, где рс решение уравнения

0 а „ а- - = 0 .                                (5)

Р

Вид потенциала межатомного взаимодействия металлов мало изучен [1], [4] и в явном виде найти решение уравнения невозможно. Но качественное определение решения (5) можно получить графически. На рис.4 приведены графики, поясняющие смену знака величин П₆₆ и П _w и определяющие значение р_с. Так как р_с< р_т, то потеря устойчивости положения равновесия 6 = ф = 0 произойдёт при силе взаимодействия между атомами о_с , которая меньше временного сопротивления.

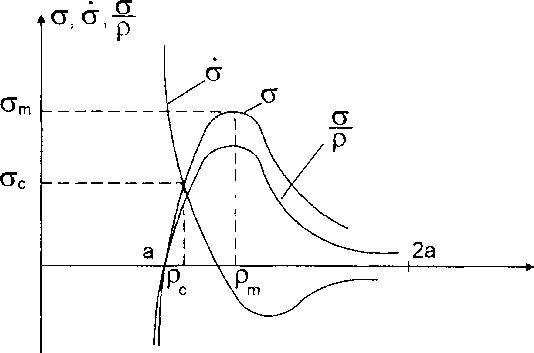
Рис. 4. Графическое решение уравнения (5)

Критическое значение силы Р определяется из уравнения (2).

Зная геометрическую форму кристалла, при помощи несложных преобразований всегда можно перейти от силы Р к нагрузке q и наоборот

Вышеприведённые теоретические выкладки показывают, что сдвиговые деформации могут развиваться и в случае, когда направление растяжения перпендикулярно базисной плоскости. При медленном нагружении кристалла нагрузкой q деформация развивается за счёт увеличения расстояния между базисными плоскостями, при достижении нагрузки q значения q_r происходит потеря устойчивости положения равновесия 6 = 9> = 0, при которой плоскости повернутся и составят некоторый угол с направлением растяжения, отличный от у-, и при дальнейшем нагружении деформация будет развиваться за счёт сдвиговых смещений