Модельно-алгоритмическое обеспечение поддержки принятия решений в информационных системах управления

Vestnik SibGAU

2014, No. 3(55), P. 10–15

MODEL-ALGORITHMIC SOFTWARE DECISION SUPPORT IN INFORMATION SYSTEMS MANAGEMENT

• F. A. Aklanov, D. I. Kovalev, E. V. Tueva, P. V. Zelenkov, K. K. Pershakova

Siberian State Aerospace University named after academician M. F. Reshetnev

• 31, Krasnoyarsky Rabochy Av., Krasnoyarsk, 660014, Russian Federation

The creation of information systems management (IMR) of the enterprise and its model-algorithmic software is explained. System components provide support to the decision maker (DM), after finding the optimal plan reserves distribution between consumers and procurement planning. The objective of the procurement is based on the analysis of sales data, current consumer needs, and the purpose is the procurement plan, in which the level of sales will be maximized. It is shown that an important function of the information management system is to support decision making while ensuring cooperation between all departments and branches of the company and prompt submission of data on the balance of goods in warehouses, its arrival, purchase orders, implementations counterparties and on the current financial status of the enterprise as a whole.

Keyswords: decision support, information management system, model-algorithmic software, transportation problem.

Введение. В связи с расширением различных сфер бизнеса многие предприятия, для того чтобы быть успешными и конкурентоспособными, должны обеспечивать руководство оперативным предоставлением данных о значениях показателей эффективности работы предприятия [1–4]. Для получения такой информации и решения различных управленческих задач создаются системы поддержки принятия решений (СППР) [5]. СППР – это информационноаналитическая система, представляющая собой комплекс математического, программного и информационного обеспечения и предназначенная для автоматизации процессов формирования, выбора и обоснования решений при управлении [6; 7]. В зависимости от уровней управления и решения стратегических, тактических или оперативных задач СППР делятся на крупномасштабные системы поддержки принятия решений [8–10] и информационные системы руководства (ИСР) [11].

В данной статье рассматривается построение ИСР и ее модельно-алгоритмическое обеспечение на примере ИСР Export Management. Важными функциональными задачами в ИСР Export Management являются:

– поддержка лица, принимающего решение (ЛПР), при нахождении оптимального плана распределения запасов между потребителями;

– поддержка ЛПР при планировании закупок (задача планирования закупок реализуется на основе анализа данных продаж, текущих запросов потребителей, причем цель – составить такой план закупок, при котором уровень реализации продукции будет максимален [12]);

– обеспечение взаимодействия всех подразделений и филиалов предприятия;

– оперативное предоставление данных об остатках продукции на складах, поступлениях, заказах, реализациях контрагентам и о текущем финансовом состоянии предприятия.

Оптимальный план распределения запасов. Для нахождения оптимального плана распределения запасов между потребителями в ИСР Export Management используется алгоритм решения многопродуктовой транспортной задачи, где цель – составить такой план перевозок продукции, при котором совокупные транспортные издержки будут минимальны [13]. Рассмотрим решение этой задачи на следующем примере. Предприятие «ЛесЭкспорт» содержит продукцию различного типа древесины: сосна, лиственница, береза, т. е. количество типов продукции К = 3. Головная фирма находится в г. Усть-Илимске (А1), еще два филиала находятся в городах Новосибирск (А2) и Красноярск (А3), запасы продукции указаны в табл. 1, запросы потребителей городов Токио (В 1), Пекин (В2), Новокузнецк (В3), Томск (В4) указаны в табл. 2. Табл. 3 является распределительной таблицей.

Таблица 1

Запасы продукции у поставщиков

Поставщики	Запасы, м3
	Сосна (К1)	Кедр (К2)	Береза (К3)
Усть-Илимск (А1)	a11=200	a12=130	a13=130
Красноярск (А2)	a21=90	a22=50	a23=40
Новосибирск (А3)	a31=25	a32=30	a33=15

Таблица 2

Запросы продукции потребителей

Поставщики	Заявки, м3
	Сосна (К1)	Кедр (К2)	Береза (К3)
Токио (В1)	b11=250	–	b13=100
Пекин (В2)	b21=130	b22=50	–
Новокузнецк (В3)	b31=100	–	b33=70
Томск (В4)	–	b42=65	–

В распределительной табл. 3 указаны стоимости перевозки единицы продукции, где М – очень высокая стоимость. Так как заявки потребителей (В) превышают запасы поставщиков (А) на 55 кубометров, то такая задача называется многопродуктовой незамкнутой транспортной задачей с избытком [13]. Цель решения этой задачи – составить такой план перевозок лесопродукции, при котором совокупные транспортные издержки будут минимальны.

Так как задача многопродуктовая, ее следует разбить на самостоятельные транспортные задачи по виду продукции. В данной задаче три типа древесины, следовательно, количество самостоятельных задач три. Из табл. 3 составим три незамкнутые транспортные задачи и выделим их в табл. 4, 5 и 6.

Таблица 3

Распределительная таблица

(А,В)

B1

B2

B3

B4

Запас, м3

B11

В12

B13

B21

B22

В23

B31

В32

B33

В41

B42

В43

A1

A11

300

М

M

200

M

М

210

М

M

М

M

М

200

A12

M

М

M

M

200

М

M

М

M

М

200

М

130

A13

M

М

300

M

M

М

M

М

210

М

M

М

130

A2

A21

400

М

М

100

M

М

110

М

M

М

M

М

90

A22

M

М

M

M

100

М

M

М

M

М

100

М

50

A23

М

М

400

M

M

М

M

М

110

М

M

М

40

A3

A31

480

М

М

90

M

М

60

М

M

М

M

М

25

A32

M

М

M

M

90

М

M

М

M

М

40

М

30

A33

М

М

480

M

M

М

M

М

60

М

M

М

15

Заявки, м3

250

100

130

50

100

70

65

В=А+55

Таблица 4

Незамкнутая транспортная задача по перевозке сосны

ПО	В11	В21	В31	ЗАПАСЫ
А11	300	200	210	200
А21	400	100	110	90
А31	480	90	60	25
ЗАЯВКИ	250	130	100	–

Таблица 8

Переменные замкнутой транспортной задачи по перевозке сосны

ПО	В11	В21	В31	ЗАПАСЫ
А11	X11	X12	X13	200
А21	X21	X22	X23	90
А31	X31	X32	X33	25
А4ф	X41	X42	X43	165
ЗАЯВКИ	250	130	100	480

Таблица 5

Незамкнутая транспортная задача по перевозке кедра

ПО	В22	В42	ЗАПАСЫ
А12	200	200	130
А22	100	100	50
А32	90	40	30
ЗАЯВКИ	50	65	–

Таблица 6

Незамкнутая транспортная задача по перевозке березы

ПО	В13	В33	ЗАПАСЫ
А13	300	210	130
А23	400	110	40
А33	480	60	15
ЗАЯВКИ	100	70	–

Потребности потребителей продукции составляют 480 м3, в то время как запасы поставщиков 315 м3. Запрос превышает запас на 165 м3, следовательно, эта задача незамкнутая.

Для приведения ее к стандартному виду (задаче замкнутого типа) введем дополнительного фиктивного поставщика, запас которого будет 165 м3, а стоимости перевозок от фиктивного поставщика (А4ф) до потребителя примем равными нулю, так как реально никаких перевозок по этому маршруту выполняться не будет. В итоге получаем замкнутую задачу, эквивалентную исходной (табл. 7).

Таблица 7

Замкнутая транспортная задача по перевозке сосны

ПО	В11	В21	В31	ЗАПАСЫ
А11	300	200	210	200
А21	400	100	110	90
А31	480	90	60	25
А4ф	0	0	0	165
ЗАЯВКИ	250	130	100	480

Обозначим через X ij количество продукции, которое будет вывезено от поставщиков i ( i = 1, 2, 3, 4) и доставлено к потребителю j ( j = 1, 2, 3). Тогда искомый план перевозок, представленный в табл. 8, состоит из 12 управляемых переменных.

Совокупные транспортные издержки на перевозку рассчитываются по следующей формуле:

Z = 300 X11 + 200 X12 + 210 X13 + 400 X21 +

+ 100 X22 + 110 X23 + 480 X31 + 90 X32 +

+ 60 X33 + 0 X41 + 0 X42 + 0 X43,       (1)

где Z – совокупные транспортные издержки; X ij – переменные из табл. 8.

Введение фиктивного поставщика с нулевыми стоимостями никак не влияет на целевую функцию, так как коэффициенты равны нулю.

Ограничения, вытекающие из необходимости удовлетворения потребителей в лесопродукции, следующие:

X11 + X21 + X31 + X41 = 250,

X12 + X22 + X32 + X42 = 130,        (2)

X13 + X23 + X33 + X43 = 100, где Xij – переменные из табл. 8.

Ограничения, связанные с необходимостью расходовать весь запас поставщиков :

Х11 + X12 + X13 = 200,

X21 + X22 + X23 = 90, "  X31 + X32 + X33 = 25,

X41 + X42 + X43 = 165, где Xij – переменные из табл. 8.

Все переменные неотрицательные :

Xij > 0, где Xij – переменные из табл. 8.

В результате имеем замкнутую транспортную задачу линейного программирования: необходимо минимизировать целевую функцию (1) при условии, что на переменные наложены ограничения (2)–(4).

Алгоритм решения задачи:

– исходную информацию вводят в документы «Заказы покупателя», указывается номенклатура, характеристики, количество, пункт назначения (адрес доставки);

• – в справочник «Маршруты» вносятся стоимости перевозок;

  – вычисление целевой функции (этот шаг алгоритма выполняется в два этапа: вначале с помощью

функции СУММПРОИЗВ вычисляют сумму попарных произведений цены перевозки единицы груза от i -го поставщика на количество груза X ij , поставляемого j -му потребителю; затем вычисляется сумма этих промежуточных расходов, т. е. значение целевой функции (1), которую нужно минимизировать);

– исходные ограничения (2)–(4) записывают в преобразованном виде; из регистра «Остатки товаров на складах» запросом извлекаются ограничения (3) на количество продукции, вывозимой от каждого поставщика; из регистра «Заказы покупателей» извлекаются ограничения (2) на количество продукции, поставляемой каждому потребителю;

– методом перебора с наложением ограничений определяется оптимальный план перевозок.

Оптимальный план перевозок, определяющий объемы лесопродукции, вывозимой от i -го поставщика и доставляемой j -му потребителю, представлен в табл. 9. Минимальные транспортные издержки составляют 59 700 у. е.

Таблица 9

Оптимальный план транспортировки сосны

ПО	В11	В21	В31	ЗАПАСЫ
А11	85	76,94049	38,05951	200
А21	0	53,05951	36,94049	90
А31	0	0	25	25
А4ф	165	0	0	165
ЗАЯВКИ	250	130	100	480

С помощью представленного алгоритма решается задача для каждого вида продукции и определяется оптимальный план перевозок продукции от поставщика к потребителю.

Планирование закупок. Для планирования закупок в ИСР Export Management используется метод планирования и управления по точке заказа, когда предприятие формирует задание поставщикам, если объем его запасов опускается до некоторого предо- пределенного минимального уровня [12–15]. Главное достоинство этого метода – это его простота. Планирование и управление по точке заказа можно использовать для управления запасами категории С (по классификации АВС), т. е. сравнительно недорогими изделиями или материалами.

Точка заказа – фиксированный уровень запаса, при достижении которого необходимо организовать следующий заказ на поставку. Точку заказа рассчитывают для систем с фиксированным интервалом между заказами, или иначе систем с постоянным уровнем запасов [11]. Если поставка товаров происходит в установленные сроки или же существует необходимость быстро реагировать на изменение сбыта, для расчета запаса используют систему с фиксированным интервалом между заказами (или с постоянным уровнем запасов). В такой системе не рассматриваются фиксированный размер заказа и издержки управления запасами.

В соответствии с рассматриваемым подходом через постоянные промежутки времени проводится проверка состояния запасов, и если после предыдущей проверки было реализовано некоторое количество запаса, то подается заказ на пополнение запасов. Объем заказа определяется по принципу восполнения запаса до максимального желательного уровня. Схема планирования по точке заказа представлена на рисунке.

Максимальный уровень запасов М рассчитывается по формуле

M = B + S ( L + R ), (5)

где В – страховой запас; S – среднесуточный сбыт; L – время доставки заказа; R – интервал времени между проверками.

В системе управления запасами с двумя уровнями, или Ss -системе, наряду с максимальным уровнем запасов используется точка заказа:

P = B + S ( L + R /2). (6)

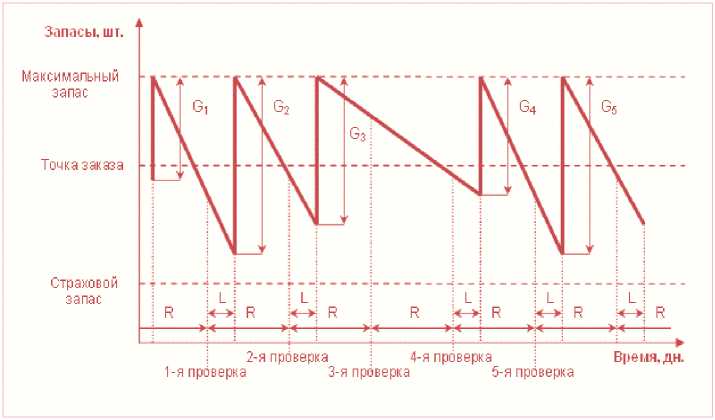
Схема планирования по точке заказа

Поскольку для исполнения заказа требуется определенный период времени, то величина заказываемой партии увеличивается на размер ожидаемого расхода за этот период.

Таким образом, если в момент проверки J <  P , то подается заказ

G = M – J + S ∙ L , (7)

где J – фактический уровень запаса в момент проверки; G – размер заказываемой партии.

В противном случае заказ не подается и процесс повторяется во время следующей проверки.

Алгоритм планирования по точке заказа включает следующие шаги:

– на основании продаж из регистра «Продажи» извлекается количество проданной номенклатуры по периоду, равному месяцу, и делится на количество дней в месяце; таким образом определяем среднесуточный сбыт;

• –    на основании рассчитанных данных среднесуточного сбыта, страхового запаса, времени доставки заказа вычисляется максимальный уровень запасов по формуле (5);

• –    на основании рассчитанных данных среднесуточного сбыта, страхового запаса, времени доставки заказа, максимального уровня запасов вычисляется точка заказа по формуле (6);

  – определяем фактический уровень запаса на момент проверки; для этого делается запрос по регистру «Остатки товаров на складах», получившееся значение сравнивается с точкой заказа; если фактический уровень запаса ниже точки заказа, то на основании рассчитанных данных максимального уровня запасов, фактического уровня запаса, среднесуточного сбыта и времени доставки заказа вычисляется размер заказываемой партии по формуле (7).

Товары, заказанные для пополнения наличных запасов, должны поступать до или точно ко времени, при котором количество запасов достигает своего минимума. Точка заказа должна выбираться так, чтобы уровень наличных запасов в период до ожидаемой поставки не упал ниже минимального уровня и не привёл к дефициту товаров. При этом важно знать продолжительность выполнения заказа и время, необходимое для его поставки. Предсказать время доставки точно не всегда представляется возможным [16]. При неритмичности поставок следует установить поправочный коэффициент времени на всю продолжительность выполнения заказов. Например, если обычно доставки грузов осуществляются в течение двух недель, а задержки в поставках требуют дополнительной недели, можно считать предполагаемое время доставки груза между 14 и 21 числом месяца.

Размер, продолжительность выполнения и момент возобновления заказа (точка заказа) следует устанавливать для каждого товарного наименования на основе результатов предыдущей работы с данным товаром. Время возобновления заказа рассчитывается на основании частоты обращения товара, транспортных тарифов, а также нормативов, минимального и максимального уровня запасов, установленных для данного товара [17].

Заключение. Таким образом, с помощью математических моделей и алгоритмов, описанных в данной работе, обеспечивается компьютерная поддержка принятия решений при реализации важнейших управленческих задач руководством предприятия, а именно, оптимальное распределение запасов между потребителями и планирование закупок, что позволяет предприятию стимулировать потребительский спрос и быть конкурентоспособным. В рамках модельноалгоритмического обеспечения задача планирования закупок реализуется на основе анализа данных продаж, текущих запросов потребителей с целью составления плана закупок, при котором уровень реализации продукции будет максимален. Показано, что важной функцией информационной системы руководства является поддержка принятия решений при обеспечении взаимодействия всех подразделений и филиалов предприятия и оперативное предоставление данных об остатках продукции на складах, поступлениях, заказах, реализациях контрагентам и о текущем финансовом состоянии предприятия в целом.