Модельное описание электронной концентрации в средней ионосфере

В 1997 г. авторами была опубликована полуэм-пирическая модель средней ионосферы (ПЭМ) [1], которая дает связь электронной концентрации N с характеристиками термосферы и индексом солнечной активности. Модель разработана для высот 120–200 км, где в дневное время, как правило, выполняется условие фотохимического равновесия. Многочисленные расчеты, проведенные с помощью модели, подтверждают основную идею, заложенную в нее, идею об универсальном характере модели для среднеширотной ионосферы. Естественно, возникает вопрос о рамках применимости такого типа ПЭМ, о степени точности описания реальных значений N. В какой-то мере ответ можно получить из анализа сравнения модельных расчетов с экспериментальными N. В работе [1] кратко были описаны в общей форме результаты сравнения модельных расчетов с экспериментальными данными. Они свидетельствуют о том, что полученные коэффициенты дают возможность использования ПЭМ в широком диапазоне условий, характеризуемых различием в географическом положении, сезоном года, уровнем солнечной активности в спокойных и возмущенных периодах. Однако вопрос о рамках применимости обсуждаемой ПЭМ неоднократно возникал, поскольку обычно проводимые с ее помощью расчеты относятся к условиям, существенно отличающимся от тех, при которых были получены экспериментальные данные по N, использованные для определения коэффициентов уравнения модели. Такие вопросы возникали потому, что ПЭМ – модель регрессионного типа. Однако при этом упускалось из виду, что здесь используется регрессия особого типа. Дело в том, что промежуточным звеном является опора на характеристики термосферы, очень хорошо описываемые в большинстве случаев ее моделью [2]. Конечно, основой построения ПЭМ явилась разработка уравнения, описывающего в общей форме связь N с параметрами нейтрального газа термосферы и индексом солнечной активности.

Другим обстоятельством , послужившим причи ной постановки вопроса о написании настоящей статьи , служит развитие возможностей использова ния обсуждаемого типа ПЭМ для решения своего рода обратной задачи аэрономии – оценки характе ристик газового состава при использовании ионо сферных измерений N [3].

Учитывая вышесказанное , мы решили предста вить более подробное описание результатов сравни тельного анализа расчетов с экспериментом при раз личных условия х , чем это было сделано в работе [1].

Для этой цели использованы полученные мо дельные расчеты в сравнении их с экспериментом по данным N ( h )- профилей для разных обсерваторий при разных уровнях солнечной активности . Данные по N ( h )- профилям были взяты , в основном , из архи вов МЦД - Б 2.

Уравнение регрессии в разных версиях ПЭМ

Поскольку упомянутое уравнение описывает связь N с параметрами термосферы в общем виде , то представляется справедливой идея об универсаль ности разрабатываемых на основе этого уравнения версий ПЭМ . Эти версии могут быть разнообразны ми , в зависимости от выбора рабочей модели термо сферы , характера исходных экспериментальных данных по N , полученных теми или иными метода ми , а также в зависимости от применения некоторых модификаций уравнения регрессии . Во всех версиях ПЭМ в качестве рабочей используется модель тер мосферы МСИС -86 [2].

Разные модификации уравнения регрессии связаны с различиями в описании непосредственной зависимости N от индекса солнечной активности. Эта зависимость описывается двояко: во-первых, через зависимость концентраций нейтральных газо- вых частиц и их температуры от индекса F10,7 (эта зависимость определяется моделью термосферы); во-вторых, в уравнение введены члены, учитывающие непосредственную связь N с индексом F10.7 . Это та часть зависимости N (F10.7), которая обусловлена эффектом фотоионизации. В первой версии [1] уравнение имело вид

N / N _av = X ₁+ X ₂ [ n ₁/(5 n ₂+ n ₃)]1.5+ X ₃( n ₁/ n ₃) +

+ 0.5 (cos χ )0.5 + X 4 exp[–(T ex – 600)/600] +

+ X 5 ( F – F av ) + X 6 ( F av –150) + X 7 ( F –150)2. (1)

Здесь N – электронная концентрация ; величина N av определяет среднее значение N по всему объему ис пользованных данных отдельно для каждой высоты ; F – индекс солнечного излучения , представляющий собою множитель при величине потока радиоизлуче ния на волне 10.7 см ( в единицах 10^–22 Вт · м ^–2 Гц ^–1); F – ежедневное значение ; F av – значение индекса , осредненного по интервалу 81 день ( за три оборота Солнца ) с центром в данный день ; X j – искомые ко эффициенты уравнения модели ; n ₁, n ₂, n ₃ – концен трации частиц атомарного кислорода , молекул ки слорода и азота соответственно на 120 км ; T ex – тем пература экзосферы , или асимптотическая темпера тура термосферы ; χ – зенитный угол Солнца .

Второй член уравнения (1) описывает зависи мость N от атомных и молекулярных газовых час тиц , третий член дает зависимость от cos χ , которая , в свою очередь , зависит от отношения ( n 1 / n 3 ); чет вертый член описывает связь N с T ex . Роль послед них трех членов заключается в описании зависимо сти N от ионизирующего излучения Солнца .

Коэффициенты уравнения (1) были получены при использовании модели термосферы МСИС -86 для определения n j , T _ex. Исходные эксперименталь ные данные по N получены в Регулярные мировые дни по наблюдениям методом вертикального зонди рования ионосферы в 1957–1967 гг . в обсерватории Москва .

В работе [4] представлена версия ПЭМ , основан ная на уравнении

N / N av = X 1 + X 2 ^.[ n 1 /(5 n 2 + n 3 )]^1.5+ X 3 ^.( n 1 / n 3 )^0.5(cos χ )^0.5+

Вместо трех последних членов уравнения (1) здесь используется один член X 5 ( E / E 0 ), дающий за висимость от относительной величины энергии потока ионизирующего излучения в диапазоне 5–105 нм по модели спектрального распределения интенсивно сти ультрафиолетового излучения Солнца [5]. E 0 – величина E при максимуме солнечной активности , когда F = F av = 250. Следует отметить , что значения E с помощью указанной модели могут быть вычисле ны при задании величин F и F _av.

Достоинством этой формы является возможность использования соответствующей версии ПЭМ для оценок интегральной интенсивности ионизирующего солнечного излучения в определенных условиях. В работе [4] показано, что использование уравнения (2) в качестве основы ПЭМ дает близкие, отличающиеся на единицы процентов, результаты расчетов N в сравнении с версиями, в которых непосредственная связь N с уровнем солнечной активности описывается уравнением (1). В настоящее время наиболее общими в смысле охвата всего диапазона изменения солнечной активности являются те версии, в которых коэффициенты уравнения определяются с использованием экспериментальных данных по N, полученных как при очень высокой солнечной активности, когда Fav достигали значений, больших 240, так и при минимуме солнечной активности. Для этого были использованы данные по N(h)-профилям, полученным в обсерватории Москва [1] в 1957–1958 гг., в 1964–1965 гг. и в некоторые промежуточные периоды.

Сравнение модельных и экспериментальных значений N

Большой объем модельных расчетов был выпол нен с помощью первых версий ПЭМ . В нашем рас поряжении имелись данные по N ( h )- профилям , по лученным из ионограмм для ряда ионосферных обсер ваторий , расположенных как в восточном , так и в за падном полушариях . Наибольшее количество данных относится к периоду МГГ ( Международный геофизи ческий год ) и после него – 1957–1960 гг .

Следует отметить , что , в основном , имеет место одинаковая степень согласия N экспериментальных ( N _э ) и N расчетных ( N _р ), несмотря на то , что расчеты N ( h )- профилей из ионограмм были выполнены раз ными методами и разными исследователями .

Поскольку расчеты по различным версиям ПЭМ дают практически совпадающие между собой ре зультаты , то проводимый анализ согласованности между N э и N р может считаться представительным для типов ПЭМ , упомянутых во втором разделе на стоящей статьи .

Рассмотрим вначале расчеты N в сравнении с экспериментальными данными на высоте 200 км , где отмечаются наиболее выраженные суточные и сезонные вариации в связи с изменениями солнеч ной и магнитной активностей ( диапазон высот от 120 до 200 км ). Имеются экспериментальные дан ные за период очень высокой солнечной активности в 1958 г . В табл . 1 приведены суточные вариации расчетных и экспериментальных значений N 200 для разных месяцев указанного года для обсерватории Вашингтон (Washington) (39° N, 283° E) [6] по сред немесячным данным эксперимента ( N э ) и с исполь зованием для расчетов индексов F _10.7 и А_р ( N _р ).

Из таблицы видно , что различие между расчетны ми и экспериментальными N на высоте 200 км в днев ные часы составляет единицы процентов . При этом интересно отметить , что значения N р на высоте 200 км

Таблица 1

Среднемесячные значения N ₂₀₀ (10¹⁰, м ^–3) по станции Вашингтон , (1958 г .) в сравнении с расчетами

Мес. n\LT 6 7 8 9 10 11 12 13 14 15 16 17 18 F av Апр. Nр 25 34 40 45 49 51 53 53 51 48 43 36 26 240 Nэ 17 33 43 54 54 52 52 50 48 45 40 37 18 Май Nр 24 31 35 39 43 45 47 47 47 44 40 34 27 225 Nэ 22 32 38 42 44 44,5 45 45 43 40 38 32 22 Июнь Nр 21 27 31 34 37 40 42 42 41 38 35 30 23 215 Nэ 26 32 38 42 42 44 44 41 40 39 36 30 25 Авг. Nр 23 30 35 39 42 45 46 47 45 42 38 32 24 236 Nэ 20 32 41 42 43 44 43 43 42 40 37 32 22 Дек. Nр 51 56 58 58 57 54 48 268 Nэ 49 56 60 62 60 51 43 лучше согласуются с экспериментом, чем на более низких высотах. Это можно видеть и в табл. 2, где представлены высотные изменения N в разные часы местного времени для июля 1958 г. В среднем отклонение Nр от экспериментальных dN=[(Np– Nэ)/Nэ]100 % на 200 км в период с 8 до 16 ч LT составило 1 %. В то же время на высотах 120–180 км dN меняется в пределах 6–9 %. Однако в некоторые периоды (начало года, сентябрь, октябрь) отмечались значения Nэ, существенно превышающие (на 20–35 %) величины Np. Можно предположить, что они обусловлены отличием реальных значений параметров термосферы в эти периоды от их модельных значений.

Приведем также данные по обсерватории Эдак (Adak) (52° N, 183° E) для периода максимума сол нечной активности – июля и августа 1959 г ., когда F av =218 и F av =206, соответственно . В табл . 3 показа ны для трех часов LT значения dN (%).

Таблица 2

Высотно - временные изменения величин N _p и N _э (10¹⁰, м ^–3) в июле 1958 г . по станции Вашингтон

LT	N	Высота , км
		120	140	160	180	200
6	N p	10	12	15	18	22
	N э	6	9	11	17	20
8	N p	16	20	25	29	32
	N э	15	20	25	30	34
10	N p	19	24	30	35	38
	N э	21	27	33	36	39
12	N p	20	25	32	38	42
	N э	22	30	36	38	40
14	N p	19	24	30	36	41
	N э	21	29	35	37	39
16	N p	16	20	25	30	35
	N э	18	23	30	34	35
18	N p	10	12	15	19	24
	N э	9	11	17	20	26

Таблица 3

Значения d N (%) по обсерватории Эдак (1959 г .)

Высота , км	июль			август
	LT			LT
	8	12	16	8	12	16
120	–9	–6	1	–4	–5	2
130	–9	–10	–1	–4	–7	1
140	–11	–10	–2	–6	–9	0
150	–10	–10	–3	–6	–9	0
160	–10	–10	–3	–7	–9	–2
170	–10	–8	–3	–8	–8	–3
180	–12	–8	–5	–11	–9	–6
190	–20	–13	–9	–18	–12	–10
200	–27	–18	–12	–21	–14	–12

Можно отметить большое расхождение расчетов с экспериментом на высотах 190 и 200 км , где сильнее роль содержания атомов кислорода . Может быть , это связано с тем , что в рассматриваемый период на дол готе 180° было пониженное в сравнении с моделью МСИС -86 [2] содержание атомарного кислорода .

Продолжая рассмотрение условий при очень высокой солнечной активности , приведем в табл . 4 значения N p и N э в период с 6 до 18 ч LT для высот 160 и 180 км в июле 1959 г . для обсерваторий

Таблица 4

Суточные изменения значений N₁₆₀ и N₁₈₀ по станциям Св . Джона и Монмут для июля 1959 г .

H , км	Святой Джон (St. John's)
	LT	6	7	8	9	10	11	12	13	14	15	16	17	18
160	N p	12	18	26	29	30	31	31	30	30	26	22	18	7
	N э	10	16	23	26	28	28	30	29	28	26	24	20	10
180	N p		26	30	34	34	35	35	34	34	31	28	22	6
	N э		22	26	28	32	33	34	34	32	30	27	22	8
	Монмут (Monmouth)
160	N p	14	19	24	29	32	32	32	32	30	27	24	21	9
	N э	16	20	24	27	29	30	30	30	30	27	24	21	10
180	N p	18	24	29	33	36	37	37	37	34	32	28	12	10
	N э	18	24	28	31	34	36	37	37	35	38	29	19	10

Св . Джона (St. John's) (48° N, 307° E) и Форт Монмут (Ft. Monmouth) (40° N, 286° E). Из этой таблицы также видно хорошее согласие модельных расчетов с экспериментом как по временному ходу , так и по абсолютным значениям N .

Рассмотрим далее условия , характерные для пе риода умеренно повышенной и низкой солнечной ак тивности , по экспериментальным N , полученным в обсерватории Слау (Slough) (51.5° N, 0° E) в 1950 и 1953 гг . [7]. В табл . 5 приведены величины d N на че тырех высотах для 8, 12, и 16 ч LT в июле ( F av =128) и сентябре ( F _av=106) 1950 г . и в июне ( F _av=70) 1953 г . Можно отметить очень хорошее согласие N _p и N _э ле том 1950 г . по данным обсерватории Ватероо (Wathe-roo) (30° S, 116° E), расположенной в Южном полуша рии ( Австралия ). Сравнение приведено в табл . 6.

Таблица 5

Величины d N (%) для станции Слау .

H , км	Июль 1950 г .			Сентябрь 1950 г .			Июнь 1953 г .
	8 ч LT	12 ч LT	16 ч LT	8 ч LT	12 ч LT	16 ч LT	8 ч LT	12 ч LT	16 ч LT
140	4	0	–1	20	10	15	8	8	6
160	–2	0	–3	20	11	17	0	1	0
180	–7	–3	–5	24	8	8	–8	–1	–4
200	–18	–5	–8	9	1	1	–30	–5	0

Таблица 6

Сравнение расчетных и экспериментальных N (10¹⁰, м ^–3) для станции Ватероо в июле 1950 г .

H , км	8 ч LT		12 ч LT		16 ч LT
	N р	N э	N р	N э	N р	N э
140	16	15	21	21	15	15
160	20	20	26	26	19	19
180	24	24	31	30	23	23
200	28	28	35	33	30	29

Хорошо согласуются N р с N э во многие конкретные дни при различной степени геомагнитной возмущенно - сти . В табл . 7 показаны результаты расчетов N 200 для 18 возмущенных дней в апреле – августе 1960 г . в сравне нии с N э для обсерватории Форт Монмут по работе [8]. Всего рассмотрено 140 случаев . Различие между N р и N э в среднем составляет 7 %. В семи случаях это различие превышает 20 %, а в 37 случаях 10 %. Хорошее согласо вание N р с N э в эти дни является подтверждением того , что модель МСИС -86 [2] корректно описывала реакцию газового состава и температуры термосферы на изме нение геомагнитной возмущенности .

Существенные различия между N р и N э отме чаются почти во все зимние дни 1959 г . по данным

Таблица 7

Отношение N _э / N _р ( апрель – август 1960 г ., Форт Монмут .

Дата	А р	9 LT	12 LT	15 LT
29.04	55	0,89	0.68	–
6.05	60	–	0.94	–
7.05	55	1.03	0.96	0.93
11.05	42	0.83	0.89	0.84
5.06	52	0.97	1.06	1.00
7.06	25	1.02	1.00	1.00
9.06	24	1.13	1.00	0.94–
28.06	65	1.04	1.10	–
29.06	36	1.15	1.19	1.10
30.06	36	–	–	1.03
1.07	55	1.09	–	1.07
5.07	20	1.00	0.98	0.98
15.07	40	1.09	–	0.97
18.07	24	–	–	0.99
20.07	35	–	0.99	0.98
21.07	26	1.07	1.18	1.04
17.08	52	1.11	1.05	1.04
18.07	106	–	–	1.00

апрель 2003, 2006 гг .

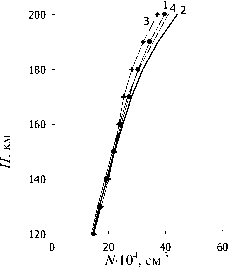
обсерваторий Эдак и Форт Монмут , когда N э пре вышало N р в 1.2–2 раза . C толь же существенные пре вышения N э над N р наблюдались и в некоторые дни зимних месяцев и вблизи равноденствий . Часто они связаны с « положительными » ионосферными воз мущениями . Следует отметить , что сравнение N _р с N _э в такие дни может служить индикатором такого рода возмущений на высотах нижней части области F. Вопрос этот заслуживает особого рассмотрения .

Был также рассмотрен вопрос о том , в какой ме ре модельные расчеты по версии ПЭМ с « москов скими » коэффициентами соответствуют экспери ментальным N , полученным в Иркутске , в Институ те солнечно - земной физики СО РАН , с помощью цифрового ионозонда . Расчеты проведены для всех дней летних периодов ( май – август ) 2003–2005 гг ., в которые проводились измерения . В среднем , по всему сезонному периоду каждого года получено , что d N в 2003 г . равнялось –4 %, а в 2004 и 2005 гг . dN = 4–5 %.

На рисунке приведены высотные профили N ( h ) по среднемесячным экспериментальным и расчет ным значениям N для трех месяцев двух лет . Видно хорошее согласие расчетов с экспериментом во всем рассматриваемом высотном диапазоне .

Заключение

Модельные расчеты электронной концентрации на высотах 120–200 км с помощью развиваемой авторами полуэмпирической модели хорошо согла суются с экспериментальными данными на сред них широтах в восточном и западном полушариях . Имеющиеся расхождения обычно лежат в пределах 10 %. Выявлены случаи , когда расхождение суще ственно увеличивается . Это относится к некоторым зимним месяцам и периодов вблизи равноденствий года очень высокой солнечной активности (1959 г .). В случаях выраженных положительных возму щений в течение части освещенного периода суток отмечаются большие различия между величинами N _э и N _р . По - видимому , в эти периоды имеет место заметное отклонение условий от фотохимического равновесия .

Отмеченное хорошее согласие расчетов с экспе риментом , наблюдающееся в разные сезоны при раз -

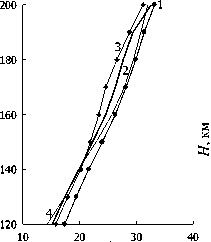
N ·10⁴, см ^-3

июнь 2003, 2007 гг .

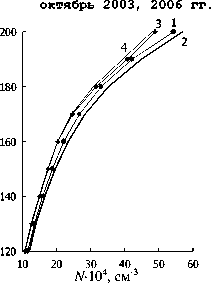
Высотные профили N ( h ) для трех месяцев 2003 и 2006 г .: апреля , июня и октября . Эксперимент ( кривая 1) – 2003 г . Расчет по модели ( кривая 2) – 2003 г . Эксперимент ( кри вая 3) – 2006 г . Расчет по модели ( кривая 4) – 2006 г . Эти обозначения относятся ко всем трем месяцам .

личных условиях солнечной активности и геомаг нитной возмущенности , говорит о достаточно высо кой прогностической ценности обсуждаемой моде ли . В целом можно констатировать оптимальную структуру базового уравнения регрессии модели . Отмеченные различия между величинами N э и N р в значительной мере могут быть обусловлены отличи ем газового состава в конкретных условиях от его описания рабочей моделью МСИС -86. При этом согласие расчетов с экспериментом в разнообразных гео - и гелиофизических условиях обязано качествам используемой модели термосферы .

Все изложенное дает основания заключить , что об суждаемая модель ионосферы может использоваться для оценок отклонений от модельного описания ха рактеристик газового состава в конкретных условиях .