Модельное представление регулируемой дифференциации региональных социально-экономических систем
Автор: Глинский В.В., Серга Л.К., Алексеев М.А.
Журнал: Регионология @regionsar
Рубрика: Экономика и управление народным хозяйством
Статья в выпуске: 3 (124) т.31, 2023 года.
Бесплатный доступ
Введение. В соответствии с законом дифференциации неравномерное развитие элементов системы ведет к ее неоднородности и выступает необходимой предпосылкой процесса эволюции. Ослабляя связи между элементами системы, дифференциация инициирует нарушения в протекании координационных процессов. Преодолеть объективно существующее в организации социально-экономических систем противоречие между координацией и дифференциацией можно путем управления процессом дифференциации элементов системы. Цель статьи - по материалам проведенного исследования построить экономико-математическую модель регулируемой дифференциации региональных социально-экономических систем, позволяющую установить условия и ограничения равновесных траекторий их функционирования, а также определить параметры дифференциации, стимулирующей экономический рост. Материалы и методы. В качестве гипотезы исследования выдвинуто предположение о влиянии внутритерриториальной дифференциации на рост экономики и социально-экономическое развитие региона. Предложен и реализован методологический подход, основанный на представлении модели неравномерности развития территорий в сопоставлении с динамическими характеристиками их экономического развития и предполагающий изучение свойств нелинейных автономных динамических систем. Модель представлена в виде системы дифференциальных уравнений в пространстве значений децильного коэффициента дифференциации и среднедушевого валового регионального продукта. Результаты исследования. Проведенные расчеты на статистических данных по субъектам Федерации за 2 года эмпирически подтвердили выдвинутую гипотезу о влиянии внутритерриториальной дифференциации на экономическое развитие субъектов Федерации. Полученные результаты дополняют теоретические представления о стимулирующих эффектах неравномерности территориального развития и подтверждают непротиворечивость положений концепции регулируемой дифференциации социально-экономического развития территорий. Обсуждение и заключение. Результаты исследования могут применяться при построении динамической экономико-математической модели регулируемой дифференциации региональных социально-экономических систем (субъектов Российской Федерации, страны в целом), которая позволяет определить параметры дифференциации, стимулирующей экономический рост, а также при разработке на ее основе нормативных стратегий территориального развития.
Неравномерное развитие, концепция регулируемой дифференциации, стимулирующий уровень дифференциации, экономический рост, устойчивое развитие
Короткий адрес: https://sciup.org/147241539
IDR: 147241539 | УДК: 332.1 | DOI: 10.15507/2413-1407.124.031.202303.477-497
Текст научной статьи Модельное представление регулируемой дифференциации региональных социально-экономических систем
Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.
Финансирование. Исследование выполнено за счет гранта Российского научного фонда № 22-28-00629 «Методология построения Экологического барометра на основе технологий искусственного интеллекта» .
Original article
Model Representation of Adjustable Differentiation of Regional Socio-Economic Systems
V. V. Glinskiy В , L. K. Serga, M. A. Alekseev
Siberian Institute of Management – Branch of the Russian Presidential Academy of National Economy and Public Administration ( Novosibirsk, Russian Federation ), Novosibirsk State University of Economics and Management ( Novosibirsk, Russian Federation )
Introduction. According to the law of differentiation, the uneven development of the elements of the system leads to its heterogeneity and is a necessary precondition for the process of evolution. By weakening the links between the elements of the system, differentiation initiates disturbances during coordination processes. The objectively existing contradiction in the organization of socioeconomic systems between coordination and differentiation can be overcome by managing the process of differentiation of the elements of the system. The aim of the study is to build an economic and mathematical model of regulated differentiation of regional socio-economic systems (subjects of the Russian Federation, the country as a whole), allowing to establish the conditions and limitations of equilibrium trajectories of their functioning, as well as to determine the parameters of differentiation that stimulates economic growth.
Materials and Methods. The hypothesis of the study is an assumption about the influence of intraterritorial differentiation on economic growth and socio-economic development of the region. The methodological approach based on the representation of the model of uneven development of territories in comparison with the dynamic characteristics of their economic development is proposed and implemented. The approach is based on the study of the properties of nonlinear autonomous dynamic systems. The model is presented in the form of a system of differential equations in the space of values of the decile coefficient of differentiation and gross regional product per capita.
Results. The calculations carried out on statistical data for the constituent entities of the Russian Federation for 2 years empirically confirmed the hypothesis put forward about the impact of intraterritorial differentiation on the economic development of the constituent entities of the Russian Federation. The results obtained complement the theoretical ideas about the stimulating effects of uneven territorial development and confirm the consistency of the provisions of the concept of regulated differentiation of socio-economic development of territories.
Discussion and Conclusion. The scope of application of the research results consists in the possibility of building a dynamic economic-mathematical model of regulated differentiation of regional socioeconomic systems (subjects of the Russian Federation, the country as a whole), allowing to determine the parameters of differentiation that stimulates economic growth, and the development on its basis of normative strategies for territorial development.
RUSSIAN JOURNAL OF REGIONAL STUDIES. Vol. 31, no. 3. 2023 ^^ Keywords : Uneven development, concept of regulated differentiation, “stimulating” level of differentiation, economic growth, sustainable development
Conflict of interests. The authors declare that there is no conflict of interest.
Funding. The research was carried out at the expense of a grant from the Russian Science Foundation No. 22-28-00629 “Methodology for constructing the Ecological Barometer based on artificial intelligence technologies” .
Введение. Эволюция любой системы, в том числе социально-экономической, возможна только при наличии различий в развитии ее компонентов. В конце XIX в. Г. Спенсер предложил подход к представлению эволюции как дихотомии процессов интеграции и дифференциации: «Эволюция в первичном своем виде – переход из менее связной формы в более связную, производимый рассеянием движения, и интеграцию материи, – это истина, но не полная истина. Вместе с переходом от бессвязности к связности идет переход из однообразия в разнообразие. …Вся масса интегрируется и одновременно с тем дифференцируется от других масс; и каждая из ее частей также интегрируется и одновременно с тем дифференцируется от других частей»1.
Закон дифференциации требует разложения исходного целого на его особые элементы как необходимого условия для запуска и усиления эволюционного процесса. Дифференциация ослабляет связи между этими элементами, вызывая нарушения координационных процессов системы, что приводит к неэффективному функционированию, плохой адаптивности, самоорганизации и, в итоге, проявляется в разрушении системы2.
Перенося законы эволюции на развитие социально-экономических систем, академик А. Г. Гранберг в середине 1990-х гг. сформулировал рамочные условия научной проблемы функционирования региональных экономических систем: «Остановлюсь на главных, на мой взгляд, современных трансформационных тенденциях, имеющих место в российском экономическом пространстве. К ним относятся: продолжающееся усиление межрегиональной социально-экономической дифференциации (неоднородности); дезинтеграционные и интеграционные процессы; переход от экономического спада к экономическому росту»3.
Разделение национальной экономики на пространственные социально-экономические системы, отличающиеся неоднородностью и неравномерностью развития, принято называть территориальной дифференциацией.
Неоднородность и неравномерность развития экономического пространства страны является следствием слишком большой дифференциации внутри ее
^^ РЕГИОНОЛОГИЯ. Том 31, № 3. 2023 субъектов (внутритерриториальной дифференциации). Под внутритерритори-альной дифференциацией понимается неравномерность социально-экономического развития территориальных единиц одного уровня внутри изучаемой социально-экономической системы (страны, региона и т. д.) [1].
В основе анализа внутритерриториальной дифференциации лежит взаи-моувязка двух процессов: внутритерриториальная дифференциация, с одной стороны, отражает увеличение разрыва между наиболее и наименее развитыми муниципальными образованиями внутри субъектов Федерации, с другой – влияет на экономическое развитие всей территории, стимулируя рост или ведя к застою.
В отличие от исследований А. Г. Гранберга, который делал упор на межрегиональную дифференциацию, утверждая, что «усиление межрегиональной дифференциации сопровождается расширением территорий особой депрессивности, отсталости, бедности»4, представленное исследование не просто рассматривает неравномерность развития регионов, а переводит изучение названных проблем на внутрирегиональный уровень, выделяя внутритеррито-риальную дифференциацию в специализированный фактор, обусловливающий развитие всего региона.
Определенный уровень территориальной дифференциации социально-экономических систем полезен вследствие создания своего рода пространственной конкуренции, способствующей общему развитию. Однако усиление региональных различий создает проблему для эффективной государственной политики в плане координации социально-экономического развития субъектов страны и приближения их характеристик к уровню более развитых регионов, так как в результате оттока капитала и трудоспособного населения из бедных регионов в более богатые возрастает риск региональных кризисов и межрегиональных конфликтов. Дифференциация в данном случае выступает препятствием для развития, и следовательно, ее необходимо уменьшать.
Таким образом, в организации территориальной системы и связанных с ней социально-экономических процессов наблюдается объективно существующее противоречие между координацией и дифференциацией.
С позиций указанного противоречия доминирующая в настоящее время методология анализа дифференциации социально-экономического развития регионов носит преимущественно фрагментарный характер. Внимание уделяется проблемам диспропорций территориальной организации, дисбалансу развития социально-экономических систем и эффектам дестимулирующего влияния дифференциации на экономический рост. Большинство исследований в практической плоскости сконцентрировано на разработке механизмов противодействия негативным эффектам чрезмерной дифференциации путем сглаживания территориальных различий. При этом научный консенсус в понимании допустимого (равновесного, эффективного) уровня территориальной дифференции не достигнут. Как следствие, возникает угроза того, что преимущественная ориентация на выравнивание социально-экономического состояния территорий выступит искусственно сформированным ограничителем экономического роста.
На снятие указанного выше противоречия и решение вызванных им проблем направлена введенная и апробированная авторами концепция регулируемой дифференциации социально-экономических систем.
Цель статьи – на основе проведенного исследования построить экономикоматематическую модель регулируемой дифференциации региональных социально-экономических систем, которая позволит установить условия и ограничения равновесных траекторий функционирования социально-экономических систем, а также согласовать параметры экономического роста.
Обзор литературы. Теоретической основой многих современных исследований региональной неравномерности развития являются положения теории размещения производительных сил, истоки зарождения которой ведут к древним философам – Аристотелю и Платону. Исследованием проблем пространственного развития экономики основательно начали заниматься в XVIII в. Р. Кантильон, Дж. Стюарт, А. Смит, Д. Рикардо5, в XIX в. – И. Г. фон Тюнен, В. Лаунхардт, А. Вебер, Т. Палан-дер6 [2; 3]. С начала XX в. экономисты В. Кристеллер и А. Лёш в рамках системного подхода сосредоточили внимание на оптимальном размещении населенных пунктов, регионов и отраслей промышленности, на описании основных принципов теории пространственного экономического равновесия7. Во второй половине XX в. на базе исследований У. Изарда8 по адаптации методов макроэкономического анализа и положений теории размещения производительных сил к изучению регионов и межрегиональных отношений сформировалась «региональная наука».
Над проблемами размещения производительных сил и региональной науки работали и многие отечественные исследователи. Наиболее изученными направлениями были проблемы экономического районирования, формирования региональных хозяйственных комплексов и планирования территориального развития. К концу ХХ в. видное место заняло изучение неравномерности регионального развития. В связи с этим возникла необходимость разработки эконометрических инструментов для оценки региональных асимметрий и их влияния на возникновение диспропорций в социально-экономическом положении жителей разных регионов.
Анализ научной литературы последних двух десятилетий по вопросам региональной дифференциации свидетельствует о том, что большинство работ в основном включают варианты решения проблемы типизации регионов по уровням социально-экономического развития. Так, С. Г. Бычкова, О. А. Хохлова в качестве вариантов типологии регионов используют как отдельные показатели (например, валовой региональный продукт, доходы населения), так и системы показателей, характеризующих один или несколько аспектов социально-экономического развития9 [4].
Для проведения типологии регионов С. Г. Бычкова в своей работе применяет методы многомерной классификации, такие как кластерный анализ, дискриминантный анализ10, Ю. С. Зайцева – факторный и компонентный анализ и др. [5]. Достаточно часто исследователями (например, А. И. Костяевым11, В. А. Кривошей [6]) предлагается использовать методику анализа коэффициентов вариации отдельных показателей социально-экономического развития регионов.
Во многих случаях эти исследования направлены на решение прикладных задач, поэтому обобщенные показатели, непосредственно характеризующие уровень дифференциации и ее пороговые значения, не используются. Решение данных вопросов заложило основу наших исследований [7].
Вопросам расчета показателей неравенства (коэффициента Джини, индексов Тейла, Аткинсона, Херфиналя – Хиршмана, Гувера, децильного коэффициента дифференциации и др.) в экономико-статистических исследованиях для измерения неравномерности развития (дифференциации, асимметрии, неравенства различий и т. п.) посвящены работы К. П. Глущенко [8], В. В. Глинского, Л. К. Серга, А. М. Булкиной [1], Л. С. Архиповой, Г. Ю. Гагариной [9], М. Ю. Малкиной [10], В. Г. Теслина [11], Б. Л. Лавровского [12].
В исследовании А. Н. Буфетовой, Е. А. Коломак, направленном на «получение количественных оценок национальной неоднородности в регионах России, используются индексы фракционализации и поляризации с учетом лингвистической дистанции между группами». Показано также, «что в условиях относительно стабильной институциональной среды в стране национальная неоднородность усиливает положительные эффекты экономического развития, при этом потенциал негативных эффектов, заложенных в поляризованном обществе, не развивается» [13, с. 130].
Изучению проблемы дифференциации социально-экономических систем, отдельных ее составляющих и аспектов, ее дестимулирующего влияния на экономическое развитие посвящены работы К. П. Глущенко [8], Б. Л. Лавровского [12], А. Н. Буфетовой, Е. А. Коломак [13], С. В. Баранова, Т. П. Скуфьиной [14], Ю. С. Зайцевой [5], М. В. Морошкиной [15], Е. Н Катаева, Е. А. Погодиной [16] и других ученых.
В ряде публикаций предложены модели математического описания процессов формирования трендов роста и спада, а также их совместного проявления, причем в разновременной проекции12 [17], а также модель функционирования экономических субъектов в пространстве «доходность – ликвидность» [18]. В основе данных моделей лежит решение дифференциальных уравнений, направленных на представление как позитивных, так и негативных воздействий информационных процессов на экономические системы. В. Н. Борисов, О. В. Почукаева в своей статье [19] предлагают метод исследования, находящийся в определенной
RUSSIAN JOURNAL OF REGIONAL STUDIES. Vol. 31, no. 3. 2023 ^^ логической связи с предыдущим и оценивающий влияние инвестиций на динамику конкурентоспособности российской инвестиционной техники; он направлен на определение основных факторов и количественное оценивание эффективности их воздействия на региональный экономический рост.
Считается, что чем меньше разница в уровне развития между территориями, тем более уравновешенным и стабильным является общество. На этом основании большинством исследователей (А. Г. Гранбергом13, Е. А. Коломак [20], А. Ш. Ах-медуевым [21], Л. С. Архиповой, Г. Ю. Гагариной [9]) отмечается отрицательное воздействие чрезмерной дифференциации территориальных образований на их социально-экономическое развитие и необходимость его выравнивания путем дотаций и субвенций.
Обобщая сложившиеся представления, нами предложен теоретико-методологический подход, в рамках которого выдвинута и статистически подтверждена гипотеза, что различия в развитии муниципальных образований внутри регионов имеют двойственный характер: либо способствуют, либо противодействуют экономическому развитию; разработана технология определения оптимального, «стимулирующего» уровня дифференциации с целью выхода региональной экономики на траекторию устойчивого развития; осуществлена типологическая группировка территорий по степени воздействия дифференциации на экономическое развитие и социальную стабильность; выдвинута концепция регулируемой дифференциации социально-экономического развития [7; 22].
Практическое использование указанной концепции выдвигает необходимость рассмотрения региональной экономики с позиций логико-математической модели, позволяющей установить качественные и количественные характеристики состояния равновесия и траектории устойчивого развития. Применение аппарата экономико-математического моделирования позволит найти количественную оценку интервала значений стимулирующей дифференциации, достижение которой позволит положительно воздействовать на экономический рост. Регулирование уровня дифференциации приведет от негативного ее воздействия на социально-экономическое развитие территории к стимулирующему, тем самым будет решена важная народно-хозяйственная проблема – снятие противоречия между координацией и дифференциацией социально-экономического развития территорий. Это реализуется в рамках предлагаемого методологического подхода, основанного на модельном представлении неравномерности развития территорий в сопоставлении с динамическими характеристиками их экономического развития.
Материалы и методы. Для экономико-математического моделирования связи внутритерриториальной дифференциации и тенденций развития регионов предлагается подход, базирующийся на математическом моделировании нелинейных автономных динамических систем, теории устойчивости и модели равновесного экономического роста. Предлагаемый подход расширяет представления об условиях и ограничениях равновесных траекторий функционирования социально-экономических систем, включая элементы согласования параметров экономического роста.
Траектория развития региональной экономики в исследовании определяется уровнем внутритерриториальной дифференциации (при условии отсутствия влияния прочих факторов) и может быть отражена в двумерном пространстве, задаваемом осями: 0x – характеризует уровень внутритерриториальной дифференциации; 0y – индикатор экономического развития.
Модельное представление траектории развития может быть в виде системы дифференциальных уравнений в вышеуказанном двухмерном фазовом пространстве.
В основу расчета уровня внутритерриториальной дифференциации положен децильный коэффициент дифференциации [1; 23]. В указанных публикациях в целях оценки уровня дифференциации муниципальных районов отдельных субъектов Федерации представлена методология построения и практическая технология использования децильного коэффициента дифференциации для пространственных переменных. В качестве индикатора экономического развития применяется уровень валового регионального продукта (ВРП) на душу населения.
Модель включает также управляющие параметры: u 11, u 22, u 12 и u 21. Параметры u 11, u 22, принимая значения 1 или -1, характеризуют динамические эффекты самовоздействия введенных фазовых переменных. Представим автономный (не зависящий от влияния прочих факторов) темп роста уровня территориальной дифференциации через rx > 0, а индикатор экономического развития через r y > 0. Тогда, например, выражение и 11 r x = - r x < 0 при значении параметра и 11 = -1 говорит о том, что величина децильного коэффициента дифференциации снижается и наблюдается эффект предельного насыщения накопленными различиями в социально-экономической системе. Наоборот, выражение и 11 rx = - rx > 0 для и 11 = 1 характеризует динамические особенности функционирования системы, для которой в отсутствии влияния прочих факторов уровень территориальной дифференциации нарастает. Аналогичные рассуждения применимы и к автономным изменениям темпов роста среднедушевого ВРП.
Оставляем в стороне случай, для которого параметры управления и 11 = 0 и и 22 = 0, т. е. текущие уровни переменных, характеризующих внутритеррито-риальную дифференциацию и экономическое развитие, не оказывают прямого влияния на свои будущие состояния.
Между фазовыми переменными, задающими поведение нелинейной автономной системы, допускаем взаимовлияние. Динамические характеристики функционирования социально-экономической системы предполагают существование некоторой связи между изменением уровня территориальной дифференциации и достигнутыми значениями переменных x и у . Одновременно с этим предполагаем, что изменения в региональном развитии также зависят от сочетания фактических значений уровня территориальной дифференциации и уровня экономического развития.
Характер взаимовлияния фазовых переменных задаем параметрами управления u 12 и u 21: плюс (+1), ноль (0) или минус (-1), что предопределяет динамические характеристики системы в целом.
Интенсивность взаимовлияния фазовых переменных зададим через коэффициенты rxy > 0, ryx > 0 и управляющие параметры u 12, u 21.
Исходя из вышеизложенного, траектория регионального экономического развития во взаимосвязи уровня дифференциации территориальных образований и интенсивности их экономического развития, задается системой дифференциальных уравнений:
x = u 11 r x x + u 12 r xy xy
_ y = u 21 ГухХУ + u 22 ГуУ’ где x - уровень внутритерриториальной дифференциации социально-экономического развития субъекта Федерации (децильный коэффициент дифференциации); y – индикатор экономического развития (среднедушевой ВРП субъекта Федерации); rx - темп роста уровня внутритерриториальной дифференциации (x); ry - темп роста индикатора экономического развития (у); x - темп прироста уровня внутритерриториальной дифференциации (x); у - темп прироста индикатора экономического развития (y).
В случае, когда фазовые переменные не оказывают какого-либо влияния друг на друга, т. е. и 12 = 0 и/или и 21 = 0, система (1) имеет единственную стационарную точку – точку тривиального равновесия M (0,0), характеризующую так называемую смерть системы.
Рассмотрим случай, когда u 12 ≠ 0 и u 21 ≠ 0. В сделанных начальных предположениях для системы (1) существует точка равновесия с положительными координатами, если выполнены тождества:
U 11 + U 12 — 0, и 21 + и 22 — 0.
Условия (2) говорят о том, что социально-экономическая система имеет равновесное состояние тогда и только тогда, когда изменения экономического развития и уровня территориальной дифференциации разнонаправлены, т. е. при ослаблении территориальной дифференциации экономический рост стимулирует региональные различия и диспропорции, и наоборот, при усилении территориальных различий экономический рост приводит к их сглаживанию. Зеркальные утверждения возможно выдвинуть и для описания условия противодействия территориальной дифференциации экономическому росту.
I у г
– единственная точка равновесия с положитель-
В этом случае M I —, — rr
V yx xy / ными координатами. Нас интересуют дополнительные условия, налагаемые на
, X I ry У управляющие параметры, при которых решение (x, y) = I —, — rr
V yx xy 7
устойчиво.
При анализе cформулированной модели связи внутритерриториальной дифференциации с экономическим ростом воспользуемся аппаратом анализа, подробно раскрытого в работах М. Интрилигатора14 и Э. Маленво15. Якобиан
( r r примет вид:
системы (1) в точке M I —, — rr
V yx xy /
J ( uii rx + U12 rxyy l u 21 ГухУ
u12 rxyx u21 ryxx + u22 ry ,
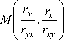
( u11 rx + u12 rx
r u 21 r yx x r
ur r u12 ry r yx u 21 ry + u 22 ry
J
Найдем определитель якобиана det ( J ) = ( u 11 r x + u 12 r x ) ( u 21 r y + u 22 r y ) -- u 12 u 21 r x r y = r x r y ( u 11 + u 12 )( u 21 + u 22 )- u 12 u 21 r x r y •
Используя равенство (2), получаем значения определителя матрицы Якоби: det ( J ) = " u 12 u 21 rxr y .
Необходимым условием устойчивости системы дифференциальных уравнений двух переменных является неравенство det(J) ≥ 0, следовательно, u12 ≠ u21, т. е. соответствующие управляющие параметры должны иметь различные знаки. Рассматриваемое неравенство возможно в случае разнонаправленного взаимного влияния внутритерриториальной дифференции и экономического роста на темпы изменения соответствующих фазовых переменных. А именно, если территориальная дифференциация усиливает экономический рост, то экономический рост должен сглаживать территориальные различия.
В силу равенства (2) имеем: tr( J ) = 0, где tr( J ) – след матрицы J .
Таким образом, собственные значения якобиана имеют нулевую действительную часть, и мы не можем сделать вывод об устойчивости по первому приближению. Проведем исследование на устойчивость, подобрав функцию
^
x
r xy 7
r y
Ляпунова. Если удастся показать, что решение ( x , у ) = —
V yx
устойчиво, то
в силу того, что собственные значения имеют нулевую действительную часть, точка равновесия будет центром.
Осуществим замену переменных:
•
•
x
• X • V by
X, y = lny, x = -, y = -
xy
Получаем систему дифференциальных уравнений
y
J x - u ii r x + u i2 r x yey ) ~ x .
y - u.,Ar e + u^r y 21 yx 22 y и точку равновесия
Mf In r^- ,ln r^
r r
V yx xy J
Рассмотрим случай, когда u 11 = 1, u 22 u 21 = 1. Тогда уравнение (3) примет вид:
-1 и в силу равенства (2) u 12 = -1,
x = r - ry- xxy
~ „x
-. ey
y = r e - r y yx y
Для подбора функции Ляпунова сделаем еще одну замену переменных, которая переместит точку равновесия в начало координат:
rr x = x - In —, y = y - In —. ryx rxy
В результате система (3) имеет вид:
yˆ ln rx r xr re xy xxy . r xˆ ln y v = r e ryx -r y yx y
Проделав определенные арифметические действия, получим систему дифференциальных уравнений xˆ rx rxeyˆ y = rye -ry с точкой равновесия Mˆ 0, 0 .
Рассмотрим функцию Vxˆ,yˆ ry exˆ xˆ 1rx eyˆ yˆ 1. Легко ви деть, что:
-
1) V (0,0) = 0;
-
2) V (Xy y ) > 0, при X^y y ) ^ (0,0);
dV V V
3) x yry
dt x ˆ y ˆ y
Значит, VXxy у ) - функция Ляпунова и точка равновесия M (0,0) - центр.
rx rxe
ryex ˆ ry
А следовательно, и точка равновесия первоначальной системы дифференциаль-
( Г
ных уравнений M y , rx
r
V yx
Случай, когда и 11 = '
также является центром.
r
xy 7
1, u 22 = 1, рассматривается полностью аналогично. Таким
образом, если выполнены условия и 11 + и 12 = 0, u 21 + и 22 = 0, и 12 ф и 21, система (1) имеет единственную точку равновесия с положительными координатами
M
(г
.
r
V yx
r
x , которая является центром.
r
xy У
Приведем графики траекторий на фазовом пространстве при начальных
r
r
условиях из окрестности точки равновесия M y , x
rr
V yx xy /
для случая, когда
r x = r y = r xy = r yx = 1 (рисунок).
Выводы по точкам равновесия подкреплены статистическими расчетами, что подтверждает отсутствие противоречивости с разработанной математической
моделью.

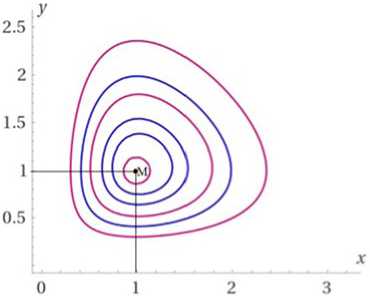
Р и с у н о к. Фазовые траектории развития социально-экономической системы в пространстве «территориальная дифференциация – экономическое развитие»16
F i g u r e. Phase trajectories of the development of the socio-economic system in space “Territorial differentiation – Economic development”
Результаты исследования. Объектом наблюдения в исследовании в качестве изучаемых социально-экономических систем выступают субъекты Российской Федерации, пространственными подсистемами которых являются муниципальные образования (муниципальные районы и городские округа как самостоятельные элементы системы), дифференциация и неравномерность развития которых влияют на общий экономический рост системы. Проверим предложенную модель на статистических данных об уровне внутритерриториальной дифференциации и уровне среднедушевого ВРП как индикаторе экономического развития регионов.
Информационная база исследования построена на данных государственной статистики (Росстата) за 2014, 2015 гг. (см. Приложение17):
-
1) на основе базы данных региональной статистики установлен ВРП на душу населения18 в разрезе субъектов Федерации;
-
2) на основе информации об индикаторах развития муниципальных образо-ваний19 сформирован массив показателей социально-экономического развития муниципальных районов и городских округов, положенный в основу оценки уровня дифференциации в субъектах.
Уровень внутритерриториальной дифференциации рассчитан по формуле децильного коэффициента дифференциации Kd :
K d
D 9СЭР
D 1CЭP
где Kd – уровень внутритерриториальной дифференциации субъекта Федерации; D1СЭР, D9СЭР – первая и девятая децили в упорядоченном по возрастанию множестве значений уровня социально-экономического развития муниципальных образований, входящих в административно-территориальный состав изучаемого субъекта.
Анализ выполнен по 1 782 территориальным единицам 74 из 85 субъектов Российской Федерации. Из расчетов были исключены:
-
1) города федерального значения, в составе которых отсутствуют муниципальные образования;
-
2) автономные округа, входящие в состав субъектов Российской Федерации, учитываемые как их административно-территориальные единицы (Ненецкий, Ямало-Ненецкий и Ханты-Мансийский автономный округ – Югра);
-
3) субъекты, не разрабатывающие информацию по муниципальным районам в полном объеме: Калининградская область, Республика Ингушетия, Республика Крым;
-
4) субъекты, в административно-территориальный состав которых входит очень малое количество муниципальных районов: Сахалинская область и Чукотский автономный округ (один и три муниципальных района соответственно).
Методика оценки уровня социально-экономической дифференциации территориальных единиц в форме интегрального индикатора подробно представлена в нашей более ранней публикации [1]. Для обеспечения сопоставимости показателей, выбранных для расчета уровня (интегрального индикатора) социальноэкономического развития территориальных единиц и имеющих разные единицы измерения, реализована процедура нормирования по модулю максимального значения конкретного показателя для всех анализируемых муниципальных районов и городских округов. Это позволило получить строгие границы варьирования значений полученного индикатора социально-экономического развития муниципальных образований в диапазоне (от -1 до 1). Кроме того, для приведения к однонаправленности показателей, формирующих интегральный индикатор, те из них, которые оказывают негативное влияние на социально-экономическое развитие, учитывались в расчетах со знаком «–».
Выбор временного среза (2014–2015 гг.) для проверки справедливости положений предложенной математической модели и сформированных эмпирических данных обусловлен существенными сдвигами в функционировании национальной социально-экономической системы под интенсивными внешними воздействиями, как на уровне страны в целом, так и в разрезе отдельных территориальных образований.
Сформированные эмпирические ряды значений децильного коэффициента дифференциации протестированы на выбросы. Из рассмотрения исключены данные по Псковской области, поскольку для нее значения показателя составили 50,93 для 2014 г. и 16,219 для 2015 г. Таким образом, в исследовательскую выборку вошли данные по 73 субъектам Федерации.
Статистические расчеты позволили для данных 2014 г. получить следующие оценочные значения системы (1):
X = - 2,1967 x + 0,0005 xy y = - 0,0042 xy + 0,0744 y'
Знаки и значения управляющих параметров соответствуют теоретическим представлениям о равновесии из предыдущего раздела. Для 2014 г. обоснование первого уравнения системы (5) представлено в таблицах 1 и 2, второго – в таблицах 3 и 4.
Т а б л и ц а 1. Статистическое оценивание множественной регрессии первого уравнения системы (5) для 2014 г.20
T a b l e 1. Statistical estimation of multiple regression of the first equation of system (5) for 2014
Регрессионная статистика / Regression statistics
Значение / Meaning
0,925
0,855
0,851
1,573
Множественный R / Multiple R
R-квадрат / R-square
Нормированный R-квадрат / Normalized R-square
Стандартная ошибка / Standard error
Наблюдения / Observations
Т а б л и ц а 2. Статистические оценки множественной регрессии для статистического оценивания первого уравнения системы (5)
T a b l e 2. Statistical estimates of multiple regression for statistical estimation of the first equation of the system (5)
|
Показатель / Indicator |
Коэффициенты / Coefficients |
Нижние 95 % / Lower 95% |
Верхние 95 % / Upper 95% |
|
Переменная x / Variable x |
-2,1967 |
-2,45557 |
-1,93776 |
|
Переменная xy / Variable xy |
0,0005 |
-0,00025 |
0,00141 |
Т а б л и ц а 3. Статистическое оценивание множественной регрессии второго уравнения системы (5) для 2014 г.
T a b l e 3. Statistical estimation of multiple regression of the second equation of system (5) for 2014
Регрессионная статистика / Regression statistics
Значение / Meaning
0,677
0,458
0,442
12,938
Множественный R / Multiple R
R-квадрат / R-square
Нормированный R-квадрат / Normalized R-square
Стандартная ошибка / Standard error
Наблюдения / Observations
Т а б л и ц а 4. Статистические оценки множественной регрессии для статистического оценивания второго уравнения системы (5)
T a b l e 4. Statistical estimates of multiple regression for statistical estimation of the second equation of system (5)
|
Показатель / Indicator |
Коэффициенты / Coefficients |
Нижние 95 % / Lower 95% |
Верхние 95 % / Upper 95% |
|
Переменная xy / Variable xy |
-0,0042 |
-0,0121 |
0,0037 |
|
Переменная y / Variable y |
0,0744 |
0,0496 |
0,0992 |
Данные 2015 г. проявили следующие характеристики системы (1):
5с = - 0,5749 x + 0,0002 xy y = - 0,0173 xy + 0,1696 y ,
что также не противоречит ранее выдвинутым теоретическим положениям.
Представим результаты проведенного эксперимента для 2015 г.: обоснование первого уравнения системы (6) в таблицах 5 и 6, второго – в таблицах 7 и 8.
Т а б л и ц а 5. Статистическое оценивание множественной регрессии первого уравнения системы (6) для 2015 г.
T a b l e 5. Statistical estimation of multiple regression of the first equation of system (6) for 2015
|
Регрессионная статистика / Regression statistics |
Значение / Meaning |
|
Множественный R / Multiple R |
0,515 |
|
R-квадрат / R-square |
0,265 |
|
Нормированный R-квадрат / Normalized R-square |
0,244 |
|
Стандартная ошибка / Standard error |
0,918 |
|
Наблюдения / Observations |
73 |
Т а б л и ц а 6. Статистические оценки множественной регрессии для оценивания первого уравнения системы (6) для 2015 г.
T a b l e 6. Statistical estimates of multiple regression for estimating the first equation of system (6) for 2015
|
Показатель / Indicator |
Коэффициенты / Coefficients |
Нижние 95 % / Lower 95% |
Верхние 95 % / Upper 95% |
|
Переменная x / Variable x |
-0,5749 |
-0,81017 |
-0,33972 |
|
Переменная хy / |
0,0002 |
-0,00019 |
0,00066 |
Variable хy
Т а б л и ц а 7. Статистическое оценивание множественной регрессии второго уравнения системы (6) для 2015 г.
T a b l e 7. Statistical estimation of multiple regression of the second equation of system (6) for 2015
Регрессионная статистика / Regression statistics Значение / Meaning
|
Множественный R / Multiple R |
0,825 |
|
R-квадрат / R-square |
0,681 |
|
Нормированный R-квадрат / Normalized R-square |
0,672 |
|
Стандартная ошибка / Standard error |
18,641 |
|
Наблюдения / Observations |
73 |
Т а б л и ц а 8. Статистические оценки множественной регрессии для оценивания второго уравнения системы (6) для 2015 г.
T a b l e 8. Statistical estimates of multiple regression for estimating the second equation of system (6) for 2015
|
Показатель / Indicator |
Коэффициенты / Coefficients |
Нижние 95 % / Lower 95% |
Верхние 95 % / Upper 95% |
|
Переменная xy / Variable xy |
-0,0173 |
-0,03195 |
-0,00258 |
|
Переменная y / Variable y |
0,1696 |
0,12886 |
0,21040 |
Полученные оценочные значения систем (5) и (6) позволяют определить точки равновесия между внутритерриториальной дифференциацией и экономи-
(г
-
Г
V 'yx
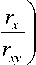
для соответству-
ческим ростом с положительными координатами
M
ющих периодов. Результаты вычислений приведены в таблице 9.
Т а б л и ц а 9. Характеристики точек равновесия системы (1) для 2014–2015 гг.
T a b l e 9. Characteristics of equilibrium points of system (1) for 2014–2015
|
Показатель / Indicator 2014 2015 |
Коэффициент роста / Growth coefficient |
|
Равновесное значение внутритерриториальной 17,79 9,82 дифференциации, коэффициент / Equilibrium value of intraterritorial differentiation, coefficient Равновесное значение валового регионального продукта на 3 797 2 469 душу населения, тыс. руб. / Equilibrium value of the gross regional product per capita, thousand rubles |
0,552 0,650 |
Проведенные вычисления на основе построенной модели (табл. 9) выявили недостаточный (ниже равновесного значения) уровень внутритерриториальной дифференциации для всех субъектов Федерации. Одновременно с этим, на имеющихся эмпирических данных, наблюдаем и недостаточный уровень экономического развития (ниже 3 797 тыс. руб. и 2 469 тыс. руб. в 2014 и 2015 гг. соответственно). Таким образом, в рассматриваемые периоды внутритеррито-риальная дифференциация носила дестимулирующий характер.
Развитие субъектов Федерации в 2014 г. и переход к 2015 г. свидетельствует о сжатии траектории развития экономики России и движении точки равновесия по направлению к так называемой смерти системы ( M (0,0)). Уменьшение равновесного значения валового регионального продукта на душу населения свидетельствует о влиянии экономических санкций на экономику России в 2014–2015 гг., оценочное значение которого позволяет получить построенная модель. Если применить значения коэффициента темпа роста равновесного значения ВРП на душу населения в анализируемых годах (2469 / 3797 = 0,65) к ВВП России в 2014 г. (2 трлн 057 млрд долл. США21), то расчетное (модельное) представление ВВП России в 2015 г. составляет 1 трлн 337 млрд долл. США, при фактическом значении – 1 трлн 363 млрд. Различия в оценках объясняются в том числе валютной политикой Центробанка России. Модельная оценка количественного сжатия (при стабильном состоянии валютных курсов) дает значения негативного воздействия территориальной дифференциации в интервале от 300 до 350 млрд долл. США ( 2057 ⋅ 0,552 0 650 ).
Обсуждение и заключение. Проведенные расчеты на статистических данных по субъектам Федерации за 2 года эмпирически подтвердили выдвинутую гипотезу о влиянии внутритерриториальной дифференциации на экономическое развитие субъектов Федерации. Модельный подход предлагает определенное расширение представлений об условиях и ограничениях равновесных траекторий функционирования социально-экономических систем, включает в себя элементы согласования параметров экономического роста и тем самым развивает положения концепции регулируемой дифференциации.
В рассматриваемых модельных представлениях экономическое развитие территории имеет равновесное состояние тогда и только тогда, когда тенденции, характеризующие экономический рост и уровень территориальной дифференциации, разнонаправлены, при этом экономический рост противодействует дальнейшему усилению территориальной дифференциации, а рост территориальной дифференциации препятствует экономическому спаду.
Доказано, что точка равновесия рассматриваемой социально-экономической системы является центром, так что траектория развития системы в пространстве фазовых координат (внутритерриториальная дифференциация, экономическое развитие) замкнута.
Эмпирически установлены точки равновесия с положительными координатами
M
r y, r
V yx
^
x , позволяющие в том числе определить предельный уровень терри- r
xy 7
ториальной дифференциации, уровень, выше которого она будет способствовать экономическому росту. Таким образом, точки равновесия выступают основой
для определения пределов уровня стимулирующей дифференциации развития региона (страны).
Предложенное модельное представление вносит определенный вклад в разработку теории стимулирующей неравномерности. Развитие исследования видим в расширении временного ряда, построении типологической группировки регионов по характеру взаимовлияния фазовых переменных и разработке нормативных стратегий развития региональных единиц, применении выдвинутых модельных представлений к иным объектам наблюдения, подверженным влиянию дифференциации.
Список литературы Модельное представление регулируемой дифференциации региональных социально-экономических систем
- Глинский В. В., Серга Л. К., Булкина А. М. Дифференциация муниципальных образований как фактор экономического развития территорий // Вопросы статистики. 2016. № 8. С. 46-52. URL: https://voprstat.elpub.ru/jour/artide/view/377 (дата обращения: 25.01.2023).
- Анимица Е. Г., Анимица П. Е., Денисова О. Ю. Эволюция научных взглядов на теорию размещения производительных сил // Экономика региона. 2014. № 2. С. 21-32. https://doi. org/10.17059/2014-2-2
- Жаркова Е. С. Экономические теории размещения производства: от штандорта к кластерам // Вестник Санкт-Петербургского университета. Сер. 5: Экономика. 2011. № 1. С. 145-150. URL: https://economicsjournal.spbu.ru/article/view/2812 (дата обращения: 25.01.2023).
- Хохлова О. А. Статистическая оценка социально-экономической асимметрии муниципальных образований региона // Вопросы статистики. 2006. № 2. С. 32-38. EDN: HTBYZD
- Зайцева Ю. С. Межрегиональная дифференциация в странах БРИК: возможности оценки // Мировая экономика и международные отношения. 2010. № 5. С. 44-51. https://doi. org/10.20542/0131-2227-2010-5-44-51
- Кривошей В. А. Государственное регулирование региональной дифференциации уровня и качества жизни населения // Фундаментальные и прикладные исследования кооперативного сектора экономики. 2013. № 6. С. 35-40. URL: https://www.ruc.su/science/publications/nauchno_te-oreticheskiy_zhurnal/ (дата обращения: 25.01.2023).
- Глинский В. В., Серга Л. К. Регулируемая дифференциация как механизм устойчивого развития // Научные труды Вольного экономического общества России. 2020. Т. 222. С. 297-310. https://doi. org/10.38197/2072-2060-2020-222-2-297-310
- Глущенко К. П. Об оценке межрегионального неравенства // Пространственная экономика. 2015. № 4. С. 39-58. https://doi.Org/10.14530/se.2015.4.039-058
- Архипова Л. С., Гагарина Г. Ю. Пространственная дифференциация регионов РФ и их конкурентоспособность // Вестник Удмуртского университета. Экономика и право. 2015. Т. 25, № 4. С. 19-27. URL: https://journals.udsu.ru/econ-law/article/view/3359/3301 (дата обращения: 25.01.2023).
- Малкина М. Ю. Оценка факторов конвергенции/дивергенции российских регионов по уровню бюджетной обеспеченности на основе декомпозиции индексов Тейла - Бернулли // Пространственная экономика. 2016. № 3. С. 16-37. https://doi.Org/10.14530/se.2016.3.016-037
- Теслин В. Г. Асимметрия развития инвестиционных процессов в Центральной России // Транспортное дело России. 2009. № 1. С. 22-25. EDN: JXVGWD
- Лавровский Б. Л. Территориальная дифференциация и подходы к ее ослаблению в Российской Федерации // Экономический журнал Высшей школы экономики. 2003. Т. 7, № 4. С. 524-537. URL: https://ej.hse.ru/2003-7-4/26560890.html (дата обращения: 25.01.2023).
- Буфетова А. Н., Коломак Е. А. Национальная неоднородность в регионах России: оценка, изменение, влияние на экономическое развитие // Вопросы экономики. 2021. № 1. С. 120-142. https://doi.org/10.32609/0042-8736-2021-1-120-142
- Баранов С. В., Скуфьина Т. П. Сравнительная динамика экономического роста и межрегиональная дифференциация территории российского Севера // Вопросы статистики. 2015. № 11. С. 69-77. URL: https://voprstat.elpub.ru/jour/article/view/285 (дата обращения: 25.01.2023).
- Морошкина М. В. Межрегиональная дифференциация субъектов Российской Федерации // Экономический анализ: теория и практика. 2014. № 45. С. 20-26. URL: https://www.fin-izdat.ru/journal/analiz/detail.php?ID=64112 (дата обращения: 25.01.2023).
- Погодина Е. А., Катаев Е. Н. Оценка уровня и глубины дифференциации экономического и социального развития регионов Приволжского федерального округа // Национальные интересы: приоритеты и безопасность. 2014. № 21. С. 30-37. URL: https://www.fin-izdat.ru/journal/ national/detail.php?ID=62012 (дата обращения: 25.01.2023).
- Минаков В. Ф. Информационные процессы в формировании ажиотажных циклов // Развитие территорий. 2021. № 2 (24). С. 76-82. https://doi.org/10.32324/2412-8945-2021-2-76-82
- Алексеев М. А. Моделирование финансового цикла и поведение компании в информационном пространстве финансового рынка // Вестник НГУЭУ 2017. № 3. С. 131-146. URL: https:// nsuem.elpub.ru/jour/article/view/1063/661 (дата обращения: 25.01.2023).
- Борисов В. Н., Почукаева О. В. Развивающее импортозамещение как следствие роста конкурентоспособности инвестиционной техники // Развитие территорий. 2021. № 2 (24). С. 10-18. https://doi.org/10.32324/2412-8945-2021-2-10-18
- Коломак Е. А. Пространственное развитие России в XXI в. // Пространственная экономика. 2019. Т. 15, № 4. С. 85-106. https://doi.org/10.14530/se.2019.4.085-106
- Ахмедуев А. Ш. Проблемы чрезмерной поляризации уровня социально-экономического развития регионов России и императивы модернизации государственной региональной политики // Региональные проблемы преобразования экономики. 2017. № 6. С. 37-51. URL: http://www. rppe.ru/new/index.php/rppe/article/view/589/513 (дата обращения: 25.01.2023).
- Glinskiy V. V., Serga L. K., Alekseev M. A. Territorial Differentiation as the Factor of Sustainable Economic Development // Procedia Manufacturing. 2020. Vol. 43. Pp. 263-268. https://doi. org/10.1016/j.promfg.2020.02.152
- Investigation of Correlation between the Regions Sustainability and Territorial Differentiation / V. Glinskiy [et al.] // Procedia Manufacturing. 2017. Vol. 8. Pp. 323-329. https://doi.org/10.1016/j. promfg.2017.02.041


