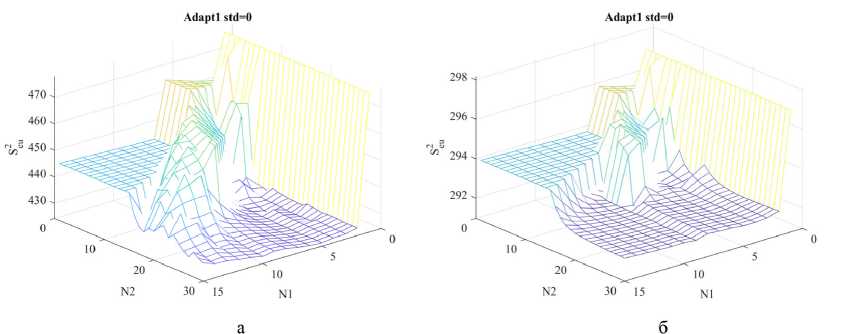
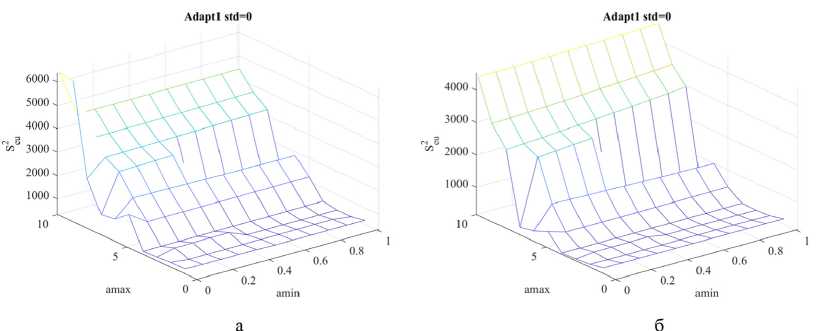
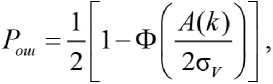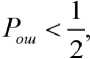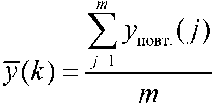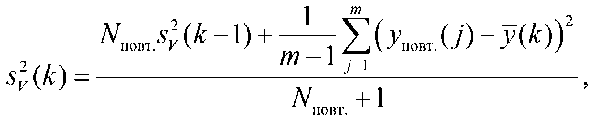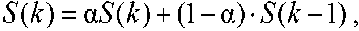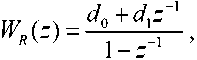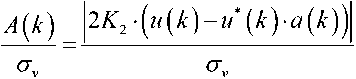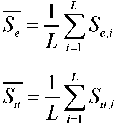Модельно- ориентированное проектирование дискретной одномерной системы экстремального управления

Системы экстремального регулирования, как класс адаптивных систем управления, предложены, теоретически обоснованы и реализованы в 20–70‑х годах прошедшего столетия [1–3].

В настоящее время реализуются сложные технологические процессы, автономные мобильные платформы, цифровизация технологических процессов, широкие возможности микроконтроллеров, рекуррентные процедуры идентификации и управления открывают новые горизонты для систем экстремального управления (СЭУ).

СЭУ позволяют адаптироваться к меняющимся условиям, оптимизировать свои параметры в реальном времени и применяются в ситуациях, когда точная математическая модель системы неизвестна или слишком сложна для аналитического решения.

В традиционном применении методов поиска экстремума предполагалось, что оптимальные параметры объекта управления меняются довольно медленно. При этом игнорировались динамические характеристики системы, и алгоритм анализировался и проектировался с использованием традиционных техник «статической оптимизации» [5].

Существует два основных подхода к поиску экстремума:

– c использованием непрерывного зондирующего сигнала для исследования устойчивого состояния объекта, из которого может быть получен приближенный неявный градиент, как описано в [6, 7].

– с использованием (повторяющейся) последовательности постоянных зондирующих входов, которые используют подходы методов численной оптимизации [8, 9].

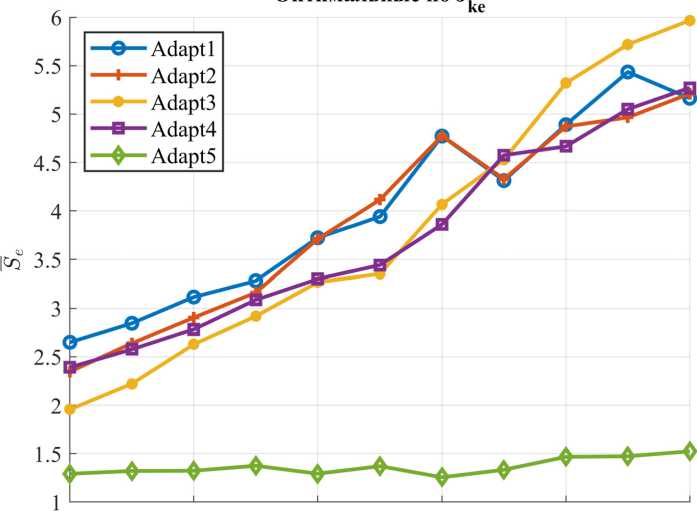
Адаптивные системы управления включающие, экстремальные регуляторы, имеют два способа реализации. В первом способе экстремальный регулятор в качестве адаптера регулятора с обратной связью. В [10] используется экстремальный регулятор с зондирующим сигналом для настройки параметров ПИД регулятора по бегущему среднему квадрата ошибки. В [11] поиск экстремума используется для настройки коэффициента усиления безмодельного регулятора. В [6] экстремальный регулятор настраивает зону нечувствительности для пропорционального регулятора.

Во втором способе экстремальный регулятор напрямую меняет управляющее воздействие. В [9] описано семейство экстремальных регуляторов, основанных на методах нелинейного программирования.

Оба способа реализации требуют определения величины шага поиска. В [12] величина шага поиска на каждом шаге уменьшается по детерминированному закону. Такой способ прост в реализации, но обладает множеством недостатков, таких как медленная сходимость, чувствительность к начальному значению шага поиска, отсутствие адаптивности к поверхности целевой функции. Эти недостатки могут приводить к замедлению процесса поиска, субоптимальной траектории поиска, установлению колебательного процесса в районе оптимума и застреванию в локальном оптимуме.

В статьях [5, 9, 13] используется алгоритм линейного поиска шага, описанный в [14]. Такой подход позволяет адаптивно определять шаг поиска, однако содержит недостатки, среди которых: повышенная вычислительная нагрузка; зависимость от начального направления и шага; повышенная сложность в многомерных пространствах.

В предлагаемой статье изложен подход модельно‑ориентированного проектирования и исследования модифицированных шаговых алгоритмов поиска на базе одномерного последовательного симплексного метода (ПСМ) и СЭУ с оптимизируемым ПИ‑регулятором.

Постановка задачи

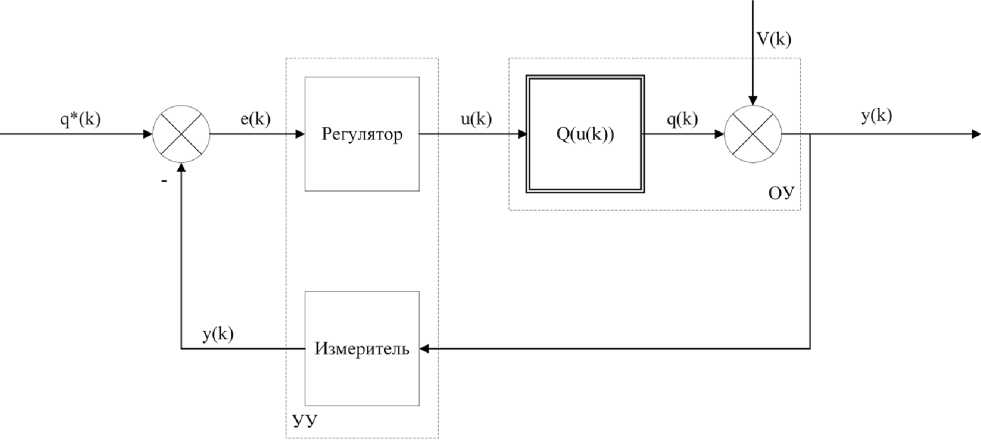
Модель объекта управления ym^Q^+vm,                        (1)

где Q (·) – неизвестная унимодальная функция, y ( k ) – измеренное (вычисленное) значение целевой функции ОУ в момент времени k ; V ( k ) – аддитивная помеха (не измеряемая); u ( k ) – управляющее воздействие (текущая точка поиска, управление).

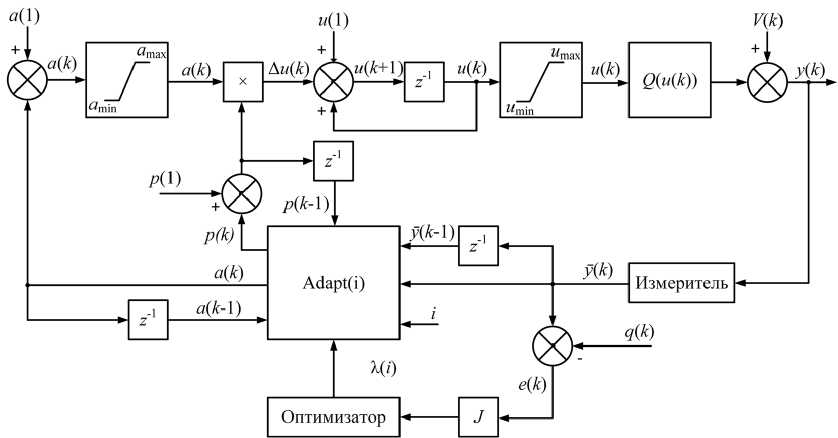
Структурная схема дискретной одномерной СЭУ представлена на рис. 1.

Задача экстремального регулирования состоит в том, чтобы текущее управление обеспечивало экстремум измеряемой (вычисляемой) целевой функции.

Q(u(k\) ^ min ,                                                (2)

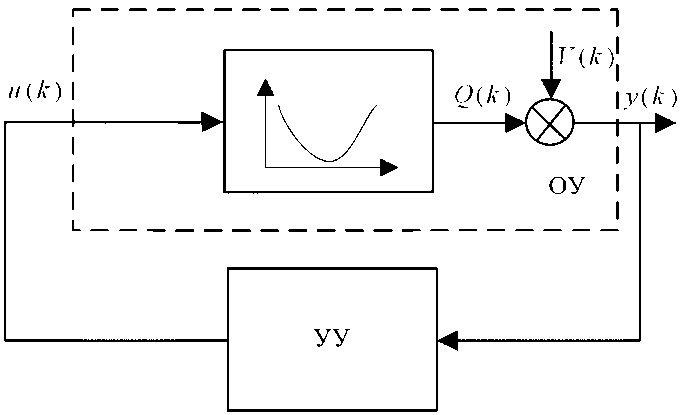
Рис. 1. Структурная схема СЭУ: УУ – устройство управления; ОУ – объект управления

Fig. 1. Structural diagram of the ECS

где ^ = {M^min ^(^Wn^}

Процесс поиска минимума реализуется рекуррентной процедурой

u(k +1) = u(k) + Au(k)

’, k = 1, 2, 3, …, N ,

где Au(k) = a(k) • p(k) – изменение управляющего воздействия на k ‑м шаге поиска;

p(k) = p(k - i)sign [-Av(^)] =

p(k-\\ ky(k)<0,

-p(k-l\ ^y(k)>Q,

– направление поиска; ^min “ Cl(k) < ^_max

величина рабочего шага, определяется технологическими режимами оборудования; ^k^y^-y^k-l) – приращение выходной переменной.

Постановка задачи (2) и метод решения (3) – это классическая постановка задачи нелинейного программирования. Поскольку вид функции неизвестен, то метод решения – поисковая оптимизация (методы нулевого порядка) непосредственно на ОУ.

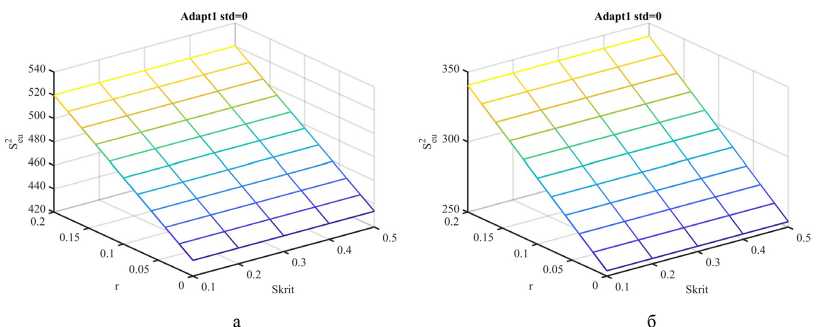
Эффективность СЭУ определяется свойствами ОУ и УУ. Свойства ОУ изменить нельзя, а вот свойства УУ определяются при проектировании СЭУ. Эти свойства зависят от выбранного интегрального критерия эффективности. При синтезе параметрически‑оптимизируемых систем часто используют квадратичные критерии эффективности [4]

Sl=t(e4k) + ^ir^ (4)

где e(k) = q\k)-y(k) – ошибка управления; q^ = Q\k) ; Au(k) = u(k)-u\k) – отклонения управляющего воздействия от оптимального; r – весовой коэффициент (штраф). Выбор весового коэффициента r перераспределяет затраты на управление. Чем больше r , тем меньше изменение u ( k ), тем больше ошибка e ( k ), т.е. система управления становится более инерционной.

Составляющая Δ u ²( k ) определяет затраты на поиск экстремума u ^*( k ), которые включают смещение на один шаг поиска, быстродействие системы и уменьшаются с ростом величины рабочего шага a ( k ) и с уменьшением временных затрат на достижение u ^*( k ^*), где k ^* – шаг, на котором достигнут экстремум.

Составляющая e ²( k ) – определяет потери на рысканье в области экстремума Q ^*( k ).

Также применяют критерии je=t^^                            (5)

4=1

Jk_e=^^.                           (6)

k=l

Эти критерии используют при проектировании как детерминированных, так и стохастических систем.

Для оценки качества процессов управления используем среднеквадратическую ошибку управления на один шаг поиска s.=№lAv-(7)

среднеквадратические отклонения управляющего воздействия на один шаг поиска s.^Oxw,(8)

максимальное перерегулирование

Жп = vmm(^)-^W, либо S^max =^)-llopXk).(9)

k ^* – дискретное время достижения экстремума u ( k ^*).

Для исследований выбраны выпуклые вниз кусочно‑линейная и квадратичная модели, отражающие процесс поиска вдали от экстремума (10) и в области экстремума (11)

Q^(k)) = Q*(k) + Kl\u(k)-u(k)\,(10)

Q^kV = Q\k) + K^u(k^^^(11)

Здесь Q ^*( k ), u ^*( k ) – оптимальное значение целевой функции и управляющего воздействия, K 1 – параметр, определяющий наклон прямых линий, K 2 – параметр, определяющий кривизну функции.

Адаптация параметров регулятора

Адаптация рабочего шага с использованием экстраполятора (Adapt1, Adapt2)

Поскольку структуры модели целевой функции (10), (11) заданы, то можно воспользоваться простыми процедурами оценки их параметров по результатам первых шагов поиска. Полученные оценки параметров позволяют оценить и (k + \) , т.е. спрогнозировать (экстраполировать) следующий (k+1) шаг поиска.

Так, для модели (10) после экспериментов в двух точках u ( k – 1) и u ( k ), используя уравнение прямой, проходящей через три точки [ u ( k – 1), y ( k – 1)], [ u ( k ), y ( k )], [ u ^*( k + 1), Q ^*( k + 1)], определяемой определителем

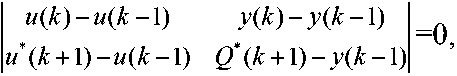
из которого следует

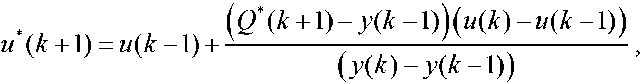
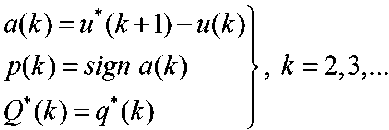
для | y ( k ) – y ( k – 1)| ≥ δ, иначе | a ( k )| = | a ( k – 1)|.

Здесь Q ^*( k ) = q ^*( k ) – известное заранее или предполагаемое, 5 = 0.0Ы(£-1) – уровень порога.

Оценка уровня полезного сигнала на k ‑ом шаге

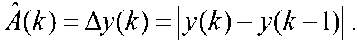
Для кусочно‑линейной функции (10) экстремум u ^*( k ) будет найден на третьем шаге.

Модель (11) раскроем в виде

Q2 ^к)) = \Q\k) + К2и\к)2 ] - 2K7u (к) ■ u(k) + K7 ■ u(k/.

Перепишем (15) в виде

Q7 (w(£)) = b{ + b7u(k) + b3u{k}2.

Для оценки параметров (16) по трем шагам поиска составим систему уравнений bx + b2u(k - 2) + b3u(k - 2)2 = Q(k - 2)

bi+b7u(k-Yj + bji^k-I}2 = Q(k-Y)(17)

bi + b7u(k) + b3u(k}2 - Q(k)

Система уравнений имеет решение, если ее определитель не равен нулю

1 u(k-2) 1 и (к -1) 1 u(k)

и(к - 2)2         и{к -1) • w(^)2 - и(к) ■ н(к -1)2 - и(к-Х)2 =     1/(к — 2)-1Г(к) + /7(к)-1/(к-2)2 +            (18) и(к')2 +и(к - 2) • и(к - 1)2 - и(к - 1) • и(к - 2)2 ^0

В системе (17) значения u ( k ) могут быть не кратны шагу поиска Δ u ( k ), например при переменном шаге поиска.

Если рабочий шаг поиска a ( k ) = a ( k – 1) = a ( k – 2), то выражения (17) и (18) упрощаются и оценки параметров модели (16) на k ‑ом шаге поиска равны

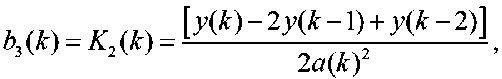
W-^-l.K^

3y(k) ■ a(k) - 4y(k -1) • a(k) + y(k - 2) • a(k) --2y(k) • a(k) + 4y(k - Y)u(k -1) - 2y(k - 2) • utk)

wHew^w]=—

2y(k) ■ a(k^ + у(к) ■ u[kC -

-2y(k -1) • и(к)² + y(k - 2) • u(k)² -

-3y(k) ■ a(k) ■ u(k} + 4y(k -1) • a(k) ■ u(k) -

-y(k - 2) • a{k) ■ u(k)

Для оценки u*(k + 1), продифференцируем уравнение (16)

^fc^ = b^k) + 2b₃ (k)-u(k + l) = O du(k) - 3V 7         7

и найдем

z/(^ + 1) = -4W/(24w),

Q* (£ + !) = b, (k) - b3 (k) • и (к + Г)2.

Для неравных значений a ( k ) последних трех шагов, необходимо использовать оценки параметров b 2 и b 3 из решения системы уравнений (17).

Для равных значений a ( k ) последних трех шагов используем оценки (19), (20).

Значение рабочего шага a ( k ) и направление движения на k ‑ом шаге

a(k) = и (k + l)-u(k),

p(k) = sign (а(кУ).

При достижении области экстремума необходимо уменьшать рабочий шаг a ( k ), например, согласно последовательности

a(k) = a(k -Г)-д1.

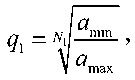
где N 1 – число шагов поиска, за которое рабочий шаг после достижения экстремума уменьшится от a _max до технологически допустимого a _min. При поиске вдали от экстремума с целью уменьшения времени поиска можно увеличивать рабочий шаг

a(k) = а(к-Г)-д2,

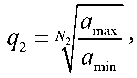
где N 2 – число шагов поиска, за которое рабочий шаг увеличится от a min до a max .

Условием достижения экстремума моделей (10) и (11) можно считать где y(k), Q*(k) – измеренное и прогнозируемое значение выходной переменной ОУ, δ – уровень порога.

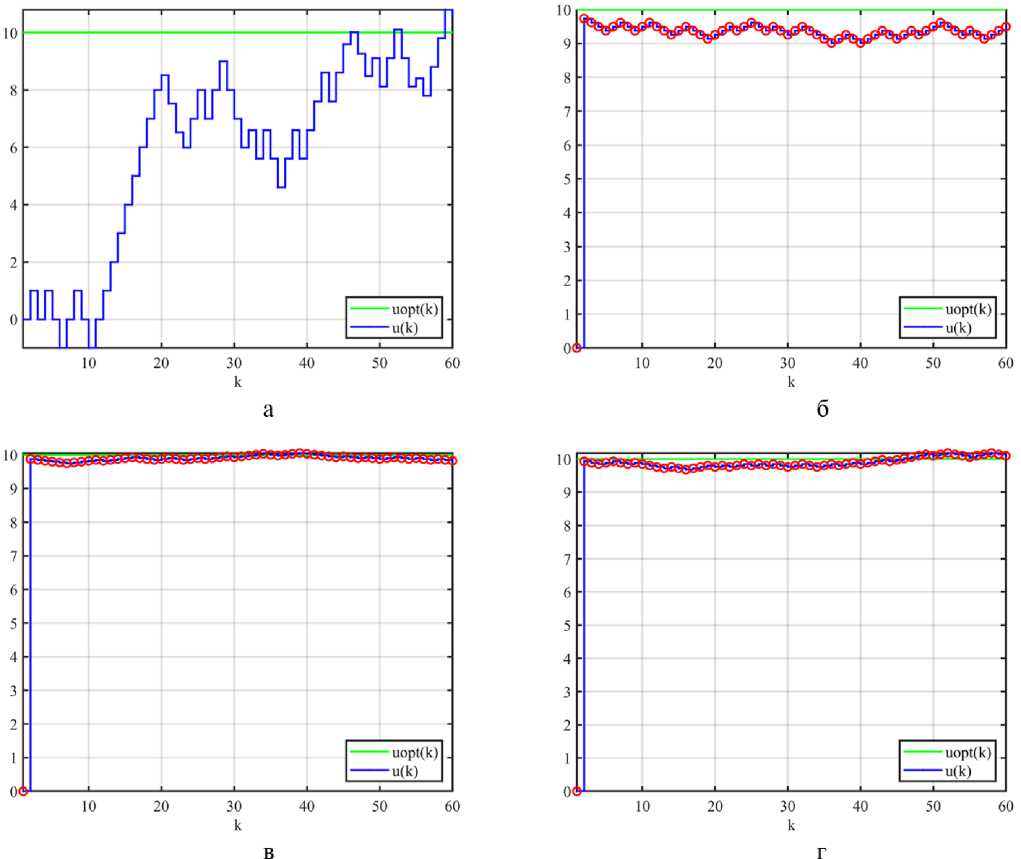
Таким образом, принятием решения о достижении экстремума и, следовательно, уменьшении рабочего шага a(k) является выполнение условия (29), смена направления поиска p(k) – 1106 – на противоположное, иначе увеличиваем a(k) согласно (28), и движемся в том же направлении p(k) = p(k – 1)

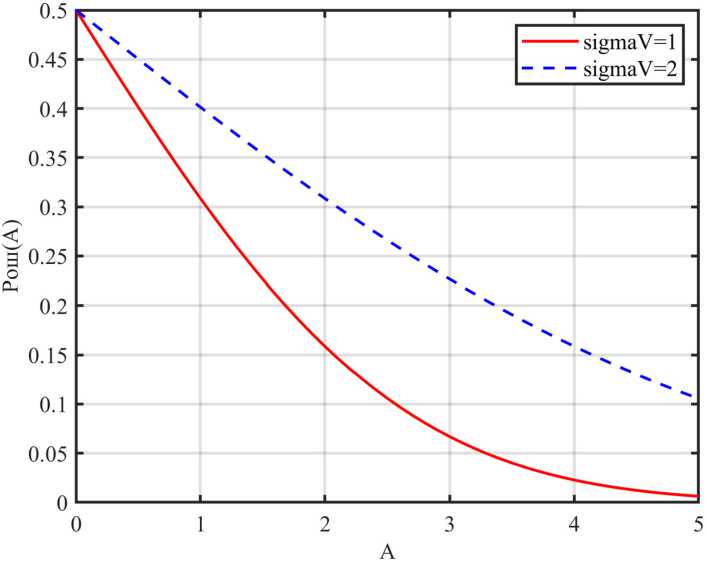
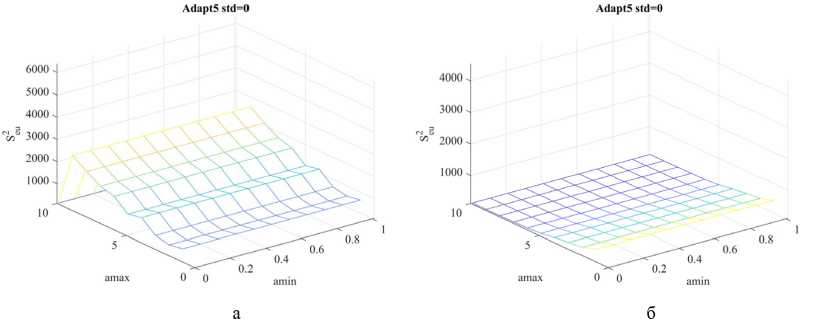
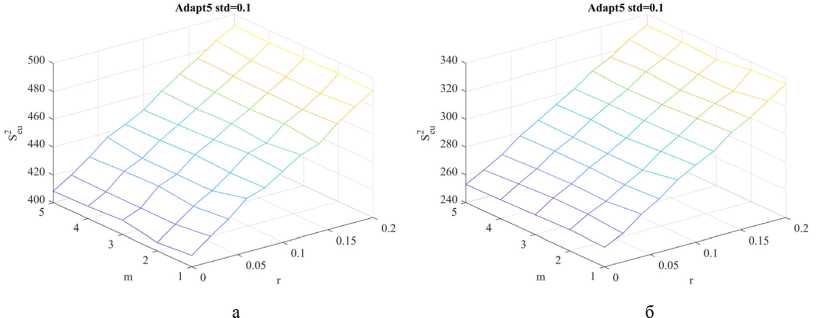
Экстремальное управление в обстановке помех [2]

Пусть помеха V ( k ) имеет математическое ожидание и дисперсию

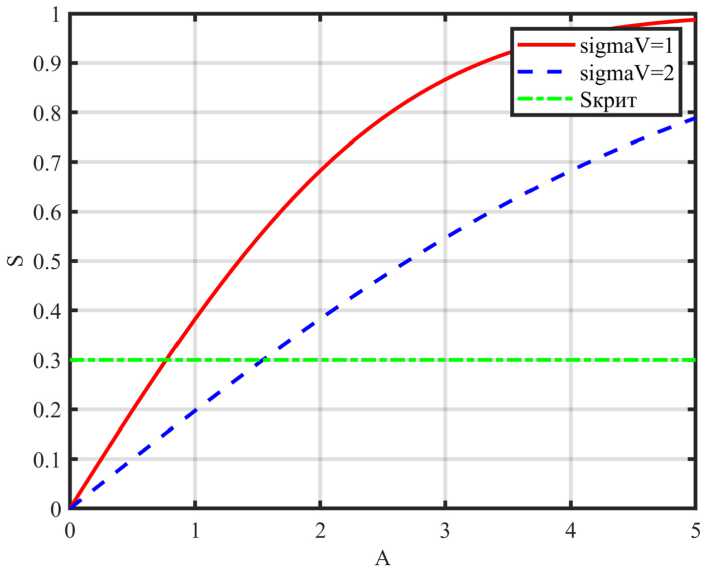
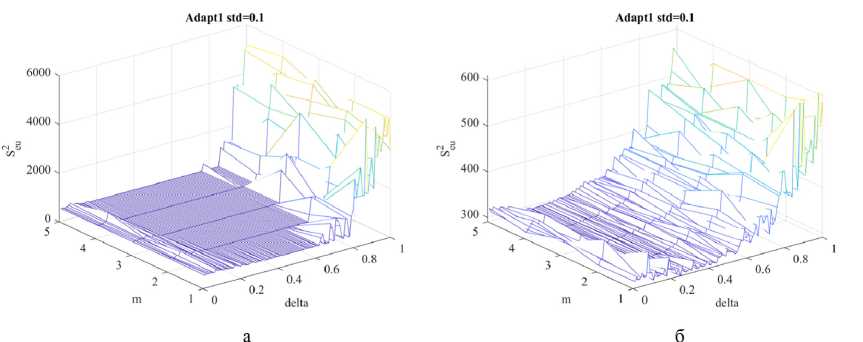
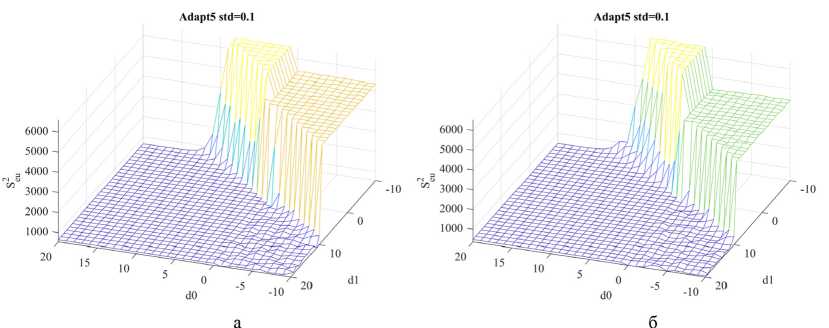
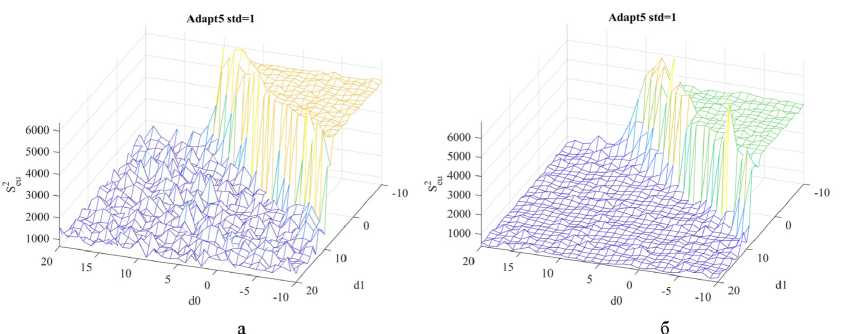
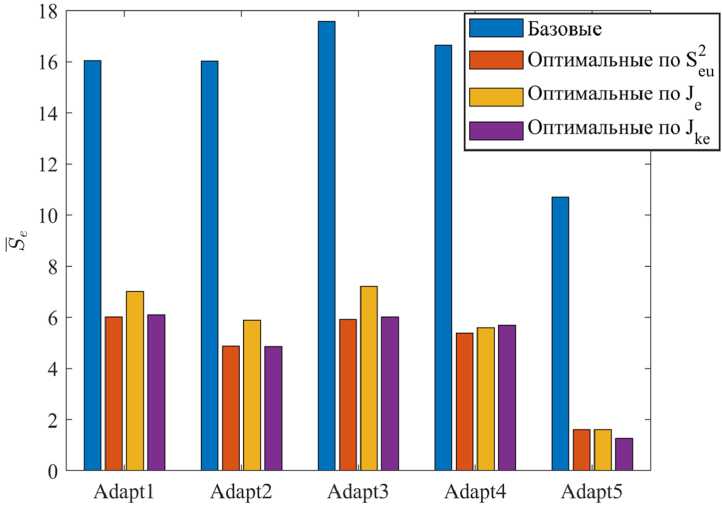
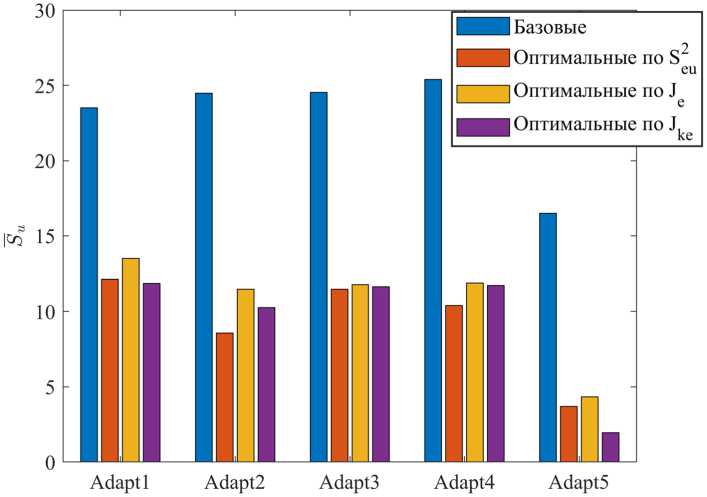
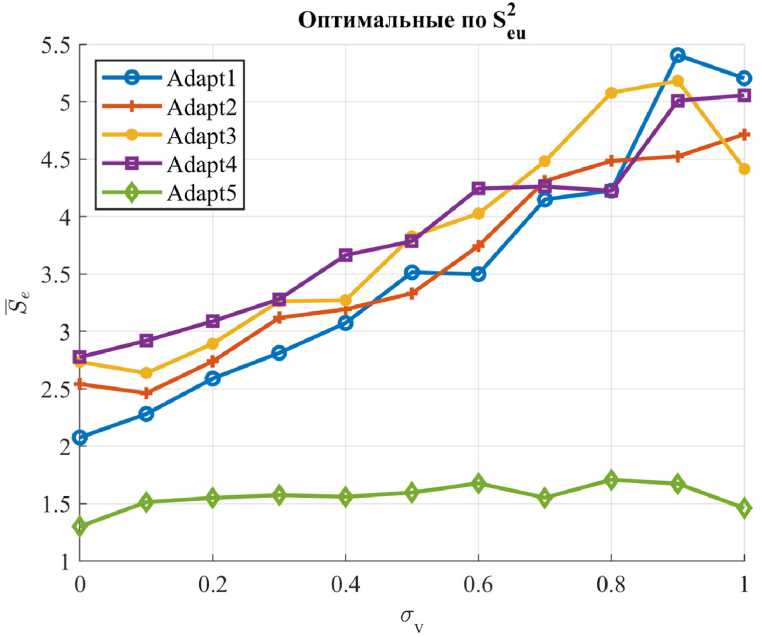
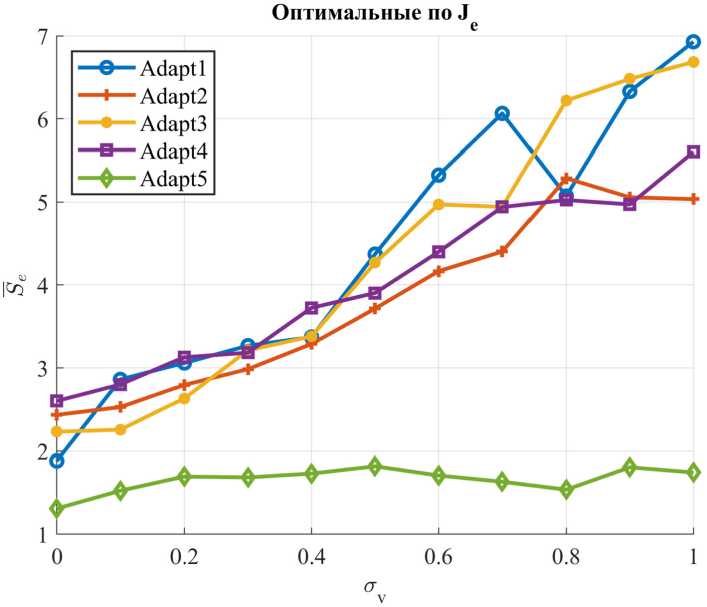
M{V} = mv,D{V} =

Вероятность ошибочного шага [2]

P0lu = Р<Л > ^) • gradQ(u(k})

где ξ = V(k) – V(k – 1), с параметрами M(ξ) = 0, D^^_v.

Для нормального закона распределения помехи V вероятность ошибочного шага равна

независимо от уровня помех.

где Ф(·) – функция Лапласа. Поскольку Ф >0, то всегда

График вероятности (31) ошибки приведен на рис. 2

Среднее смещение к цели u^* определено выражением [2]

8(к) = \а(к)\-Ф

Hw|

2a,.

и приведено на рис. 3.

Для самонастройки параметров СЭУ в условиях помех можно использовать увеличение |A(k)| и уменьшение σV.

Рис. 2. Зависимость вероятности ошибки от уровня полезного сигнала А(k) и уровня помех σ_V = 1 и σ_V = 2

Fig. 2. Dependence of error probability on the useful signal level A(k) and interference levels σV = 1 and σV = 2

– 1107 –

Рис. 3. Среднее смещение к цели в условиях помех

Fig. 3. Mean target displacement under interference conditions

Уменьшение σV можно достичь проведением m повторных измерений на каждом шаге поиска, что позволит уменьшить уровень помехи в 4m раз, но при этом снижается быстродействие поиска на этапе спуска, если учитываем затраты на измерение в критерии эффективности.

Для оценки дисперсии помехи на k‑ом шаге рассчитываем среднее значение (оценку математического ожидания)

и оценку дисперсии помех на каждом шаге, где проводятся повторные измерения, т.е. с учетом результатов предыдущих шагов

где yповт.( j) – значения выхода объекта при повторных измерениях в текущей точке (yповт.(1) = y(k)– первый эксперимент в текущей точке).

Для принятия решения об увеличении числа повторных измерений m необходимо оценить, где находится СЭУ: на этапе спуска или в области экстремума?

Если СЭУ в области экстремума, то выполняется условие (29).

К этому времени выполнено достаточно повторных измерений (k > 10) для оценки дисперсии помехи ^CF и среднего смещения (32).

При низком уровне полезного сигнала, особенно для квадратичной целевой функции (11), и высоком уровне помех введем сглаживание среднего смещения S(k).

где a =       – коэффициент сглаживания; лЫМ – интервал сглаживания.

Для процедур РМНК оценка дисперсии помехи равна остаточной дисперсии, при условии структурной адекватности постулируемой модели объекту.

Если среднее смещение (32)

ад<^ю                                     (36)

и выполняется условие (k > 10), то следует увеличить число повторных экспериментов m = m +

1, но не более m ≤ 5.

Здесь S_крит выбирается априори согласно рис. 3 либо по результатам модельного проектирования.

Использование рекуррентных алгоритмов идентификации (Adapt3, Adapt4)

Для оценки параметров целевой функции Q(u(k)) (1) используем рекуррентные процедуры.

Модель (10) представим в виде

Q (?/(£)) = bx {к} + b, (к) • и (к)

где b^Q^W)– начальная координата, bz (ку – угловой коэффициент.

Для расчета оценки и (кУ на k‑ом шаге поиска при заданном значении q^*(k) необходимо решить систему уравнений пересечения прямой (37) и прямой q^*(u(k)), параллельной оси u(k).

Если q^*(k) известно, то для модели (37) с учетом (12) имеем

и(к + 1) = и(к 1)+⁷⁽^ ^W.                             (38)

b2(k)

Рабочий шаг a^*(k), направление поиска и прогноз Q* (^) согласно (13).

В процессе поиска оценки by (ку и Ь^ (к) будут меняться (уточняться), а в области экстремума они кардинально изменятся (значения и знаки). В этом случае необходимо отключить режим экстраполятора, ограничить рабочий шаг a_min ≤ a_k ≤ a_max и использовать условие (29) для принятия решения.

Модель (11) представим в виде

Q₂ (?/(£)) = b_{(к) + к(к)и(к) + Ь₃ (к)и(к)², где Ш)=й(«(о))– начальная координата.

Соответственно,

2Ь3(к)

а предсказанное значение Q\k + \} согласно (24).

Для вычисления оценок параметров моделей используем РМНК вд = ьц-1)+_®-^Щ—[я*) - ьг<1 -1) ■   ;

1 + X (к) • С(к -1) • х(^) ^{L                      J}

– 1109 – где x(k) – вектор‑столбец наблюдаемых линеаризованных переменных размерности (1 × n = 1), y(k) – наблюденное значение выходной переменной; b(k), b(£-l)– вектор‑столбец оценок параметров модели на текущем и предыдущем шаге поиска, C(k) – ковариационная матрица оценок.

Для модели (10) вектор‑столбец линеаризованных переменных х^М1; wMb                                     (42)

для модели (11)

х(^) = [1; и(к\, i/(k)²^.                                                    (43)

Параметрически- оптимизируемые регуляторы (Adapt 5)

Преобразуем структурную схему одномерной СЭУ (см. рис. 1) к виду, представленному на рис. 4

Рис. 4. Структурная схема СЭУ с управлением по ошибке: УУ – устройство управления; ОУ – объект управления

Fig. 4. Structural diagram of the ECS with error-based control

Здесь q^*(k) – заданное значение выходной переменной в момент времени k, e(k) = q^*(k) – y(k) – ошибка управления.

В качестве регулятора используем дискретный ПИ‑регулятор с передаточной функцией [4]

или разностным уравнением (рекуррентный алгоритм)

u(k) = u(k -1) + p(k) • (J_o • e(k) + d_{ • e(k -1)),

d0 +d{

– коэффициент интегрирования, ^k} = ][q\k)-y(k^

где d0 – коэффициент передачи; ci =------ либо e(k) = [q4k)-y(k)) .         dQ

Выбор направления поиска:

если e(k) – e(k – 1) > 0, то

P(k) = -p(k-l\(46)

т.е. меняем предыдущее направление поиска, иначе

р(к) = р(к-1).

Величина рабочего шага

а(к) = doe(k) + d^k -1).(47)

Настройка параметров регулятора

Задача настройки параметров регулятора («Оптимизатор») реализуется по интегральному критерию

J(^))^min,(48)

где λ – вектор параметров регулятора размерности (n × 1), Λ – допустимое множество значений параметров регуляторалЧ^¹™^,^,™, ^z’=M.

Периодичность настройки параметров регулятора определяется технологическим циклом и динамикой их изменения. Решение может приниматься в ходе технологического процесса по мере увеличения величины интегрального критерия (48) на фиксированном интервале эксплуатации, например минуты, часы, дни и т.д. Если процесс стабильный, то, возможно, достаточно однократной настройки. Если условия в ОУ изменяются с периодом, то по итогам предыдущего периода осуществляют настройку параметров регулятора на следующий цикл.

Задача (48) многомерная. Учитывая нелинейность и стохастичность ОУ, а соответственно, и функции J(e(k)), следует использовать метод нулевого порядка, последовательный симплексный метод (ПСМ), генетический алгоритм и другие.

Таким образом, в СЭУ действует параллельно два контура адаптации (рис. 5), первый Adapt(·) корректирует параметры рабочего шага a(k) регулятора на каждом шаге поиска. Второй – «Оптимизатор», корректирует параметры процедур Adapt(·) по одному из критериев (4), (5), (6) на периоде, кратном первому контуру f 0, при Д£(/) < Nn

7 = 7к Mf\^M                                  (49)

приД^(7)>^,, где Δkj = k(j) – k(j – 1); Nn – шаг оптимизации контура «Оптимизатор».

Выбор границ допустимого множества параметров Λ

Корректный выбор позиционных и функциональных ограничений допустимого множества Λ во многом определяет затраты времени на решение и реализацию задачи (48) (время поиска, учет технологических ограничений, методы оптимизации и т.п.). Моделирование СЭУ для различных интегральных критериев и моделей объекта управления Q(k) реализо-– 1111 –

Рис. 5. Структурная схема самоорганизующейся дискретной СЭУ с адаптерами и «Оптимизатором»

Fig. 5. Structural diagram of a self‑organizing discrete ECS with adapters and an “Optimizer”

вано для относительных единиц, что позволяет перейти к реальным границам и параметрам множества Λ.

Для выявления допустимых границ множества параметров Λ построим поверхности зависимости интегрального критерия (4) от следующих пар параметров СЭУ: {N1, N2}, {amin, amax}, {d0, d1}, {Sкрит, r}, {δ, m}.

Исходные данные для исследования. Параметры модели (10): K1 = 1, u^*(k) = 10, Q^*(k) = 0. Начальные условия: p(1) = 1, u(1) = 0, a(1) = a_max, N = 60.

Параметры модели (11): K2 = 0.1, u^*(k) = 10, Q^*(k) = 0. Начальные условия: p(1) = 1, u(1) = 0, a(1) = a_max, N = 60. Исходные (базовые) и граничные значения параметров адаптивных регуляторов, Adapt1 ÷ Adapt4 приведены в табл. 1, для экстремального ПИ‑регулятора (Adapt5) в табл. 2.

Для процедуры адаптации шага с линейным экстраполятором (Adapt1) получены следующие поверхности (рис. 6–9):

Анализ представленных поверхностей отражает наличие эффективных зон параметров, схожих по характеру для обеих моделей, но отличных по значению функции 8ей . Квадратичная модель имеет меньшие значения функции ^ ей . Влияние пары {δ, m} (рис. 9) существенно для квадратичной модели в условиях помех. Увеличение параметра r функции (рис. 8) увеличивает потери на рысканье и уменьшает затраты на управление. При отсутствии помех (std=0) параметр Sкрит не влияет на S_gu .

Для процедуры адаптации шага с квадратичным экстраполятором (Adapt2), с использованием РМНК (Adapt3) и (Adapt4) поверхности функций 8ей имеют схожий вид.

Для экстремального ПИ‑регулятора (Adapt5) поверхности функции ^ ей представлены на рис. 10–13.

Согласно рис. 10 и 11 области эффективных значений параметров {d₀, d₁} определяют «плато», в том числе в условиях помех. На этом «плато» система не критична к соотношению – 1112 –

Рис. 6. Поверхность критерия Sей от {N₁, N₂} при σ_V = 0 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Fig. 6. Criterion $ ей surface vs {N₁, N₂} at σ_V = 0 for: а) piecewise‑linear model; б) quadratic model

Рис. 7. Поверхность критерия $ ей от {a_min, a_max} при σ_V = 0 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Fig. 7. Criterion 8ей surface vs {a_min, a_max} at σ_V = 0 for: а) piecewise‑linear model; б) quadratic model

Рис. 8. Поверхность критерия ^ ей от {Sкрит, r} при σV = 0 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Fig. 8. Criterion ^ей surface vs {S_крит, r} at σ_V = 0 for: а) piecewise‑linear model; б) quadratic model

Fig. 9. Поверхность критерия Sей от {δ, m} при σV = 0 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Fig. 9. Criterion ^eu surface vs {δ, m} at σV = 0 for: а) piecewise‑linear model; б) quadratic model

Рис. 10. Поверхность критерия ^ей от {d₀, d₁} при σ_V = 0.1 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Fig. 10. Criterion ^ей surface vs. {d₀, d₁} at σ_V = 0.1 for: а) piecewise‑linear model; б) quadratic model

Рис. 11. Поверхность критерия ^ей от {d0, d1}при σV = 1 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Fig. 11. Criterion ^ей surface vs. {d0, d1} at σV = 1 for: а) piecewise‑linear model; б) quadratic model параметров {d0, d1} в пределах допустимой области. Отметим, что допустимые области изменения параметров классического ПИ‑регулятора и экстремального существенно отличаются.

Влияние параметров рабочего шага (рис. 12) отражает рост потерь на поиск при росте amax для кусочно‑линейной модели, и незначительно влияние amin и amax для квадратичной модели. Влияние штрафа r на управление (рис. 13) на функцию S^ существенно для обеих моделей и подтверждает, что чем больше r, тем меньше изменение u(k), тем больше ошибка e(k). Влияние же числа повторных измерений при малом уровне помех незначительно.

Полученные рисунки позволяют определить зависимость интегрального критерия эффективности управления S^ от параметров регулятора, выделить недопустимые зоны параметров и степень их влияния.

Рис. 12. Поверхность критерия ^ей от {a_min, a_max} при σ_V = 0 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Fig. 12. Criterion ^ей surface vs. {a_min, a_max} at σ_V = 0 for: а) piecewise‑linear model; б) quadratic model

Рис. 13. Поверхность критерия S^ от {r, m} при σ_V = 0.1 для: а) – кусочно‑линейной модели; б) – квадратичной модели

Рис. 13. Criterion S^ surface vs. {r, m} at σ_V = 0.1 for: а) piecewise‑linear model; б) quadratic model

Поиск оптимальных значений параметров регуляторов

Поиск произведен по интегральным критериям ^ей (4), Je (5), Jke (6). Качество процессов управления спроектированных оптимальных регуляторов оценивалось по критериям S_e (7), S_u (8). Для решения задачи (48) использован глобальный алгоритм нулевого порядка – генетический алгоритм. Оптимизация проведена на квадратичной модели (11) с исходными данными и параметрами при построении поверхностей функции Sей, для уровня помех σV = 1. Результаты исследования приведены в табл. 3–5.

Исследование проводилось на квадратичной модели, в которой соотношение уровня полезного сигнала A(k) к уровню помех σV равно

или

A(k} |2-0.L«(4(»^-10)| I \    \ M

—J------- у ⁷----= 0.2 ■|«(4 (w (k) -10)|

Таблица 1. Параметры для исследования адаптивных алгоритмов Adapt1÷Adapt4

Table 1. Parameters for the study of adaptive algorithms Adapt1÷Adapt4

Параметр	Базовые значения	Ограничения
N1	1	1 ≤ N1 ≤ 15
N2	1	1 ≤ N2 ≤ 30
amin	0.1	0.01 ≤ amin ≤ 1
amax	1	1 ≤ amax ≤ 30
δ	0.01	0.01 ≤ δ ≤ 1
m	2	1 ≤ m ≤ 5
крит	0.3	0.1 ≤ Sкрит ≤ 0.5
r	0.1	0 ≤ r ≤ 0.2

Таблица 2. Параметры для исследования экстремального ПИ‑регулятора (Adapt5)

Table 2. Parameters for the study of the extremal PI‑controller (Adapt5)

Параметр	Базовые значения	Ограничения
amin	0.1	0.01 ≤ amin ≤ 1
amax	1	1 ≤ amax ≤ 10
m	2	1 ≤ m ≤ 5
крит	0.3	0.1 ≤ Sкрит ≤ 0.5
r	0.1	0 ≤ r ≤ 0.2
d0	1	–10 ≤ d0 ≤ 20
d1	1	–10 ≤ d1 ≤ 20

Таблица 3. Оптимальные по ^ ей значения параметров регуляторов

Table 3. ^ ей ‑optimal parameter values of the regulators

Параметр	Adapt1	Adapt2	Adapt3	Adapt4	Adapt5
N1	2	2	6	2	-
N2	22	26	26	27	-
amin	0.24	0.57	0.32	0.56	0.12
amax	4.67	4.76	4.44	4.54	9.74
δ	0.07	0.08	0.08	0.08	-
крит	0.39	0.32	0.46	0.31	0.20
m	2	5	5	4	5
r	8.2*10–4	42*10–4	47*10–4	22*10–4	35*10–4
d0	-	-	-		‑7.65
d1	-	-	-		-5.44

Таблица 4. Оптимальные по Je значения параметров регуляторов

Table 4. J_e‑optimal parameter values of the regulators

Параметр	Adapt1	Adapt2	Adapt3	Adapt4	Adapt5
N1	2	2	2	3	-
N2	30	25	25	12	-
amin	0.27	0.15	0.19	0.37	0.02
amax	4.35	4.01	4.18	4.37	9.88
δ	0.06	0.03	0.05	0.05	-
крит	0.46	0.27	0.17	0.33	0.32
m	5	3	5	5	5
r	-	-	-	-	-
d0	-	-	-	-	‑0.47
d1	-	-	-	-	-8.84

Критерии эффективности (4), (5), (6) отражают потери на поиск при движении к экстремуму и в области экстремума (потери на рысканье [2]). Согласно (50) доля потерь на поиск выше потерь на рысканье. Для их уменьшения необходимо быстро достичь области экстремума и быстро уменьшить рабочий шаг amax до amin. Полученные соотношения amin, amax и N1, N2 отражают эту стратегию.

Уровень пороговой фильтрации δ, критическое среднее смещение к цели Sкрит синхронизируются с уровнем полезного сигнала в области экстремума и минимизируют потери на рысканье.

Влияние штрафа r в критерии (4) оказалось не столь значительным по причине быстрого перехода в область экстремума (1–2 шага).

Для сравнения эффективности полученных оптимальных параметров регуляторов (табл. 3–5) между собой с базовыми значениями (табл. 1–2) выбрана квадратичная модель и условия при поиске оптимальных параметров регуляторов.

Таблица 5. Оптимальные по J_ke значения параметров регуляторов

Table 5. J_ke‑optimal parameter values of the regulators

Параметр	Adapt1	Adapt2	Adapt3	Adapt4	Adapt5
N1	5	2	2	3	-
N2	29	28	28	22	-
amin	0.21	0.26	0.47	0.39	0.04
amax	4.61	4.64	4.29	4.37	9.93
δ	0.04	0.08	0.09	0.07	-
Sкрит	0.25	0.29	0.39	0.19	0.49
m	5	5	4	5	5
r	-	-	-	-	-
d0	-	-	-	-	‑5.73
d1	-	-	-	-	‑8.43

Поскольку эксперименты проводились в условиях помех, то сравнение качества процессов управления проводилось по среднему значению критериев (7) S_e и (8) S_u для серии испытаний L = 100.

На рис. 14 и 15 видно, что оптимальные параметры значительно улучшают качество процессов управления у всех регуляторов по критериям S_g и S_u по сравнению с базовыми параметрами. По результатам оптимизации наилучший результат показал экстремальный ПИ‑регулятор (Adapt5).

В целом критерии (51), (52) схожи по влиянию базовых и оптимальных параметров на качество процессов управления. Конечно, если выбрать другие базовые параметры, различие можно уменьшить, но их сложно подобрать в 6‑мерном пространстве параметров на интуитивном уровне.

Различия между оптимальными адаптивными регуляторами обусловлено их структурой. Так, Adapt1 и Adapt3 ориентированы на линейную аппроксимацию целевой функции, а Adapt2 и Adapt4 на квадратичную аппроксимацию на каждом шаге поиска.

Экстремальный ПИ‑регулятор (Adapt5) наилучший по критерию J_ke в обоих случаях. Влияние уровня помех на качество процессов управления для оптимальных регуляторов по критерию (51) на квадратичной модели (11) приведено на рис. 16–18.

На рисунках видно, что минимальные значения критерия (51) имеет экстремальный ПИ‑регулятор (Adapt5) на всем диапазоне уровня помехи σ_V, для критериев эффективности ^ ей , Je, Jke, а регуляторы с РМНК предпочтительнее экстраполяторов.

На рис. 19 показаны процессы управления для рассмотренных наборов параметров экстремального ПИ‑ регулятора при уровне помех σV = 1 на квадратичной модели (11).

Параметры экстремального ПИ‑регулятора по критерию J_e (см. рис. 19в) обеспечивают наилучшее качество процессов управления.

Рис. 14. Качество процессов управления для базовых и оптимальных параметров по критерию S_g

Fig. 14. The quality of control processes corresponding to the baseline and optimal parameters, as evaluated by the s criterion

Рис. 15. Качество процессов управления для базовых и оптимальных параметров по критерию S_u

Fig. 15. The quality of control processes corresponding to the baseline and optimal parameters, as evaluated by the s criterion

Выводы

Предложенный в работе подход для синтеза параметров дискретных экстремальных регуляторов позволяет целенаправленно выбрать интегральные критерии эффективности в зависимости от свойств объекта управления и возможностей устройства управления как априори, так и в процессе управления. Система экстремального управления позволяет оценивать качество процессов управления. В совокупности она позволяет менять не только параметры регулятора, но и структуру регулятора из имеющегося набора, то есть «самоорганизации».

Рис. 16. Влияние уровня помех на качество процессов управления для оптимальных регуляторов по критерию ^еи

Fig. 16. The influence of the noise level on the quality of control processes for regulators optimal in terms of the s criterion

Рис. 17. Влияние уровня помех на качество процессов управления для оптимальных регуляторов по критерию Je

Fig. 17. The influence of the noise level on the quality of control processes for regulators optimal in terms of the Je criterion

Оптимальные пп .Т

О            0.2           0.4           0.6           0.8            1

ст V

Рис. 18. Влияние уровня помех на качество процессов управления для оптимальных регуляторов по критерию Jke

Рис. 18. The influence of the noise level on the quality of control processes for regulators optimal in terms of the Jke criterion

Рис. 19. Графики процесса управления для а) базовых параметров; б) оптимальных по ^еи; в) оптимальных по J_e; г) оптимальных по J_ke

Fig. 19. Control process plots for: а) baseline parameters; б) ^еи‑optimal; в) Je‑optimal; г) Jke‑optimal

Наиболее перспективным в задачах экстремального управления представляется экстремальный ПИ‑регулятор. В работе найдены области эффективных значений его параметров d0, d₁, он прост в реализации и обеспечивает высокое качество процессов управления, в том числе в условиях помех.