Модельные представления опытного производства самолетов

ет каждое название (уникальное имя, идентификатор) с отношением R n из сигнатуры Q отношение rⁿ соответствует местности.

Выбор той или иной модели для представления рассматриваемых объектов производства и исследования структуры их связей определяется свойствами этих объектов, которые выражаются признаками (атрибутами) объектов. Признаки, характеризующие свойства объектов, могут быть непрерывными и дискретными, количественными и качественными, либо смешанными.

Обычно совокупность объектов представляется множеством точек в некотором многомерном (как правило, метрическом) пространстве, оси которого соотносятся с соответствующими признаками. В прикладных задачах в качестве такого пространства достаточно часто (но, заметим, не всегда обоснованно) выбирается пространство типа евклидового Eⁿc метриками d En [1] при различных значениях n, выраженными формулами

Е 1 = (R,dE1) с метрикой

dEi(x,y) = A(x - y)2 = lx - y|,     (2)

E2 = (R2,dE2) с метрикой

• dE2(x,y) = 7(Х1 - У1)2 + (Х2 - У2)2 , (3) En = (Rn,dEn) с метрикой Евклида

n

• ^dEn^(x, y) = _A Е ^(xi ^- yJ 2 .       (4)

i=1

Задание расстояния между объектами позволяет оценивать близость или удаленность этих объектов относительно друг друга вне зависимости от их природы, исследовать структурные особенности совокупности объектов и всего пространства в целом.

В проблемах многокритериального принятия решений, распознавания образов, классифика- ции и других предметных областях рассматриваются совокупности объектов A ={A1, …, Ak}, которые описываются m дискретными признаками Q1,...,Qm, имеющими конечное число es e =1,…, h , s=1,…, m количественных (число-qs ,s ,…, s,       ,…, вых) или качественных (номинальных, либо порядковых) значений. Порядковые значения качественного признака Qs обычно предполагаются упорядоченными от лучшего значения к худшем qS ^ q2 ^ ... ^ qhs . Каждый объект из A, i=1, …, k из совокупности A можно представить как точку qi, в m-мерном векторном пространстве Q = Q1 XQ2 X... XQ являющемся прямым произведением шкал значений признаков QS, и поставить объекту Ai в соответствие m-мерный вектор

Qi = (QMb-^em)-      (5)

Ситуация существенным образом усложняется, если одному и тому же объекту А_i , может соответствовать не один, а несколько m -мерных векторов с различающимися значениями признаков [1, 2].

В рамках теоретико-множественных представлений, как членения самолета, так и состава его сборочных частей (СЧ) и сборочных единиц (СЕ) представляют собой обычное множество U={x₁, x₂, …, x_n}, все элементы x_i которого различны для различных СЕ и самолетов в целом. Однако в рамках опытного производства запланировано изготовление пяти опытных образцов (ОО) для различных видов испытания. Этот факт фиксируется в создаваемой автором единой теории представлений объектов производства (ОП) путем введения мультимножества или множества с повторяющимися элементами, как и обычное множество, есть совокупность элементов произвольной природы. Однако в отличие от множеств, один и тот же элемент может присутствовать в мультимножестве многократно, и кратность вхождения элемента является существенной особенностью, делающей мультимножество качественно новым математическим понятием. Элементы множеств и мультимножеств будем обозначать строчными буквами а, b , ..., множества - прописными буквами А, В ,..., мультимножества - прописными полужирными буквами А , В , …, семейства множеств и мультимножеств – рукописными буквами A , B ,..., системы множеств и мультимножеств — прямыми буквами А, В, ... [3].

С точки зрения формализации ОП (конструкции самолета; схема членения планера самолета, сборочных единиц, сборочных частей и т.д.) мультимножеством А, порожденным основным (обычным) множеством U={x1, x2, …}, все элементы конструкций (ЭК) ОП (самолета и его частей) хi, которого различны, называется сово- купность групп одинаковых элементов конструкций самолета и его частей.

^A = ^{k A 1 *^Х 1 , ^k A 2 •^X 2 ^,-^}, ^X i £ U. ⁽⁶⁾

Группу одинаковых будем называть элементов k _{A 1}•x₁ будем называть компонентой мультимножества, одинаковые элементы x_i, входящие в компоненту k _{A 1}•x₁ – экземплярами элементов мультимножества, а функцию k _A , значение которой k _A (x₁)=k _{A 1}, определяет число вхождении элемента x i ^ U в мультимножество А или “вес” элемента х_i в мультимножестве А – функцией кратности или функцией числа экземпляров мультимножества А . Таким образом, мультимножество – это множество, состоящее из различных групп одинаковых экземпляров ЭК.

Характеристика принадлежности ЭК к мультимножеству А некоторой конструкции определяется функцией кратности

• , > 0 — целое, если х Е А,

k A (x)= (7)

Наряду с функцией кратности k _A введем характеристическую функцию _А мультимножества А , которая принимает значения

_А (х)= (8)

Эти функции задают соответственно отображения: k A :U ^ Z + и % _А :U ^ Z 01 . Множество U служит областью определения функций k A и % А , а множества Z₊и Z₀₁ – соответственно областями значений.

Так как мультимножества семейства A ={ A₁ , A ₂,…} в нашем случае образуются из одного и того же множества G ={x₁, x₂,…}, то множество G называется порождающим множеством ЭК ОП или доменов для семейства A . В дальнейшем будем считать, что мультимножества порождены одним и тем же доменом.

В компактной форме мультимножество ЭК ОП в рамках систем опытного производства (СОП) записывается в символическом виде следующим образом:

A _i={k _{A i}(x₁)•x₁,…, k _{A i}(x_h)• x_h}, (9) определив элементы множества G ={x₁,…, x_h} следующим образом:

• ^Х1 = Q^{1 ,x}2 = Q^{2 ,} ... ^,xh₁ = Q h^1,xh_{1 +} 1 = Q 2 ,... ^,xh_{1 +} h₂ = Q h^2, ...^,₍₁₀₎ ^xh_{1 +} ... ₊ h_m _ _{1 +} i = Q m ,... ^,xh_{1 +} ...h m = Q h m ^,h = ^h1 + ... + ^hm .

Множество G определяет свойства совокупности объектов A ={A-1,…,Ak} и множеством их признаков G={x1,…, xh}, выраженные с помощью матрицы С=||cij||k•h, которая использована для представления конструкций серийных образцов (СО), а использование операций, объединения, пересечения, арифметического сложения, арифметического вычитания, дополнения, симметрической разности, умножения на число, арифме- тического умножения и возведения в арифметическую степень, прямого произведения и возведения в прямую степень позволяет провести системно-информационный анализ конструкций, с одной стороны для научно обоснованного группирования сборочных единиц по методам сборки с учетом наличия сборочной оснастки, способам базирования, и с другой – структурных свойствах самолета как объекта производства [3].

Например, группы X _t объектов, классификация и типизация которых осуществлена на базе основных характеристик: опорного множества или носителя мультимножества A _t, состоящее из единичных экземпляров всех элементов, входящих в эти мультимножества

SuppA={x|x=G, ^Supp a (x)= %a (x);(1

мощность мультимножества А определяется как общее число экземпляров всех его элементов

|A|=cardA = ^ka (x) ,(12)

xeG а размерность мультимножества А – как общее число различных элементов

/A/ =dimA = УхA (x).(13)

x e G

Группы Xt объектов, представленных мультимножествами Аi, могут быть получены как суммы Xt= ^Ai , объединение Xt= ЦАi, или пере-ieI t                                                               iel t сечение Xt= ^Ai мультимножеств, описывающих объекты Ai. Тогда совокупность Xt объектов характеризуется матрицей С’=||ctj’||, ctj’=kt’(xj), имеющей соответственно следующие элементы kt(x)= Eki(x),kt(xj)= maxk,(xj),kt(xj)= mink<(xj). (14) iel                                            iel iel,                                                        1                                                         '

Носитель мультимножества является подмножеством порождающего множества G (Supp A G ). Мощность носителя равна размерности мультимножества |Supp A |=/ A / и не превосходит мощности домена |Supp A |<| G |. Очевидно, что разные мультимножества могут иметь один и тот же носитель.

Очень важным для формализации агрегатно-сборочного производства является введение отношения включено, так некоторая сборка, представленная мультимножеством В содержится или включено в мультимножество А (В А), если kB-(x) kA(х), для каждого элемента x G. Мультимножество В называется тогда подмультимножеством мультимножества А, а мультимножество А – надмультимиожеством мультимножества В. В этом случае /В/ |A|, /В/ /A/, hgtB < hgtA, SuppBS SuppA, a xA. = xB., либо x A. ^ xB.. Как и в случае обычных множеств, од- новременное выполнение условий B A и A влечет мультимножеств А=В.

В рамках введенных отношений и операций над мультимножествами и проводившихся автором исследований, относящихся к классификации конструкции самолетов как ОП (агрегатов, отсеков, секций, панелей и т.д.), привели его к задаче выяснения тех методологических средств, которые необходимы для формирования непере-секающихся классов ОП различных уровней, используемых для построения и сравнения различных сборочных единиц из составных частей, агрегатов, секций, панелей и самолета из них, будем в дальнейшем называть образующими конструкций и самолета в целом. Множество образующих будем обозначать в соответствии с введенными выше обозначениями для мультимножеств: А , а для его отдельных элементов а , а А .

На различных этапах анализа образующие ОП представляются лишь как неделимые целостности, как наличные в среде проекта носители своих свойств, они для нашего анализа будут двух типов: признаки и связи.

Первый тип свойств – признаки в качестве его значений для конкретной, могут выступать целые числа, действительные числа, векторы, тензоры и т.д. Второй тип свойств охватывает связи, необходимые для включения образующей в сложные конструкции.

С системных позиций следующим шагом в детализации представлений об ОП является декомпозиция средств, в которых он рассматривается. Целостный ОП в среде одного уровня рассматривается как структурная единица целостности, например, панель, а в другой, например в среде этого ОП (панели), в которой будут обнаружены различающиеся по своим признакам и связям новые объекты (например, обшивка, продольный и поперечный набор составных частей), то есть объекты в объектах (ОП в ОП), которые характеризуются своими признаками.

Для решения задач глубокой классификации ОП с целью построения СОП введем понятие «наблюдение», которое в рамках многократного наблюдения ОП, как ОП в ОП привело к системному выводу о необходимости различать в целостности две такие противоположности, как часть и целое, и о возможности в целом выделять части с их границами, не нарушая целостности. Условием осуществления этой процедуры оказывается осмысление того факта, что частям целого присущи не только качества и границы, но еще и связи, то есть нарушения границ. Целостность целого оказывается, в различных условиях его нахождения, конкретной разновидностью такой целостности, которая выражает связность частей, и тогда сохранность границ целого осознается как следствие нарушения границ частей.

Таким образом, введенные системные, теоретико-множественные понятия, позволяющие описывать целостность различного уровня (агрегат, отсек, секция, панель и т.д.) в виде связности. Центральным звеном в понимании связности является связь. Связи ОП нередко необходимо рассматривать не просто как сумму особых компонентов, а в их непосредственной роли: как связующие компоненты, конкретным образом расположенные между образующими. Каждой определенной образующей соответствует число соединений, связывающих данную образующую с остальными. Каждому соединению соответствует показатели связи В .

Множество связей всякой образующей а , соответствующим образом перенумерованное, образует структуру связей образующей. Структура связей не определяет значения показателей, поставленных в соответствие отдельным связям.

Связность ОП выражается, как уже отмечалось, в том, что его элементы включены в сеть связей друг с другом. Будем называть схему сети связей между образующими ОП структурой этого ОП. В этом случае будем говорить не о составе, а о сети связей объекта, обеспечивающей связность.

Факты контактирования связей через посредничество образующих – соединителей, будет рассматриваться как точка, представляющая собой узел связей в структуре.

Для решения комплекса задач агрегатно-сборочного производства введено понятие формального описания ОП, которые обладают внутренней структурой и могут в рамках их декомпозиции расщепляться на компоненты. Объекты, являющиеся на некотором уровне формального описания изображениями, считать образующими в формализме более высокого уровня. Независимо от того, работаем ли мы с подобной иерархической структурой или нет, на любом уровне образующая будет рассматриваться как непроизводный элемент.

Таким образом, предложенные формы описания ОП позволяют осуществить переход от реального объекта к формальному описанию, которое может быть реализовано с разной степенью точности, что, в свою очередь, приводит к описаниям разного типа, которые широко используются для решения задач 1-го этапа: постановку задачи проектирования опытного производства конкретного самолета, разработку концептуальной модели предметной области. Предлагаемая модель ПО, как и знаковая модель любого ОП, представляется базовыми множествами, введенными выше, и набором заданных на них отношений. Базовые множества модели отображают классы, подклассы и типы объектов, выделяемых в ПО, в соответствии с классификацией ОП, которые объединены в множества всех образующих, состоящее из непересекающихся классов образующих А б, А6 с A, где б - общий индекс, индекс класса образующих А= ЦАа, А6 – непересекающиеся классы.

Интерпретация этого разбиения состоит в том, что образующие, сходные качественно, будут отнесены к одному классу. Образующие базовых множеств описывают отдельные ОП каждого данного класса, подкласса, типа, представляя их как целостности — носители свойств в среде и на фоне своей структуры. Поскольку состав и значения существенных признаков любого ОП могут быть конкретизированы только для точно определенных состояний среды (внешних и окрестностных условий объекта), описание объектов должно включать описание присущего им окружения — элементарных фрагментов предметной области (ПО), структура которых представлена на рис. 1.

Отношения, входящие в состав концептуальной модели ПО, должны отображать реально существующие отношения между ОП: различных классов, подклассов, типов (род – вид, целое – часть, вид – род, часть – целое, соподчинения и др.); одного класса, подкласса, типа (тождества, принадлежности и др.).

Отношения между ОП и средой (внешними и окрестностными его условиями) подлежат отображению в описании каждого элементарного фрагмента ПО.

Рассматривая объекты различных классов в аспекте их жизненного цикла, выделим в окрест-ностных условиях их среды основные, “взаимодействующие с каждым объектом, системы: использующую, изготавливающую, проектирующую, исследующую, информирующую. Любой объект есть некоторая целостность, которая состоит из отдельных компонентов или элементов, рассматриваемых как подобъекты по отношению к объекту или сообъекты — объекты равного уровня сущности по отношению друг к другу. При этом объект по отношению к своим компонентам выступает в качестве окрестностных условий их среды. В этой связи желательно, чтобы состояния любых объектов ПО, рассматриваемых самостоятельно или в качестве компонентов других объектов, отображались посредством единой, типовой модели-описания. За основу построения такой типовой модели берется образующая ПО.

Необходимая степень полноты и детализации отображения ПО достигается посредством предлагаемого подхода только потому, что спектр задач НТПП затрагивает ограниченную и точно

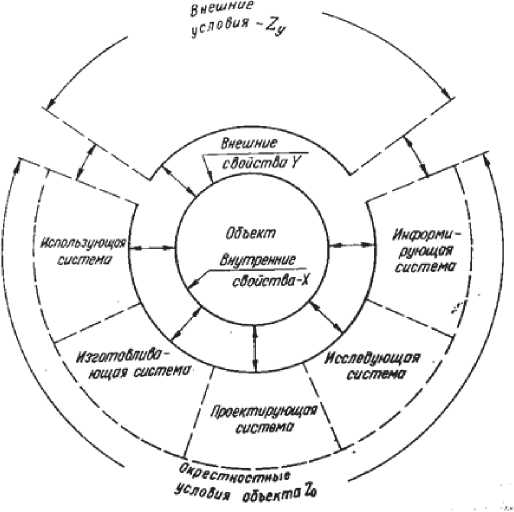
Рис. 1. Модель-описание типового фрагмента предметной области.

Среда Z=Z Z .

yo известную часть отношений, существующих между входящими в состав ПО объектами.

При сравнительном анализе конструкций на основе концептуальной модели, который выполняется для формирования перечня конструкторско-технологических проблем создания самолетов данного класса, в частности, анализ СО (В) и ОО (А) позволил в рамках одноименности (гомогенности) их конструкций ( А В ), если их носители совпадают (Supp А =Supp В ) и существует взаимно однозначное соответствие f между одноименными компонентами: k _B (х)=f(k _А (х)) для каждого элемента x G; разноименно (гетерогенно) или D-эквивалентными ( А В ), если их носители эквивалентны (Supp А ~Supp В ) и существует взаимно однозначное соответствие f между разноименными компонентами: k _B (х_i)=f(k _А (х_j)), x_i,x_j G где f – целочисленная функция с областью значений Z ₊. S- и D-эквивалентные мультимножества равноразмерны / B / =/ A /, их высоты связаны равенством hgt В =f(hgb A ), установить факторы снижающие и повышающие трудоемкость ОО по сравнению с СО, а также осуществить классификацию и типизацию ОП.

Предложенная методология и теория представления ОП позволяет в процессе системноинформационного анализа реального проекта самолета РПС в рамках сохранения структурных единиц целостности (СЕЦ), на которые расчленен самолет и которые взаимоопределены, взаимообусловлены и существуют лишь в соотнесении друг с другом, в контексте представления об их целостном единстве, установить связь между исследуемыми объектами будущего производства и их моделями, которая отображается следующей схемой:

R ₁                    R ₂

РПС(ОП)_пр ^ М(ОН) и о М [М(ОП)_и], (12) где РПС(ОП)_пр – реальный проект самолета (РПС); М(ОП)_и – идеализированный, направленно-упрощенный, гипотетический образ РПС – модель, определенная средствами языка мультимножеств, в границах которой рассматривается объект, сформированный для достижения точно определенных, конкретных целей (именно в этой связи данная модель должна удовлетворять критерию практики), на основе ряда аксиом и теорем, всегда неполного по составу, а также тезауруса предметной области, к которой данный объект относится, или в среде объектов которой рассматривается; М [М(О)_и] —знаковая, логикоматематическая, символическая, наглядно-образная модель идеализированного образа РПС; R₁ – отношение, имеющее характер гомоморфизма (направленное упрощение РПС, выражающееся в выделении и отображении лишь некоторых сторон структуры, лишь части свойств и отношений между свойствами объекта); R₂— отношение, которое может быть гомоморфным и даже изоморфным.

Схема связи между объектами РПС и его моделями имеет вид:       _R 0

{М [М(ОП)_и]} ^ РПС(ОП).     (13)

Основные отношения, которые наиболее важны для проектирования любых объектов, в том числе агрегатов РПС, и соответственно для предметной интерпретации получаемых результатов, – это отношения R : o

РПС(ОП)рп^ {М [М(ОП)и]}, где Ro – морфизмы неопределенной и непостоянной категории. В общем случае Ro – отношения, отображающие лишь факт сомоделируемости соотносимых объектов РПС(ОП)рп и {М [М(ОП)и]}.

В соответствии с приведенной формальной процедурой решаются проблемы классификации ОП, необходимая для технологической подготовки их производства (ТПП), получения полного набора образующих для построения образа технологического процесса (ТП) их изготовления, сравнения образов ОП и самолетов, распределения работ ТПП между станочным оборудованием и расчета трудоемкости реализации того или иного ТП с учетом состава операций соединения агрегатов, отсеков, секций, панелей на основе ис- пользования теоретико-множественных операций, позволяет с высокой достоверностью определить трудоемкость.