Модельные решения уравнения четвертого порядка со смешанной производной

Описание процесса колебаний упругого полотна является важной задачей в математике и в других разнообразных областях науки и техники, включая электродинамику, гидродинамику, аэродинамику, акустику, строительную инженерию и другие науки, а также инженерные дисциплины.

При исследовании модельной задачи о движении упругого полотна возникают различные вопросы и подзадачи. Одна из главных особенностей связана с тем, что дифференциальное уравнение в частных производных, описывающее процесс колебания упругого полотна, является уравнением четвертого порядка. Также в нем присутствует слагаемое со смешанной производной, что не дает применить классический метод разделения переменных (метод Фурье).

Решение подобного класса задач способствует анализу динамики деформации и процессов колебания упругого полотна. Далее возникает необходимость учета множества факторов, которые влияют на моделирование процесса в целом, например, стоит учитывать скорость распространения колебаний в полотне, чтобы при движении полотно не подвергалось чересчур сильным колебаниям.

Исследования в области колебаний движущихся материалов и конструкций остаются актуальными и важными в современной науке. Наблюдается постоянный прогресс и рост интереса к этой теме. За последние годы было проведено множество исследований, которые позволили получить более глубокие знания в данной области науки. Например, в работе [1] автором рассматривается модельная задача одномерных малых поперечных колебаний полотна. В существующей литературе уже представлены результаты по соответствующим модельным задачам. Однако данная работа представляет оригинальный подход получения решений и универсальный подход к решению задач данного класса.

Просмотреть подробно нахождение решений для уравнения балки и ознакомиться с рядом интересных вопросов по данной теме можно в работе [2]. Авторы рассматривают в качестве уравнения четвертого порядка в одномерном случае поперечные колебания тонкой балки. В работе [3] автор исследует анализ и управление поперечными колебаниями движущихся струн, которые движутся вдоль оси. Проводится анализ линейных и не- линейных динамик струны и рассматривается влияние параметров струны. В работе имеются аналитические выкладки, численные симуляции и экспериментальные результаты.

Исследования поперечных колебаний с временно зависимой скоростью движения представлены в работе [4], где авторы исследуют вопрос о существовании и устойчивости стационарных режимов колебаний струны при временно зависимой скорости движения. Также работа включает анализ переходных процессов.

В работе [5] рассматриваются поперечные колебания нити с постоянной скоростью. Наиболее важная проблема, которую рассматривают авторы, связана с возникновением резонансных эффектов при поперечных колебаниях нити.

Для понимания математических методов и техники вычислений, которые будут проведены, можно обратиться к трудам [6–8], в которых рассматриваются различные разделы математики.

В работе [9] рассматривается вибрационное поведение пластин, состоящих из функционально-градиентных материалов при различных начальных и краевых условиях. Изучение влияния таких материалов является важной задачей.

Такие материалы, как полотно, движущееся с постоянной скоростью, подвержены разрушениям. Известно, что в процессе производства в бумажном полотне могут возникать различного рода дефекты, такие как вздутия, срезы волокон и вздутия по краям. В работе [10] авторами представлены важные результаты по данной теме, такие, как вопросы об устойчивости, разрешении, долговечности, представлены значения дифференциальных операторов, построены численные алгоритмы, проведен анализ колебаний.

Рассмотренные вибрационные поведения движущихся балок Тимошенко в работе [11] при различных краевых условиях помогают изучить влияние краевых условий на вибрационное поведение движущейся балки, что является хорошим подспорьем для разработки новых эффективных структур.

Для решения выдвинутой задачи требуется внимательно изучить метод Галёркина, который является важным инструментом при поиске решения уравнения колебаний упругого полотна. Суть его заключается в создании сходного базиса с использованием вспомогательной задачи, что значительно упрощает поиск решения исходной.

Метод Галёркина представляет собой мощный инструмент для нахождения базиса при решении дифференциальных уравнений высокого порядка, таких как уравнения четвертого порядка. Этот метод позволяет аппроксимировать сложные функции базисом известных функций, что упрощает решение уравнений.

Процесс применения метода Галёркина начинается с выбора базисных функций, которые могут представлять решения уравнения. Затем уравнение четвертого порядка представляется в виде скалярного произведения между ним и каждой из базисных функций. Далее это произведение интегрируют по области, где выполняется анализ, и приравнивают интегралы к нулю.

Этот процесс создает систему алгебраических уравнений, в которой неизвестными являются коэффициенты базисных функций. Решая эту систему, можно найти эти коэффициенты и, следовательно, базис функций. Этот базис затем используется для аппроксимации и анализа решения дифференциального уравнения четвертого порядка.

Метод Галёркина широко применяется в численных методах для решения сложных уравнений и позволяет значительно упростить процесс анализа и вычисления. Подробнее о приближениях Галёркина и самом методе написано в [12], где автором подробно рассмотрен данный метод и приведены конкретные примеры.

Модельные решения уравнения четвертого порядка со смешанной производной

Как и в работе [1], будем рассматривать следующее уравнение:

22 D

H--и =0.# tt 0tx 0xx xxxx .

m

Но теперь, внося условие о том, что v 0 = c , исходное уравнение будет иметь другой вид, для которого будут отысканы точные решения далее.

Это условие дает возможность посмотреть на движение упругого полотна, скорость движения которого равна скорости распространения колебаний в нем.

Итак, теперь накладывая данное условие на изначальное уравнение (1), получаем новый вид уравнения:

u tt + ² v 0 u tx + ^Duxxx_x = °.#                               ⁽²⁾

m

Пусть T, l eK+ . Пусть далее ^(П) - является пространством функций, которые будут определены на множестве П = [0; l ]х [0; T ], удовлетворяющих краевым условиям:

ui = u I = ui = u I = 0,# xx               xx

I x=0 X=0 x=l x=l а также имеющих производные до 4-го порядка включительно по переменной x и до 2-го порядка включительно по переменной t . На данном пространстве функций введем дифференциальный оператор L :

т d'        a²     d a⁴ .

L: —2" + 2 v 0 —2—2" +---4.# dt2      dx2dt2 m dx4

Тогда уравнение (2) может быть представлено в таком виде:

Lu = 0.#

Чтобы в дальнейшем кратко выписать теорему единственности, необходимо будет воспользоваться интегральным соотношением. Чтобы его представить, для начала стоит определить скалярное произведение (и,а). Пусть и,®е ^(П). Тогда получим:

( и , a ) JJ v-a dxdt .

Лемма 1. Пусть и , ® е ^ ( П ) . Далее пусть оператор L определен формулой (4). Тогда выводим:

t l 1                                       D 1

( L u , a ) =     I ( uj)-u^)_t - 2 v 0^+—x^xx^x x fat .

0 0 ^ t                     m J

Доказательство. Для доказательства данной леммы будем искать скалярное произведение ( L u , a ) :

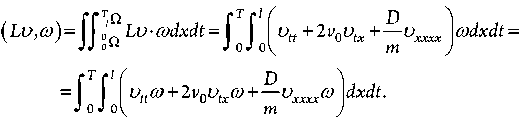
Далее, пользуясь формулой для интегрирования по частям и равенством ( u t a ) t = u tt a + и, 01, , получаем то же соотношение, что было в лемме.

Воспользовавшись выведенной ранее леммой 1, установим закон сохранения энергии. Для начала нужно обозначить и = u , а a = u_t , u - функция из формулы (5). Применив данные замены для скалярного произведения ( L u , a ) , а также проделав несложные вычисления, легко заметить, что:

0 = (Lu,ut) =            | ut +uxx |dxdt.#(6)

• 2 о о d t к

Далее из формулы (6) получим l (

0 к

• 2 D 2 ^ t = T ,„ .

ut +—uxx I. _ndx = 0.# m J t = 0

Пусть далее имеются следующие соотношения:

u t ² = k ( ^x , t ) , Du² x = p ( ^x , t ) . ^m

Тогда, подставив в форму (7) данные соотношения и раскрыв пределы интегрирова- ния, имеем

J ( k ( x , T ) + p ( x , T ) - ( k ( x ,0 ) + p ( x ,0 ) ) ) dx = 0.#                     (8)

Пусть E ( t ) - полная энергия движущегося полотна в момент времени t, которая определяется следующей формулой:

l

Е ( t ) = ( k ( x , t ) + p ( x , t ) ) dx .#                               (9)

Посмотрев на формулы (8) и (9), несложно увидеть, что Е ( T ) = Е ( 0 ) . Сформулируем полученный результат в виде леммы.

Лемма 2. Пусть Е ( t ) - полная энергия движущегося полотна, которая определена формулой (9). Тогда данная энергия сохраняется, а именно V T >  0 имеет место равенство Е ( T ) = Е ( 0 ) .

Далее, воспользовавшись законом сохранения энергии, несложно получить теорему единственности.

Теорема. Пусть u1 и u2 – два решения начально-краевой задачи (2)-(3). Тогда u1 - и 2 = 0.

Доказательство . Пусть и = и 1 - и ₂. Эта функция является решением уравнения (2), удовлетворяет краевым условиям (3) и нулевым начальным условиям:

U = 0, и = 0.#                               (10)

Это означает, что в начальный момент времени энергия равна нулю. В силу закона сохранения энергии (лемма 2) в произвольный момент времени энергия также будет нулевой. Из этого следует, что V 1 1 >  0

Е( 11) = Е( 0 ) = 0, и ut = 0 и —uxx = 0 для всех точек [0; l]. Отсюда получаем, что и = const. m

В силу начальных условий (10) имеем и = 0, что и следовало доказать.

Методология исследования

Из-за того что в уравнении появляется смешанная производная, явно не удается применить обыкновенный метод решения дифференциальных уравнений, такой как метод разделения переменных Фурье. Поэтому для поиска точных решений будет применяться новый метод решения подобных уравнений.

Метод заключается в следующем. Сначала необходимо определить, в каком виде будем искать решение. Для этого этапа необходимым является отыскание схожего базиса решений вспомогательного уравнения. Здесь пригодится метод Галеркина.

Модельные решения уравнения четвертого порядка со смешанной производной

Далее, определив данную функцию, подставляем ее в исходное уравнение и получаем вид уравнения с замененной функцией.

После всевозможных математических упрощений получаем обыкновенное дифференциальное уравнение. Применяем стандартный метод решения дифференциальных уравнений. Составляем характеристическое уравнение, находим корни этого уравнения.

Выводим решения для определенной ранее функции и проводим обратную замену, получаем окончательный вид решения исходного уравнения.

После того как перешли к решению задачи с начальными и краевыми условиями, необходимо найти базис из экспоненциальных функций и выполнить разложение по этому базису.

Из начальных условий можем определить коэффициенты. В данной статье на основе нескольких примеров можно увидеть применение вышеперечисленного метода.

Нахождение решения уравнения

Для метода Галеркина необходимо найти вид (представление) собственных функций в другом базисе, в другой задаче. Начать необходимо со вспомогательной задачи.

Имеем следующую задачу о колебании балки

U tt + a ² u xxxx = 0.#                                      (11)

со следующими условиями закрепления и начальными условиями:

Ui = u I = u \ = u I = 0, x       xx xxx

^U t = ₀ = f ^{( x} ) , ^U t[ ₀= g ^{( x} ) .

В ходе решения при использовании метода Фурье разделения переменных получаются следующие собственные функции:

X ( x ) = C ■ cos ( 41A x ) + D ■ sin ( 4fA x ) + A ■ ch ( 4/A x ) + B ■ sh ( 4 J x ) .#             (12)

Отходя в сторону, надо рассказать про сам метод Фурье. Суть метода разделения переменных заключается в следующем.

• 1.    Исходное дифференциальное уравнение разделяется на уравнения, зависящие от отдельных переменных.

• 2.    Предполагается, что решение может быть представлено в виде произведения функций от раздельных переменных: u ( x, t ) = X ( x ) T ( t ) .

• 3.    Подставляем такое решение в исходное уравнение, оно, в свою очередь, разделяется на уравнения, зависящие только от одной переменной.

• 4.    Уравнения решаются по отдельности, и ищутся решения.

• 5.    Произведение этих функций будет являться решением исходного уравнения.

Возвратимся к задаче. Далее, воспользовавшись данными начальными условиями, а именно X(0) = X(0) = X(l) = X(l) = 0, составим систему:

| A ( ch ( 4 ^1 ) + cos ( 4/Л 1 ) ) + B ( sh ( 4 % l ) + sin ( 4/ ! l ) ) = 0;

| A ( sh ( 4/A l ) - sin ( 4/A l ) ) + B ( ch ( 4/A l ) + cos ( 4/A l ) ) = 0.

Однородная система имеет решение относительно неизвестных A и B тогда и только тогда, когда ее определитель равняется нулю, то есть:

ch ( 4 Л 1 ) + cos ( 4j A l ) sh ( 4/ A l ) + sin ( 4/ A l ) sh ( 4/ d l ) - sin ( 4/ A l ) ch ( 4 Л 1 ) + cos ( 4 Л 1 )

= 0.#

Из уравнения (13) получается алгебраическое уравнение для вычисления собствен- ных значений задачи:

ch2 (4/Л1) + 2 ch2 (4/Л1) cos (4/Л1) + cos2 (4[Al) = sh 2 (4Л1)- sin2 (4jAl ).#

Далее, обозначив и=4/Al и воспользовавшись равенством sh2 (x) + 1 = ch2 (x), из уравнения (14) найдем ch (и )■ cos (и ) = -1.#

Приближения для и можно искать при помощи алгоритма Ньютона - итерационного численного метода для поиска корней (нулей) заданной функции:

F ( Ис )

Ис +1 = Нс-

^{F (} И к )

= -        ^ch ( Ис ) ■ ^cos ( Ис ) + ¹

^{Н к +} 1 ^{И к sh} ( И к ) ^cos ( Ис ) ^{- ch} ( Ис ) ^sin ( Ис ) .

Также можно решить уравнение (15) графически (на Рисунке 1 изображен такой график).

Корни уравнения (15):

И = 1,875, И 2 = 4,694, ^ , И г ~ ~ ( 2 n — 1 ) ^пры n >  3.

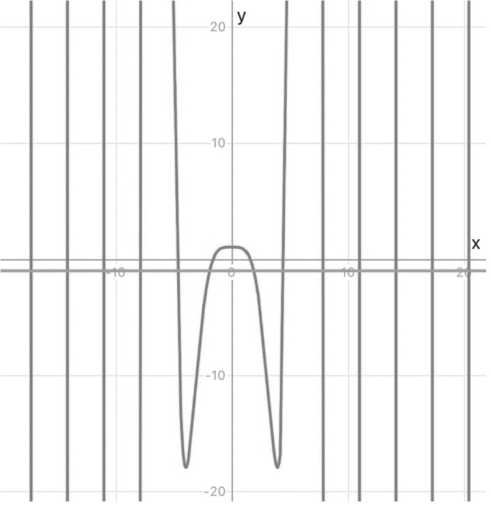
Рисунок 1. Определение корней уравнения ch ( и ) ■ cos ( и ) = — 1 Источник: здесь и далее рисунки выполнены авторами.

Модельные решения уравнения четвертого порядка со смешанной производной

После решения окончательно получаем вид функции u ( x , t ) для вспомогательной задачи:

где

I     А  ,1. I    A     I

u„ ( x , t ) = A„cos\ a—r-t \ + B„sm\ a—^t \ X„ ( x ) , n '     ' n I      1 2 I ⁿ I      1 2    / n\'

^X n ⁽ x ^{) =}

( ^sh ( A n )

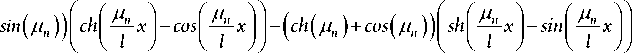
^sh ( A n ) + sin ( A n )

После разбора вспомогательного примера можно перейти к отысканию решений основной задачи, используя полученный вид на собственные функции разобранной задачи.

Итак, в основной задаче зададим v 0 = c , и получим вид

D

u tt + ² v 0 u tx +    u xxxx = °.#

m

Решение уравнения (16) ищется в виде u ( x , t ) = T ( t ) e ^ ^x , где Л берется из вспомогательной задачи, а именно

X n ( x ) =

( ^sh ( A n )

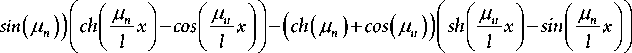
^sh ( A n ) ^{+ sin} ( A n )

следовательно, решение выглядит так:

u(x,t) = T(t)e4^"x , а так как i - An4 Лп= -T

что может быть представлено как

A n l

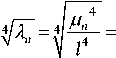
A n —

l

An_i '

l

- ^ni то решение для T(t) получается следующим образом:

T ( t ) =

e

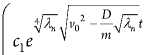
⁺ c 2 e

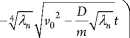
Окончательный вид решения ^

N u ( x, t ) = ^^ n = 1

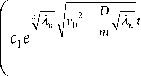
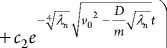
e ^ ( x - v 0 t )

Далее для поиска точных решений и определения коэффициентов необходимо воспользоваться методом, описанным в [1].

Имеем уравнение (2) с начальными и краевыми условиями:

u = u I = ui = u I = 0,# xx               xx

I x =0

I x =п          x =п

u

1 1 = 0 = ^{f (} x ) , 4 = ₀ = 0^.

Разобьем поиск точных решений и отыскание коэффициентов на две части, где в первой части f ( x ) = sin ^—— x ^ , а во второй части f ( x ) = ch ^—— x ^ . Решением будет являться сумма отдельных решений.

Первая часть отыскания точного решения.

Используя формулу Эйлера, получаем f (x) = sin( —x | = —

I l 7 2 i

ix e^l

—

--ix el

.

Так как 4j ^ 1 = —iи4 2 2 = — —i , то получаем следующую систему для поиска коэффициентов:

u

— ix

I t = 0 = ( C _n + C 2! ) e l  + ( C ₁₂ + C 22 ) e

—      — ix             ix l = - el

2 i

--e

2 i

— --x

l

< ^u t

1 1 =0

(

—

C 11

\ ^v 0 ⁺

^{D —}

m

^— v 0

—

—

C 21    i

( I2ГЧ

I 2 ^{D —}

X V 0 +--y

\ ml ²

— ix e l +

+

—

^— C ¹² T '

\

\ 2 , D —

\ v 0 ⁺-- 27 ^— v 0

m l

—

^{+ C} 22 ~'

I 2 , D — \ v 0 ⁺ - ТГ \ m l

⁷ 7

^— --ix e ^l = 0.

\ 2 , D — ²

Пусть v0 +---— = у , тогда, решив систему, можно записать окончательное решение m l2

первой части в виде

— u ( x, t )=2

# .

V

Вторая часть отыскания точного решения.

Используя известное соотношение для гиперболического косинуса и его связи с экспонентой, получаем

f ( x ) = ch\ — x | =—

I l 7 2

( —

x el + e

I

— ^ x

■ l

Так как 4/23= —, а4/Л4 = — —, то получаем следующую систему для поиска коэффици- ентов:

Модельные решения уравнения четвертого порядка со смешанной производной x                 - x 1 x 1 - ult =0 =( C11 + C 21 ) el  + ( C12 + C 22 ) e l  = 2i el  - Ti e l

1 u t

t = 0

^C 11

E l

(

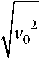
D e ² ml ²

-

v ₀

^C 21

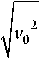
D E 2 ml ²

E x e^l

+

^{- C} 12

e

l

(

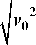
D E 2

ml ²

-

v ₀

, E „ 2 ⁺ C 22 i  ]l^v 0

D e ²

ml ²

⁺ v 0

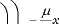
^{+ v} о e

= 0.

Пусть

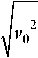
D e 2

--Y = ? т тогда, решив систему, можем записать окончательное решение m l ²

первой части в виде и (x, t ) = —

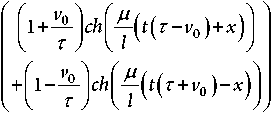
Далее, проверим полученное решение (20) на единственность, воспользовавшись формулой (8), отыщем производные по аргументам решения (20) и возведем в квадрат для того, чтобы получить необходимые соотношения:

u t = k ( x , t ) , Du xx = p ( ^x , t ) .

m

Проделав необходимые, довольно громоздкие вычисления, нетрудно прийти к выводу о том, что для того чтобы формула (8) обращалась в нуль, необходимым условием стано- вится следующее равенство:

т = v ₀, где = = . V o ₀ ²

—

D e 2 m l 2 .

D e 2

Данное равенство возможно лишь в случае, когда    2 обращается в нуль, а такое не- ml возможно, так как ни переменная ц E , ни жесткость D не могут равняться нулю.

Следовательно, получаем вывод о том, что решение (20) не обращает формулу (8) в нуль, а отсюда следует, что теорема единственности не выполняется. Можем откинуть в сторону данное решение.

Получив необходимые точные решения и откинув второе решение, которое не подошло из соображений единственности, можно записать общее решение целиком, которое состоит только из слагаемого (19):

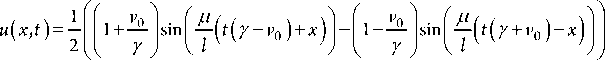
Можно перейти к самой иллюстрации решения на графике для следующих начальных коэффициентов: l = 2, v ₀ = c = 30, m = 500, D = 100. И в моменты времени времени t = 0; 0,1; 0,3; 0,5. В качестве краевых условий были взяты краевые условия (18). Можно наблюдать моделирование динамики изменений колебаний решения обозначенной задачи на Рисунках 2–5.

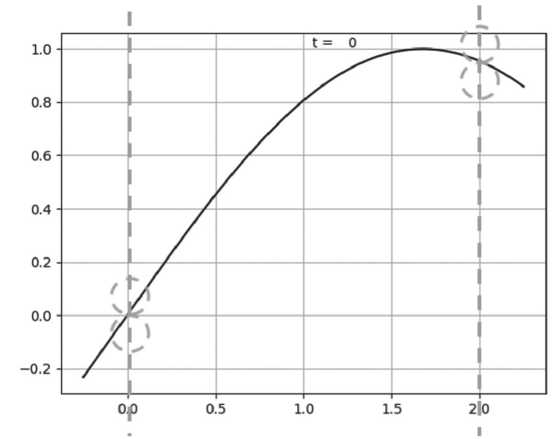
Рисунок 2. График решения в момент времени t = 0

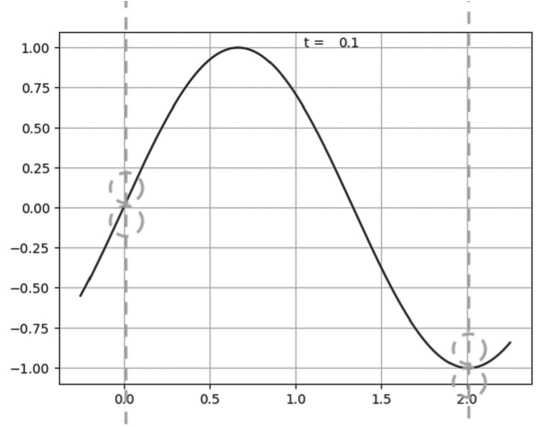
Рисунок 3. График решения в момент времени t = 0,1

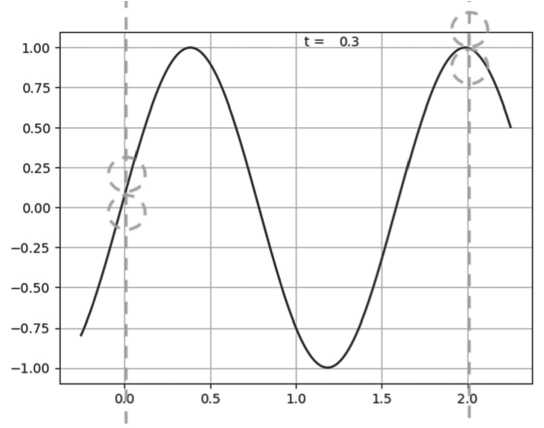
Рисунок 4. График решения в момент времени t = 0,3

Модельные решения уравнения четвертого порядка со смешанной производной

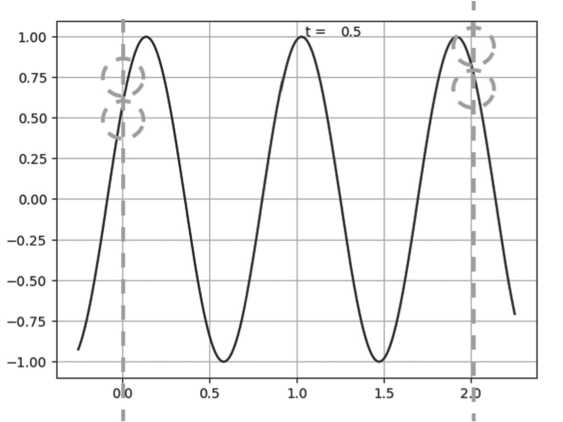
Рисунок 5. График решения в момент времени t = 0,5

Моделирование динамики колебаний решаемой задачи позволяет исследовать влияние различных параметров на процесс колебания полотна. Например, можно изучить и оценить то, как изменение жесткости или массы полотна влияет на его колебания. Моделирование позволяет не только воспроизвести экспериментальные результаты, но и исследовать различные параметры, которые могут в той или иной степени повлиять на колебания движущегося упругого полотна.

Результаты исследования

Результаты исследования указывают на то, что движущееся упругое полотно проявляет разного рода волновые режимы. Так, при постоянной скорости движения наблюдаемого объекта видно то, как за ним и перед ним образуются похожие волны, также можно наблюдать распространение волн вдоль объекта.

Меняя различные параметры в описанной задаче, такие как скорость, жесткость и вес, мы наблюдаем, что динамика колебаний такого упругого полотна сильно зависит от данных параметров. В частности, увеличение параметра, отвечающего за жесткость или уменьшение веса полотна, приводит к увеличению скорости распространения волн и частоты колебаний.

Из демонстрации динамики колебаний с течением времени можно наблюдать возникновение осцилляций, то есть повторяющегося движения или колебания полотна вокруг некоторой равновесной точки или положения равновесия. Они характеризуются периодичностью, амплитудой и частотой (см. Рисунок 5).

Моделирование этих процессов подтверждает вышеуказанные утверждения. Было обнаружено, что смоделированные решения уравнения могут точно воспроизводить экспериментальные результаты, что позволяет использовать модель для дальнейшего изучения колебаний движущегося упругого полотна с условиями закрепления шарнирного типа.

Обсуждение результатов

О результатах исследования можно сказать то, что, используя данный новый метод нахождения точных решений для указанной задачи, а именно для задачи о колебании движущегося упругого полотна, можно более точно предсказать и анализировать поведение упругого полотна с течением времени.

Это открывает новые возможности для разработки более эффективных, надежных и устойчивых конструкций, а также для оптимизации процессов производства.

Таким образом, результаты исследования движущегося упругого полотна имеют огромный потенциал для применения в различных областях, включая инженерию, механику, строительство и др. Они позволяют расширить знания о поведении упругих материалов и способствуют развитию новых технологий и материалов.

Как видно по результатам проведенных исследований, колебания движущегося упругого полотна являются сложным явлением, которое зависит от многих параметров. Однако, получив новый метод, удалось описать эти колебания.

Заключение

В работе рассмотрены поперечные колебания движущегося упругого полотна. В качестве математической модели, описывающей этот процесс, рассмотрена начально краевая задача для уравнения 4-го порядка со смешанной производной с постоянными коэффициентами. Для представленных задач с выдвинутыми условиями закрепления и поставленными начальными условиями, специального вида, получены семейства точных решений. Приведено решение для начальной функции, представленной в виде гиперболического косинуса.

Также была выполнена подробная визуализация решения соответствующей краевой задачи на Рисунках 2–5 в разные моменты времени.