Models of quantum intelligent control pt.1: evolution of control systems based on quauntum feedback

Control system theory, and in particular feedback control systems, is an important aspect of modern engineering. It provides a set of tools for the design of technology with reliable performance and has been applied with overwhelming success in the design of many of the devices that we use on a daily basis. The engineering and control of devices at the quantum-mechanical level — such as those consisting of small numbers of atoms and photons — is a delicate business. The fundamental uncertainty that is inherently present at this scale manifests itself in the unavoidable presence of noise, making this a novel field of application for stochastic estimation and control theory.

Remark. Processes in the micro-world transpire according to laws and principles that directly contradict those governing the macro-world of human experience. This radical shift in understanding is now almost a century old and definitively confirmed by many experiments. It might seem likely that the strange behaviors of quantum systems would be familiar by now, and practical devices harnessing those behaviors would be commonplace. For the most part, however, we have remained mere spectators of the microphysical realm where quantum mechanics holds sway, observing naturally occurring phenomena rather than being able to control and manipulate them. The impressive degree of engineered control exhibited in macroscopic systems such as jet aircraft and the Internet is far from being demonstrated. Indeed, the development of quantum technologies for utilizing microscopic processes has lagged far behind our ability to observe and understand them [1-35].

That lag may be reversed in the coming decade. Recent advances in quantum and atomic optics and condensed matter physics are providing tools to engineer practical quantum devices and perhaps even modestly complex networks of these devices. The discovery of inherently quantum computational algorithms that can outperform certain known classical methods is providing added incentive to develop these devices. Quantum information processing, precision measurements and the development of ultra-sensitive sensors are driving the present development of quantum technologies. If quantum technologies are ever to achieve the complexity of classically engineered systems, the development of a theory of quantum feedback control

Электронный журнал «Системный анализ в науке и образовании» Выпуск №1, 2018 год becomes essential, since feedback control is at the heart of the stability and predictable behavior of complex engineered systems.

Along these lines, recent theoretical results on error correction in quantum computing and on the dynamics of open quantum systems may be viewed as first steps in developing a theoretical formalism for practical quantum feedback control. Indeed, feedback control represents a promising new approach to mitigating quantum noise and decoherence in both quantum computing and precision measurement. If we are to apply feedback control theory concepts and methods to quantum dynamical systems, we must not only extend classical control concepts to new regimes but also analyze quantum measurement in a way that is useful for control systems. Nanoscale science and technology, often spoken of as “nanoscience” or “nanotechnology,” are simply science and engineering carried out on the nanometer scale, that is, 10 ^{- 9} meters. Figure 1 provides some sense of how this scale relates to more familiar, everyday scales.

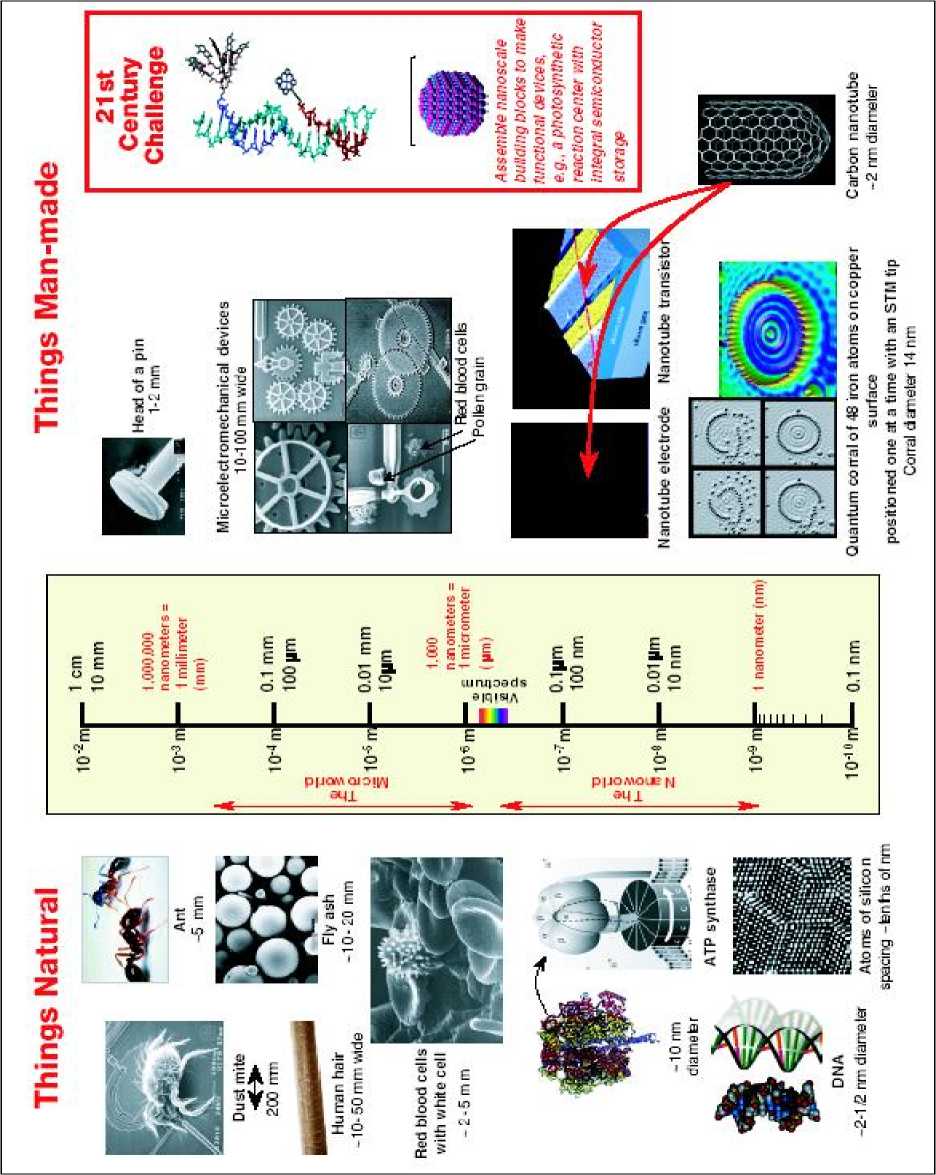
Figure 1. The size of nanoscale objects and phenomena compared with the size of small everyday objects (Courtesy of Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy)

In the last two decades, researchers began developing the ability to manipulate matter at the level of single atoms and small groups of atoms and to characterize the properties of materials and systems at that scale. This capability has led to the astonishing discovery that clusters of small numbers of atoms or molecules — nanoscale clusters — often have properties (such as strength, electrical resistivity and conductivity, and optical absorption) that are significantly different from the properties of the same matter at either the singlemolecule scale or the bulk scale. For example, carbon nanotubes are much less chemically reactive than carbon atoms and combine the characteristics of the two naturally occurring bulk forms of carbon, strength (diamond) and electrical conductivity (graphite).

Furthermore, carbon nanotubes conduct electricity in only one spatial dimension, that is, along one axis, rather than in three dimensions, as is the case for graphite. Nanoscale science and engineering also seek to discover, describe, and manipulate those unique properties of matter at the nanoscale in order to develop new capabilities with potential applications across all fields of science, engineering, technology, and medicine.

The National Nanotechnology Initiative (NNI) was established primarily because nanoscale science and technology are predicted to have an enormous potential economic impact. Many potential applications of nanoscale science and technology have been touted in both the scientific and the popular press, and there has been no shortage of promises made for the ability of nanoscale technology to revolutionize life as we know it. Beyond any speculation or hype, the committee can point to current applications of nanoscale materials and to devices that are already impacting our nation’s commerce, as well as advances that are mature enough to promise impacts in the near future.

Figure 2 is a time line for anticipated impacts.

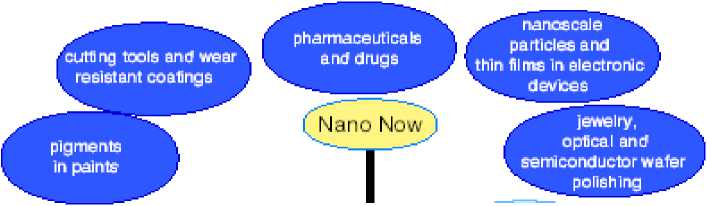
^^ nanoscaJa ^^ particles and thin films In electronic ^ devteea j

" jewelry, ™ optical and semiconductor wafer ^ nonehing ^

Figure 2. Current applications of nanotechnology and time line for anticipated advances

Some of the current impacts, as well as anticipated longer-term impacts, of the technical revolution that will be ushered in by nanoscale science and technology are discussed in more detail below.

In these report we are describe methods to control quantum systems in the arena of quantum and atomic optics and quantum nano-mechanics. We will explore the following question: What is feedback in Nature and rather than controlling, say, a jet engine, can we use feedback to control an object as small as a single atom?

Feedback in Nature

Many cutting edge problems in the natural sciences involve understanding aggregate behavior in complex large-scale systems. This behavior “emerges" from the interaction of a multitude of simpler systems, with intricate patterns of information flow. Representative examples can be found in fields ranging from embryology to seismology. Researchers who specialize in the study of specific complex systems often develop an intuitive emphasis on analyzing the role of feedback (or interconnection) in facilitating and stabilizing aggregate behavior, and it is often noted that one can only have hope of deep understanding if it is somehow possible for theories of collective phenomenology to be robust to inevitable uncertainties in the modeling of fine-scale dynamics and interconnection.

While sophisticated theories have been developed by domain experts for the analysis of various complex systems, the development of rigorous methodology that can discover and exploit common features and essential mathematical structure is just beginning to emerge. The range of applications for which tools in Control, Dynamics, and Systems (CDS) are relevant is expanding rapidly as advances in science and technology create new understanding of the underlying dynamics and the importance of feedback in a wide variety of natural and technological systems, and new sensors and actuators allow investigation and manipulation of phenomena at heretofore unimagined levels of detail.

• A.    The Magic of Feedback . Feedback has many interesting and useful properties. It makes it possible to design precise systems from imprecise components and to make physical variables in a system change in a prescribed fashion. An unstable system can be stabilized using negative feedback and the effects of external disturbances can be reduced. Feedback also offers new degrees of freedom to a designer by exploiting sensing, actuation and computation. A consequence of the nice properties of feedback is that it has had major impact on man-made systems. Drastic improvements have been achieved when feedback has been applied to an area where it has not been used before.

• B.    Drawbacks of Feedback . While feedback has many advantages, it also has some drawbacks. Chief among these is the possibility for instability if the system is not designed properly. We are all familiar with the effects of “positive feedback" when the amplification on a microphone is turned up too high in a room. This is an example of feedback instability, something that we obviously want to avoid. This is tricky because of the uncertainty that feedback was introduced to compensate for: not only must we design the system to be stable with the nominal system we are designing for, but it must remain stable under all possible perturbations of the dynamics. Another potential drawback of control is the complexity of embedding a control system into a product. While the cost of sensing, computation, and (to a lesser extent) actuation has decreased dramatically in the past few decades, the fact remains that control systems are often very complicated and hence one must carefully balance the costs and benefits. An early engineering example of this is the use of microprocessor-based feedback systems in automobiles. The use of microprocessors in automotive applications began in the early 1970s and was driven by increasingly strict emissions standards, which could only be met through electronic controls. Early systems were expensive and failed more often than desired, leading to frequent customer dissatisfaction. It was only through aggressive improvements in technology that the performance, reliability and cost of these systems allowed them to be used in a transparent fashion. Even today, the complexity of these systems is such that it is difficult for an individual car owner to fix problems, although the reliability has risen to the point that this is no longer a major issue.

• C.    Feedforward . When using feedback that there must be an error before corrective actions are taken. Feedback is thus reactive. In some circumstances it is possible to measure a disturbance before it enters the system and this information can be used to take corrective action before the disturbance has influenced the system. The effect of the disturbance is thus reduced by measuring it and generating a control signal that counteracts it.

This way of controlling a system is called feedforward. Feedforward is particularly useful to shape the response to command signals because command signals are always available. Since feedforward attempts to match two signals, it requires good process models otherwise the corrections may have the wrong size or it may be badly timed. The ideas of feedback and feedforward are very general and appear in many different fields. In economics feedback and feedforward are analogous to a market-based economy versus a planned economy. In business a pure feedforward strategy corresponds to running a company based on extensive strategic planning while a feedback strategy corresponds to a pure reactive approach. The experience in control indicates that it is often advantageous to combine feedback and feedforward. Feedforward is particularly useful when disturbances can be measured or predicted. A typical example is in chemical process control where disturbances in one process may be due to processes upstream. The correct balance of the approaches requires insight and understanding of their properties.

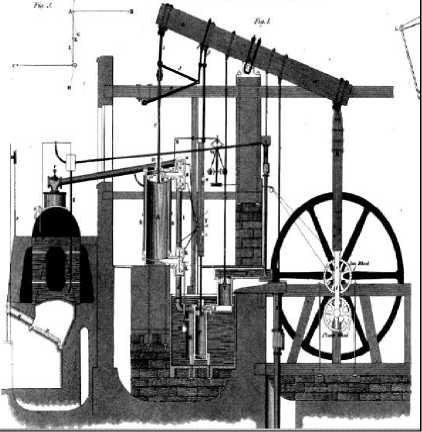
Watt’s Governor (WG), which was built in 1782, might be the very first machinery to solve automatically a control problem.

Figure 3 shows the structure and hardware of WG.

( a )

(b)

Figure 3. Structure (a) and hardware (b) of WG

As an automatic control tool, Watt’s governor aims to conserve some physical properties of a system subject to stochastic noise while maintaining its internal dynamics. Schematically, the WG can be viewed as a two steps process, measurement and correction. At the first step a measurement of the system is performed to check whether the constraint has been violated. Next, if such a violation was found, a correction step takes place, and drives the system back to the allowed boundaries.

A quantum Governor is a natural requirement when the limit of nano-machines is approached. Quantum computing is another candidate for such a device. However, quantum mechanics imposes non trivial restrictions on the development of the quantum Governor. A measurement, which is a main feature of the classical WG intervenes in the dynamics of quantum systems and it therefore should be avoided or reduced to a minimum. A control scheme is traditionally categorized either as an open-loop or a closed-loop control. In the closed-loop control scheme one tries to extract information from a feedback from the quantum system in a way that allows the control of the system (see, Figure 4).

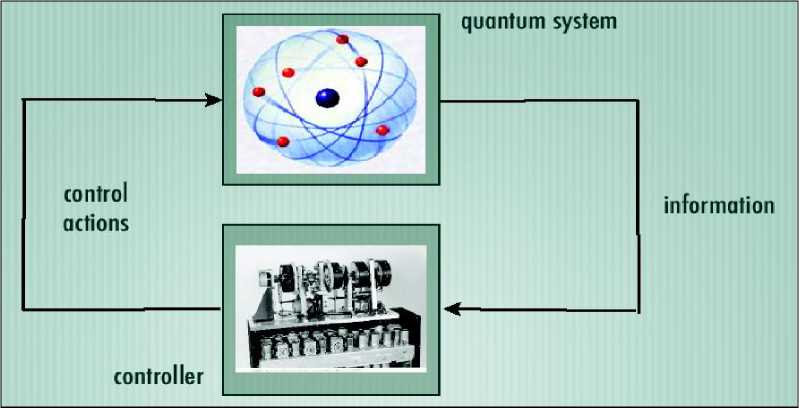
Figure 4. Structure of closed-loop quantum control system

Closed loop - control actions depend on information gained as the system is operating. Closed loop means feedback, just like in Watt’s steam engines.

Let us consider types of Quantum Feedback . The classical measurement results are used by the controller (e.g. classical electronics) to provide a classical control signal (see, Figure 5).

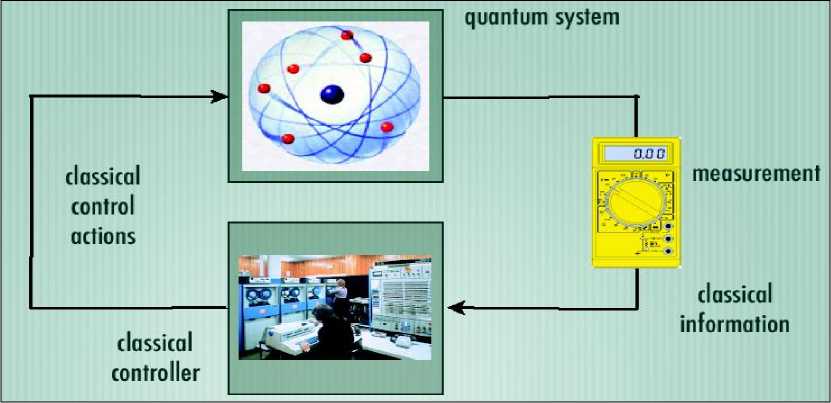
Figure 5. Controller with a classical control signal

In order to realize the QG a tool that distills quantum systems in some automatic fashion, has to be built. Distillation steps usually reduce the density of the system, and hence, in order to conserve the density of a controlled system, an extra-step to enrich the system and compensate for the losses is also required.

Quantum feedback control when we really need to design with quantum limits in mind.

Figure 6 shows the example of real laboratory quantum control system with measurement.

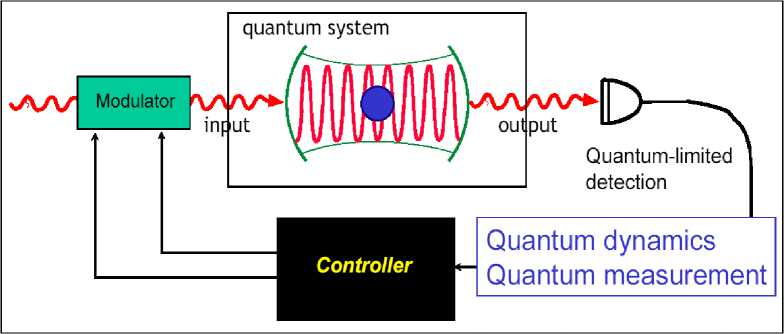
Figure 6. Quantum feedback control system

In this control system we can change measurement or even dynamics at any stage depending on photocurrent.

Outline of quantum measurements and closed loop control is as following: controlling the counting statistics of the optical field; adaptive phase measurements; continuous measurements/quantum trajectories; quantum trajectory approach to feedback.

For the case when not using measurement controller is also a quantum system, and feedback involves a direct flow of quantum information (see, Figure 7).

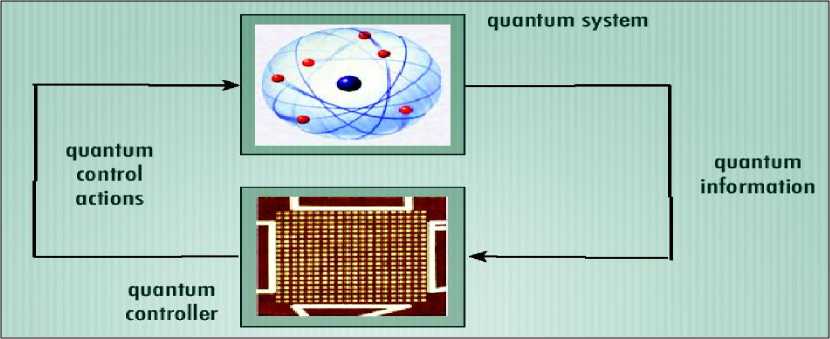
Figure 7. Controller without measurement

An open-loop control scheme corrects the system without any measurement. Open loop - control actions are predetermined, no feedback is involved.

Figure 8 shows an open-loop control scheme.

Figure 8. An open-loop control scheme

Regardless of the controller that is used, there are three major qualitative objectives that must be considered when assessing the quality of the feedback system.

• 1.    Performance is the ability of the controller to realize its dynamical objective, such as to achieve the target value, y * ( T ) , or to follow a reference signal, r(t).

• 2.    Stability is a measure of how well-behaved the control system is. When feedback is utilized, there is the potential for instability. If caution is not taken when designing the feedback system, parasitic signals or environmental disturbances might cause the entire dynamical system to oscillate out of control and potentially experience physical damage.

• 3.    Robustness is the ability of the controller to remain effective despite unanticipated changes in either the system being controlled or the environment.

In general, realistic controllers must achieve a balance ( trade-off principle) between performance, stability and robustness. We will explore the trade-offs between tracking, robustness and stability, and will develop a designing procedure. Also in general, controller design is an immense and involved subject, especially when robustness is required. The particular objective that is most important is application dependent. For example, in an airplane, robustness and stability take higher priority than performance. This is because it is preferable for a plane to go slightly of course than it is for it to become unstable and potentially crash. However, in precision measurement, the opposite is true, and it is better for a laser or an interferometer to achieve high performance at the expense of having to relock it every few days, or when someone drops a screwdriver on the optical table. We briefly highlight four application areas of feedback here.

Biological Systems

At a variety of levels of organization - from molecular to cellular, to organismal, to populational - biology is becoming more accessible to approaches that are commonly used in engineering: mathematical modeling, systems theory, computation, and abstract approaches to synthesis (synergetic approach). Conversely, the accelerating pace of discovery in biological science is suggesting new design principles that may have important practical applications in man-made systems. This synergy at the interface of biology and engineering offers unprecedented opportunities to meet challenges in both areas. The principles of control are central to many of the key questions in biological engineering and will play an enabling role in the future of this field. A major theme currently underway in the biology community is the science of reverse (and eventually forward) engineering of biological control networks (such as the one shown in Figure 9).

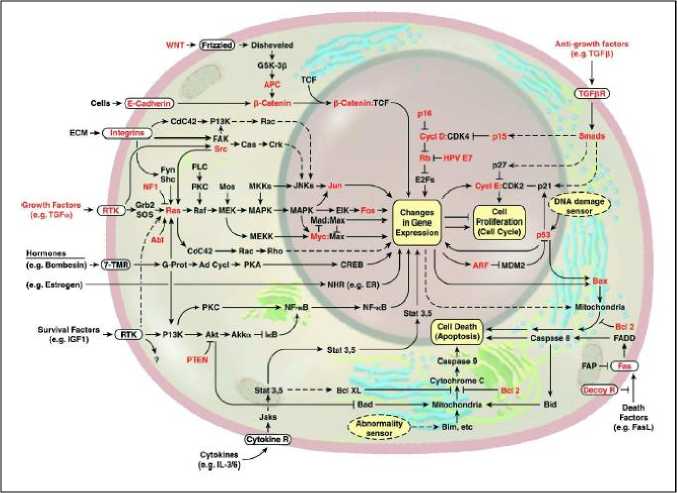
Figure 9. The wiring diagram of the growth signaling circuitry of the mammalian cell

There are a wide variety of biological phenomena that provide a rich source of examples for control, including gene regulation and signal transduction; hormonal, immunological, and cardiovascular feedback mechanisms; muscular control and locomotion; active sensing, vision, and proprioception; attention and consciousness; and population dynamics and epidemics. Each of these (and many more) provides opportunities to figure out what works, how it works, and what we can do to affect it.

Ecosystems

In contrast to individual cells and organisms, emergent properties of aggregations and ecosystems inherently reflect selection mechanisms which act on multiple levels, and primarily on scales well below that of the system as a whole. Because ecosystems are complex, multi-scale dynamical systems, they provide a broad range of new challenges for modeling and analysis of feedback systems. Recent experience in applying CDS tools to bacterial networks suggests that much of the complexity of these networks is due to the presence of multiple layers of feedback loops that provide robust functionality to the individual cell. Yet in other instances, events at the cell level benefit the colony at the expense of the individual. Systems level analysis can be applied to ecosystems with the goal of understanding the robustness of such systems and the extent to which decisions and events affecting individual species contribute to the robustness and/or fragility of the ecosystem as a whole.

Quantum Systems

While organisms and ecosystems have little to do with quantum mechanics in any traditional scientific sense, complexity and robustness issues very similar to those described above can be identified in the modern study of quantum systems. In large part, this sympathy arises from a trend towards wanting to control quantum dynamics and to harness it for the creation of new technological devices. At the same time, physicists are progressing from the study of elementary quantum systems to the study of large aggregates of quantum components, and it has been recognized that dynamical complexity in quantum systems increases exponentially faster with system size than it does in systems describable by classical (macroscopic) physics. Factors such as these are prompting the physics community to search broadly for new tools for understanding robust interconnection and emergent phenomena (based on quantum computing tools). Modern scientific research is rapidly evolving a field of quantum engineering. Driven by technology goals in areas such as quantum information processing, nano-electromechanical sensing, chemical synthesis, trace gas detection, and ultrahigh-bandwidth optical communication, researchers are beginning to formulate strategies for achieving robust performance with physical devices or systems in which quantum mechanical effects are prominent. Mathematical tools from CDS for analysis and synthesis could have a profound impact on activities of this kind.

A schematic diagram of a modern quantum control experiment is show in Figure 10a.

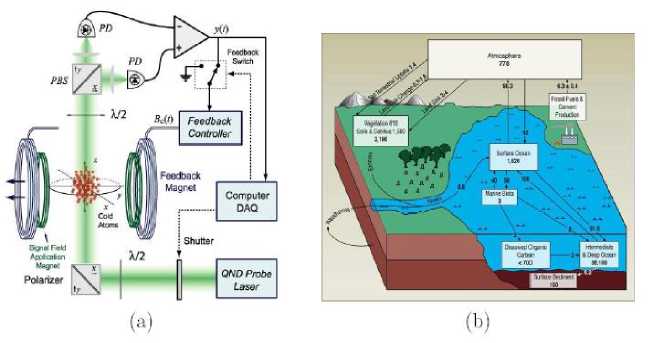
Figure 10. Examples of feedback systems in nature (a) quantum control system and (b) global carbon cycle

Environmental Science

It is now indisputable that human activities have altered the environment on a global scale. Problems of enormous complexity challenge researchers in this area. And first among these is to understand the feedback systems that operate on the global scale. One of the challenges in developing such an understanding is the multi-scale nature of the problem, with detailed understanding of the dynamics of micro-scale phenomena such as microbiological organisms being a necessary component of understanding global phenomena, such as the carbon cycle illustrated Figure 10b. The reader can find more detail descriptions and attention to the role of feedback in control system theory in the following book: K.J. Astrom and R.M. Murray, “Feedback systems: An introduction for scientific and engineering,” DRAFT Vol.915, 2004, (see web site: ; and review article: J. Bechhoefer, “Feedback for physicists: A tutorial essay on control,” // Reviews of Modern Physics, Vol. 77, No 4, 2005, pp. 783 – 836.

Quantum optimal feedback control

Unlike classical systems, quantum systems may be easily disturbed when information about the system is extracted. Measurement disturbs a quantum system through the following intrinsic property of quantum mechanics: obtaining accurate knowledge about one observable of a quantum system necessarily limits information about an observable conjugate to the first. For example, particle position and particle momentum are conjugate observables, and the uncertainties inherent in the knowledge of both are codified by the famous Heisenberg uncertainty relation. If the chosen feedback control strategy involves measurement, one must take into account the 'back-action' of the measurement on the evolution of the quantum system. A generally applicable model for including back-action is the model of continuous quantum measurement. This model was developed for quantum optics where such measurements have been realized experimentally, and it was also derived in the mathematical physics literature using more abstract reasoning.

One area in which it should be possible to test quantum feedback control in the near future is atomic optics. It has already been demonstrated that a single atom can be trapped inside an ultra-low-loss optical cavity (in the strong coupling quantum regime). By strong coupling one refers to the radiative atom-cavity coupling which is proportional to the induced atomic dipole moment and the single-photon cavity field. Continuous measurements and real-time feedback could be used to cool such an atom to the 'ground' state of the quantized mechanical potential produced by several photons in the cavity. The average number of photons circulating inside such a cavity can be maintained at a very low value N ~ 1-10 by using a very weak driving laser that barely balances the slow rate at which individual photons leak out. If the cavity mode volume is sufficiently small, just a few photons can give rise to dipole (AC Stark-shift) forces that are strong enough to bind an atom near a local maximum of the optical field distribution. At the same time, the atomic motion can be monitored in real time via phase-sensitive measurements of the light leaking out of the cavity. To a degree determined by the fidelity of these measurements, the information gained can be used continually to adjust the strength of the driving laser (and hence the depth of the optical potential) in a manner that tends to remove kinetic energy from the atomic center-of-mass motion.

In order to perform such a task in real time, however, it is essential to develop approximate techniques for continuously estimating the state of the atomic motion. This is because the full solution for the continuous estimate is given by integrating a stochastic master equation , and this integration is far too complex to be performed in real time. While this experiment remains to be carried out, an approximate estimation algorithm has been developed, and its use in combination with an experimentally realizable feedback algorithm verified numerically.

Figure 11 shows an example of cooling an atom trapped in an optical cavity with active feedback based on changing the driving laser amplitude as a function of the homodyne measurement record. The blue curve shows the cooling when a Gaussian estimator for the atomic state is used, the orange curve when the cooling is based only on the output photocurrent from the detector, and the dashed green curve shows what happens when there is no cooling but only observation: as described above, the system is 'heated' by the measurement process.

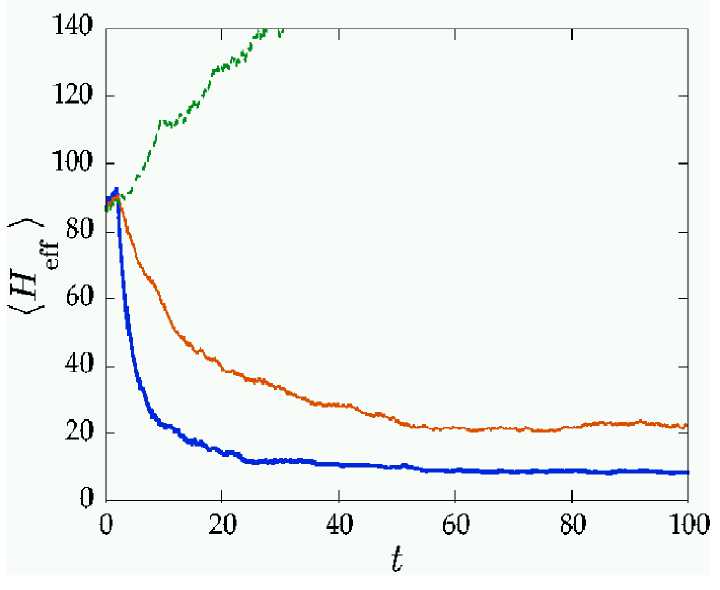
Figure 11. An example of cooling an atom trapped in an optical cavity with active feedback

Yet another situation where such active cooling is possible arises in quantum nano-mechanics. Here, the position of a nano-resonator can be detected via a single-electron-transistor (SET); sensing of the SET current can be used to measure the nano-resonator position. Feedback can then be applied by another electrode capacitive coupled to the nano-resonator beam. We have analyzed the performance of such an active cooling system and find that it can be used to cool nano-resonators very close to their ground states.

Figure 12 shows the final temperature achievable as a function of gate voltage (measurement strength) for various values of the oscillator Q (better performance for higher Q).

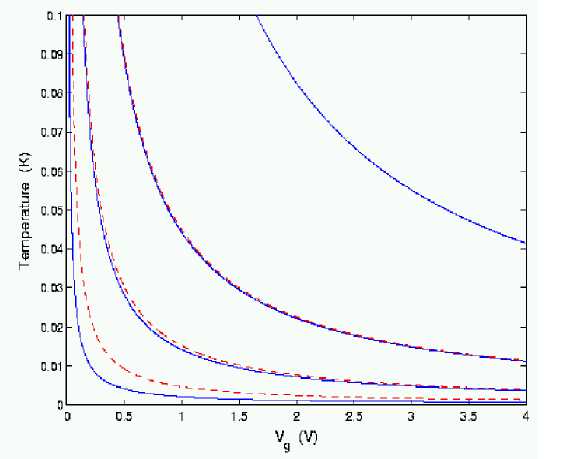
Figure 12. The final temperature achievable as a function of gate voltage for various values of the oscillator Q. [The dashed red curves in Figure 12 are a more conservative estimate of the cooling taking into account uncertainties in the theoretical modeling of the SET].

Over the past decade, a variety of optimal control calculations have been performed for the purposes of exploring the manipulation of quantum phenomena. Recently, a number of successful closed-loop optimal control experiments have also been carried out where the optimal fields were directly identified in the laboratory using suitable learning control techniques. Seeking optimality is natural, as achieving the best possible quantum system performance is always desirable. Of special interest is the contribution of dynamical coherences, as manifested through the manipulation of constructive and destructive quantum wave interferences. There is only an incomplete understanding of the role of such interferences, especially in the most interesting cases involving strong field control, where quantum systems exhibit highly nonlinear field effects. An early point of speculation was that even modest field noise would effectively “kill” the successful achievement of quantum control in the strong-field regime, where the quantum system would act to amplify the field noise. The intriguing recent experiments operating in this regime give very encouraging evidence that this speculation was incorrect. However, the detailed mechanism for the surprising degree of robustness has remained unclear, especially with successful optimal control being observed in diverse systems, suggesting that this behavior may be generic.

As experimental technology continues to improve, the idea of actively manipulating micro-scale quantum processes — rather than just merely observing them — is rapidly gaining ground and, indeed, already being demonstrated. As a result of these advances, it is expected that sooner or later quantum technologies of quite some complexity will exist. It is important to note that all classical complex engineered systems make essential use of feedback control in their operation.

The question arises whether some form of quantum feedback control is available to be applied to future quantum technologies and, if so, how different is it from its classical counterpart?

A quantum feedback control block diagram, in general form, is looked very similar to its classical counterpart (see, Figure 13).

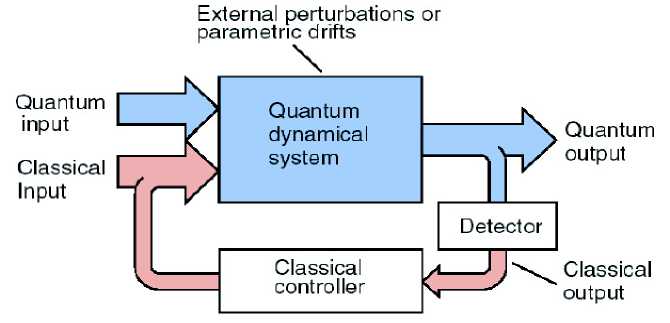
Figure 13. Schematic of a quantum feedback control system

The output from a detector is sensed in order to control the parameters of the Hamiltonian and thereby affect changes in the output, if needed. While the basic principles are the same, there are several key differences. Classically, the more one can know about the system, the better of one is with regard to predicting the system behavior and hence in being able to control it. Quantum mechanically, however, due to the existence of measurement backaction one has to be careful in designing how the measurements are carried out, as the very act of measurement can render the future behavior of some quantity to be controlled, more, not less, uncertain. In addition, approaching the quantum limit is difficult in terms of keeping the system sufficiently isolated from external disturbances and the implementation and design of ideal quantum detectors remains an open issue. Finally, the actual control implementation requires significantly more computation than compared to classical feedback.

The work in quantum feedback control has covered not only important theoretical aspects, but also realistic implementation scenarios in cavity quantum electrodynamics QED and nano-mechanics experiments. In both of the latter, we have focused on the question of whether a quantum system can be cooled to its ground state, or very near to it, using quantum feedback methods.

Example 1. In the cavity QED experiments, an atom is trapped in an optical micro-cavity in the strong-coupling regime, and the output laser light is monitored via homodyne detection. The resulting photocurrent provides information about the position of the atom in the cavity, which, in turn can be used to cool the atom by varying the intensity of the driving laser field. One of the key results in this work is the demonstration that a simplified Gaussian estimator provides very good cooling performance (see, Figure 14, [Top: cooling based on the Gaussian estimator. Bottom: cooling based on perfect knowledge of the actual wave function]).

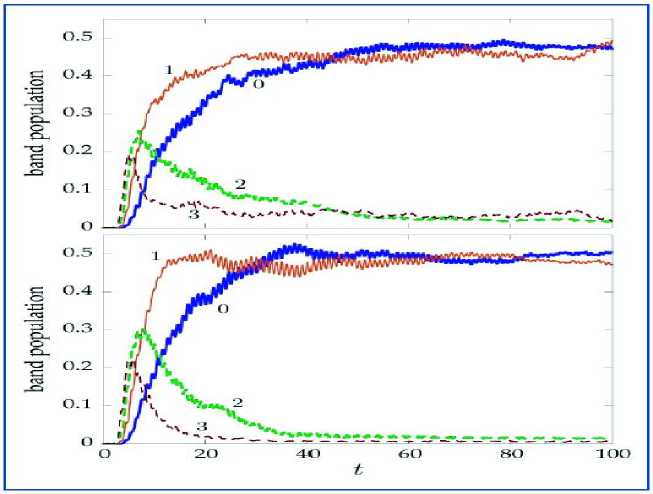
Figure 14: Evolution of the band populations for the lowest four energy bands of the optical lattice, averaged over 128 trajectories

Because the feedback can only be applied in a symmetric way, the state cools to an equal mixture of the ground and first excited state. But, at this point, spectroscopic techniques can be used to cool to the ground state. Detailed calculations to fully understand the behavior of this system are ongoing on parallel supercomputers at Los Alamos National Laboratory (LANL).

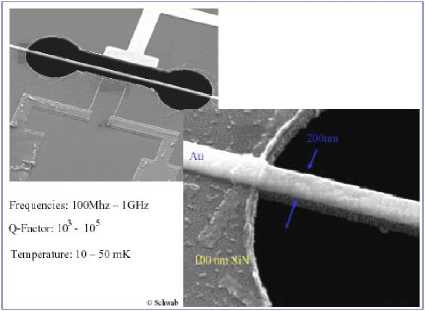
Example 2 . Nano-resonator technology has reached the point that resonators are now being built that are less than a factor of 10 away from the quantum limit. The quantum limit is reached when the thermal energy is less than the ground state energy of the resonator. To achieve this, one could either lower the resonator temperature to mK , or increase its frequency, which in turn increases the ground state energy. It turns out that lower frequency resonators are much easier to deal with experimentally (lower losses, better measurement coupling), thus, if possible, it would be preferable to cool the resonator below temperatures achievable with a dilution refrigerator. The study of a feedback cooling scheme based around a single electron transistor used as a position sensor for the resonator, with a feedback signal applied via a control electrode is shown on Figure 15.

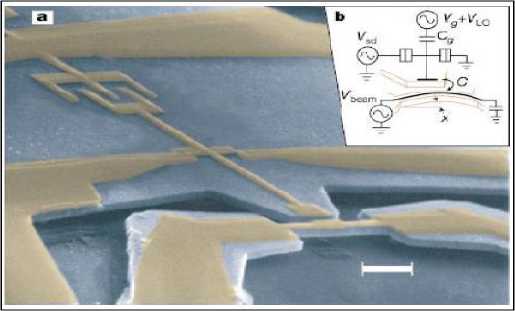
(a)

(b)

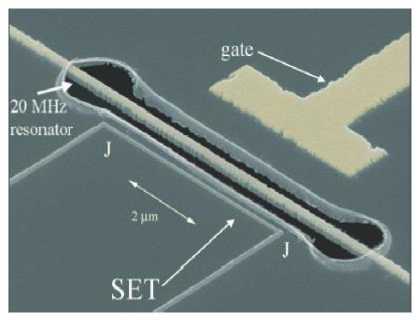
Figure 15: A nano-mechanical resonator (courtesy Keith Schwab, LPS) mechanical part; (b) electric scheme; (c) general structure view

(c)

The thin central bar is coated with gold in order to bias it, as is the T -shaped electrode to the left. The thin line parallel to the resonator is the gate of a single-electron transistor, which serves as the quantum sensor. Feedback is applied by varying the potential on the left electrode.

Remark . These devices have been built in Keith Schwab’s laboratory at the Laboratory for Physical Sciences (LPS), Maryland. Successful feedback cooling has been demonstrated but has not yet led to a quantum-limited resonator.

Several theoretical and experimental studies provide the relevant background for the analysis in this report. An optimally designed field for the dissociation of hydrogen fluoride showed excellent robustness to field fluctuations, and learning control simulations indicate that closed-loop experiments should naturally gravitate towards control fields that produce robustness with respect to the presence of field fluctuations. Simulations suggest that explicitly seeking robustness (as an additional control criteria) can further enhance this stable behavior, and in favorable cases, even with little deterioration in the quality of the attained objective.

Most significant are the recent laboratory demonstrations of high harmonic generation. Lurking behind all of these observations is the unknown degree of ‘‘quantum character’’ retained in the control process, especially in the presence of field fluctuations. In some special instances, field fluctuations may be helpful, but the general expectation is that field noise will be deleterious at least to some extent. The presence of field noise may also influence the rate of convergence or other algorithmic aspects of the laboratory learning control process.

Quantum mechanics, though a probabilistic theory, gives a “deterministic” answer to the question of how the present determines the future. In essence, in order to predict future probabilities, we need to (numerically) propagate the time dependent Schrödinger equation from the present to the future.

The field of Quantum Control deals with an important modification of this task, namely, it asks: Given a wave function in the present, what dynamics (e.g. the Hamiltonian) guarantees a desired outcome (“objective”) in the future?

We will explore the relationship between (a) the nature of coherent quantum dynamics, (b) the influence of field fluctuations, (c) the degree of robustness, and (d) the attainment of optimality. It will be shown that the bilinear dependence of quantum expectation values upon the evolution operator and it’s adjoin has a special serendipitous role in relating all of these points. Detailed simulations of the phenomena involved are difficult to perform, especially for the most interesting complex chemical/physical systems. However, under certain simple assumptions and dynamical considerations, it will be shown that a clear physical picture emerges. The physical picture and its consequences are consistent with current observations and should ultimately aid in providing mechanistic insights into the control of quantum phenomena. Under the most severe degrees of control field fluctuations, the quality of the achieved objective should eventually diminish

Электронный журнал «Системный анализ в науке и образовании» Выпуск №1, 2018 год significantly. However, before that occurs, it will be argued that even the loss of multiple pathway interferences may still lead to successful quantum control processes.

In practice one can modify the Hamiltonian by introducing external fields (e.g. laser light). It is then possible to reach the objective in a “trial-and-error” fashion, that is, one can guess a Hamiltonian, propagate the initial wave function to the future, compare the result with the desirable objective, and correct the guess for the Hamiltonian until satisfactory agreement with the objective is reached. A systematic way of executing this procedure is the sub-field called optimal control.

This trial-and-error method is very time consuming, requiring the repeated solution of the time dependent Schrödinger equation. When the explicit time-dependent terms in the Hamiltonian merely serve to prepare a state which then evolves in the absence of an external field, or when its explicit time dependence can be treated adiabatically, there exists a much more elegant method, called coherent control (CC), which necessitates the solution of the (time-independent) Schrödinger equation only once. Moreover, in that case, the CC solution allows for the simultaneous exploration of other possible future outcomes (and not just a single “desirable” objective) resulting from different preparations of the initial wave function. The CC method is also the subject of the present report.

In this expository report is demonstrated, in particular, estimation and feedback control of quantum mechanical systems in what is essentially a non-commutative version of the binomial model that is popular in mathematical finance. The model is extremely rich and allows a full development of the theory, while remaining completely within the setting of finite-dimensional Hilbert spaces (thus avoiding the technical complications of the continuous theory). We introduce discredited models of an atom in interaction with the electromagnetic field, consider filtering equations for photon counting and homodyne detection, and describe a stochastic control problem using dynamic programming and Lyapunov function methods.

Though it is not directly visible in our everyday lives, the technology to manipulate matter at the level of single atoms and photons is well in place and is progressing at a fast rate. Nobel Prize winning technologies such as laser cooling and trapping of atoms, which were state-of-the-art only a decade ago, are now routine procedures which are being applied in physics laboratories around the world. The generation of highly coherent light and the detection of single photons have been refined since the development of the laser. Given the availability of this unprecedented level of control over the microscopic world, the question of control design seems a timely one - one could wonder whether we can “close the loop” and make the atoms do useful work for us. This is the domain of quantum feedback control.

Remark. “Quantum,” of course, refers to the theory of quantum mechanics, which comes in necessarily at this level of description. Controlling an atom using feedback means that we need to be performing measurements on the atom, and measurements in quantum mechanics are inherently random. This makes the theory both challenging and interesting from the point of view of fundamental physics and control theory.

As we will demonstrate, the theory of quantum feedback control resembles closely, and follows directly in many parts, the (classical) theory of stochastic control. Several promising applications of quantum feedback control have been proposed and are now starting to be investigated in a laboratory setting. One class of such applications falls under the general heading of precision metrology: can we utilize the sensitivity of small numbers of atoms to external perturbations to design ultrafast, precise sensors, when the desired accuracy is on the order of the intrinsic quantum uncertainty of the sensor?

Remark. Quantum EMS are, for example, nano-to-micrometer (micron) scale mechanical resonators coupled to electronic devices of comparable dimensions, such that the mechanical resonator behaves in a manifestly quantum manner. We review progress towards realizing quantum EMS, beginning with the phononic quantum of thermal conductance for suspended dielectric wires. We then describe efforts to reach the quantum zero-point displacement uncertainty detection limit for (sub) micron-scale mechanical resonators using the single electron transistor as displacement transducer. A scheme employing the Cooper-pair box as coherent control device to generate and detect quantum superposition of distinct position states is then described. Finally, we outline several possible schemes to demonstrate various other quantum effects in (sub)micron mechanical resonators, including single phonon detection, quantum squeezed states and quantum tunneling of mechanical degrees of freedom.

Thus quantum EMS, or QEMS for short, is an emerging branch of mesoscopic physics made possible by recent advances in micro-fabrication technology. A QEMS device typically comprises a nano-to-micron scale mechanical resonator, such as a cantilever (suspended beam which is clamped at one end) or bridge (suspended beam clamped at both ends), which is electro-statically coupled to an electronic device of comparable dimensions, such as a single electron transistor (SET). While a mechanical resonator comprises three times as many normal vibrational modes as it does atoms, only the lowest, few flexural modes will strongly couple to the electronic device. Provided that the quality factors of these lowest modes are very large, then for small amplitudes the mechanical resonator behaves electively like a few independent damped harmonic oscillators. The quality factor for a given oscillator is defined as following: Q = ωτ , where ω is the oscillator angular frequency and τ is the energy decay time-constant, i.e., the time taken for the energy stored in the oscillator to decay by a factor from its initial value. Measured quality factors of the lowest modes of nano-to-micron scale mechanical resonators in moderate vacuum are typically in the range 10³ - 10⁴. With the appropriate temperature and vacuum conditions, and device operating parameters, these oscillators will behave in a manifestly quantum manner, as indirectly evidenced through the electronic device behavior.

Concrete applications include e.g. precision magnetometry, which was recently investigated in a laboratory experiment (see, below Figure 16), and atomic clocks. The metal boxes in the foreground are diode lasers, whose output light is manipulated using a large number of optical elements. In the background on the left is a magnetically shielded chamber containing magnetic coils and a cell with laser cooled Cesium atoms. A schematic of the experiment is shown on the right. (Photograph courtesy of John Stockton.) A second class of examples involves the design of optical communication systems where each bit is encoded in a pulse containing only a small number of photons; see below for a related experimental demonstration.

As a third application, we mention the use of feedback for cooling of atoms or nano-mechanical devices, see below for a laboratory demonstration (the availability of efficient cooling techniques is important in experimental physics). As both the theory and applications are still in their infancy, it is far from clear at this time what the ultimate impact of quantum feedback control will be; it is clearly unlikely that future generations of washing machines or airplanes will be powered by quantum control, but other application areas, such as the ones mentioned above, might well benefit from the availability of such technology. At the very least, however, the questions that arise in the subject prompt us to explore the fundamental limits on the control and engineering of physical systems, and a fruitful interplay between control theory and experimental physics enables the exploration of these limits using real-life experiments such as the one displayed in Figures 10 and 16.

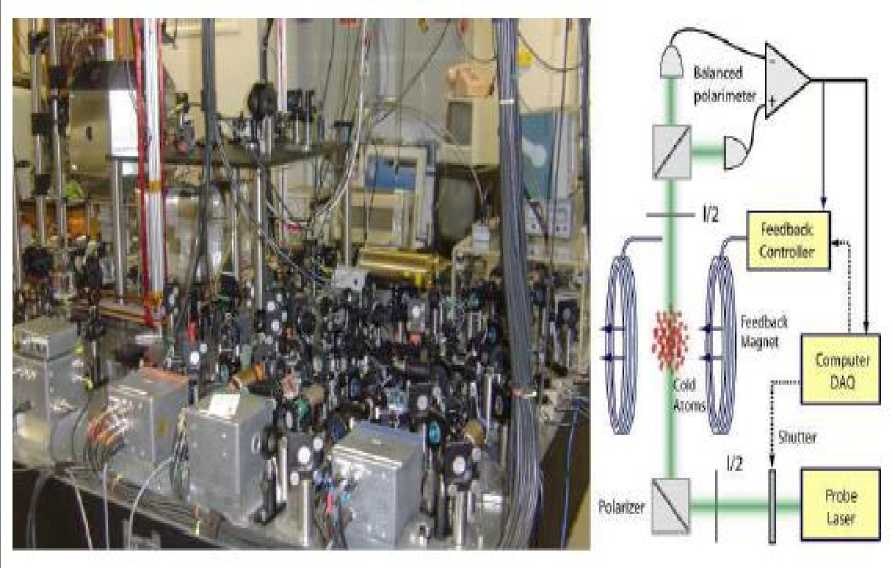
Figure 16. A laboratory experiment in quantum feedback control, implementing the setup reported

In this report is demonstrated the underlying theory using a simple but rich toy models; we hope that the reader is sufficiently intrigued to come along for the ride.

Remark : Related works . The study of quantum feedback control was pioneered by V.P. Belavkin in a 1983 paper, long before the experimental realization of such a setup was realistically feasible. Belavkin (see photo below) is realized that due to the unavoidable presence of uncertainty in quantum measurements, the theory of filtering — the extraction of information from noisy observations — plays a fundamental role in quantum feedback control, exactly as in the theory of stochastic control with partial observations. Feedback control was explored in discrete time using the operational formalism of Davies, which is the precursor of quantum filtering theory.

Belavkin developed further the theory of quantum filtering in a series of articles, and the use of dynamic programming for feedback control in continuous time was sketched. We refer to next special issue of these reports a modern introduction to quantum filtering theory. Independently from Belavkin’s work, the equations of quantum nonlinear filtering are developed in the physics literature by Carmichael, based on the work of Davies, under the name of “quantum trajectory theory”. Though the connection to filtering theory was not realized until much later, Carmichael’s work nonetheless spawned an investigation on the use of feedback control in the physics literature. It is here that most of the practical applications, such as the ones cited above, were proposed and developed.

Over the past decade it has become increasingly clear that feedback control of quantum systems is essentially a problem of stochastic control theory with partial observations. In this context, the system and observations are generally modeled as a pair of Ito (quantum) stochastic differential equations. It is then the goal of the control engineer to find a feedback control policy, depending on the system state only through the past history of the observations that achieves a particular control objective.

Both in classical and quantum stochastic control theory a major role is played by the filtering equation, which recursively updates the information state of the system under observation. Unfortunately, the theory is plagued by infinite-dimensionality of the information state which severely limits its practical applicability, except in a few select cases (e.g. the linear Gaussian case.) One solution proposed in classical filtering theory is that of the projection filter. In this scheme, the filter is constrained to evolve in a finite-dimensional family of densities through orthogonal projection on the tangent space with respect to the Fisher metric. We can apply and discuss this approach to the simple but highly nonlinear quantum model of optical phase bistability of a strongly coupled two-level atom in an optical cavity. We can observe near-optimal performance of the quantum projection filter, demonstrating the utility of such an approach.

In the case of linear system dynamics and observations and Gaussian initial conditions, the so-called optimal control problem can be solved exactly both classically and quantum-mechanically provided that a quadratic performance criterion is chosen. This means that the control objective is specified as an optimization problem, where a certain cost function (the performance criterion) of the system evolution and the control signal is to be minimized. The resulting Linear-Quadratic-Gaussian (LQG) control is widely used in many technological applications. An important feature of LQG theory is its separation structure: the optimal controller splits up into a part that updates the optimal estimate of the system state given the observations (the Kalman filter), and an optimal feedback law which is only a function of the state estimate.

Remark . It was originally suggested by Mortensen that the separation structure of LQG control carries over even to the nonlinear case. The problem now separates into the nonlinear filtering problem of finding the optimal estimate of the system statistics given the observations and the optimal control problem of finding a feedback law, based only on the filtered estimate that minimizes some performance criterion. The estimate propagated by the filter is often referred to as the information state as it contains all information of the system possessed by the observer. Unfortunately, nonlinear stochastic control is plagued by two rather severe problems. First, the information state is generally infinite-dimensional even for very simple nonlinear systems. Second, even in the finite-dimensional case the nonlinear optimal control problem is generally intractable. The latter can sometimes be alleviated by posing a less stringent control objective. Nonetheless nonlinear stochastic control remains an extremely challenging topic, both in the classical and quantum mechanical case.

Remark . The problems of controlling the processes of microcosm, including control of motion of atoms and molecules, have a rich history. Numerous works are devoted to the issues of control on the basis of quantum-mechanical models, but until recently the possibilities of control were considered in purely theoretical terms. The main difficulties of controlling the processes at the atom-molecule level lie in the small dimensions of the controlled objects and high velocity of the processes going on in them. The molecules of chemical substances (monomers) have size of the order of nanometers (1 nm = 10 ^{- 9} m), and the characteristic times of natural oscillations of the atoms in a molecule have the order of femtoseconds (1 fsec = 10 ^{- 15} s). Design of instrumentation for measurement and control within this space-time scale is a challenge to science and technology. Until recently, there existed no technical facilities for control of such fast processes. The situation changed at the late 1980's with the advent of superhigh-speed femtosecond lasers generating pulses of the order of tens or now even units of femtoseconds as well as the methods of computerized control of the form of laser pulses. A new line of chemical research, the so-called femtochemistry, arose. A. Zewail was awarded the 1999 Nobel Prize for the progress in this area. The advances in other methods of using the femtosecond lasers gave rise to the term “femtosecond technologies” or “femptotechnologies.” These technologies are used, in particular, to solve the problems of selective dissociation where one needs to break certain molecular bonds without affecting, wherever possible, the rest of them.

Several approaches to the control of molecular systems were suggested. M. Shapiro and P. Brumer used control on the basis of interference of two laser beams of different frequencies, amplitudes, and phases (the pumping-damping scheme). D.J. Tannor and S.A. Rice suggested two-pulse schemes of pumping-damping in the time domain. Methods of optimal control that are based, in particular, on the V.F. Krotov’s method were later used in pulse optimization. H. Rabitz and his collaborators considered various versions of optimal control under the classical and quantum descriptions of the dynamics of molecular motion. They put forward the idea of realizing the adaptive laser control of chemical reactions by means of the methods of search optimization (genetic algorithms) whose feasibility was corroborated experimentally (see below example).

One of the simplest problems from this class is the typical problem of dissociation of the diatomic molecule which is a convenient benchmark for comparing the advantages and disadvantages of different methods. M.E. Goggin and P.W. Milonni carried out a numerical feasibility study of dissociation of the hydrogen fluoride (HF) molecule under the action of periodically varying field (monochromatic laser radiation). They used a similar method to study dissociation by the two-frequency (bichromatic) action and demonstrated that the intensity of the dissociating field can be substantially reduced. W.K. Liu, B. Wu, and J.M. Yuan used chirping, that is, uniform variation of the frequency of external action, to estimate the intensity of a dissociating field. It was shown that the field intensity required for dissociation can be reduced even more.

Conclusions

Non-periodic feedback action offers new possibilities for control of the molecular systems. The main problems here lie in measuring the system state and realizing the control actions over the time intervals comparable with the period of molecule natural oscillations. Various feedback algorithms, including those of optimal control, can be found below and other works in References. Their common trait lies in that they are used to design the control action as a time function from the given model of the molecular system. In the computer experiments, one may assume that all the necessary signals are measured and the design algorithm is realized by the computer. As the result, the control signal will be generated as a time function, and its realization on the object is done already without measurements and feedback. Numerous uncertainties - the initial system state is not known precisely and the constructed control function is calculated inaccurately and realized with error - hinder the practical application of this method. Finally, the model of the molecule itself is imprecise because its parameters are not known precisely, and the choice itself between the classical and quantum descriptions is the matter of repeated discussions.