Models of quantum intelligent control pt.2: quantum optimal control

We will review puts into perspective the present state and prospects for controlling quantum phenomena in atoms and molecules. The topics considered include the nature of physical and chemical control objectives, the development of possible quantum control rules of thumb, the theoretical design of controls and their laboratory realization, quantum learning and feedback control in the laboratory, bulk media influences, and the ability to utilize coherent quantum manipulation as a means for extracting microscopic information. The preview of the field presented here suggests that important advances in the control of molecules and the capability of learning about molecular interactions may be reached through the application of emerging theoretical concepts and laboratory technologies [1-19].

• A.    Controlling Quantum Phenomena Recent years have witnessed rapid acceleration of research activity in the general area of controlling quantum phenomena. Most applications have considered laser control over electronic, atomic, and molecular motion, and the roots of the topic may be traced back to the earliest days of laser development in the 1960s. From its inception to the present time, the field of coherent control has been stimulated by the objective of selectively breaking and making chemical bonds in polyatomic molecules. U1-trafast radiative excitation of chemical bonds is often a spatially limited, local process on a molecular scale, and desirable reactive processes may occur before the spoiling redistribution of the excitation into other

molecular modes takes place. Under special circumstances, local excitation may be achieved by simply exploiting favorable kinematic atomic mass differences, but this is not a broadly applicable approach. The promise of CC, and especially its optimal formulation, is to create just the right quantum interferences to guide the molecule to the desired product.

After many years of frustrating theoretical and laboratory efforts, a recent burst of activity promises advances in controlling quantum phenomena. The present rejuvenation of the field is due to a confluence of factors. These include the establishment of a firm conceptual foundation for the field, the introduction of rigorous control theory tools, the availability of femtosecond laser pulse-shaping capabilities, and the application of algorithms for closed-loop learning control directly in the laboratory. The serendipitous marriage of concepts and techniques stimulated this report, which takes a distinct perspective as a preview, rather than a review, of the field of the CC of quantum phenomena.

The resurgence of activity aimed at controlling quantum systems is motivated by the unusual products or phenomena that may become accessible. The long-standing goal of creating novel stable or metastable molecules still is an important objective. For example, ozone has been predicted to exist in a ring configuration of high energy content, but conventional photochemistry preparation techniques have failed to create this molecule in the gas phase. Another example is the isomerization of acetylene to form vinylidene, a reagent of considerable chemical interest. The hope in such cases is that the manipulation of molecular motion-induced quantum interferences will open up products or molecular states that are not easily attainable by conventional chemical or photochemical means. Laser-driven coherently controlled molecular dynamics is envisioned to have special capabilities for coaxing the atoms into forming the desired products. Although successful demonstrations of coherent laser control have at long last been performed, the challenge ahead is to fully demonstrate the superior capabilities of coherent molecular manipulation.

One significant recent change in the field is the rapid growth in the type of applications of controlled quantum phenomena being considered, including their use for control of electron transport in semiconductors and the creation of quantum computers. Although these directions are distinct from the original goal of controlling chemical reactions, a most important point is that the operating principle for quantum control of any type is the manipulation of constructive and destructive quantum mechanical interferences.

Application of this principle can be viewed as a micro-world extension of the traditional double-slit wave interference experiment, and the concept has been demonstrated many times in recent years, with an illustration of two-photon absorption in ^Na shown in Figure 1, a and b.

In this case, the analog of interference produced by the slits is now created by interfering the different pathways ( ^ + to ₂) and ( ^ '+ to ’ ) between the initial ( 3 s ) and final ( 5 s ) atomic states.

Remark . The upper level is excited by pairs of photons when the sum of their energies (for example, ( to + to ₂) and ( to '+ to ’ ) ) equals the two-photon resonance. Because a femtosecond pulse of width A to is spectrally broad, many distinct pairs exist, representing different paths. If the phase between the different paths is appropriately chosen, then constructive or destructive interference occurs leading to maximization or minimization of the two photon transition probability. (The femtosecond laser can be tailored to modulate the phases using a pulse shaper controlled by a learning algorithm, as shown in Figure 2). The 330-nm fluorescence of Na(4p) ^ Na(3s) is used as the feedback signal to the algorithm. The upper panels show typical learning control convergence curves for the two different cases when evolutionary algorithms are applied. The lower panels show the envelopes of the electric fields of the two optimized phase-shaped pulses.

The paths may combine either constructively to maximize the absorption signal (Figure 1 B, left) or destructively to minimize the signal (Figure 1 B, right). In more general applications in molecules, achieving high-quality control that cleanly discriminates among the accessible final product states naturally demands playing on multiple molecular "slits" (that is, many interfering pathways) by introducing flexible laser controls that can fully cooperate with the dynamic capabilities of the molecule. This calls for a short laser pulse where the phase and amplitude of the frequency components are controllable. As the principles and techniques are often quite similar in the different applications of controlled quantum phenomena, this preview focuses on molecular applications.

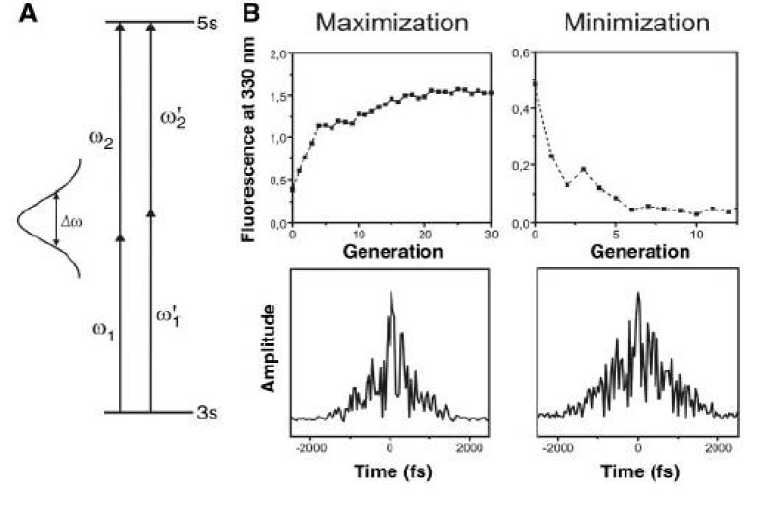
Figure 1. A - The fundamental principle of coherent control, realized with the two-photon transition s→ 5sin sodium; B - The data for fluorescence maximization on the left and minimization on the right femtosecond pulse shaping

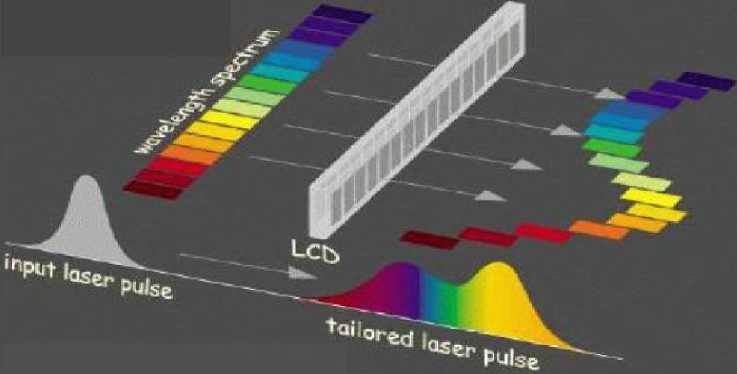
Figure 2: Experimental versatility of light

Researchers are also beginning to look beyond the goals of manipulating micro-world events as the prime objective. Many of the fundamental contributions of the subject may arise from the finessed quantum manipulation of molecules producing a unique source of data to learn more reliably about the most intimate atomic-scale interactions. Coherent molecular motion depends sensitively on intramolecular forces, and this sensitivity is reflected in the detailed structure of the experimental data. Observations of such dynamics should be a rich source of data for inversion to learn about interatomic forces.

This review explores issues relevant to molecular control through an expression of the current state of the field, an enumeration of desired physical objectives, and an assessment of the techniques necessary to meet the objectives. As a preview of the expansion of the coherent control field through the use of ultrafast laser pulses, the main focus is on the issues and techniques that need attention for the creative evolution of the subject.

• B.    Physical-Chemical Quantum Control Objectives . There are two general reasons for considering coherent control of quantum phenomena: first , to create a particular product that is unattainable by conventional chemical or photochemical means and, second , to achieve a better fundamental understanding of atoms and molecules and their interactions. With these goals in mind, many two-pathway experiments and some pulse control studies have been successfully applied in a variety of quantum systems. Two-pathway experiments have established the validity of the underlying principles and are capable of achieving effective control in appropriate circumstances. However, the number of possible control objectives and systems open to two-pathway control appears limited, compared with what may be attained through the coherent manipulation of quantum dynamics by means of ultrashort pulses.

Current experimental and theoretical studies suggest that large classes of molecules may be brought under coherent photodissociative control, but the possibility of chemical production by this means may remain elusive for a variety of reasons, including merely the cost of the photons per mole involved. Many other molecular applications are also worthy of pursuit, including the cooling of molecules to very low temperatures with tailored laser fields. Besides the objectives of creating unusual products and molecular states, the interrogation of the ensuing coherent dynamics may provide a new class of data with special capabilities for learning about atomic and molecular interactions (see below). Many laboratory techniques and theoretical concepts will need to be interactively incorporated for coherent control to be broadly successful.

• C.    Theoretical Design of Quantum Controls . Theory is playing a major role in conceptualizing the principles of coherent control, as well as providing designs for the control fields to manipulate molecules in the laboratory. Except for the simplest applications, intuition alone as a means of coherent control "design" generally will fail because the manipulation of constructive and destructive quantum wave interferences can be a subtle process. At the other extreme is the application of rigorous optimal control theory design techniques that can find the best way to achieve the molecular objective by manipulating interferences. The procedure is to iteratively solve the Schrödinger equation describing the molecular motion and thereby to optimize the form of the laser field so as to best meet the molecular manipulation objective.

Until now, control field design has largely focused on numerical explorations of possible control fields and associated algorithms to accelerate the design process. Special challenges include finding designs in the intense field regime and for cases in which incoherence effects occur because of molecular collisions or spontaneous radiative emission. The goal of optimal control is to provide laser designs for transfer into the laboratory to implement with the molecular sample. The ability to obtain high-quality laser control designs is hampered by the lack of complete information about the interatomic forces and the computational challenges of solving the nonlinear design equations. Therefore, an increased emphasis is being placed on providing control field estimates whose application in the laboratory would at least give a minimal signal in the target state for refinement of the closed loop, as described in the next section.

• D.    Quantum Learning and Feedback Control . A significant advance toward achieving control over quantum phenomena was the suggestion to introduce closed-loop techniques in the laboratory. The need for such procedures stems from the inability to determine reliable laser control designs, especially for polyatomic molecules. There are two general forms of laboratory closed-loop controls: learning control and feedback control. Learning control involves a closed-loop operation where each cycle of the loop is executed with a new molecular sample; feedback control follows the same sample from initiation of control to the final target objective. These two incarnations have distinct characteristics.

Figure 2 shows experimental versatility of light (frequency domain pulse shaping using AOM’s or LCD’s for both amplitude and phase available in VIS, near-IR).

The overall components of closed-loop learning control in quantum systems are depicted in Figure 3.

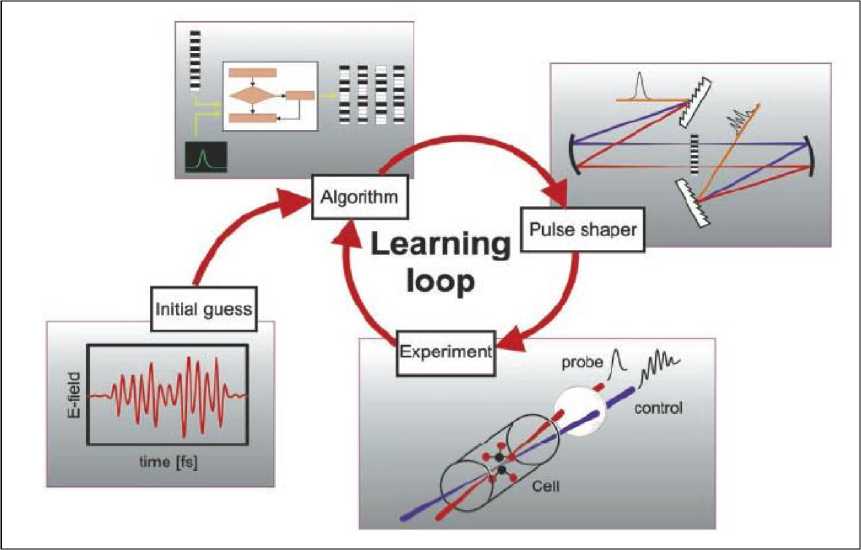
Figure 3. A closed-loop process for teaching a laser to control quantum systems

Remark . The loop is entered with either an initial design estimate or even a random field in some cases. A current laser control field design is created with a pulse shaper and then applied to the sample. The action of the control is assessed, and the results are fed to a learning algorithm to suggest an improved field design for repeated excursions around the loop until the objective is satisfactorily achieved. The procedure generally involves three elements: ( i ) an input trial control laser design, ( ii ) the laboratory generation of the control that is applied to the sample and subsequently observed for its impact, and ( iii ) a learning algorithm that considers the prior experiments and suggests the form of the next control for an excursion around the loop once again, and so on. If the molecular control objective is well defined, the control laser of appropriate capability, and the learning algorithm sufficiently intelligent, then this cyclic process will converge on the objective. In some cases, a quasi-random field might be used (that is, the investigator goes in blind) to first detect an initial weak signal from the product molecule for further amplification. In especially complex cases, it may be necessary not only to detect the product but also to observe critical intermediate molecular states in order to efficiently guide the closed-loop process toward convergence. It should be noted that the laser field need not be measured in this learning process, as any systematic characterization of the control "knobs" will suffice. This procedure naturally incorporates any laboratory constraints on the controls, and only those pathways to products that are sufficiently robust to random disturbances will be identified. Full computer control of the overall process is essential, as the loop may be traversed thousands of times or more in order to converge on the molecular objective. A variety of learning algorithms may be utilized for this purpose, presently genetic-type algorithms are being employed, although others have been considered in simulations. More attention needs to be given to the nature of these algorithms and, especially, their stability in the presence of laboratory disturbances. Typical quantum control objectives are expected to have multiple successful laser control solutions, and it is to be hoped that at least one may be found in the learning process.

• E.    Toward Combinatorial Laser Chemistry . Recent experiments with closed-loop learning control have been successful going in blind for the manipulation of fluorescence signals, photo-dissociation products, and other applications.

An illustration of photo-dissociation control is shown in Figure 4.

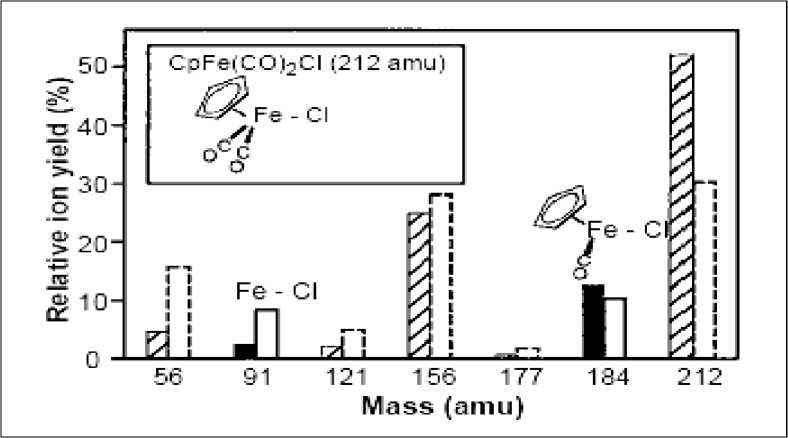
Figure 4. The controlled fragmentation of CpFe(CO)2Cl achieved with a femtosecond laser pulse shaped in a phase modulator

Remark . The ratio of FeCl1 (mass 91) to CpFeCOCl1 (mass 184) production is either maximized (black bars) or minimized (white bars) by the use of the closed-loop learning process depicted in Figure 3.

The Figure 4 also shows additional uncontrolled fragments from the molecule as dashed. In this case, the objective was to break selected bonds of the CpFe ( CO ) Cl molecule (here, Cp denotes the cyclopentadienyl ion) by either maximizing the product COCl ⁺ / FeCl ⁺ branching ratio (Figure 4, black bars) or alternatively minimizing the same ratio (Figure 4, white bars). A distinct optimal laser field was found for each of the two processes with laser phase modulation techniques, guided by a genetic learning algorithm. Experiments such as these could be referred to as combinatorial laser chemistry, by analogy with similar quasi-random chemical synthesis techniques. It is expected that the successful control of virtually all quantum dynamics phenomena, especially of a complex nature, will require the use of closed-loop learning techniques.

By repeatedly starting with a new molecular sample, learning control sidesteps the issue of whether the observation process may disturb the subsequent evolution of the quantum system. In contrast, feedback control would work with the same quantum system from time of control initiation through evolution to the final state. In some cases, feedback might be introduced for reasons of stabilization around a nominal operating condition, as perhaps, in a quantum computer. Limitations on the speed of electronics and the manipulation of general electro-optical elements suggest that quantum feedback control experiments will likely apply to systems having long natural time scales. Overall, a diagram similar to that in Figure 3 is also operative for quantum feedback control; however, some distinct differences exist.

First, the feedback algorithm must operate with sufficiently reliable knowledge of the system Hamiltonian to make good judgments on the subsequent controls while the quantum system is still continuing to evolve. Second, a clear competition exists between the desire to use the control algorithm to get as much information as possible about the evolving state of the quantum system, and the fact that gathering ever more precise information will increasingly disturb the system and lead to a larger degree of uncertainty about its control. Although some mathematical analysis of feedback control has been considered, the practical feasibility of quantum feedback control remains an open question, especially for cases involving many cycles around the control loop. As a first step toward feedback experiments, the continuous observation of an evolving quantum state has been made. For control objectives that are not overly demanding, it is possible to consider the performance of observations that minimally disturb the system. An example might be the control of a Bose-Einstein condensate cloud of atoms where weak observations of only a scattered few atoms should be sufficient to characterize the control of the overall spatial features of the cloud. Molecular motion is also often semiclassical, suggesting the existence of a broad class of feedback control behavior lying somewhere between the strict limitations of quantum mechanics and the less demanding situation found in classical engineering applications.

• F.    Laboratory Realization of Quantum Controls . The laboratory implementation of molecular control has been demonstrated with continuous wave lasers and, in the time domain, with ultrashort laser pulses. Although the use of continuous wave lasers is effective in some cases, in general, a few frequencies will not be sufficient to create the necessary interferences in complex problems where a number of quantum states have to be simultaneously brought into constructive superposition. Pulses, lasting less than 20 fs correspond to a bandwidth of about 1000 cm ^{- 1} , and, therefore, provide many independent laser frequency subcomponents that can be tuned simultaneously with a pulse shaper. Because no electronic device is fast enough to work on a femtosecond time scale, only frequency domain laser pulse-shaping is feasible. In the near-infrared ( IR ) spectral range, this technique is well developed for laser phase and amplitude modulation. Acoustic-optical modulators ( AOM ), as well as liquid crystal modulators ( LCM ), have been used for modulation, and LCM s are commercially available for the spectral range from 430 mm to 1.6 µ m .

The AOM combines the advantages of high spectral resolution and fast response times, but it also suffers from low transmission of the laser light (typically, 5% ) and more complex implementation. The LCM exhibits high transmission ( □ 80% ) and easy implementation, but it has low spectral resolution (typically, 128 discrete pixels) and slow response times of at least a millisecond. Fast response times are important for closed-loop laboratory optimization algorithms, as many thousands of distinct shapes need to be produced, along with repeated experiments for signal averaging.

Control of molecules in their ground electronic state is attractive for many applications, and for this purpose, it is necessary to develop pulse shapers that work in the mid- IR and far- IR spectral ranges. Breaking this problem down into parts, possibly around 3 µ m , 5 µ m , or 10 µ m , would allow for the manipulation of fundamental motions in many compounds (for example, the C - H stretch, and torsional and skeletal motions of organic molecules). Mid- IR femtosecond pulse energies of □ 10 µ J with temporal pulse lengths of □ 200 fs are already available, and they should be sufficient for pulse shaping and manipulation of highly excited molecular vibrations. The extension to longer wavelengths, improvement of tunability, and increased intensities, as well as the generation of very short femtosecond pulses in these spectral ranges, are all important for practical applications. The development of new types of nonlinear crystals already shows promising results in those directions. An open question concerns the ability to lock the phases of two laser pulses with different frequencies in order to coherently manipulate different vibrations in the molecule. The phase-locking would be inherent if it becomes possible to create ultrashort pulses in the IR .

The quality of current laser pulse-to-pulse stability appears to be adequate for many applications. The presence of modest noise can even help the search for a better solution in a complex multidimensional control field search with closed-loop laboratory learning algorithms. Certain applications (for example, quantum computation or those working in the high-intensity regime) may be more sensitive to laser fluctuations, and these cases need further evaluation.

• G.    Bulk Media Influences . The current molecular closed-loop control experiments have focused on the idealized situation of isolated molecules in a low-density gas or molecular beam. However, many important chemical, physical, and certainly biological processes take place in the condensed phase. Operating in this regime raises questions about the effects of the surrounding media on the coherent processes. These issues break into two categories of media effects on the molecules under control and on the propagating control field. All media effects may not be bad, as a molecule under control could benefit from the restraint of the atomic motion by the immediate surrounding medium, thereby providing partial dynamic guidance toward the target.

A naturally occurring example of this phenomenon exists in the photoisomerization of rhodopsin as a part of the visual process. In this case, the protein matrix in which the rhodopsin is embedded reduces the number of possible degrees of freedom for the outcome of the photoisomerization step to produce an efficient and selective visual excitation signal. On the other hand, the same media interactions may lead to the transfer of the controlled excitations of the target molecules to the media and a consequential loss of control. At present, little is known about these processes in the coherent control regime. Furthermore, the medium can influence the propagating laser pulse even in the gas phase, if the cell length is sufficiently long. A passing laser pulse will polarize the medium, which, in turn, can provide feedback and reshape the pulse even if there is no absorption.

This effect can be serious for control applications, as the delicate phase structure of the pulse is very important for quantum manipulation. However, theoretical studies have indicated the possibility of using laboratory learning control techniques to identify the laser pulses for transformation of the entire bulk medium as best as possible.

• H.    Quantum Control Rules of Thumb . With successful coherent control experiments now emerging in the gas and condensed phases, it is time to consider whether some consistent rules for achieving coherent control can be found. Chemistry operates with a relatively small number of rules, supported on a rational physical basis, prescribing the properties of a vast ever-growing number of molecules and materials. These rules serve to guide chemists in endeavors ranging from ab initio electronic structure studies to the synthesis of complex molecules. An open question is whether the domain of coherent control may similarly be reduced to a set of logical rules to guide successful manipulation of quantum phenomena. A comparison with traditional chemistry operating in the incoherent regime suggests that the new rules might be easily revealed owing to the more ordered conditions in coherent control. However, no such coherent control rules have emerged, except for the simplest notions of working with molecular absorption selection rules and spectral resonances in the weak field regime. Coherent control rules could be envisioned to range from the identification of common mechanistic pathways to characteristic control features associated with distinct classes of molecular objectives. Insight into this matter may be revealed by examination of the structure of the control fields, as well as consideration of the overall family of successful control solutions observed in the laboratory. Operating in the intense field regime opens up the prospect of making up the rules as desired, because the molecule and its electronic orbitals could be severely distorted at will. Seeking control rules of thumb also raises questions about how to categorize dynamic similarities and differences between molecules, as well as for control fields. Although an eventual lack of coherent control rules of thumb would not diminish the significance of the subject, establishing such rules would make the control of new systems easier to achieve. The best evidence for rules is likely to emerge only from the observed trends in the control of large numbers of chemical and physical processes.

• I.    Extracting Microscopic Information from Coherent Dynamics . In going beyond the use of molecular excitation for control purposes, the observation of controlled dynamics is also rich in information on the underlying interatomic forces. Learning about interatomic forces has been a long-standing objective in the chemical sciences, and extracting that information from observed coherent dynamics entails finding the appropriate data inversion algorithms for this purpose.

Various forms of continuous wave spectroscopy have been the traditional source of data for attempts at extracting intramolecular potential information. Although such spectra are relatively easy to obtain, serious algorithmic problems have limited their inversion to primarily diatomic molecules or certain special circumstances with polyatomics. This traditional approach has many difficulties, including the need to assign the spectral lines and to deal effectively with the inversion instabilities. As an alternative, coherent control techniques may be used to launch a molecular excitation to scout out portions of the molecule and to report the information back by probing with ultrafast lasers.

The second approach lends itself to arguments that experiments in the time domain may provide the proper data to stabilize the inversion process. These arguments generally reduce to the use of localized wave packets as a means of achieving stabilization. Although any single experimental observation would not yield global-scale molecular information, it may unambiguously identify a local region. It appears that the ultimate source of data with this goal in mind is "movies" of atomic motion obtained from ultrafast imaging techniques. A theoretical analysis indicates that such data would be ideal, as it admits an inversion algorithm with unusually attractive characteristics, including (i) no need to solve Schrodinger’s equation, (ii) a rigorously linear mathematical formulation calling for no iteration for data inversion, (iii) inherent stability arising from the imaging data explicitly defining the region of the potential that may be reliably identified, and (iv) no need to know the control pulse initiating the dynamics. Although it is early to speculate when such molecular movies of high resolution and quantitative accuracy will be available, these algorithmic considerations provide strong motivation for pushing in this direction. In addition, the utility of other types of coherent temporal data for inversion needs consideration.

Significant advances have been made in recent years toward establishing the broad foundations and laboratory implementation of control over quantum phenomena. Since its inception, this field has anticipated the promise of success just around the corner, but now, there are preliminary experimental successes. Another important new feature is the increasing breadth of controlled quantum phenomena being considered, and success in one area will continue to foster developments in others. A basic question is whether molecular control executed in the coherent regime offers any special advantages (such as, new products or better performance) over working in the fully incoherent kinetic regime. Answering this question should be a major goal for the field. However, even in cases where incoherent conditions are best, the same systematic control logic may produce better solutions than those attainable by intuition alone. Although creating unusual molecular states, or even functional quantum machines (for example, quantum computers), could have great impact, the ultimate implications for controlling quantum processes may reside in the fundamental information extracted from the observations about the interactions of atoms. The synergism of femtosecond laser pulse-shaping capabilities, laboratory closed-loop learning algorithms, and control theory concepts now provides the basis to fulfill the promise of CC. A large number of experimental studies and simulations show that it is surprisingly easy to find excellent quality control over broad classes of quantum systems. We now prove that for controllable quantum systems with no constraints placed on the controls, the only allowed extrema of the transition probability landscape correspond to perfect control or no control.

Under these conditions, no suboptimal local extrema exist as traps that would impede the search for an optimal control. The identified landscape structure is universal for all controllable quantum systems of the same dimension when seeking to maximize the same transition probability, regardless of the detailed nature of the system Hamiltonian. The presence of weak control field noise or environmental decoherence is shown to preserve the general structure of the control landscape, but at lower resolution.

K. Quantum Optimally Controlled Transition Landscapes. The control of quantum phenomena is garnering increasing interest for fundamental reasons as well as on account of its possible applications. In general, the redirecting of quantum dynamics is sought to meet a posed objective through the introduction of an external control field C (t) , often expressed as a function of time and frequently being electromagnetic, arising from laser sources. The field of optimal control theory ( OCT ) has arisen for the design of controls in simulated systems, and the ultimate interest lies in executing optimal control experiments ( OCEs ). By employing closed-loop learning control techniques, the number of such experiments is rapidly rising. At this juncture, there are many OCT studies exploring the control of broad varieties of quantum phenomena, and OCEs have similarly addressed several types of physical situations, including the selective breaking of chemical bonds the creation of particular molecular vibrational excitations, the enhancement of radiative high harmonics, the creation of ultrafast semiconductor optical switches, and the manipulation of electron transfer in biological photo synthetic antenna complexes. Applications to other areas can also be envisioned, including quantum information sciences. Typical OCT and OCE studies involve the manipulation of tens or even hundreds of control variables corresponding to the discretization of the control C (t) in either time or the analogous frequency domain representation. Almost all of the OCT design calculations use local search algorithms seeking an optimal control C (t) , whereas the current laboratory OCE applications have all used global genetic-type algorithms. In the case of OCT , a very striking result is that all of the calculations are generally giving excellent-quality product yields. In the case of OCEs with laser controls, the absolute yields are not known, although a basic finding is the evident ease of discovering control settings that can often dramatically increase the desired final product.

The above observations suggest that it is relatively easy to obtain good, if not excellent, solutions for quantum optimal control problems while searching through high-dimensional control variable spaces. Viewed as a generic optimization problem, this behavior is surprising. In the case of OCT , it is especially enigmatic because local algorithms virtually always seem to give excellent results. It is known that many and possibly a denumerable infinite number of control solutions may exist throughout the control search space, with the general belief that few of the solutions would be of high quality. Under these collective conditions, finding a poor quality local control solution would be the expected outcome of an optimal search for C ( t ) . The reason for this behavior must lie in some generic aspects of controlled quantum dynamics, rather than in the details of each particular problem, because the favorable findings are occurring for the control of all aspects of quantum dynamics phenomena.

In laboratory OCE implementations, many less-than-ideal circumstances may arise, including the system being at finite temperature, the presence of environmental decoherence, constraints on the controls, control field fluctuations, and observation noise. In contrast, most of the OCT design calculations have been carried out under ideal conditions where these problems do not exist. Because the problematic circumstances in the laboratory can in principle be improved on through better engineering and operating conditions, we primarily examine the ideal limiting case here. Some of the issues associated with less-than-ideal laboratory conditions will be returned to at the end of the report.

Although quantum control applications can span a variety of objectives, most of those currently being explored correspond to maximizing the probability p^ у = | u^| for making a transition from an initial state | i^ to a desired final state fj.. Here, U^ = ^ i|U|f ^ is a matrix element of the unitary time evolution operator U = U ^ C ( t ) J, which is a functional of the control C ( t ) . The operator U captures all of the controlled evolution over the time interval 0 <  t <  T out to some finite target time T . The physical goal is to maximize p_^ with respect to the control C ( t ) . Little is known about the mappings C ( t ) ^ U , which are generally highly complex. The analysis below is general insofar as it requires no knowledge of the particular system or its Hamiltonian, except specification of the general criteria that the system is controllable for some time T . We restrict ourselves to systems with a finite number of quantum states N , because the criteria for controllability have been established for this condition. Full controllability implies that at least one control field C ( t ) exists such that the result p ^у = 1 corresponds to an extremum

5pi . / 5C (t)

= 0

for all time 0 <  t <  T . It is evident that the transition probability is bounded by 0 <  p ^у <  1 , and we explore the control landscape p^ у ^ C ( t ) ^ as a functional of C ( t ) by considering the nature of all of the extrema satisfying Eq. (1). The control C ( t ) is allowed to vary freely without being constrained such that all extrema of P satisfy Eq. (1). Full controllability assumed as a basis for the analysis below does not preclude the existence of undesirable sub-optimal solutions satisfying Eq. (l) with p ^у <  1 at the extrema. We stress that an optimality analysis is distinct from a controllability assessment, which seeks only to establish the existence of at least one control that can exactly attain the target and generally reveals nothing about the nature of optimality (that is, the extrema of the optimal control landscape).

The distinction between controllability and optimality is also evident in their formulations: Controllability involves no notions of examining a landscape and its extrema, whereas optimality typically relies on seeking extrema regardless of the controllability of the system. At this juncture in the development of quantum control, essentially nothing is known about the nature of the control landscapes. We aim to reveal the general structure of the landscapes encountered when searching for optimal quantum controls.

In order to explore the landscape extrema, it is convenient to use the identity ii| U | f ^ = ( i | exp ( iA )| f ), where A ^ = A is an arbitrary N x N Hermitian matrix. Thus, Eq. (1) may be rewritten as

5 P . f  У ⁵ H f S A

sc (t)  » a:„  sc (t)

The mapping C (t) ^ A will be equally as complex as the original mapping C (t) ^ U for most applications, and the replacement of U by exp (iA) does not at first appear to facilitate the analysis. However, the assumed controllability of the system implies that each of the matrix elements Apq ^C (t)^ of A must be independently addressable while still preserving the Hermiticity of A , Thus, each element Apq [C (t)] should have a unique functional dependence on C (t) . These points in turn imply that the set of functions {SA^ / SC(t)} for all p and q will be linearly independent over 0 < t < T , and the only way that Eq. (2) may be satisfied is to require that d Uif Г _ d

^{9 A}pq     ' ^Apq

К i | exp ⁽ A )| ^f |²

(3a)

, d U_lf     d U

= U* — + Uif^i- = 0 i ^f dA       if d A

(3b)

pq            pq for all p and q . The relation in Eq. (2) is now replaced by the Hamiltonian-free generic form in Eq. (3), which has sidestepped the need to solve the Schrödinger equation and the system optimality can be analyzed from the kinematics of an arbitrary Hermitian A . This transformation reduced what appeared to be a highly complex system-specific analysis of Eq. (1) to a generic analysis for any controllable quantum system.

A detailed examination of Eq. (3) leads to the conclusion that

U_v = exp ( ia )

where a is a real phase such that | U ^. | = 1. The analysis started with the implicit assumption that | U ^. | ^ 0, although the possibility | U ^ | = 0 can certainly arise for nonzero control fields. Thus, all of the quantum control landscape extrema satisfying Eq. (1) take on the value

searching for effective quantum controls. The result in Eq. (5) was also confirmed by numerically solving the optimality equations for a number of cases of dimension N up to 10, and in all cases only perfect solutions were found.

The surprising conclusion in Eq. (5) is that under the simple assumption of controllability, the only extrema values for quantum optimal control of population transfer correspond to perfect control. Recall that optimality and controllability are distinct concepts, with the latter generally not precluding extrema with values of P^ ^ <  1 . Thus, quantum control of P ^_z has the unusual highly attractive behavior that there are no less-than-perfect, suboptimal local extrema to get trapped in when searching for an optimal control. This result immediately explains the general finding across virtually all of the hundreds of literature OCT studies that easily identified excellent control solutions. The analysis here does not reveal the multiplicity of solutions, but many distinct controls corresponding to individual extrema in Eqs. (2) or (3) are likely to exist in any application.

Practical control landscapes are in very high dimensions, because the control C ( t ) is typically represented in terms of many variables for adjustment. Nevertheless, the essence of the landscape may be captured by the sketch in Figure 5, just considering two of these variables denoted as x and x .

Any optimal control study always starts with an initial trial control, and the figure indicates that regardless of that trial choice, the nearest optimal solution will always be perfect. Each trial solution will always start out on an upward slope toward a control C ( t ) giving perfection, p ^^ = 1 . However, the character of the search for such solutions can depend on the algorithm used, and the nature of the solutions can be quite distinct. A very sharp extremum, as at point A , would not be robust to small control field variations and likely difficult to discover with algorithms inevitably taking finite steps. Similarly, searching in the vicinity of a group of such narrow non-robust solutions, as around domain B , could easily lead the search into exhibiting fibrillation behavior as it jumps from one local environment to another, taking on rather arbitrary P values without achieving convergence.

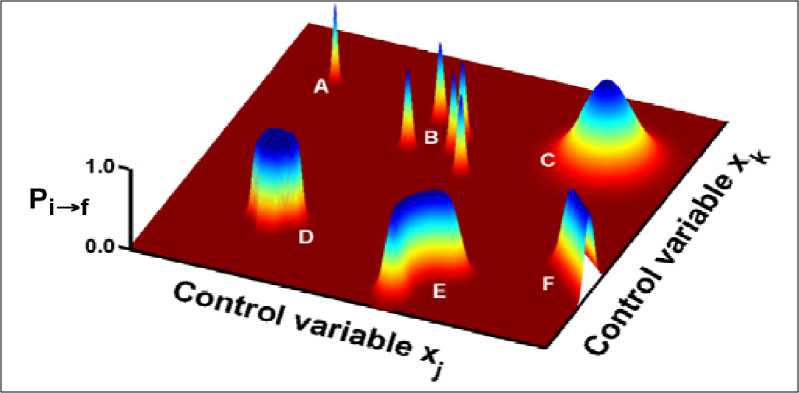
Figure 5. The general behavior of the quantum landscape for the probability P

Solutions of the type around point C would be easy to find because of their broad and rapidly attracting character. However, solutions of the type around point D are more robust to control variations and are the most attractive for discovery. Other extrema might exhibit partial robustness to one or combinations of the control variables as indicated by a solution of type E or F . Finally, the optimum near F at the edge of the depicted domain serves to point out that the control space is of arbitrary extent, and solutions may exist anywhere. These arguments fortunately also imply that finding robust control solutions will be easier than finding non-robust ones.

The qualitative behavior depicted in Figure 5 and the analysis leading to Eq. (5) explains the seemingly puzzling observation of increasingly successful OCT and OCE results while searching through high dimensional spaces of control variables. Naturally, a variety of issues in the laboratory, including the lack of total controllability, the presence of field fluctuations, noise in the observations, the initial state being statistically distributed, the presence of decoherence, and constraints on the controls would all cloud the strict conclusion in Eq. (5) which is valid under ideal conditions. It is beyond the scope of this report to delve into the intricate issues involved with these points, but some comments are warranted to place the present work in the context of the evolving OCE studies. First, less-than-ideal conditions could result in lowering the optimal yield to P_> < 1 and begin to introduce roughness (that is, local suboptimal extrema) in the control landscape. Perhaps the most important contributing factor to attaining less than perfect control is the fact that in all cases, the control is inevitably constrained in possibly many ways, including operating with a finite number of control variables of restricted range. The net result of constraints being placed on the controls can be a complex matter to assess, but numerical simulations show that field restrictions play an increasingly important role when approaching high yields (those greater than 0.8 ). The landscape of P revealed in the analysis above is independent of control restrictions, but access to certain regions of the landscape will be limited and the view of the landscape possibly distorted by field constraints. The latter behavior with constrained controls is likely the reason that typical OCT studies appear trapped in suboptimal, although generally still excellent, solutions. Finally, the use of various dynamical approximations (especially of a nonunitary nature) with significant errors could alter the landscape structure from that found here on general grounds.

The influences of field noise and environmental disturbances are generally complex matters to assess. A common and often reachable desire is to operate in the regime where these effects are weak; and in this case, a simple perturbation analysis may be carried out, providing a clear qualitative assessment of these effects on the control landscape. In the case of control noise, there will be an ensemble of similar controls {C_t ( t ) } , l = 1,2,... and the laboratory observable will be an average PP_f = pi^/) over the ensemble { C _z} . Here, P is the original landscape with sharply defined perfect features (as characterized in Figure 5). If the noise is weak, then its influence will be to act as a filter providing a lower resolution view Pⁿ of the original landscape P . This filtered view will most strongly affect the non-robust solutions, such as at A and B in Figure 5, by significantly reducing their value. In contrast, the desirable robust landscape features (solutions) at C and D should be little affected.

Weak decoherence will have a similar influence. In this case, the "system" still has N states, including | 0 and | / }, but there is additionally a set of "bath" states { ^ }. The standard view of decoherence is to average over the initial probability density p of bath states, where ^_b p = 1 and sum over all final bath states to give the observation of interest as pd^_f = ^^ _yp_bP_b^^ . For a fixed desired system transition | i ) ^ | f ) , there will be a landscape P^^ like that in Figure 5 for each pair | b ) and | b ') of bath states. With an environmental bath weakly coupled to the system, it is natural to assume that the family of landscapes P are all similar, and the summation above will again give a lower resolution view P^dec of the nominal sharp decoherence-free landscape. The net outcome is then the same as with weak field noise.

Cases of strong field noise and decoherence could easily greatly distort the landscape, but these are conditions to be avoided if possible, because much of the power of quantum control would be lost in this regime. Thus, the results in Eq. (5) provide the basis to expect that high-quality quantum control should be easily attainable under reasonable circumstances. The work shows that as laboratory conditions approach the ideal limit, the landscape is devoid of false traps in seeking to make a transition | ^ ^ | f^ .

The establishment of the main results in this case arose from separating the very complicated functional dependence of p^^C ( t ) ^ upon C ( t ) into a two-step analysis of ( z ) A_pq ^ C ( t ) J and ( zz ) d( z | exp ( iA )| f / / d A_pq . Step ( i ) still involved an equally complex functional mapping of the control field in A ^ C ( t ) J ; this difficult aspect of quantum control to unravel, which is application-specific, was put aside by just drawing on the uniqueness of each functional mapping A_pq ^ C ( t ) ^ for all p and q . In this fashion, the analysis reduced to examining step ( и ) through the kinematical structure in Eq. (3), which was thoroughly decomposed. Our findings sharply contradict the intuitive expectation that the typically highdimensional quantum control search spaces would generally contain suboptimal solutions. A further surprising result is the generic nature of the landscape topology deduced by the kinematic analysis. When seeking to maximize the transition | z ^ ^| f^ for a controllable system of dimension N , the landscape structure is invariant to the choice of i and f as well as any details of the Hamiltonian. Differences in search behavior over the landscape can in practice arise due to the particular nature of the Hamiltonian and the control. Nevertheless, the optimal control landscape topology identified in this work is universal (more details se in review articles [1, 2]).

Example : Computing with dancing molecules ( or mathematics makes molecules dance ). An orchestrated dance of molecules (see, Figure 6) could be made to represent logic necessary for several simultaneous computation processes.

Such motion of the molecules is described by Quantum Mechanics and the resulting computation as quantum computation. This new approach to computing promises to revolutionize the present computing capability and can be implemented through light-matter interactions. Logic implementation through light brings in the possibility of distributiveness for large scale computing.

Figure 6. Dancing molecules in a laser field

Remark. The desire to understand and control chemical reactions can be traced to the origins of civilization. Modern scientists have succeeded in extending their investigations of the control of natural processes into the microscopic domain; ever greater precision and selectivity are required to meet the resulting challenges. These challenges include the control of molecular motion and bonds in the synthesis of new molecules and materials, the control of quantum states of atoms and molecules for the development of quantum computers, the control of nonlinear optical processes, and the control of quantum electronic motion in semiconductors. As laboratory experimentation becomes more and more difficult, theoretical chemists and physicists are using highly sophisticated mathematical models and simulations of the microscopic world with the aim of guiding the refinement and design of quantum control experiments.

In this example we examine (a) the ways in which mathematical models and techniques have been employed by these theoreticians and (b) the future of this relatively young area of research, known as quantum mechanical control.

The problem of quantum decoherence has also been a long-standing issue in the control of quantum systems, and research over the past years have shown how ultrafast optically shaped pulses can control quantum decoherence in a molecular system (see, Figure 7).

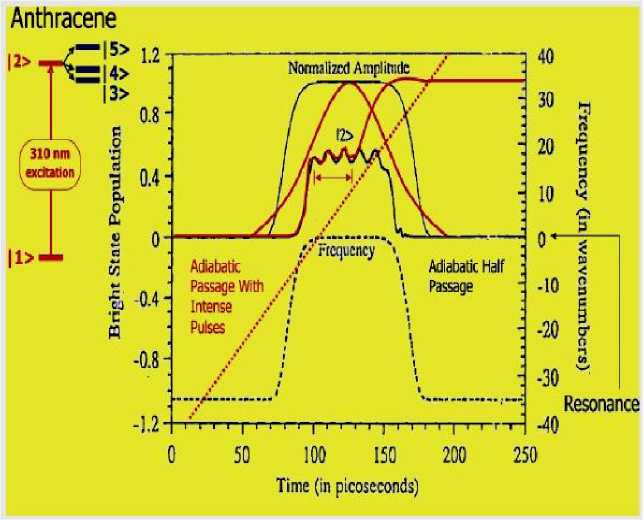
Figure 7. Control of decoherence as demonstrated for a model based on Anthracene molecule fluorescence studies with different shaped pulses

Such pulses induce “adiabatic following” of the excited state population and avoids decoherence for the period of the pulse. Ultrafast pulse shaping has evolved slowly along with the technological progress and only now truly arbitrary pulse shapers with fast update rates have become available. Transmission of short pulse through any propagating medium invariably distorts both the phase and amplitude of the pulse.

Ultrafast pulse shaping promises to correct such propagation distortions (see, Figure 8).

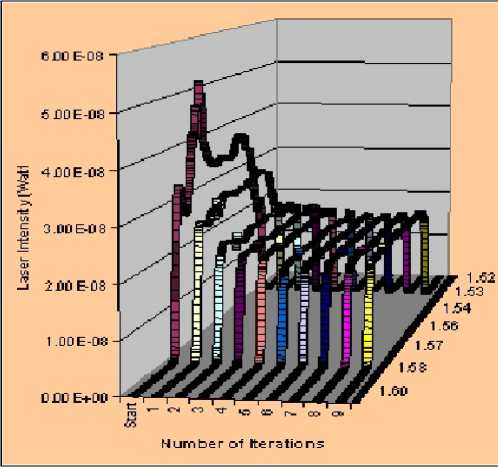
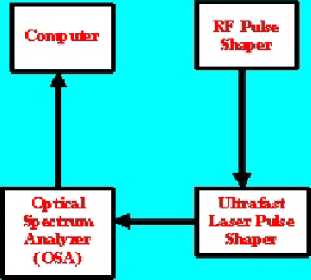
Figure 8. Demonstration of feedback-loop controlled AOM pulse-shaping scheme to achieve desired pulse shapes or to correct for undesirable pulse shape distortions. Here a rectangular pulse shape was desired, which is achieved after nine iterations from a distorted starting pulse. The optimization scheme used is shown alongside.

Remark . The pulses can be shaped before launching into the fiber to correct distortion as it propagates through optical fiber channels by applying precise amount of negative distortion to obtain the desired pulse. Thus long distance transfer of information via shaped pulses becomes possible. These corrected pulses could contain sequences of steps that would result in performing quantum computation. So, in essence, what we would achieve is packet containing steps to execute quantum computing.

The present research aims in exploring the possible ultrafast pulse shaping technique that could be adapted to achieve distributed QC. This will also help in increasing the speed of quantum logic gate operations through terabit/sec communication.

Let us now to discuss quantum mechanical model of this molecular control.

Quantum Mechanical Models

Molecular control is an inverse problem that can be analyzed with quantum mechanical models (see, Figure 9).

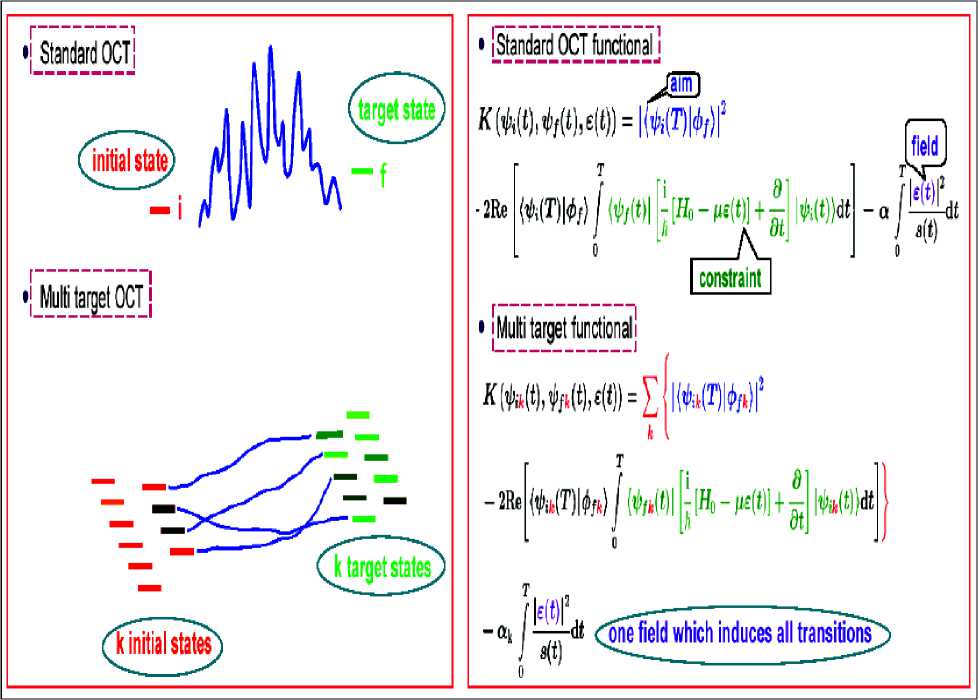
Figure 9. Background of optimal control theory (OCT)

Given molecular objectives (e.g., a specific quantum mechanical state), determine an optical field that, when applied, would lead to the objective. (Existence of the field does not guarantee uniqueness. In fact, the number of possible fields is usually infinite; scientists proceed by determining a field that can be produced easily in the laboratory at relatively low cost, which leads to the desired objective efficiently.)

Herschel Rabitz and his colleagues at Princeton University (see, Figure 10) formulated the molecular control problem mathematically as follows: Determine a field 8 ( t ) that minimizes the optimizing functional

Figure 10. Chemistry professor Herschel Rabitz is a pioneer in the field of molecular control

J ( ⁸ ) — J 0 + J p + J , d + J_c ,0 ,

5J (8)

by requiring that --- — 0 . Here, J _o represents the physical objectives, J the penalties and ancillary

68                0                                      p costs, J the dynamic constraints, and J the objective constraints. Each of the terms on the right-hand side depends either explicitly or implicitly on 8 (t) , and they compete to be simultaneously minimized.

The terms J and J of the optimizing function depend on the physical objective(s) of, and the penalties associated with, the control problem, and their formulation is chosen by the designer. For example, if the objective is for the operator O ˆ to have a specified expectation value O at time t = T , then a choice for J ₀ would be J _o — ( ^ ( T )| O| у ( T )^ - O ) . When the expectation value equals the target O , the objective term J _o is minimized and the state of the system at time T will depend on the field 8 ( t ) for all times 0 <  t <  T . The choice of J _o is not unique; the example given here, which is reasonable and simple for computations and analysis, was chosen to illustrate how designers introduce objectives. The penalty term J can be expressed as the expectation value of an operator O ‘ with a weight function W ( t ) such that

J p

—Jdt • Wp(t ).| у(t )l °) 'I у(t)) 12

Suppose, for example, that O = H is the i-th localized piece of the Hamiltonian, corresponding, for example, to the desire to maximize energy associated with the i-th bond. A simple choice for O' is then о' = H - Hi =S Hj- j * i

Another penalty term commonly considered is the optical field fluency

T

Jp = J dt ■ W8 (t )■ ^2 (t), where We (t) is a weighting function. The fluency, which is a measure of the energy in the control field, can be modified to weight against electric fields larger (-) or smaller (+) than 8* (t) by replacing the integrand with W (t)■ 82 (t)■ H|8(t)±8*J where H[□] is a Heaviside function. To bias against undesirable frequency components, Rabitz et al. suggest the use of a penalty term associated with frequency filtering, ^

such as J_p = J d ^ ^ W_s ( ю ) 1 ² ( ю ) , where W_s ( to) is a spectral weight and I ( to) is the Fourier transform -^

of 8 ( t ) .

A simple term for guaranteeing consideration of robustness to control field errors in a system is the sensitivity penalty function

S O ( T ) 58 ( t )

T

^J P = J ^dt"

where O ( T ) is the quantum mechanical expectation value. This penalty term monitors a system and favors greater control by reducing the impact of field fluctuations on the target O ( T ) .

A dynamic constraint term J for a quantum mechanical model has the form

T

Jc, d =J dt W t )| ih 77-H (t )| v (t)}-c c , 0              d t where Я(t) is a Lagrange multiplier function, H (t) is the time-dependent Hamiltonian, and c.c. denotes the complex conjugate (to ensure that the control field is real).

If the physical objectives for the term J must be satisfied exactly, Rabitz et al. suggest the use of an objective constrain term Jc o = n ^O (T) - OJ , where n is a Lagrange parameter. In our earlier analysis, the terms J and J are used as a means to quantitatively balance the tradeoff between the objective and penalties and do not guarantee the arrival at user-specified expectation values. In general, use of the objective constraint term J places heavier demand on the system and may result in less favorable characteristics or conditions for system control, e.g., relaxed satisfaction of the penalty terms J , such as those described above, or the need for a more intense external field. Unless an objective constraint term is necessary, use of a penalty term may be a better compromise for designing a control system. In the next step in the design of the external field £ (t) , the variation of the optimizing functional with respect to the unknown functions is computed to produce Euler equations. A simple example is given here to describe the procedure. Consider a quantum mechanical system with the Hamiltonian

H = H0 + ц£ (t), where Ho is the free molecular Hamiltonian and ц is a molecular dipole function. If the objective is to steer the molecule to the state ф , then the associated Euler equations are

- V ?= ^H ( t ^v ( t ) ^, v ( ⁰ ) = ^{v ;}

m^ = H ( t ) 2 ( t ) , 2 ( T ) = 2 [ ф-v ( T ) ]

£ ( t ) = Im

^ .

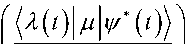
Eq. (6) is the Schrodinger equation for the wave function v ( t ) with an initial condition, Eq. (7) is the Schrodinger equation for the Lagrange multiplier function Л ( t ) with a specified condition at time T , and Eq. (8) expresses the field £ ( t ) in terms of these latter functions. The functions £ ( t ) , у ( t ) , and Л ( t ) are all unknown.

Remark . Determining a solution to the set of Eqs (6) – (8) is a nontrivial mathematical problem. The condition at target time t = T in Eq.(7) depends explicitly on the difference between the objective target state and the actual state of the system, which was produced by the designer field given by Eq.(8). In general, the existence of solutions is assumed. Since a closed-form solution to Eqs (6) – (8) usually cannot be found iterative techniques are used to determine a solution numerically. Tools developed by numerical analysts (e.g., spatial discretization schemes, basis set expansions, variational techniques, etc) are vital to the solution of the equations that arise in the design of controls for manipulating quantum systems.

The Power of Optimal Control Formalism

Chemists generally take a pragmatic approach to the issue of uniqueness. When a solution exists, there are often multiple (or even an infinite number of) optimal solutions, i.e., fields £ ( t ) , corresponding to v ( t ) of equivalent or at least physically acceptable quality. A control system designer will choose the field that is easiest and least expensive to produce in a laboratory, or that is least likely to produce unwanted side reactions or by-products. To illustrate the power of the optimal control formalism, Shi, Woody, and Rabitz examined a 20-atom, linear, harmonic molecular system (see, Figure 11a) in which radiation from the field £ ( t ) can enter only through bond 1 — between the first and second atoms. The objective is to stretch bond 19 — between the 19th and 20th atoms — at the opposite end of the molecule while minimizing the total fluency and disturbance in the remainder of the molecule.

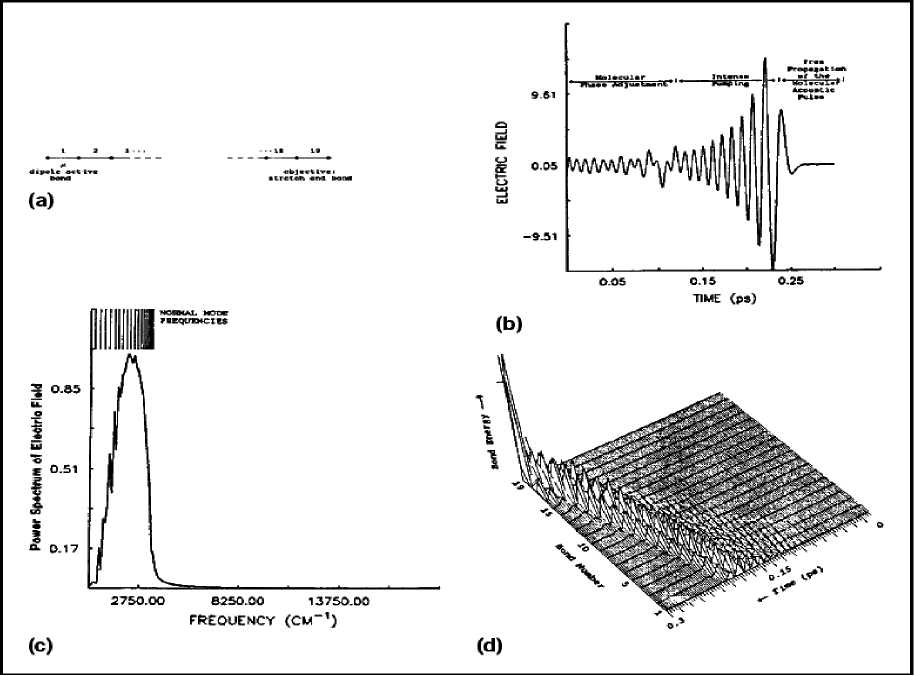
Figure 11. Linear chain bond-stretching objectives. (a) The 20-atom molecule with a dipole at one end and the objective of substantially stretching the bond at the other end at time t = 0.3 ps while minimally disturbing the remainder of the molecule. (b) The time-dependent electric field achieving the desired objective.

The time-varying electric field Б ( t ) leading to the objective, which was computed numerically, consists of three distinct periods: molecular phase adjustment, intense pumping, and free propagation of the pulse (Figure 11b). The graph of the frequency spectrum corresponding to the temporal pulse in Figure 11b shows that all modes of the molecule are simultaneously pumped by the field (Figure 11c). More specifically, higher-frequency normal modes are excited first, and lower-frequency modes last, to produce destructive interference during propagation of the energy along the molecular chain from bond 1 to bond 19 (Figure 11d). At target time t = T , all the waves arrive to form a coherent superposition at bond 19. Once the form of Б ( t ) is known, this intuitive explanation seems reasonable (and perhaps almost obvious); without prior knowledge of the solution, however, the mechanism defies guesswork.

The phase-adjustment period is central to the preparation of the entire molecule for the subsequent intense pumping, when most of the energy is deposited. Finally, the molecule signals that the radiative field should be turned off to allow for the transmission of the molecular excitation pulse from the energy-absorbing end of the molecule to the target bond at the other end. (c) The frequency spectrum corresponding to the temporal pulse in (b). The discrete normal mode frequencies are shown at the top. A highly broadband excitation is involved. (d) Localized bond energy as a function of time and molecular bond number. The coherent traveling excitation energy pulse is quite evident and results in a high degree of excitation at the end bond at the desired time. Follow-up studies indicate that it is possible to make the peak amplitude of the field, i.e., Б_шаx = max Б ( t ) , arbitrarily small by increasing the target time T .

o < t <  T

This information is valuable to designers of laboratory experiments; although low amplitude fields over long durations are desirable from a field-intensity perspective, they have an undesirable characteristic: Their coherence over long times require maintenance. Ultimately, laboratory experiments must be performed to determine which parameter settings are possible to implement and which will yield the best results.

Remark : Related works. In the late 1980s, Stuart Rice and David Tannor (then at the University of Chicago), Ronnie Kosloff (Hebrew University, Jerusalem), as well as Moshe Shapiro and Paul Brumer (Weizmann Institute of Science) developed a method that uses lasers to control the selectivity of product formation in chemical reactions. Rice and Tannor were among the earliest to consider a multiple-energy-level system. They use conjugate gradient methods to direct the convergence of a variational approach, like that described earlier, in their simulation studies. Around the same time, G. Huang, T. Tarn, and J. Clark presented an existence theorem for the complete controllability of a class of quantum mechanical systems. The theorem demonstrates that it is possible, in principle, to devise a scheme to control systems with a discrete spectrum so that 100% of a desired final state will be occupied in a finite number of steps. Because the existence proof is not constructive and does not provide a general scheme that can be used to direct reactions, plenty of work is left for experimental designers. The theorem also points the way to a broader area of research, i.e., existence proofs and algorithms for the control of open quantum systems. Several independent research teams have also used numerical simulations to study simple models of vibrational amplitude control, rigid molecular rotor control, transitions between molecular eigenstates, and bond-selective dissociation. These examples are drawn from the framework for the optimal control of quantum mechanical systems proposed for more general contexts by A. Butkovskii and Yu.I. Samoilenko. A direct implementation of the variational design procedure corresponds to open loop control. A laboratory venture of this type could work for simple cases (as has been demonstrated), but it is fraught with difficulties for most realistic laboratory systems, which are more complex. Judson and Rabitz have suggested the use of learning control techniques to circumvent problems associated with open loop control and to take advantage of the high-duty cycle of current pulsed lasers. In practice, a control design would be performed and refined iteratively in the laboratory. For full implementation of the process, stable learning algorithms, capable of operating quickly and reliably with quantum systems, must be identified.

Development of effective and inexpensive systems for molecular control is an exciting and potentially lucrative area of research. Successful endeavors will undoubtedly involve teams of scientists from many different backgrounds who can work in unison and who can appreciate the work of their teammates. The advent of more powerful computers and computational algorithms in recent years is enabling theoreticians to conduct more realistic simulations, which are contributing to experimental and system design. As witnessed already in industrial labs, simulations can help reduce labor and material costs in the development of timely new technologies, and applied mathematicians are in a great position to continue to make an impact. Although it can’t be taken literally, “Making Molecules Dance” is a colorful and inspirational slogan for recruiting some of the brightest young minds.

Quantum control in bio-inspired and nano-technologies

Several nanoscale technologies appear to be 3 to 5 years away from producing practical products. For example, specially prepared nanosized semiconductor crystals (quantum dots) are being tested as a tool for the analysis of biological systems. Upon irradiation, these dots fluoresce specific colors of light based on their size. Quantum dots of different sizes can be attached to the different molecules in a biological reaction, allowing researchers to follow all the molecules simultaneously during biological processes with only one screening tool. These quantum dots can also be used as a screening tool for quicker, less laborious DNA and antibody screening than is possible with more traditional methods.

Also promising are advances in feeding nano-powders into commercial sprayer systems, which should soon make it possible to coat plastics with nano-powders for improved wear and corrosion resistance. One can imagine scenarios in which plastic parts replace heavier ceramic or metal pieces in weight sensitive applications. The automotive industry is researching the use of nanosized powders in so-called nanocomposite materials. Several companies have demonstrated injection-molded parts or composite parts with increased impact strength. Full-scale prototypes of such parts are now in field evaluation, and use in the vehicle fleet is possible within 3 to 5 years. Several aerospace firms have programs under way for the use of nanosized particles of aluminum or hafnium for rocket propulsion applications. The improved burn and the speed of ignition of such particles are significant factors for this market.

A number of other near-term potential applications are also emerging. The use of nanomaterials for coating surfaces to give improved corrosion and wear resistance is being examined on different substrates. Several manufacturers have plans to use nanomaterials in the surfaces of catalysts. The ability of nanomaterials such as titania and zirconia to facilitate the trapping of heavy metals and their ability to attract biorganisms makes them excellent candidates for filters that can be used in liquid separations for industrial processes or waste stream purification. Similarly, new ceramic nanomaterials can be used for water jet nozzles, injectors, armor tiles, lasers, lightweight mirrors for telescopes, and anodes and cathodes in energy-related equipment.

Advances in photonic crystals, which are photonic band gap devices based on nanoscale phenomena, lead us closer and closer to the use of such materials for multiplexing and all-optical switching in optical networks. Small, low-cost, all-optical switches are key to realizing the full potential for speed and bandwidth of optical communication networks. Use of nanoscale particles and coatings is also being pursued for drug delivery systems to achieve improved timed release of the active ingredients or delivery to specific organs or cell types.

As mentioned above, information technology has been, and will continue to be, one of the prime beneficiaries of advances in nanoscale science and technology. Many of these advances will improve the cost and performance of established products such as silicon microelectronic chips and hard disk drives. On a longer time scale, exploratory nanodevices being studied in laboratories around the world may supplant these current technologies. Carbon nanotube transistors might eventually be built smaller and faster than any conceivable silicon transistor. Molecular switches hold the promise of very dense (and therefore cheap) memory, and according to some, may eventually be used for general-purpose computing. Single-electron transistors (SETs) have been demonstrated and are being explored as exquisitely sensitive sensors of electronic charge for a variety of applications, from detectors of biological molecules to components of quantum computers. Single-electron transistor, or SET, is a switching device that uses controlled electron tunneling to amplify current. The only way for electrons in one of the metal electrodes to travel to the other electrode is to tunnel through the insulator. Since tunneling is a discrete process, the electric charge that flows through the tunnel junction flows in multiples of e, the charge of a single electron. (Definition from Michael S. Montemerlo, MITRE Nanosystems Group, and the Electrical and Computer Engineering Department, Carnegie Mellon University).

Quantum computing is a recently proposed and potentially powerful approach to computation that seeks to harness the laws of quantum mechanics to solve some problems much more efficiently than conventional computers. Quantum dots, discussed above as a marker for DNA diagnostics, are also of interest as a possible component of quantum computers. Meanwhile, new methods for the synthesis of semiconductor nanowires are being explored as an efficient way to fabricate nanosensors for chemical detection. Rather than quickly supplanting the highly developed and still rapidly advancing silicon technology, these exploratory devices are more likely to find initial success in new markets and product niches not already well-served by the current technology. Sensors for industrial process control, chemical and biological hazard detection, environmental monitoring, and a wide variety of scientific instruments may be the market niches in which nanodevices become established in the next few years.

Therefore, as efforts in the various areas of nanoscale science and technology continue to grow, it is certain that many new materials, properties, and applications will be discovered. Research in areas related to nanofabrication is needed to develop manufacturing techniques, in particular, a synergy of top-down with bottom-up processes. Such manufacturing techniques would combine the best aspects of top-down processes, such as microlithography, with those of bottom-up processes based on self-assembly and self-organization. Additionally, such new processes would allow the fabrication of highly integrated two- and threedimensional devices and structures to form diverse molecular and nanoscale components. They would allow many of the new and promising nanostructures, such as carbon nanotubes, organic molecular electronic components, and quantum dots, to be rapidly assembled into more complex circuitry to form useful logic and memory devices. Such new devices would have computational performance characteristics and data storage capacities many orders of magnitude higher than present devices and would come in even smaller packages.

Nanomaterials and their performance properties will also continue to improve. Thus, even better and cheaper nano-powders, nanoparticles, and nanocomposites should be available for more widespread applications. Another important application for future nanomaterials will be as highly selective and efficient catalysts for chemical and energy conversion processes. This will be important economically not only for energy and chemical production but also for conservation and environmental applications. Thus, nanomaterial-based catalysis may play an important role in photoconversion devices, fuel cell devices, bioconversion (energy) and bioprocessing (food and agriculture) systems, and waste and pollution control systems.

Nanoscale science and technology could have a continuing impact on biomedical areas such as therapeutics, diagnostic devices, and biocompatible materials for implants and prostheses. There will continue to be opportunities for the use of nanomaterials in drug delivery systems. Combining the new nanosensors with nanoelectronic components should lead to a further reduction in size and improved performance for many diagnostic devices and systems. Ultimately, it may be possible to make implantable, in vivo diagnostic and monitoring devices that approach the size of cells. New biocompatible nanomaterials and nanomechanical components should lead to the creation of new materials and components for implants, artificial organs, and greatly improved mechanical, visual, auditory, and other prosthetic devices.

Remark . Exciting predictions aside, these advances will not be realized without considerable research and development. For example, the present state of nanodevices and nanotechnology resembles that of semiconductor and electronics technology in 1947, when the first point contact transistor was realized, ushering in the Information Age, which blossomed only in the 1990s. We can learn from the past of the semiconductor industry that the invention of individual manufacturable and reliable devices does not immediately unleash the power of technology — that happens only when the individual devices have low fabrication costs, when they are connected together into an organized network, when the network can be connected to the outside world, and when it can be programmed and controlled to perform a certain function. The full power of the transistor was not really unleashed until the invention of the integrated circuit, with the reliable processing techniques that produce numerous uniform devices and connect them across a large wafer, and the computerized design, wafer-scale packaging, and interconnection techniques for very-large-scale integrated circuits themselves. Similarly, it will require an era of spectacular advances in the development of processes to integrate nanoscale components into devices, both with other nanoscale components and with microscale and larger components, accompanied by the ability to do so reliably at low cost. New techniques for manufacturing massively parallel and fault-tolerant devices will have to be invented. Since nanoscale technology spans a much broader range of scientific disciplines and potential applications than does solid state electronics, its societal impact may be many times greater than that of the microelectronics and computing revolution.

Nanotechnology and Computers

The history of information technology has been largely a history of miniaturization based on a succession of switching devices, each smaller, faster, and cheaper to manufacture than its predecessor (Figures 12 and 13).

The first general-purpose computers used vacuum tubes, but the tubes were replaced by the newly invented transistor in the early 1950s, and the discrete transistor soon gave way to the integrated circuit approach. Engineers and scientists believe that the silicon transistor will run up against fundamental physical limits to further miniaturization in perhaps as little as 10 to 15 years, when the channel length, a key transistor dimension, reaches something like 10 to 20 nm.

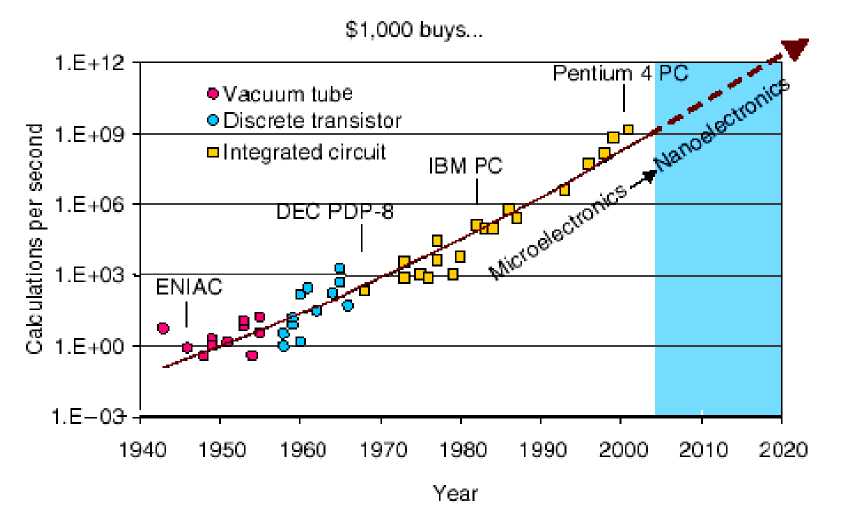
Figure 12. The increasing miniaturization of components in computing and information technology [Adapted from R. Kurzweil, The Age of Spiritual Machines, Penguin Books, 1999]

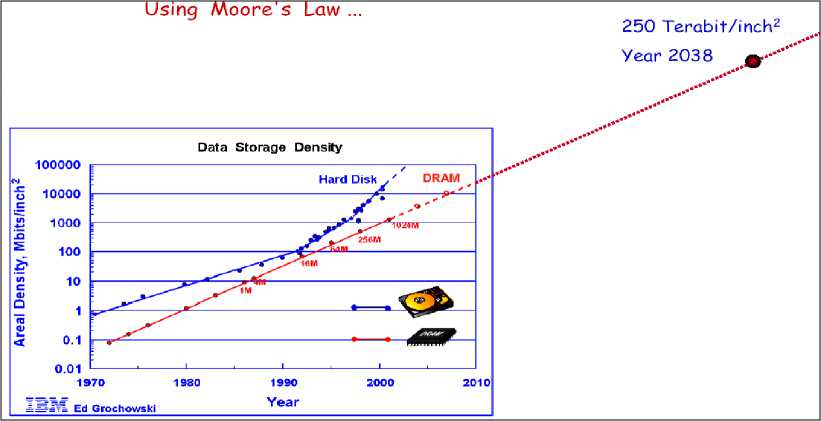
Figure 13. The increasing miniaturization of components in computing and information technology

Microelectronics will have become nanoelectronics, and information systems will be far more capable, less expensive, and more pervasive than they are today. Nevertheless, it is disquieting to think that today’s rapid progress in information technology may soon come to an end. Fortunately, the fundamental physical limits of the silicon transistor are not the fundamental limits of information technology. The smallest possible silicon transistor will probably still contain several million atoms, far more than the molecular-scale switches that are now being investigated in laboratories around the world. But building one or a few molecular-scale devices in a laboratory does not constitute a revolution in information technology. To replace the silicon transistor, these new devices must be integrated into complex information processing systems with billions and eventually trillions of parts, all at low cost. Fortunately, molecular-scale components lend themselves to manufacturing processes based on chemical synthesis and self-assembly. By taking increasing advantage of these key tools of nanotechnology, it may be possible to put a cap on the amount of lithographic information required to specify a complex system, and thus a cap on the exponentially rising cost of semiconductor manufacturing tools. Thus, nanotechnology is probably the future of information processing, whether that processing is based on a nanoscale silicon transistor manufactured to tolerances partially determined by processes of chemical self-assembly or on one or more of the new molecular devices now emerging from the laboratory. Let us consider general definitions and applications of nanotechnology based on quantum control.

Defining Nanotechnology

Nanotechnology is still in an early phase of advancement and is sometimes compared in the literature to information technology in the 1960’s and biotechnology in the 1980’s. Nanotechnology refers to the development and application of structures, materials, devices and systems with fundamentally new properties and functions which derive from their size in the range of about 1 to 100 nanometers (nm) (Siegel et al., 1999). It involves the manipulation and/or creation of material structures at the nanoscale in the atomic, molecular and supramolecular realm. At the nanoscale the characteristics of matter can be significantly changed, particularly under 10-20 nm, because of properties such as the dominance of quantum effects, confinement effects, molecular recognition and an increase in relative surface area. Downsized material structures of the same chemical elements change their mechanical, optical, magnetic and electronic properties, as well as their chemical reactivity, leading to surprising and unpredicted, or unpredictable, effects. In essence, nanodevices exist in a unique realm, where the properties of matter are governed by a complex combination of classical physics and quantum mechanics. At the nanometer scale, manufacturing capabilities (including by self-assembly, templating, stamping, ultra-precision engineering and fragmentation) are broad and can lead to numerous efficient outcomes.

Nanoscience is the result of interdisciplinary cooperation between physics, chemistry, biology, biotechnology, material sciences and engineering in studying assemblies of atoms and molecules. More than in other domains, nanotechnology requires the integration of many scientific, engineering and technical disciplines and competences. Applications of nanotechnology will penetrate and permeate through nearly all sectors and spheres of life (e.g. communication, health, labour, mobility, housing, relaxation, energy and food) and will be accompanied by changes in the social, economic, ethical and ecological spheres (see Figure 14).

Remark . As with other new technologies, nanotechnology evokes enthusiasm and high expectations: on the one hand, progress in science and technology, new productive applications and potential economic gain are envisaged; on the other hand, there are concerns about risks and unforeseen side effects (Roco and Bainbridge 2001 and 2005; Roco and Tomellini 2002). At the present time the assessment of the social, juridical and ethical consequences of nanotechnology relies more on hypothetical or even speculative assumptions than on rigorous scientific analysis (Hanssen and van Est 2004). Various science fiction scenarios and literary narratives have picked up nanotechnology as a major theme of their projections for the future. For example, the work of Eric Drexler (1986), which describes the scenario of self reproductive nanoengines, has been perceived to fall into the category of scientific “phantasy” (Iglhaut and Spring, 2003, p. 12). The novels of, inter alia, Anderson and Beason (1993), Stephenson (1996), Bear (2002), and Crichton (2002) use the example of nanotechnologies as a technical catalyst for their narratives. In arguably the most famous nanotechnology-related novel, “Prey”, Crichton (2002) describes a science fiction story in which swarms of nanotechnologically manufactured micro-robots, which he terms “Nanobots”, malfunction and attempt to conquer the world and destroy it. These novels use nanotechnology only as a carrier for more destructive technologies or for the misuse of human activities. Nevertheless, the link between nanotechnology and threatened human identity has been constructed in the mind of many intellectual observers.

NEMS Sub 50 nm structuring Ultra precision machining

Autonomous nanorobots Quantum point diode laser у-Ray _Optj_cg led gvM Photonic Cristals                   Analytics

BEC CNT composite materials CNT production Funcional surfaces

Self healing materials                        Dendrimers Nanoparticles/colloids

Magnetical fluids

Quantum point solar cells Nanostructured Dye solar cells hydrogen stores

Thermoelectrica                         Batteries Nano membranes

Precision mechanics/

Op tics/Analytics

Chemistry/ Materials

Energy/ Environmental Technologies

Waste water filter

Drug delivery Lab-on-a-chip systems Bio-chip arrays

Self organising systems          EUVL                             Flash-/DRAM

Optical (193nm) lithography

Medicine/ Life Science

Automotive

Invention phase Principle clarification

10-15 years

Technical realisation, Prototyping

5-10 years

Application Innovation

0-5 years

Broad usage Diffusion

Figure 14. Examples of Development Status and Application Fields of Nanotechnology (Courtesy: VDI Technologie zentrum, Germany)

Depending on the circumstances it can be expected that, over time, these associations will also penetrate public opinion.

The Promise of Nanotechnology

In 2000, the US National Science Foundation (NSF) estimated that $1 trillion worth of products worldwide would incorporate nanotechnology in key functional components by the year 2015 (Figure P.31; Roco and Bainbridge, 2001). The corresponding industries would employ about 2 million workers directly in nanotechnology, and about three times as many in supporting activities. These estimates were based on a broad industry survey and analysis in the Americas, Europe, Asia and Australia, and continue to hold in 2006.

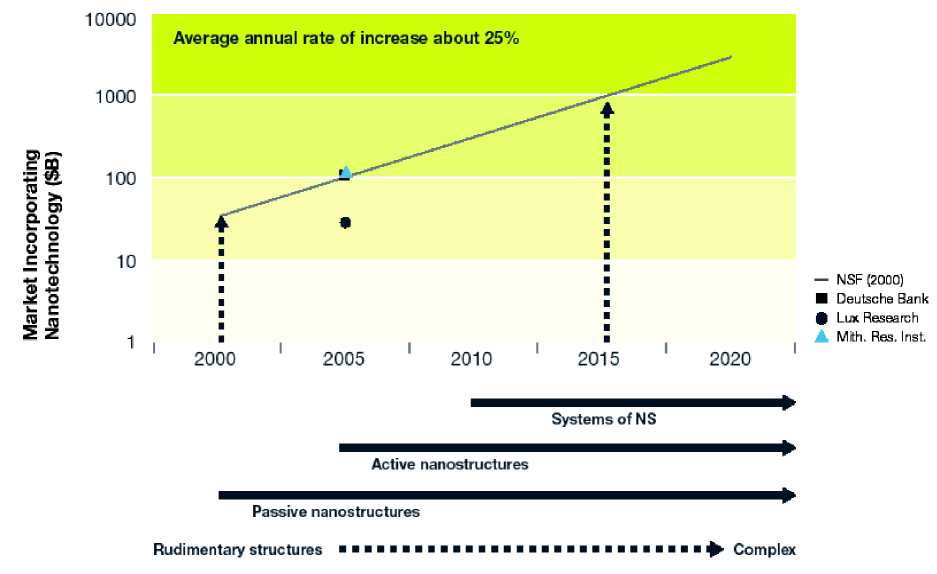
Figure 15. Worldwide Market Affected by Nanotechnology (NSF estimation made in 2000, the estimation holds in 2006)

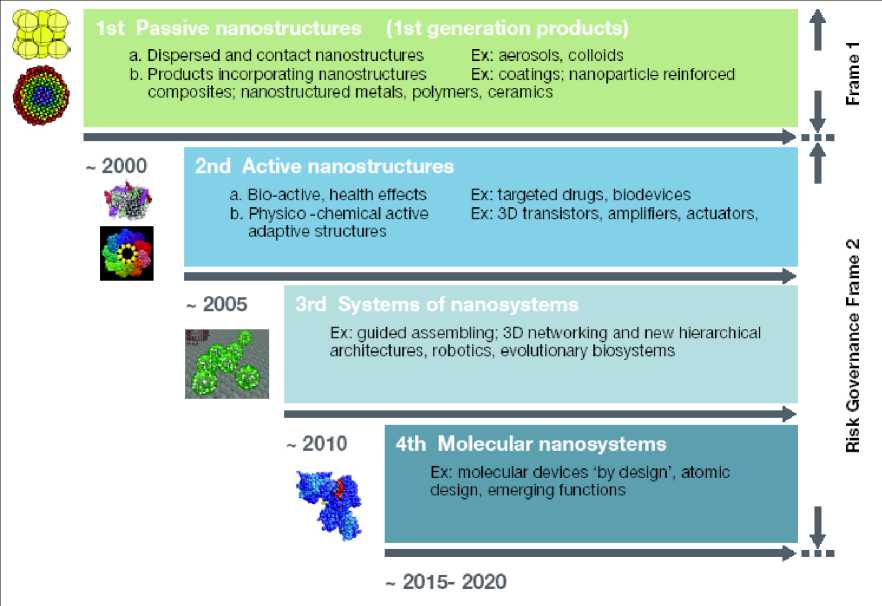
Figure 16. Timeline for Beginning of Industrial Prototyping and Nanotechnology Commercialisation: Four Generations of Products and Production Processes

Recent forecasts by Mitsubishi Research Institute (Japan), Deutsche Bank (Germany), Lux Research (US) and other organisations, mainly based on NSF data, also support the estimated $1 trillion by 2015, even if the 2004 data of Lux Research does not include current nanoscale applications in electronics and catalysts. However, these estimates derive from variable base lines, some of which include entire products (e.g. hard disks) rather than nanotechnology components themselves (e.g. data storage layers).

Significant applications of nanosciences and nanoengineering already exist in the fields of, inter alia, medicine, pharmaceutics, cosmetics (such as sun creams), biotechnology, processed food, chemical engineering, high performance materials, electronics, information technologies, precision mechanics, optics, analytics, energy production and environmental sciences (Jopp, 2003). Currently, nanotechnology products can be found in:

• •    Paints (for example crack-resistant paint using antimony-tin oxide);

• •    Fuel cells;

• •    Batteries;

• •    Fuel additives;

• •    Catalysts;

• •    Components in transistors;

• •    Sources of lasers and lighting;

• •    Lubricants;

• •    Integrated circuitry;

• •    Medical implants;

• •    Machine ceramics;

• •    Water purification and remediation;

• •    Military battle suits;

• •    Self-cleaning windows;

• •    Sunscreens and cosmetics;

• •    Explosives, propellants and pyrotechnics;

• •    Disinfectants;

• •    Abrasives;

• •    Food additives.

Thousands of new patents are being announced in this area each year (Huang et al. 2004). Titanium dioxide, carbon black, zinc oxide and iron oxide make up the majority of the nanoparticles in industry, and there are dozens of other nanostructures and particles at the research stage that could soon enter the manufacturing world as part of the first generation of nanoproducts (see evolution of nanotechnology in Figure 16).

The Small Times survey, using the NNI definition of nanotechnology, has identified over 700 products incorporating nanotechnology in the US alone (Small Times, 2005).

What is Special about Nanotechnology as an Emerging Field?

Nanotechnology has many characteristics which both increase its potential and produce new issues for global risk governance. The implications of nanotechnology are broad because its applications are at the confluence with modern biology, the digital revolution and cognitive sciences (nano-bio-info-cogno, converging technologies or NBIC in Roco and Bainbridge, 2003). The results of NBIC integration are expected to lead to significant long-term impacts.

Most importantly, nanotechnology is unique as it:

• •    Offers a broad technology platform for industry, biomedicine and environment as well as an almost infinite array of potential applications.

• •    Holds promises for applications which have the potential to manage many technical, economic, ecological and social problems.

• •    Allows manipulation at the basic level of organization of atoms and molecules, where the fundamental properties and functions of all manmade and living systems are defined.

• •    Provides opportunities for reversing the trend of specialization of scientific disciplines, unifying concepts in research and education, and for the integration of engineering and technology systems.

• •    Has stimulated all developed countries and many other countries to invest in nanotechnology.

• •    Has broadened and changed manufacturing capabilities (e.g. by self-assembly, templating, stamping and fragmentation, amongst others) with the promise of even more efficient outcomes.

• •    Has become one of the main drivers for technological and economic change and is already stimulating considerable industrial competition.

Reflecting the specific characteristics of nanotechnology, national R&D programmes established during the last five years have become highly integrative, involving multiple funding agencies. For example, the strategy of the NNI is based on: long-term planning;

Four Generations of Nanotechnology Products and Production Process

Four overlapping generations of new nanotechnology products and processes (called below nanoproducts) have been identified with the potential for development in the period 2000-2020: passive nanostructures, active (evolving function) nanostructures, integrated nanosystems, and heterogeneous molecular nanosystems (see, Figure 16; Roco, 2004). Each generation of products is marked by the creation of commercial prototypes using systematic control of the respective phenomena and manufacturing processes. Products may also include components which correspond to different generations. Today’s rudimentary capabilities of nanotechnology for systematic control and manufacture at the nanoscale are expected to evolve significantly in both complexity and the degree of integration by 2020.

• •    First generation of products, mainly after ~ 2000: passive (steady function) nanostructures. For example: nanostructured coatings, dispersion of nanoparticles, surface nanopatterning, ultraprecision engineering, and bulk materials (nanostructured metals, polymers and ceramics). These nanostructured materials are relatively simple with passive or merely reactive behavior, and have steady or quasi-steady structures and functions during their use (such as mechanical behavior and chemical reactivity). The primary products are components (such as particles, wires, nanotubes) with improved properties and functions because of their nanostructure.

One may identify two subcategories:

• ( a) dispersed and contact surface nanostructures such as nanoscale colloids (including cosmetics), aerosols and powders that may have significant exposure to bio-systems; and (b) products incorporating nanostructures such as nanoscale layers in transistors or bulk materials. In nanomedicine, one would include the integration of joint replacement with biocompatible nanostructured materials, and non-invasive and invasive diagnostics with nanoparticles and quantum dots for rapid patient monitoring. In nanoelectronics, one would include the integration of the scaled down masked-lithography of thin-films approach with simple nanoscale components (for example, nanolayers). Potential high-risk products are nanoparticles in cosmetics or food with large scale production and high exposure rates, and ultrafine powders - the latter being potential fire and explosion hazards.

• •    Second generation of products, ~ 2005: active (evolving function) nanostructures. For example: transistors, amplifiers, targeted drugs and chemicals, actuators, molecular machines, light-driven molecular motors, plasmonics (the technology of transmitting light-like waves along nanoscale wires), nanoscale fluidics, laser-emitting devices, and adaptive structures. An active nanostructure changes its state during operation: for example, an actuator changes its dimensions, and a drug delivery particle changes its morphology and chemical composition. The new state may also be subject to successive changes in the mechanical, electronic, magnetic, photonic and biological properties, as well as other effects.

One may identify two subcategories: (a) bio-active nanostructures with potential effects on human health and ecosystems; and (b) physico-chemical active nanostructures. Typical active nanostructures include components in nanoelectromechanical systems (NEMS), nanobiodevices, energy storage devices, actuators, and sensors which change their state during measurement.

In nanomedicine, one would include cognitive capacity-assisting and enhancing devices, targeted cancer therapies, sensors for in vivo monitoring, localised drug delivery, neural stimulation and cardiac therapies. In nanoelectronics, one would include directed self-assembly structures allowing the scaling down of complementary metal-oxide semiconductors (CMOS) to their ultimate limits (5-10 nm) and the possible postCMOS (but still electron charge-based) integrating nanocomponents and nanodevices such as carbon-nanotube and single-electron transistors. Examples of potential high-risk products are: nano-bio interface devices, neuro-prosthetics, reactive devices placed in the environment, active devices in the human body, and devices for surveillance. Potential higher-risk areas are: nano-biotechnology; neuro-electronic interfaces; nanoelectromechanical systems; agriculture and food systems; and hybrid nanomanufacturing.

• •    Third Generation, ~ 2010: integrated nanosystems (systems of nanosystems). For example: the use of various synthesis and assembling techniques such as bio-assembling; networking at the nanoscale and multiscale and hierarchical architectures; robotics on surfaces; modular nanosystems; chemo-mechanical processing of molecular assemblies; evolutionary bio- and hybrid- nanosystems; and quantum-based nanoscale systems. In nanomedicine, one would include artificial organs built from the nanoscale, improved cell-material interactions for cell conditioning, and scaffolds for tissue engineering. In nanoelectronics, one would include new devices based on states other than electric charge (e.g. electron-spin, nuclear-spin or photonic states). Examples of potential high-risk products include: emerging behavior robotics, evolutionary artificial organs, modified viruses and bacteria, and brain modification. Several potential higher-risk areas are: nanorobotics; regenerative medicine; brain-machine interface; nano-engineering in agriculture;

nanosystems used for manufacturing and product processing; and other converging technologies and applications.

• •    Fourth generation, ~ 2015/2020: heterogeneous molecular nanosystems. In this generation each molecule in the nanosystem has a specific structure and plays a different role. Molecules will be used as devices and fundamentally new functions will emerge from their engineered structures and architectures. This is approaching the manner in which biological systems work but, in comparison, biological systems are water-based, process information relatively slowly, and have multiple hierarchical scales. The design of new atomic and molecular assemblies is expected to increase in importance through for example: the creation of macromolecules “by design” to self-assemble on multiple scales; nanoscale machines; subcellular interventions; directed and multiscale self-assembling; controlled interaction between light and matter with relevance to energy conversion; and the exploitation of quantum control. NBIC convergence will play an increased role in this generation. In nanomedicine, one would include nanoscale genetic therapies, cell ageing therapies, and nanoscale controlled stem cell therapies. In nanoelectronics, one can envisage molecular and supramolecular components for transistors. Examples of potential high-risk products are: molecular devices “by design”; molecules with atomic design; large nano-bio or hybrid systems with emerging functions; evolutionary cells; and self-replication of large nanostructured systems. Potential higher-risk areas include: neuromorphic engineering, complex systems, molecular nanosystems used for manufacturing and product processing, and human-machine interface. Thus emerging and integrated characteristics of nanotechnology create a situation whereby the risk perception of one application may create images and drive apprehension of other applications with the label nanotechnology that, in reality, require quite different risk governance strategies (see Table 1).

Table 1. The Different Generations and Frames of Nanotechnology Development

	Four Generations
		<4 • "■ 1 fcSF ё± 1 jo 1 1 <—r| I ^1 [ erll— Lt^ Г 1 s Ll C S	Risk Governance Context
8	First Generation — passive (steady function) nanostructures og. nanostructured coatings and non-invaslve; invasive diagnostics for rapid patient monitoring From 2000 -	Behaviour: Inert or reactive nanostructures which have stable behaviour and quasi -constant properties during their use. Potential risk: e.g. nanoparticles In cosmetics or food with large scale production and high exposure rates.	Current context Tor Frame 1 products and processes; Interested parties are seeking to develop knowledge about the properties of nanomaterials and their EHS Implications so that risks can be characterised Internallonally. Debates are focused on the design and Implementation of best practices and regulatory pol Ides. Risk characterisation: the nanoscale components of the nanoscale products and processes result In Increased system component complexity. Strategies: the establishment of an Internationally reviewed body of evidence related to toxicological and ecotoxlcologlcal experiments, and simulation and monitoring of actual exposure. Potential conflict: the question of how much precaution Is necessary when producing the nanomaterials (focusing on changes to best practices and regulation) and over their use In potential applications.
	Second Generation — active (evolving function nanostructures) e.g. reactive nanostructured materials and sensors: targeted cancer therapies From 2005 -	Behaviour: the nanostructures" properties are designed to change during operation so behaviour Is variable and potentially unstable. Successive changes In state may occur (either Intended or as an unforeseen reaction to the external environment). Potential risk: e.g. nanoblodevlces In the human body: pesticides engineered to react to different conditions.	Current context for Frame 2 products and processes; Interested parties are considering the social desirability of anticipated Innovations. Debates are focused on the process and speed of technical modernisation, changes In the Interface between humans, machines and products, and the ethical boundaries of Intervention Into the environment and living systems (such as possible changes In human development and the Inability to predict transformations to the human environment). Risk characterisation: the nanoscale components and nanosystems of the Frame 2 products and processes
8	Third Generation — Integrated nanosystems (systems of nanosystems) e.g. artificial organs built from the nanoscale; evolutionary nanoblosysterns From 2010 -	Behaviour: passive and/or active nanostructures are Integrated Into systems using nanoscale synthesis and assembling techniques. Emerging behaviour may be observed because of the complexity of systems with many components and types of Interactions. New applications will develop based on the convergence of nanotechnology, biotechnology. Information technology and the cognitive sciences (NBIC). Potential risk: e.g. modified viruses and bacteria; emerging behaviour of large nanoscale systems.	result In knowledge uncertainty and ambiguity. Strategies: stakeholders must achieve understanding, engage In discussion about ethical and social responsibility for Individuals and affected Institutions and build Institutional capacity to address unexpected risks. Projected scenarios need to be explored that show plausible (or Implausible) links between the convergence of technologies and the possible social, ethical, cultural and perception threats. A major challenge Is that decisions need to be undertaken before most of the processes and products are known. Potential conflicts: the primary concern of Frame 2 Is that the societal Implications of any unexpected (or expected but unprepared for) consequences and the Inequitable distribution of benefits may create tensions
	Fourth Generation — heterogeneous	Behaviour: engineered nanosystems and architectures are created from Individual	If not properly addressed. These concerns about technological development may not be exclusively
	molecular nanosystems e.g. nanoscale genetic therapies; molecules designed to	molecules or supramolecular components each of which have a specific structure and are designed to play a particular role. Fundamentally new functions and processes begin to emerge with the	associated with It and will Impact upon stakeholder perceptions and concerns.
	sei fassemble From 2015/2020 -	on that of biological systems. Potential risk: e.g. changes In biosystems; Intrusive Information systems.

Table 1 provides an overview of the risk governance context for both Frame 1 and Frame 2.

For that reason it is proposed that nanotechnology development is not viewed as a single consolidated concept but, rather, is categorized into four overlapping generations of new nanotechnology products and processes, each generation having its own unique characteristics: passive nanostructures, active nanostructures, complex nanosystems, and molecular nanosystems (see Table 1). Furthermore, a second distinction can be made in terms of risk perception between the first generation (referred to in Table 1 as Frame 1) and the following three generations (Frame 2) as the extent of knowledge development and the ability to control nanostructure behavior is more advanced for Frame 1 and the potential social and ethical consequences are expected to be more transformative for Frame 2. Structuring nanotechnology risk governance into these two broad frames of reference allows for research and decision-making pathways to be adapted to the characteristics of each frame and, equally, for risks and concerns to be identified separately.

In present manuscript we are concentrate our attention on the description of efficient quantum feedback control models, its physical limits and information bounds and tradeoffs between performance, stability and robustness. We are considered separating the problem of designing Hamiltonian quantum feedback control algorithm into a measurement (estimation) strategy and a feedback (control) strategy, and we consider optimizing desirable properties of each under the minimal constraint that the available strength of both is limited. These motivate concepts of information extraction and disturbance that are distinct from those usually considered in quantum information theory.

Using these concepts we identify an information trade-off in quantum feedback control. Software/Hardware implementations of the developed simulation system of quantum control algorithm benchmarks are described.

Conclusions

Recently, the interest to the control of quantum systems started to grow rapidly. According to the Science Citation Index, by the beginning of this century more than 500 papers were published annually in the cited journals. The reader can judge the state-of-the-art in this area by the papers published in the collected translations and collected articles cited in References. Studies on the quantum computers represent one of the important applications.

As conclusion to our preface about current knowledge in quantum optimal control theory we can introduce for our reader very old instructive history as following: An Indian and a white man fell to talking. The white man drew a circle in the sand and a larger circle to surround it. “See”, he said, pointing to the small circle “that is what the Indian knows, and that”, pointing to the larger circle, “is what the white man knows.” The Indian was silent for many minutes, and then slowly he pointed with his arm to the east and turned and waved to the west. “And that, white man”, he said “is what neither of us knows”.