Модернизация системы регистрации масс-спектрометров МИ1201 с непрерывной разверткой

В ряде промышленных отраслей в настоящее время применяются масс-спектрометры МИ1201 с непрерывной разверткой, которые используются в технологическом цикле для контроля продукта в газовой и твердой фазе. Большинство таких масс-спектрометров имеют в своем составе морально и физически устаревшие системы регистрации. Основными целями настоящей работы являлось повышение точности, надежности и производительности измерений за счет введения измерительных и вычислительных устройств нового поколения, совершенствования алгоритмов измерения и обработки данных, внедрения новых компьютерных технологий по представлению и хранению данных.

ЭЛЕКТРОМЕТРИЧЕСКИЙ УСИЛИТЕЛЬ

В большинстве масс-спектрометров МИ1201 с непрерывной разверткой, применяемых в технологических процессах по анализу изотопного состава продукта, до настоящего времени используются ламповые электрометрические усилители. Такие усилители морально и физически устарели. Для снижения шумов, повышения чувствительности и надежности были разработаны электрометрические усилители на интегральных микросхемах. В работе [1], выполненной с участием авторов, была рассмотрена принципиальная схема и приведены технические характеристики электрометрического усилителя на основе гибридной интегральной микросхемы МРТИ 3.456.001. Такая микросхема была разработана и серийно выпускалась Минским приборостроительным объединением. Усилители на базе этой гибридной микросхемы использовались в ряде модернизированных масс-спектрометров МИ1201 и в новом отечественном изотопном технологическом масс-спектрометре МТИ350Г, предназначенном для анализа гексафторида урана [2, 3]. Следующим шагом по совершенствованию электрометрической аппаратуры является замена в усилителях гибридных микросхем на интегральные. Такая замена позволяет повысить надежность и технологичность сборки в условиях серийного и мелкосерийного производств масс-спектрометров.

В качестве интегральной микросхемы первого каскада усилителя была выбрана микросхема LPC661M фирмы National Semiconductor.

Электрометрический усилитель построен по двухкаскадной схеме с обратной связью по току. Структурная схема усилителя приведена на рис. 1.

Входной каскад питается пониженными напряжениями (+7 В, –7 В) и работает в режиме малых выходных сигналов, что обеспечивает минимально достижимые для примененного типа электрометрических микросхем шумы и дрейф усилителя, а также исключение влияния уровня преобразуемых токов на выходной сигнал.

Конструктивно электрометрический усилитель представляет собой печатную плату с габаритными размерами 60 × 30 мм, которую можно установить в корпус электрометрических усилителей многоколлекторного или одноколлекторного приемника ионов. Входной контакт и элементы входной цепи усилителя установлены на изоляторы из лейкосапфира, обладающего минимальными ко-

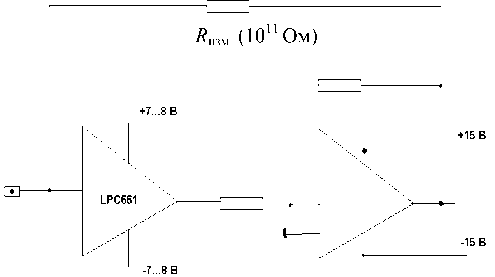
Рис. 1. Структурная схема электрометрического усилителя

Рис. 2. Cпад интенсивности ионного тока изотопа 4. R ос = 470 ГОм (сопротивление в цепи обратной связи).

По оси абсцисс — время × 0.2 с. По оси ординат — интенсивность в мВ

эффициентом абсорбции и током утечек. Для проведения испытаний усилитель устанавливался в технологический корпус с типовым электрометрическим вводом.

Испытания макета усилителя проводились при измерительном резисторе Rизм= 1011 Ом, длительность единичного измерения составляла около 2 с. При проведении испытаний электрометрический усилитель подключался к технологическому стенду. Диапазон выходных напряжений определялся по показаниям вольтметра Щ1518, подключенного к выходу стенда при изменении входного тока усилителя с помощью регулятора и переключателя полярности технологического стенда.

Среднеквадратичное значение шума усилителя определялось по формуле

U

∑ ( U - U i )²

N - 1

где U — среднее значение выходного напряжения усилителя; U i — единичное измерение выходного напряжения усилителя, произведенное вольтметром за время 2 с; N — количество измерений ( N = = 10).

Определение дрейфа нулевого уровня электрометрического усилителя проводилoсь следующим образом: измеряли среднее значение выходного напряжения при нулевом входном токе, а уровень дрейфа определялся по изменению среднего значения выходного напряжения в течение часа.

Определение среднеквадратичного значения сигнала проводилoсь при установке регулятором технологического стенда выходного сигнала в пределах от 2 до 4 В.

В результате измерений получены следующие данные: U ш изменялся от 35 до 40 мкВ. Дрейф нулевого уровня — 27 мкВ/ч. Среднеквадратичное значение сигнала 70 мкВ.

Таким образом:

• •    динамический диапазон измерений — 2.5 × 10⁵ (от 40 мкВ до 10 В),

• •    дрейф нулевого уровня — < 50 мкВ/ч,

• •    среднеквадратичное значение шума — < 50 мкВ при времени интегрирования 2 с,

• •    среднеквадратичное значение шума сигнала технологического стенда при времени интегрирования 2 с — < 100 мкВ,

• •    смещение нуля регулируется в пределах от 0 до 5 мВ.

Параметры операционного КМОП-усилителя LPC661:

• •    ток потребления — 55 мк,

• •    коэффициент усиления — 120 дБ,

• •    дрейф — 1.3 мкВ/ 1 °С,

• •    минимальный входной ток — 2∙10^–15 А,

• •    полоса пропускания — 1 кГц,

• •    напряжение питания — 5…15 В.

Проведенные испытания усилителя в статическом режиме при измерениях ионных токов в диапазоне от 10–15 до 10–10 А подтвердили его технические характеристики, которые приведены выше и были получены на технологическом стенде. В динамическом режиме при переходе с вершины пика испытания показали, что постоянная времени усилителя не превосходит постоянной времени цепи управления магнитным полем. На рис. 2 показан сигнал с выхода усилителя по- сле переключения магнитного поля с вершины пика. Основными преимуществами рассмотренной схемы являются:

• •    возможность установки пониженного напряжения питания на микросхеме первого каскада, что снижает нагрев микросхемы при измерении интенсивных пиков;

• •    улучшенные динамические характеристики за счет построения двухкаскадной схемы;

• •    технологичность сборки усилителя за счет использования интегральной, а не гибридной микросхемы.

АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ И ФИЛЬТР НИЖНИХ ЧАСТОТ

Для измерения выходных сигналов электрометрических усилителей в модернизированной системе регистрации используется прецизионная плата аналого-цифрового преобразования ЛА-И24 [4], которая серийно выпускается в Центре АЦП ЗАО "Руднев—Шиляев". В состав платы входят микросхема аналого-цифрового преобразователя AD7710 фирмы Analog Device, который построен на основе принципа "сигма—дельта", и инструментальный усилитель с программируемым коэффициентом усиления. Преимуществами АЦП, построенных по принципу "сигма—дельта", для прецизионного измерения сигналов изотопных масс-спектрометров является большое количество разрядов (в данном случае 24) при меньшем времени преобразования по сравнению с АЦП, построенными по другим принципам, например преобразователями напряжения в частоту и АЦП интегрирующего типа. Кроме того, в АЦП, построенных по принципу "сигма—дельта", автоматически производится цифровая фильтрация сигналов. В дополнение к цифровой фильтрации, производимой непосредственно в микросхеме АЦП, на плате ЛА-И24 установлен цифровой фильтр нижних частот с программируемой частотой среза.

Благодаря цифровой фильтрации в обработку поступают только те сигналы, максимальная частота которых не превышает половины частоты дискретизации (выборки) сигнала. Частота дискретизации (выборки) сигналов устанавливается программно. В масс-спектрометре для изотопного анализа с непрерывной разверткой правильная установка частоты дискретизации (выборки) является принципиально важной задачей. При низкой частоте выборки после цифровой фильтрации можно получить высокое отношение сигнал/шум, но ошибочно производить оценку максимумов масс-спектральных пиков, т. к. максимальное значение пика может оказаться в промежутке между точками дискретизации сигнала. При высокой частоте дискретизации мы "не пропустим" вершину пика, но получим сигнал с низким отношением сигнал/шум.

Например, при частоте дискретизации (выборки) 11.45 Гц среднее квадратичное значение шума (при отсутствии сигнала) равно 0.24 мВ, а при частоте дискретизации 21.51 Гц — 0.46 мВ.

При повышении частоты дискретизации в сигнале, который поступает в компьютер для дальнейшей обработки, повышается среднее квадратичное отношение шума и появляется синусоидальный сигнал наводки. Фильтр нижних частот, который находится на плате АЦП, не пропускает сигнал наводки и снижает среднее квадратичное значение шума.

АЛГОРИТМЫ ОБРАБОТКИ МАСС-СПЕКТРОВ

В дополнение к алгоритмам обработки спектров, рассмотренных в статье [4], в данной работе рассматриваются алгоритмы сглаживания, обнаружения спектральных линий, коррекции влияния фона рассеянных ионов и "восстановления" ошибочно отбракованных измерений амплитуд спектральных линий.

Сглаживание измеренных масс-спектров

Для повышения отношения сигнал/шум кроме цифровой фильтрации в плате АЦП целесообразным также является применение сглаживания экспериментальных данных. Для сглаживания изотопных масс-спектров, полученных при непрерывной развертке, необходимо выбрать такой алгоритм, который позволил бы с одной стороны максимально возможно повысить отношение сиг-нал/шум, а с другой стороны минимально исказил форму масс-спектрометрического сигнала, в том числе форму вершины масс-спектрометрического пика. Наиболее простым, но в то же время хорошо удовлетворяющим поставленной задаче является сглаживание "скользящим" квадратичным полиномом [5]. Квадратичный полином строится с помощью весовых коэффициентов. Сглаживание производится "скользящим" окном из пяти точек. Значение полученной функции Y i после сглаживания в центре окна вычисляется по формуле:

Y i = w –2 Y i – 2 + w –1 Y i – 1 +

+ w 0 Y i + w 1 Y i +1 + w 2 Y i +2 , (2)

где Y i –2 , Y i –1 , Y i +1 , Y i +2 — соседние слева и справа от Y i экспериментальные данные, а значения весов w –2 , w –1 , w 0 , w 1 , w 2 соответственно равны 0.0625, 0.250, 0.375, 0.250, 0.0625.

На рис. 3, 4 представлены первичные экспериментальные данные на вершине масс-спек-трального пика и данные, полученные после сглаживания рассмотренным методом и методом Савицкого—Галлея [6], который является наиболее

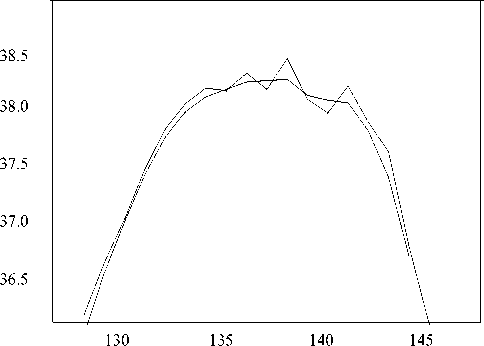
Рис. 3. Вершина пика после сглаживания квадратичным полиномом на основе весовых коэффициентов (ломаной линией показаны экспериментальные данные)

сглаживания с весовыми коэффициентами гораздо роще в реализации.

Обнаружение спектральных линий в изотопном масс-спектре

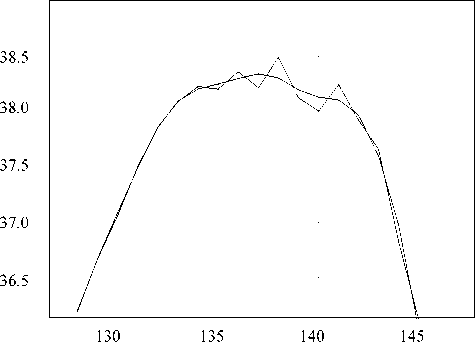
Рис. 4. Вершина того же пика, что на рис. 3, после сглаживания методом Савицкого—Галлея при длине окна, соответствующего 1.5 % от длины массива обрабатываемых данных

При обнаружении спектральных линий в изо-опном масс-спектре достаточным является обна-ужение двух самых интенсивных линий спектра, параметры остальных можно определить по рас-читанному их положению на шкале массовых чи-л. Обнаружение интенсивных линий может быть существлено по алгоритму сравнения с порогом змеренных значений ионных токов [4, 7]. Обычно лгоритм сравнения с порогом плохо работает при бнаружении спектральной линии при отношении сигнал/шум меньше пяти. Как показал опыт работы, в ряде задач по измерению изотопного состава продукта с помощью указанного алгоритма может быть устойчиво обнаружен только один спектральный пик в том случае, когда интенсивность второго пика не превышает среднего квадратичного отклонения шума более чем в пять раз. Более устойчивыми алгоритмами обнаружения при соотношении сигнал/шум меньше пяти являются алгоритмы, основанные на вычислении взаимо-корреляционных функций выборочных значений ходного сигнала I_i c известным нормированным о амплитуде описанием формы полезного сигна-а [10]. Аналогичными по возможностям обнару-ения являются алгоритмы, основанные на вы-ислениях функции свертки (конволюции) выбо-очных значений исходного сигнала, так же как и предыдущем случае, с нормированным по ам-литуде описанием формы полезного сигнала.

Математическое описание формы полезного игнала в масс-спектрометрах МИ1201 может ыть осуществлено по алгоритму, описанному работах, выполненных с участием авторов даной статьи [8, 9].

Качественно форму пика можно вывести до опыта из теоретических соображений. Поскольку обычно форма одиночного пика масс-спектрометра качественно близка к гауссовой кривой, можно в качестве модели одиночного спектрального пика использовать композицию функции Гаусса

( s (t) = exp

V

. I

/

распространенным в сглаживании экспериментальных спектров.

Сравнение двух рассмотренных методов сглаживания показало, что оба метода уменьшают среднеквадратичное значение шума приблизительно в два раза. При сглаживании на вершине пика, как показано на рис. 3, 4, оба метода практически не искажают форму пика, однако метод

и прямоугольной функции

rect ( t ) =

1, 0,

1 1 <  t <  1 2 , t <  1 1 или

t >  1 2 ,

которая описывает влияние широкой щели. Такая композиция представляет собой примерно равномерную полосу в своей средней части и быстро

спадающую по краям и выражается образом:

следующим

i ( t ) = A •

V V

(

Ф

(

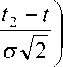
+ Ф

V

t - t 1

a 2 1 JJ

….(3)

где Ф — функция Лапласа, a — полуширина пика, А — масштабный множитель.

В представленной модели пика расстояние между точками t 1 и t 2 ( t 2 – t 1 ) характеризует величину выходной щели масс-анализатора. В многочисленных масс-спектрометрических экспериментах с непрерывной разверткой широкая щель приводит к значительному снижению разрешающей способности и не позволяет точно оценивать амплитуды малых пиков, находящихся на расстоянии в 1 а.е.м. от пиков с большей амплитудой. В этом случае модель формы пика, представленной выражением (3), следует уточнить. При масс-спектрометрических экспериментах, в которых достаточно узкая щель в масс-анализаторе, форма пика может быть описана либо гауссовой функцией (4), или с помощью выражения (5):

si = exp(-( t - a )²/ (2 o ²)),           (4)

s2 = A-(Ф(( а / 2 + 8 - 1 ) / a ) +

+ Ф(( t - ( a / 2 - 8))/ ( a ))).        (5)

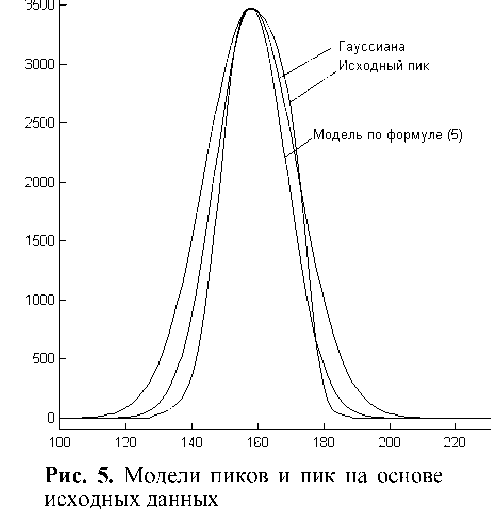
На рис. 5 представлен пик, построенный на основе экспериментальных данных, и пики, построенные на основе моделей по формулам (4) и (5).

Для выбора алгоритма обнаружения было проведено исследование возможностей нескольких вариантов алгоритмов, в которых форма пика описывалась различными функциями. Критерием выбора являлось минимальное отношение сиг-нал/шум при минимальной ошибке оценки параметров пиков.

В основе алгоритма обнаружения лежит метод вычисления свертки (конволюции) исходных данных в "скользящем окне" с функцией, описывающей форму пика. Алгоритм представлен в виде выражений (6), (7), (8), (9):

A1(i) = conv(s_ish(i), s1),(6)

A2(i) = conv(s_ish(i), s2),(7)

A3(i) = conv(s_ish(i), s_treug),(8)

A4(i) = conv(s_ish(i), s_trapecija),(9)

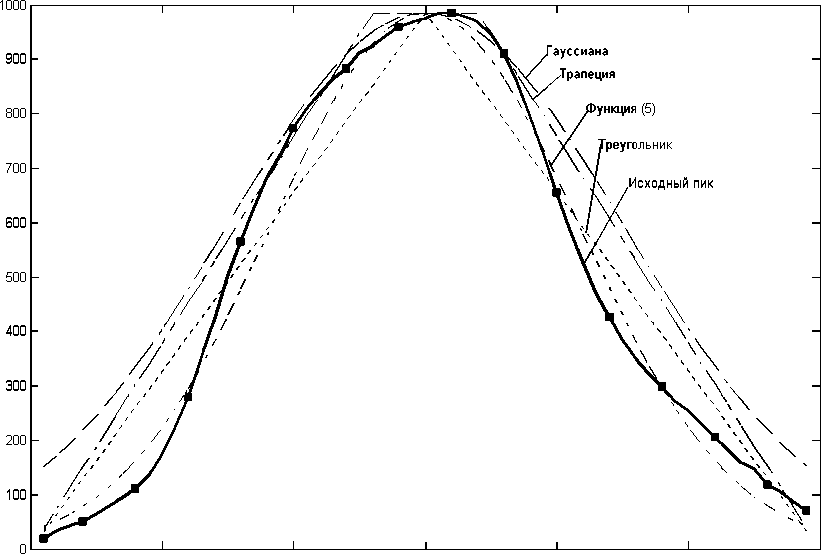
где s_ish — исходные данные экспериментального спектра; s1 — форма пика, описанная функцией Гаусса (выражение (4)); s2 — форма пика, описанная выражением (5); s_treug — форма пика, представляющая треугольник, вписанный в исходные данные; s_trapecija — форма пика, представляющая трапецию, в которую вписаны исходные данные; сonv — оператор, вычисляющий функцию свертки (конволюции). На рис. 6 представлены графики функций, описывающих форму пика, и пик, построенный на основе экспериментальных данных. Ширина окна исходных данных, в котором вычисляется функция свертки, равняется ширине пиков, которые обнаруживаются.

В результате вычисления операции свертки получается совокупность чисел, которая повторяет измеренный спектр с амплитудами пиков, более чем в 10 раз превышающими исходные, но полученный спектр гораздо более гладкий. Получается как бы усиление одновременно со сглаживанием. После этого обнаружить пики в такой совокупности чисел очень легко по пороговому алгоритму.

В таблице приведены результаты исследований возможностей обнаружения пиков алгоритмами, представленными выражениями (6), (7), (8), (9). Исследования проводились методом математического эксперимента. К спектру, полученному из экспериментальных данных, добавлялись различные реализации случайных чисел, плотность распределения которых соответствовала нормальному закону. Наименьший пик в спектре считается обнаруженным, если локальный максимум функции, построенный на основе сверток, появляется на заданном участке спектра. При этом не должно быть обнаружено дополнительных пиков. Правильное обнаружение отмечено в таблице знаком "+". Отношение сигнал/шум в столбцах таблицы помечено символами S/N.

О                  10                  20                  30                  40                  50                  60

Рис. 6. Исходный пик и функции, описывающие форму пика

Результаты экспериментов по обнаружению масс-спектрометрических пиков алгоритмами (6)–(9)

№ опыта	Алгоритм (6)		Алгоритм (7)		Алгоритм (8)		Алгоритм (9)
	S/N	Пики обнаружены	S/N	Пики обнаружены	S/N	Пики обнаружены	S/N	Пики обнаружены
1	1.43	+	0.95	—	0.99	—	0.95	+
2	0.86	+	1.50	+	1.86	+	0.85	+
3	0.77	—	1.01	+	1.86	+	0.64	+
4	0.87	—	1.52	+	1.14	+	0.81	—
5	1.11	+	1.72	+	1.10	+	1.33	+
6	1.47	+	1.19	+	1.04	+	0.79	+
7	0.80	+	0.97	+	0.91	—	0.69	—
8	1.05	+	1.52	+	0.80	+	0.84	—
9	1.10	+	1.65	+	0.67	—	1.08	+
10	1.38	+	1.54	+	1.26	+	0.96	+
11	1.66	+	0.87	—	1.42	+	0.99	+
12	1.07	+	0.92	+	0.64	—	1.03	+

Анализ результатов, приведенных в таблице, показывает, что все четыре алгоритма имеют одинаковые возможности по достоверному обнаружению пиков при отношении сигнал/шум 1.0 и выше. Данные исследования дали возможность реализовать в рабочей программе самый простейший из четырех рассмотренных алгоритмов. Таким алгоритмом является алгоритм (8) — вычисления свертки с формой пика в виде треугольника.

Компенсация влияния фона рассеянных ионов

Погрешность оценки амплитуд пиков в изотопном масс-спектре зависит от правильной компенсации фона рассеянных ионов. Фон рассеянных ионов возникает по двум причинам:

• 1)    взаимодействие ионов исследуемого вещества с молекулами и ионами остаточного газа в масс-анализаторе при недостаточной откачке;

• 2)    соударение ионов исследуемого вещества со стенками камеры масс-анализатора.

Фон рассеянных ионов приводит к тому, что малые пики, находящиеся вблизи значительно более интенсивных пиков, находятся на "хвостах" этих пиков. Для точной оценки малых пиков необходима точная аппроксимация формы "хвоста" больших пиков. Выше было отмечено, что форму линий изотопного масс-спектра в приборе с узкой щелью можно аппроксимировать функциями, представленными выражениями (4) и (5). На рис. 7 представлен участок масс-спектра, на котором малый пик целиком сидит на "хвосте" большого. При этом наименьшее значение ("провал") перед малым пиком (слева) больше, чем наименьшее значение после пика. Для компенсации влияния фона рассеянных ионов можно использовать указанные выше модели пика или использовать линейную функцию, которая соединяет наименьшие значении слева и справа от малого пика. На рис. 7 показана такая линейная функция. Как показала практика, основанная на измерениях стандартов, т. е. проб с известным изотопным составом, наиболее точные результаты дает алгоритм, вычисляющий среднее из величин, взятых из указанной выше прямой в момент времени, соответствующий центру пика, и из функции, описывающей форму пика, для того же интервала времени. Для компенсации влияния фона рассеянных ионов в качестве функции, описывающей форму пика, может быть принята гауссиана или функция (5). На рис. 7 стрелкой показан отрезок прямой, верхняя часть которого является основанием для вычисления амплитуды пика с учетом влияния фона рассеянных ионов.

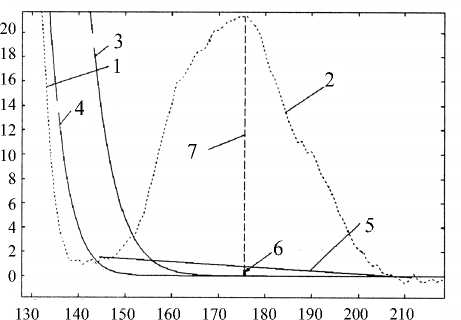
Рис. 7. Компенсация влияния фона рассеянных ионов. 1 — спад большого пика исходных данных, 2 — малый пик исходных данных, 3 — гауссиана, 4 — функция (5), 5 — линейная компенсация вклада рассеянных ионов, 6 — основание для вычисления амплитуды пика, 7 — амплитуда пика с поправкой на фон рассеянных ионов

Восстановление ошибочно отбракованных оценок амплитуд пиков

В отраслевом стандарте Министерства атомной промышленности описан алгоритм, с помощью которого производится отбраковка оценок амплитуд пиков при масс-спектрометрическом анализе изотопного состава продукта. Суть алгоритма в следующем. Пусть имеются оценки амплитуд пиков одного и того же изотопа, измеренные в соседних развертках A1, A2, A3. В соответствии с алгоритмом стандарта вычисляется критерий K5:

K5 = 2×A2/(A1 + A3) – 1. (10)

Если K5 > 0.05, то A2 бракуется и в дальнейших расчетах не участвует. Этот алгоритм хорошо работает, когда К5 не более 0.15, т.е. А2 не является резко выпадающим значением.

Если одно из значений является резко выпадающим, то происходит ошибочная отбраковка других значений. На рис. 8 показан пример, когда при резко выпадающем значении А3 ошибочно бракуется А2. Для восстановления ошибочно отбракованных значений предлагается следующий алгоритм.

• 1)    По значениям амплитуд пиков одного изотопа методом наименьших квадратов находятся коэффициенты прямой, описывающей спад или рост ионного тока в течение опыта, — линейной функции F . Причем в нахождении коэффициентов

  

  Рис. 8. Восстановление ошибочно отбракованных амплитуд. Пояснения в тексте

  
  

такой функции отбракованные значения амплитуд не участвуют.

• 2)    Вычисляется Sk — среднее квадратичное отклонение от функции F .

• 3)    Для всех значений измеренных амплитуд производится вычисление величины R — отклонения амплитуды ионного тока от функции F .

• 4)    Если R >  k × Sk ( k = 2), оценка амплитуды, для которой была вычислена R , остается отбракованной, если нет, то такая оценка амплитуды восстанавливается и участвует в дальнейших расчетах.

После работы указанного алгоритма А2 восстанавливается, а А3 остается отбракованным.

ЗАКЛЮЧЕНИЕ

Описанные выше аппаратные и алгоритмические элементы вошли в состав масс-спектрометрического измерительно-вычислительного комплекса, который прошел испытания в производственных условиях для масс-спектрометрического определения изотопного состава продукции. Получаемая воспроизводимость оценки массовых долей изотопов металлов составила:

не более 0.02 % для массовых долей изотопов с величиной 80% и 0.01 % для массовых долей, меньших 2 %.