Модифицированная арбитражная процедура по последнему предложению с комитетом

Теоретико-игровые модели переговоров активно используются в экономике (задача «продавец – покупатель»), юриспруденции (задача «истец – ответчик»), страховых моделях и др. Если для организации переговоров помимо участников привлекается еще одна независимая сторона – арбитр или несколько арбитров, то такие схемы называются арбитражными процедурами. В настоящее время они актуальны в связи с возникновением в глобальной сети Интернет виртуальных предприятий, в которых для решения различных практических вопросов могут использоваться многоагентные системы. Агенты могут решать как задачи распределения некоторого ресурса, так и проведения конкурсов, составления расписаний, очередности решения задач и др.

Существуют различные модели арбитражных процедур. Наиболее популярна арбитражная процедура по последнему предложению (FOA) [2], [4], [5], [6]. Кроме нее используется схема согласительного арбитража [5], арбитражные процедуры с наказанием [3] и различные комбинированные процедуры [1], [7], [8]. Заметим, что решение в арбитражных процедурах сильно зависит от вида распределения решения арбитра. Большинство работ в этой области касаются моделей с непрерывным распределением решения арбитра. В этом случае равновесие лежит среди чистых стратегий. В работах [1], [7] для дискретного распределения, сосредоточенного в нечетном числе точек, было показано, что равновесие достигается в смешанных стратегиях. При этом не накладывалось никаких ограничений на множество предложений игроков. В работе [8] было найдено равновесие в арбитражной процедуре, где стратегии игроков выбирались из заданных множеств X и Y. В работе [9]

были исследованы арбитражные процедуры, в которых решение принималось не одним арбитром, а арбитражным комитетом. В данной работе мы исследуем арбитражную игру, в которой решение осуществляется комитетом, состоящим из нескольких членов. Используется арбитражная процедура по последнему предложению, точнее, ее модификация. Решение каждого из арбитров моделируется независимыми случайными величинами с одинаковым распределением. Мы будем искать равновесие в таких арбитражных играх в терминах задачи о зарплате, однако этот подход может быть применен и для других задач распределения ресурсов с участием арбитра.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается игра с нулевой суммой, в которой игроки I и II, именуемые соответственно как работник и работодатель, ведут переговоры об установлении заработной платы. Игрок I делает предложение x, а игрок II – предложение y. Мы будем предполагать, что x и y выбираются из заданных множеств X и Y на числовой оси. Если x < у, то конфликта нет и игроки соглашаются на выплату жалованья, равного x + у

.

Если же x >  у , стороны апеллируют к арбитражному комитету.

Арбитражный комитет состоит из нескольких членов. Для простоты предположим, что их число нечетно и равно 2n+1. Каждый из арбитров называет свое решение, а затем сравнивает его с предложениями игроков. В соответствии с арбитражной процедурой по последнему предложению будем считать, что член комитета голосует за того игрока, предложение которого ока- залось ближе к его мнению. Решение принимается в соответствии с правилом большинства. Другими словами, в качестве решения принимается то предложение игрока, за которое проголосовали n+1 арбитров.

Предположим, что решения арбитров представлены независимыми случайными величинами a 1 ,a 2 ,...,a 2 n _{+ 1} с непрерывными функциями распределения F 1 ( a ), F 2 ( a ),..., F 2n _{+ 1}( a ). Тогда, если x >  y , при процедуре арбитража по последнему предложению комитет выбирает предложение y , если решения по крайней мере n + 1 арбитров

, x + У • • • • , 1 a 2 ’ ' = ‘1’'2’"”'* ’ k " n + 1’ в противном случае комитет выбирает x.

Равновесие в процедуре с комитетом было найдено в [8] для случая, когда все распределения F_i ( a ) имеют одинаковую медиану.

Мы исследуем модифицированную процедуру с арбитражным комитетом. Согласно данной процедуре для арбитров, мнения которых попали в интервал предложений [x, y], действуют правила арбитража по последнему предложению (FOA). Если же выбор члена комитета лежит вне данного промежутка, то в качестве решения полагаем x + y .

Вначале мы исследуем модель с одним игроком, с тремя игроками, а затем рассмотрим общий случай.

МОДЕЛЬ С ОДНИМ АРБИТРОМ

Рассмотрим модифицированную арбитражную процедуру с одним арбитром. Следуя правилам процедуры, если решение арбитра принадлежит интервалу

x + У A [y’”J ’

то результатом процедуры будет y. Если же решение принадлежит интервалу x + y то x. В остальных случаях в качестве решения принимается полусумма предложений x + y

.

Тогда функция в игре принимает вид

H ( x , y ) = y I F I x ^ I - F (y ) I +

5 H = x ^- y f f ( x ) - f f x ⁺ y )) + F m ■ F i v ) - F f x + y ) + 1 = 0

a x 2 V' ^J ( 2 ))       2          ( 2 J 2

i

5 H = x ^y f f ( x ) - f f x + y )) + ^{F ( x} ) ^{+ F ( y} ) + f f x + y ) + 1 = о a y 2 I I 2 JJ 2 I 2 J 2

можно найти равновесие.

Пример 1. Если a имеет стандартное нормальное распределение, то из симметрии задачи следует x = -y и система уравнений пре- вращается в условие

- п x 1 - e 2 =. —.

I I 22

Отсюда находим точки y * =- 1.667, x * = 1.667. Нетрудно проверить, что это равновесие в данной процедуре. Заметим, что в обычной FOA процедуре равновесием является

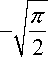
= - 1.253, x * = ^2^ « 1.253.

Таким образом, модифицированная процедура рекомендует игрокам делать большие предложения, чем ранее.

МОДЕЛЬ С ТРЕМЯ АРБИТРАМИ

Рассмотрим арбитражную процедуру с комитетом, состоящим из трех членов. Пусть x <  y . Обозначим интервалы

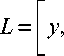
^{x +} y A r "У J ’ R

x + y

и

f x + y ) Z X u = FI -y J - F (y) ’

z x    f x + y )

v = F ( x ) - F  — .

I 2 J

Тогда решение комитета будет y , если решения всех трех арбитров попали в интервал L , вероятность этого u ³ . Или если решения двух из трех попали в L , а третьего нет, вероятность этого C ₃ ² u ² ( 1 - u ) . Или решение одного из трех лежит в L , а двух других не попал₂ и ни в L, ни в R , вероятность этого C ₃ 1 и ( 1 - u - v ) .

Итак, вероятность y есть p1 = и3 + 3и2 (1 - и) + 3и (1 - и - v)2.

Аналогично решение комитета будет x с вероятностью p2 = v3 + 3v2(1 - v) + 3v(1 - и - v)2.

В остальных случаях примем решение равным

(        f x + y )) x + y

+ x F (x) - F    + -

( A 2 JJ 2

( f ( y ) + 1 - F ( x ) ) .

Из системы x + y

.

Это произойдет с вероятностью ( 1 - p 1 - p ₂ ) .

Итак, функция выигрыша равна

\ x + Ун \ x + У

^H ( x , У ) = УРх + xP 2 + у ( 1 - P 1 - P 2 ) = у +

+ x 2 y ( v ³ - u ³ + 3 [ v ² ( 1 - v ) - u ² ( 1 - u ) ] + 3 ( v - u ) ( 1 - u - v ) 2 ) ^.

Равновесие может быть найдено из условий dH (x, y) dH (x, y) ( ’ ) = 0,        ( ’ ) = 0 .

d x                d y

Для функции распределения симметричной формы относительно точки 0 в равновесии должно выполняться условие x = - y и u ( x , y ) = v ( x , y ). Нетрудно показать, что оптимальное решение x удовлетворяет уравнению

2 + x(6v2 -6v + 3)(f(x)-f(0)) = 0,

где v ( x ) = F ( x ) - F ( 0 ) , f ( x ) = F ¹ ( x ) .

Пример 2. Пусть F(x) – функция стандартного нормального распределения. Тогда из уравнения находим x * = 1.352. Отсюда равновесие здесь имеет вид y * »- 1.352, x * » 1.352.

МОДЕЛЬ С 2n+1 АРБИТРОМ

Теперь представим, что комитет состоит из 2n+1 арбитра. Тогда окончательное решение комитета будет y в следующих случаях:

• •    если решения всех 2n+1 арбитров попали в интервал L , вероятность этого u ² n ^{+ 1};

• •    если 2п решений попали в L , а одно нет, вероятность этого C 2 n _{+ 1} u ² n ( 1 - u ) ;

• •    если 2n - 1 решений попали в L , а два других не попали в L , вероятность этого C 2 „n +^- 1 u ² n - 1 ( 1 - u ) ;

• •    и так далее...

•

• •    если n+1 попали в L , а другие n не попали в L , вероятность этого C 2^ + 1 u n ^{+ 1} ( 1 - u ) n .

Кроме того, решение будет y в следующих случаях:

• •    если решения n арбитров попали в L (вероятность этого события равна C n _{n + 1} u n ), из других n+1 ровно j попали в R , а оставшиеся n+1 – j не попали ни в L, ни в R , где j = 0,..., n – 1 . Вероятность этого события равна

( 1 - u - v ) n ^{+ 1} + C n _{+ 1} v ( 1 - u - v ) n + ... + C n + ]¹ v n ^{- 1} ( 1 - u - v ) 2 ;

• •    если n - 1 решений попали в L (вероятность этого события равна C nn ! u n ^{- 1}), из других n+2 решений ровно j попали в R , а оставшиеся n+2 – j не попали ни в L , ни в R , где j = 0,..., n – 2 . Вероятность этого события равна

( 1 - u - v ) + C n ₊ 2 v ( 1 - u - v ) + ... + C n + 2 vⁿ - ² ( 1 - u - v )

• •    и так далее...

• •    если решение одного из арбитров попало в L (c вероятностью C 2 n _{+ 1} u ), а другие 2n решения не попали ₂ни в L , ни в R , вероятность этого ( 1 - u - v ) n .

Следовательно, вероятность выбора y равна n+1, x

P1 = z cn++1 un+-(1 - u) n'+1 + l=1

nI

+z C2n+1 ui Z C2^n+1-ivj (1 - u - v)2nti"‘"J i=1

Аналогично, вероятность выбора x равна n+1                         n - i+1

P2 = Z сK++1 vn+i (1 - u)

i = 1

ni

+ Z C in + 1 v i Z C 2n + 1 - i u j ( 1 - u - v ) n ⁺ - i - ^J .

i=1

В остальных случаях будет x + y

.

Таким образом, функция выигрыша в данной игре имеет вид x x + y

^{H ( x} , y ) = -y ⁺

_Y_ n + 1

⁺ -y Z ^C 2nn = 1 ( v n ^{+ i (1} - v ) n " ^{+ 1-} u n ^{+ i (1} - u ) n " ⁺¹)⁺ (1)

² i = 1

+ Z C 2n + 1 Z C 2n + 1 - i ( 1 - u - v ) 2 n ^{+ 1} i ^J ( v i u ^J - v ^J u i ) i = 1          J = 0

Обозначим выражение в квадратных скобках равенства (1) как S(v, u) . Легко видеть, что S(v, u) антисимметрична, то есть S(v, u) = –S(u, v) . Тогда для v = u имеем S(u, u) = 0 .

Чтобы найти равновесие, продифференцируем (1) по x и y. Получим dH dx

= - + -S (v, u) +

x - y

d S d v

[ f ( x ) - 2 ^f

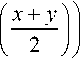
1 d S x + y )

+ f

2 d u ( 2 )

и dH 1 1 x

= ^^- ^^S ( ^v , u ) d y 2 2

-

x - y 1 d S

2 d v

.

Ограничимся рассмотрением симметричного случая, когда распределение F(x) имеет симмет- ричный вид относительно нуля. Тогда из симметрии следует, что в равновесии x = –y и u = v. Тогда из системы д H к=0

^H = 0. ду

находим условие для равновесия. Заметим, что поскольку S(v, u) = –S(u, v) , то

д S (v, и)     д S (и, v)

д v   “     д и"

Отсюда при u = v и x = –y вытекает

2 + х (f (х)-f (0))^^ = 0.(2)

Из (1) находим дS(v,v)

(     = EC2-+1E C2-+1- (1 - 2v)     j (i - j) v ■ j-1 + д v        i=1

- + 1

+ E C 22-+ 1 v i ^{+ j - 1} ( 1 - v ) "”‘ ( ( - + i ) ( 1 - v ) - ( - - i + 1 ) v ) .

= 1

Равенства (2)–(3) могут быть использованы для вычисления численных значений оптимальных стратегий в данной игре.

В таблице приведены вычисленные оптимальные стратегии для различных n. Можно заметить, что при увеличении числа арбитров оптимальные стратегии сходятся.

Данная работа выполнена при финансировании Аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы» (проект 1.8.10) и при поддержке Российского фонда фундаментальных исследований (проект № 09-01-90709-моб_ст).

Оптимальные ст				ратегии игроков в зависимости от числа арбитров
n	0	1	2	3	4	5	6	7	8	9	10
x* y*	1.667 -1.667	1.352 -1.352	1.203 -1.203	1.111 -1.111	1.047 -1.047	1.000 -1.000	0.962 -0.962	0.932 -0.932	0.906 -0.906	0.884 -0.884	0.864 -0.864