Модифицированная теория неупругости

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2025PNRPU MECHANICS BULLETIN

Вопросам построения математических моделей при термовязкопластическом деформировании конструкционных сталей и сплавов посвящено большое количество работ. Основные направления построения теорий и обширную библиографию по этому вопросу можно найти в работах А.А. Ильюшина [1; 2], В.В. Новожилова [3], Ю.Н. Работнова [4], И.А. Биргера [5], В.С. Бондаря [6–9], Ю.И. Кадашевича [3], Л.М. Качанова [10], Ю.Г. Коротких [11; 13], И.А. Волкова [11–14], Л.А. Игумнова [12–14], Н.Н. Малинина [15], Кремпла [16; 17], Криега [18–20], Миллера [21–23], Оно [24–27], Шабоша [28–32] и др.

Наибольшее распространение в практических расчетах нашли варианты теории течения при комбинированном упрочнении, применяемые в конечноэлементных программных комплексах на основе моделей Шабоша [28–32], Коротких [11; 13] и Бондаря [6–9]. Эти модели являются наиболее экспериментально обоснованными и широко применяемыми в расчетах ресурса материалов конструкций при термовязкопластическом деформировании в условиях повторности и длительности воздействия термомеханических нагрузок. Следует отметить, что в вариантах моделей Шабоша и Коротких деформация разделяется на упругую, пластическую и ползучести, а в варианте модели Бондаря – на упругую и неупругую. Поэтому первые варианты относятся к теории термовязкопластичности, а последний – к теории неупругости. Следует отметить, что разделение необратимой деформации на деформации пластичности и ползучести весьма условно. При быстрых процессах деформации ползучести малы, и деформирование считается пластическим, при медленных процессах необратимая деформация едина, и разделение ее на пластическую и ползучесть весьма условно. Поэтому целесообразно говорить о разделении деформации на упругую (обратимую) и неупругую (необратимую).

В последнее время большое внимание уделяется несимметричным мягким циклическим процессам нагружения, так как при таких процессах нагружения происходит смещение петли циклического гистерезиса, т.е. одностороннее накопление деформации. Данное явление получило название ratcheting, или вышагивание, и оно приводит [33; 34] к существенному снижению ресурса материала по сравнению с жестким нагружением с таким же размахом циклических деформаций. При несимметричном жестком циклическом нагружении происходит посадка петли циклического гистерезиса, но это явление практически не сказывается на ресурсе материала, поскольку размах деформации не изменяется и смещения петли нет.

Попытки описания явления вышагивания (ratcheting) имеют место в моделях Шабоша [31; 32; 35–40], Коротких [11; 41; 42] и Бондаря [7; 9; 43–46]. В вариантах модели Шабоша вводятся [31; 32; 35–40] дополнительные уравнения для микронапряжений и увеличивается число подгоночных параметров. В вариантах модели Коротких вводятся [11; 41; 42] разные поверхности памяти и дополнительные микронапряжения. В вариантах модели Бондаря также вводится [45–46] поверхность памяти и эволюционные уравнения для материальных параметров. Сравнительный анализ этих подходов для пластического деформирования проводится в работах [47; 48]. В рамках модели Бондаря в работах [7; 44; 47; 48] рассматривается простейший подход к описанию явления вышагивания (ratcheting) и посадки петли при упругопластическом циклическом деформировании. Модификация модели неупругости сводится к тому, что определяющая (материальная) функция уравнения для микронапряжения первого типа не является константой, а зависит от накопленной пластической деформации. В настоящей работе приведен вариант модели неупругости, основанный на теории Бондаря, разделяющий процессы монотонного и циклического деформирования. Предложенный вариант позволяет описывать процессы неупругого деформирования, возникающие при переходе от монотонного нагружения к циклическому и наоборот.

В данном исследовании рассматриваются основные положения и уравнения модифицированной теории не-упругости. Приводятся соотношения, связывающие определяющие функции с материальными. Дается перечень материальных параметров и функций, подлежащих экспериментальному определению. Формулируется базовый эксперимент и метод определения материальных параметров и функций. Приводятся материальные параметры и функции бронзового сплава БрХ08-Ш при температурах 20, 400, 500, 600 °С. Проводится верификация теории при циклическом изотермическом деформировании вплоть до разрушения (малоцикловая прочность) в условиях высоких температур. Рассматривается также ползучесть и длительная прочность при изотермических и неизотермических нагружениях. Результаты расчетов сопоставляются с результатами экспериментов.

Основные положения и уравнения

Рассматриваются малые деформации и повороты однородных и начально изотропных поликристалличе-ских конструкционных сталей и сплавов при темпера- турах, когда нет фазовых превращений, и скоростях деформаций, когда динамическими эффектами можно пренебречь. Тензор скоростей деформаций eij пред- ставляется в виде суммы тензоров скоростей упругой

Е j и неупругой Е in деформаций:

e in

^Е j   ^E j + ^E j •

Упругие деформации описываются обобщенным на неизотермическое нагружение законом Гука:

^Е J = E ^{[ (r - v} ( 3< 7 0 ⁸ j ^-a j ) ] + ^a J T       (2)

a ET =a T 8j - Er [cj-v(3c8-Cj )] X dE x— dT

^- -1 1 3 ^{G 8}

E

-

_ \ d v с I — ^j ) dT

где E ( T ) , v ( T ) , a _T ( T ) - модуль Юнга, коэффициент Пуассона, коэффициент температурного расширения; 8 j - символ Кронекера; T - температура; C j - тензор напряжений; с ₀ = с ii /3 - среднее напряжение.

Для разделения упругого и неупругого деформирования в пространстве напряжений вводится поверхность нагружения, которая изотропно расширяется или сужается и смещается в процессе нагружения. Уравнение поверхности нагружения принимается в следующем виде:

f (с J )=2 Sj ’ Sj ’ - С2 = 0.             (3)

*

^S j = sj- a j •

Здесь s_ij , s_ij ^* , a_ij – девиаторы напряжений, активных напряжений [3], микронапряжений [3]. Скаляр C отвечает размеру (радиусу) поверхности нагружения и характеризует изотропное упрочнение (разупрочнение), а девиатор микронапряжений a_ij характеризует смещение поверхности нагружения, т.е. направленное (анизотропное) упрочнение. Тензор смещения a_ij и радиус C являются функционалами процесса нагружения.

Для радиуса поверхности нагружения принимается следующее эволюционное уравнение:

"in .

^С = q s ^£ u* ^{+ q}T^{T - q}R ,

2 - - in in

₃ ^ε ij ^ε ij

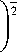
Здесь εiun* – длина дуги траектории неупругой деформации (накопленная неупругая деформация); ЕП -скорость накопленной неупругой деформации; qЕ, qT, qR - определяющие функции, которые далее бу- дут выражены через материальные функции, подлежащие экспериментальному определению. Функция q£ отвечает механическому упрочнению (разупрочнению), qT обеспечивает неизотермический переход, а qR – возврат механических свойств при отдыхе, отжиге.

Смещение поверхности нагружения определяется следующим эволюционным уравнением:

a , = 3g e J + ( 3g _E s J + g „ a ,, ^ £ U * + ⁺ ( 3g I ^s in ^{+ g} Ta^aiJ T - ^ 3^g E ^s J ^{+ g} R a j ^j ■

Здесь g, g _E , g _a , g T , g T , g ^R , g ^R - определяющие функции, которые далее будут выражены через материальные функции, подлежащие экспериментальному определению. Первые три слагаемых в уравнении (5) описывают процессы образования и снятия микронапряжений при неупругом деформировании. Далее будут приведены модифицированные определяющие функции этих слагаемых для описания процессов посадки и вышагивания (ratcheting) при циклических нагружениях. Два следующих слагаемых обеспечивают неизотермический переход, а два последних – снятие микронапряжений при отдыхе, отжиге.

Эволюционное уравнение (5) соответствует представлению [7; 9; 44] микронапряжений в виде суммы микронапряжений 1-го и 2-го типов, для которых имеют

место уравнения:	a9 =a,  + a, 2 , ij         ij          ij	(6)
	( 1 )       2 ( 1 ) in aJ = 3g Е ij ’	(7)
a ( 2)= 2 g( 2 ) i ‘ n aij     3g ε ij	22     T 22    R 22 + g( )a(- 's , + g ( 'a( )1 —s ( )a(. . g a ij u * g a     ij        g a     ij .	(8)

Смещение центра поверхности нагружения согласно принципу суммирования микронапряжений Новожилова – Шабоша [3; 32] определяется уравнением (6). Микронапряжения 1-го типа согласно модели Ишлин-ского – Прагера – Кадашевича – Новожилова [3; 49–52] определяются уравнением (7). В уравнении (7) для описания процессов посадки и вышагивания (ratcheting) определяющая функция g ^{( 1 )} принимается [7; 44] при циклическом и монотонном деформировании зависящей не только от температуры, но и от накопленной неупругой деформации. Эта модификация позволяет существенно расширить возможности теории неупругости. Для определения микронапряжений 2-го типа используется модель Армстронга – Фредерика – Кадашевича [53; 54], обобщенная [6; 7; 9] на неизотермические процессы и процессы, развивающиеся во времени.

При деформировании материалов могут иметь место как монотонные, так и циклические режимы нагружения, каждый из которых имеет свои особенности [9; 45; 46]. Для разделения процессов монотонного и циклического деформирования в пространстве тензора неупругих деформаций ε ⁱ _ij ⁿ вводится поверхность памяти, ограничивающая область циклического деформирования. Поверхность определяется положением ее центра ^ , и ее радиусом (размером) С _Е ■ Уравнение поверхности памяти принимается в следующем виде:

F ( ^е у ) = 3 ( ^е П — S J )( ^е J — S J ) — С _Е = 0. (9)

Для вычисления положения центра и размера поверхности памяти вводятся два тензора неупругой деформации, е ‘П ^{( 1 )} и е ‘П ^{( 2 )} , определяющие границы поверхности. В начале деформирования эти переменные равны нулю. Определение смещения и размера поверхности памяти происходит в момент смены направления неупругого деформирования. В качестве критерия смены направления принимается следующее условие:

in in

^Eij ( t - 0 ) ^EiJ <  °’

где е J - тензор скоростей неупругой деформации в текущий момент времени t ; Е nt — ° ) - тензор скоростей неупругой деформации в предшествующий ( t -0 ) момент времени t .

В момент времени t координаты центра и размер поверхности памяти вычисляются на основании следующих соотношений:

Е in (1) + Е in (2)

_Е ⁱⁿ ( ² )    _Е‘" ( ¹ ) _Е ‘" ( ¹ ) _ p in s _ ij          ^J

^Е ,       ^Eij , ^Е‘,       ^Е, , S ,                      ,

С _E =

( jn ( ¹ ) -_Fⁱⁿ ( ² ) A ^ε ij ^ε ij

( jn ( ¹ ) -_Fⁱⁿ ( ² ) A ^ε ij ^ε ij

\

Тогда условием циклического деформирования является деформирование в пределах поверхности памяти F ( e J ¹) <  0, а условием монотонного деформирования - F ( Е in ) > 0.

Для определения скоростей неупругой деформации используется ассоциированный с (3) градиентальный закон течения:

*

• in _ df Л _ ³ s j пн *

EJ ,    Л   n £u* ’ °u i   d °ij     2 ° u

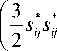
Здесь ° U - интенсивность активных напряжений.

Используя уравнения (1)-(5) и (12), можно получить уравнения для скорости накопленной неупругой деформации при мягком (заданы напряжения) и жестком (заданы деформации) нагружениях:

е“ u *

E *

* ■

- — - B T T' + b^r

2 ° u

’

_ д Ср       с Э Ср qe аг" ’ qT С Э T ’ qR qe Pc ’ u *               p g = Ea + ° a в’ ge=|Er + в Ea ’ g a = -в’ de u *

T T = dEa - Ea d ° a „T = 1 d ° a ge   dT ° a dT ’ g a ° a dT ’

in е u *

E * + 3 G

3G

*

° u

- B T T + B R

in *             *

^E * = q e ⁺ g ⁺ g _EE u ⁺ g a a u ’

П T            T in *      T *

^B = ^qT ^{+ g} e ^e u ^{+ g} a a u ’ R        R^* * R^K /,*

B = qR + geeu + gaau ’ si* ein   . 3 sia _ E         Гx, если x > 0,

= Л^, a_u = —^J-G, G = —---- , x = 1

о 2 о 2(1 +v )      [ 0, если x <  0.

P ge = gePa ’ ga =(g + gaau )--- ’ au

_ a _ t _W dW , ^g ю = ¹ ’ ^g W = ^P ’ ^g W =         ’

W , dT

a =

\ n a

.°- I _aw ₌l Iyy²⁾ 1 ²

( 2 )        ’ a u       I о a i— a ij | ’

I au’ J        V ^{2        J}

E„ =Ea a 1 + KE (e un*-e un*( mc)

■pp при F ( ^e in )< 0,

Скорость накопленной неупругой деформации всегда равна нулю (упругое состояние), если изображающая точка процесса нагружения находится внутри поверхности нагружения, т.е.

o u <  С - упругость. (15)

При нахождении изображающей точки процесса нагружения на поверхности нагружения (3) состояние возможно как упругое, так и неупругое, и это состояние определяется знаком вычисляемой скорости накопленной неупругой деформации: скорость отрицательная -состояние упругое, скорость положительная - состояние неупругое.

Для описания процесса накопления повреждений принимается [6-9; 43; 44] кинетическое уравнение, основанное на работе микронапряжений 2-го типа на поле неупругих деформаций и обобщенное на неизотермическое нагружение и процессы залечивания и охрупчивания:

a-1 a (2)pin ю = aю а • ——'— - gю, (16) Wω

W = g T T - g _wW , (17) a — ⁾ = a — ^- a ⁽¹⁾ = a — ^- 3 g ^{( 1 ) e} in ’ g ^{( 1 )} = E a .

Здесь W - энергия разрушения; a ,g „ , g W ,g w -определяющие функции, которые далее будут выражены через материальные функции, подлежащие экспериментальному определению.

Связь определяющих функций с материальными

Определяющие функции выражаются через материальные следующим образом:

E a = ^Ea ( cm ) + ( ^Ea 0

in in

^{( e} u *     ^e u * ( cm )

λ

( cm )

при F ( e in ) > 0,

x при x <  1, 1 при x >  1,

P c = exp ( Ъ_с ) | C - С р 0 | ^{n c} ( 1 - " )’ m " ,

^Pa = exP ( ^ba )( a u ) n a ( 1 - "  Г m " ’

^ I 0, если ° >  0, [ ^exP ( bi MT ’ ^если °« <  ⁰’

P = ^eXP ( ^Ъ p ) ( ° u ) n ^P ’

.           X 1/           / X 1/

( 3      I^/2        ( 3      ^/2

^au = 1 2 a — a — J ’ ° u = I ^ s i s J ’ ^cp 0 = ^cp ( ^{T ,0} ) = ° - 1 ■

Здесь e u "( _mc ) , e u * ( cm ) - значения накопленной неупругой деформации в момент смены монотонного деформирования на циклическое и наоборот циклического на монотонное; E a ( cm ) - значение параметра E_a в момент смены циклического деформирования на монотонное; i ( с _т ) -величина накопленной неупругой деформации, при которой параметр E_a достигает значения E_{a 0} ( \ _ст ) = 0,005 + 0,01); ° _ j - предел длительной прочности (предел ползучести), n _a - параметр нелинейности процесса накопления повреждений, который практически для всех конструкционных сталей и сплавов равен 1,5.

Таким образом, модифицированную теорию неупру-гости замыкают следующие материальные функции:

E ( T ) , v ( T ) , a _T ( T ) - упругие параметры;

C p ( T , e“* ) - функция изотропного упрочнения;

Ea0 (T),Oa (T),p(T)   - модули анизотропного упрочнения;

K_E ( T ) , n_E ( T ) - параметры посадки и вышагивания;

W 0 ( T ) - начальная энергия разрушения;

b_C ( T ) , n_C ( T ) - параметры изотропной ползучести;

b a ( T ) , n a ( T ) - параметры анизотропной ползучести;

т _ш ( T ) - параметр разупрочнения при ползучести;

b ( T ) , n _} ( T ) -параметры залечивания;

b _p ( T ) , п _р ( T ) - параметры охрупчивания.

Базовый эксперимент и метод определения материальных параметров и функций

Вначале определяются материальные параметры и функции (первые 10 параметров и функций) при упругопластическом деформировании в условиях одноосного напряженного состояния при различных температурах. Скорость деформирования должна находиться в интервале 10^-2 ^ 10^-3 с^-1, т.е. деформирование должно проходить без влияния реологических и динамических эффектов.

Для определения материальных параметров и функций термопластичности необходимы следующие результаты экспериментальных исследований:

• –    упругие параметры, которые определяются традиционными методами (справочные данные);

• –    диаграмма монотонного деформирования до деформации 0,03 ^ 0,05 после жесткого предварительного циклического деформирования с размахом 0,01 ^ 0,02 (5 ^ 10 циклов до стабилизации);

• –    размахи напряжения при жестком циклическом деформировании до монотонного и после монотонного нагружения;

• –    число циклов до разрушения при жестком циклическом деформировании;

• –    процесс посадки петли упругопластического гистерезиса при жестком циклическом нагружении после монотонного деформирования.

Все эти результаты могут быть получены при проведении следующего базового эксперимента, состоящего из трех этапов:

• –    жесткое циклическое нагружение при среднем значении деформации Е ^ = 0, размахе деформации Де^{( 1 )} = 0,01 + 0,02 и числе циклов N *') = 5 + 10 до практической стабилизации размаха напряжения;

• -    монотонное растяжение до е^{( 2 )} = 0,03 + 0,05 ;

„( 3 )     „( 2 )

• -    жесткое циклическое нагружение при е' m' = Е' ' и Де = 0,01 + 0,02 до разрушения.

Метод определения материальных параметров и функций термопластичности по результатам этого базового эксперимента изложен в работах [6–9].

Для определения остальных 9 материальных параметров термоползучести необходимы следующие экспериментальные результаты при ползучести в условиях одноосного напряженного состояния при различных уровнях напряжения и температуры:

• Е ¹" - деформация разрушения только за счет ползучести;

• Е П - начальная скорость ползучести;

• t p - время разрушения при растяжении;

• t p - время разрушения при сжатии.

Все эти результаты могут быть получены при проведении следующего базового эксперимента:

• –    ползучесть при постоянном напряжении растяжения (3–5-го уровней) в условиях кратковременной ползучести;

• –    ползучесть при постоянном напряжении растяжения (3–5-го уровней) при установившейся ползучести;

  – ползучесть при постоянном напряжении сжатия (1–2-го уровня) в условиях кратковременной или установившейся ползучести.

Далее рассматривается метод определения материальных параметров термоползучести по результатам базового эксперимента. Параметр разупрочнения m _ω определяется [6–9] на основе следующего соотношения, используя результаты при кратковременной ползучести:

Е in mm = —p- -1.               (18)

• ^ш с^1П /⁺

• ^Е 0 tp

Для определения функций изотропной P_C и анизотропной P_a ползучести и соответствующих материальных параметров b_C , n_C , b_a , n_a необходимы значения начальной скорости ползучести при различных уровнях напряжения растяжения. Вначале, зная материальные параметры термопластичности, вычисляются значения радиуса C и микронапряжения a для различных уровней напряжения о , т.е. устанавливается соответствие между начальной скоростью ползучести Е П и радиусом С , а также между Е П и микронапряжением a .

Pc =Е0n, exp (bc )| C - Cp0|nс =Е0, be + nc ln\C-Cp0I = In(Е0n),             (19)

Pa =E in, exp (ba)(a) na =E 0, ba + na ln (a) = ln(E0n).                 (20)

Из линейных зависимостей (19) и (20), построенных на основе метода наименьших квадратов, можно получить материальные параметры изотропной и анизотропной ползучести.

Для определения материальных параметров охрупчивания необходимы экспериментальные данные по деформации разрушения только за счет ползучести и времени разрушения при различных уровнях напряжения растяжения. Тогда модуль охрупчивания ρ вычисляется [6–9] по следующей формуле:

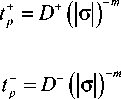
1 W

P = —ln--—, t+    a eP

Модуль залечивания λ определяется по следующей формуле:

а материальные параметры охрупчивания определяются из линейной зависимости bp+ np ln (o) = ln (p),                (22)

построенной на основе метода наименьших квадратов.

Для определения материальных параметров залечивания необходимы экспериментальные данные по длительной прочности при растяжении и хотя бы одно значение времени до разрушения при сжатии. Степенные законы длительной прочности при растяжении и сжатии имеют следующий вид:

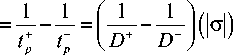
Тогда материальные параметры залечивания будут вычисляться по формулам:

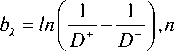
= m ,

В табл. 1 и 2 приведены полученные по результатам базового эксперимента материальные параметры и функции бронзового сплава БрХ08-Ш при четырех уровнях температуры 20, 400, 500, 600 °С.

Материальные функции сплава БрХ08-Ш

Таблица 1

Table 1

Material functions of BrKh08-Sh alloy

Т , ° С	Е , МПа	ν	α Т , 1/град	Е а 0 , МПа	О a , МПа	в	W 0 , Дж/cм3
20	133 000	0.3	1,7·10-5	500	142	460	112
400	110 000	0.31	2.16E-05	1400	82	800	1700
500	90 000	0.31	2.16E-05	1500	45,7	810	1300
600	90 000	0.31	2.16E-05	1200	27,4	1030	200

Таблица 1

Продолжение

Table 1

Extention

K E	nE	bC	nC	b a	na	b λ	n λ	b P	n P	m ω
40	-0,3	-100 000	1	-100 000	1	-100 000	1	-100 000	1	1
40	-0,3	-22,2	4,98	-45,9	9,19	-56,2	10,1	-29,3	5,5	3
40	-0,3	-22,3	3,47	-24,5	4,72	-32,4	5,3	-24,8	5	3
40	-0,3	-11,8	1,17	-12,8	1,63	-9	1,07	-9,89	2	3

Таблица 2

Функция изотропного упрочнения сплава БрХ08-Ш C p ( e“, T ) , МПа

Function of isotropic hardening of the BrKh08-Sh alloy C_p ( e“* , T ) , MPa

Table 2

T , ° С/ e u *	0	0,0005	0,0015	0,003	0,01	0,019	0,043	0,092
20	78	185	185	185	185	185	185	195
400	70	101	101	102	105	123	125	130
500	40	112	112	112	112	112	112	112
600	30	52	69	70	72	75	74	74

Таблица 2

Продолжение

Table 2

Extention

0,14	0,26	0,39	0,5	0,8	1	1,7	2,3
205	217	222	221	218	217	212	205
135	131	131	132	131	130	127	127
111	110	110	109	107	106	104	102
74	74	73	73	72	72	70	69

Циклическое деформирование и малоцикловая прочность в условиях высоких температур

Для тестирования модифицированной теории не-упругости при циклическом деформировании вплоть до разрушения в условиях малоцикловой усталости проведены испытания гладких цилиндрических образцов из бронзового сплава БрХ08-Ш. Испытания проводились при температурах 400, 500 и 600 °С. Нагрев образцов осуществлялся в муфельной печи с контролем температуры образца. На рис. 1 изображен чертеж образца.

Испытания образцов проведены в соответствии с ГОСТ 25.502 при симметричном жестком (с контролируемой деформацией) циклическом растяжении – сжатии. Скорость нагружения при испытаниях составляла 5 циклов в минуту. Испытания проведены до разрушения с регистрацией количества циклов до разрушения, диаграмм циклического деформирования и зависимостей размаха напряжения от номера цикла. Число циклов до разрушения определяется фиксацией трещины или моментом катастрофического падения размаха напряжений.

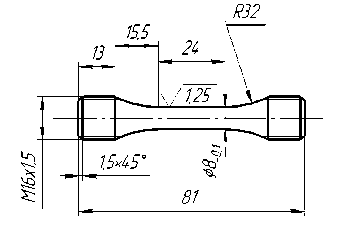
Рис. 1. Чертеж образца из сплава БрХ08-Ш для испытаний на циклическое деформирование

Fig. 1. Drawing of a sample made of BrKh08-Sh alloy for testing for cyclic deformation

На рис. 2 экспериментальные данные по циклическому деформированию образцов при 400 °С на 40-м цикле обозначены синими ромбами, а расчетные – синей линией; при 500 °С на 40-м цикле – оранжевыми квадратами и оранжевой линией, при 600 °С на 60-м цикле – зелеными кружками и зеленой линией. Размах деформаций при 400 °С составляет 0,016; при 500 и 600 °С – 0,01, а скорость деформации соответственно – 2,7·10-3 и 1,7·10-3 с-1. Расчетное число циклов до разрушения при 400 °С равно 68 циклов, а экспериментальное – 82 цикла; при 500 °С – 76 и 74 цикла; при 600 °С – 95 и 124 цикла.

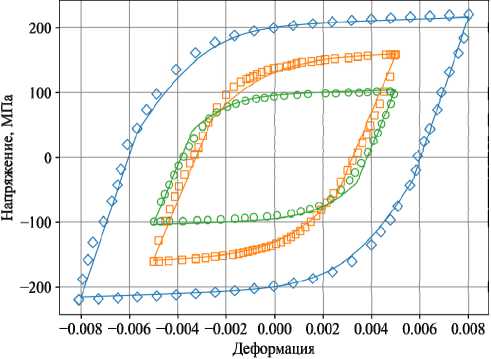
Рис . 2. Экспериментальные и расчетные диаграммы циклического деформирования образцов из сплава БрХ08-Ш при 400, 500 и 600 °С

Fig. 2. Experimental and calculated diagrams of cyclic deformation of samples from the BrKh08-Sh alloy at 400, 500 and 600 °C

Сравнение расчетных и экспериментальных результатов показывает, что отличие циклических диаграмм не превышает 10–15 %, а число циклов до разрушения – 30 %.

Ползучесть и длительная прочность при изотермических и неизотермических нагружениях

Для тестирования модифицированной теории не-упругости в условиях ползучести вплоть до разрушения проведены эксперименты по длительному нагружению образцов сплава БрХ08-Ш. Чертеж образца представлен на рис. 3.

Испытания проводились в соответствии с ГОСТ 3248-81. При постоянной нагрузке и постоянной температуре измерялось относительное удлинение образца с помощью навесного экстензометра с базой 25 мм. Испытания проведены при температурах 400, 500 и 600° С и трех уровнях напряжения для каждой температуры. По результатам испытаний фиксировалась зависимость деформации от времени вплоть до разрушения.

На рис. 4 приведены расчетные и экспериментальные диаграммы ползучести вплоть до разрушения при температуре 400° С и трех уровнях напряжения. Для каждого уровня напряжения испытаны по два образца.

Экспериментальные данные, приведенные на рис. 4, при напряжении 133 МПа обозначены оранжевыми кружками и квадратами, а расчет – оранжевой линией, при напряжении 151 МПа – зелеными кружками, квадратами и зеленой линией, при напряжении 158 МПа – красными кружками, квадратами и красной линией.

На рис. 5 приведены диаграммы длительной прочности. При температуре 400° С экспериментальные точки обозначены синими ромбами, а расчет – синей линией ; при 500 ° С – оранжевыми квадратами и оранжевой линией; при 600 °С – зелеными кружками и зеленой линией.

Из анализа диаграмм ползучести следует, что деформация разрушения заметно уменьшается (практически в четыре раза) за время порядка 100 мин. Это говорит о значительном охрупчивании бронзового сплава при его деформировании в условиях высоких температур.

Сравнение расчетных и экспериментальных результатов показывает, что отличие диаграмм ползучести и длительной прочности не превышает 30 %.

Для исследования процессов ползучести при неизотермическом нагружении был проведен следующий эксперимент. Ненагруженный образец сплава БрХ08-Ш нагревался до 400 °С. Затем образец растягивался до напряжения 76,6 МПа и выдерживался 15 мин при температуре 400 °С. В следующие 10 мин температура повышалась до 550 °С, а затем в следующие 10 мин – до 600 °С. Время выдержки при 600 °С составляло 15 мин, после чего образец охлаждался и разрушился через 15 мин при температуре 440 °С. В результате были получены зависимости температуры и деформации от времени.

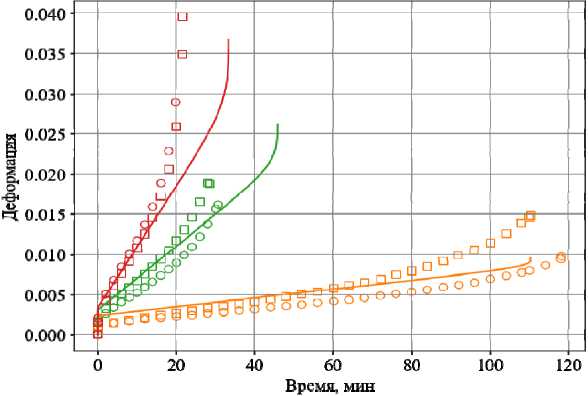
Рис. 4. Диаграммы ползучести образцов из сплава БрХ08-Ш при напряжениях 133, 151 и 158 МПа

Fig. 4. Creep diagrams of samples from BrKh08-Sh alloy at stresses of 133, 151 and 158 MPa

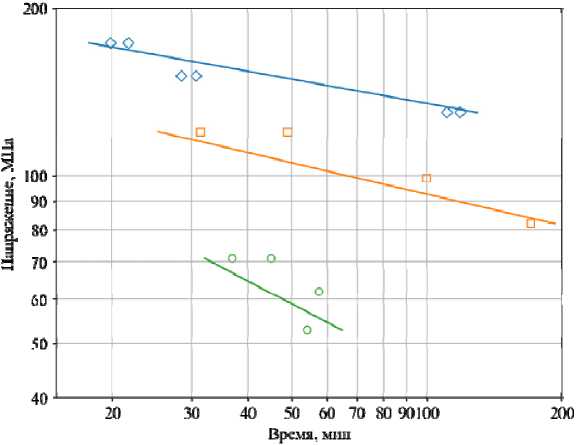
Рис. 5. Диаграммы длительной прочности образцов из сплава БрХ08-Ш при 400, 500 и 600 °С

Fig. 5. Diagrams of long-term strength of alloy samples BrKh08-Sh at 400, 500 and 600 °C

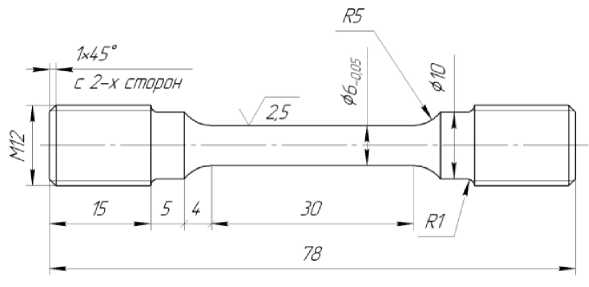
Рис. 3. Чертеж образца из сплава БрХ08-Ш для испытаний на ползучесть

Fig. 3. Drawing of a sample made of BrKh08-Sh alloy for creep testing

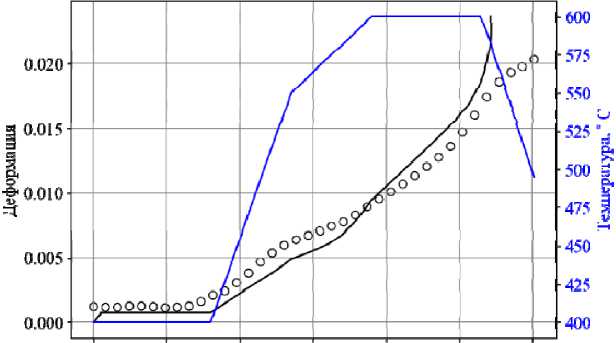
На рис. 6 синей линией показано изменение температуры от времени, черной линией – расчетное изменение полной деформации, а черными кружками – экспериментальные значения полной деформации. Расчетное время разрушения составило 54 мин, а экспериментальное – 60 мин.

Сравнение расчетных и экспериментальных результатов показывает, что отличие деформаций ползучести и времени до разрушения не превышает 10–15 %.

О 10      20      30      40      50      60

Время, мин

Рис. 6. Зависимость полной деформации от времени для образцов из сплава БрХ08-Ш

Fig. 6. Dependence of total deformation on time for samples made of BrKh08-Sh alloy

Заключение

Изложены основные положения и уравнения модифицированной теории неупругости, которая интегрирована в конечно-элементный комплекс для практических расчетов выработанного и остаточного ресурса материала конструкций в условиях повторности и длительности воздействия термомеханических нагрузок. Для описания процесса несимметричных циклических нагружений и возникающих при этом эффектов посадки и вышагивания (ratcheting) петли циклического гистерезиса проведена модификация эволюционных уравнений для микронапряжений.