Модифицированные алгоритмы построения нейронной сети SOFM

Неослабевающий интерес к проблеме построения адаптивных сеток обусловлен необходимостью получения достоверного численного решения прикладных задач при сохранении умеренных требований к вычислительной технике. Основная идея методов построения адаптивных сеток состоит в уменьшении размеров ячеек в зонах расчетной области, соответствующих значительным ошибкам решения.

Для построения адаптивных сеток с заданной плотностью применяются следующие традиционные методы эквираспределения [1], Томпсона [2], эллиптический метод [3], алгебраические методы [4], конформных отображений [5] и т.д. В основе применяемых методов лежат теории дифференциальных уравнений, вариационного исчисления и многомерной дифференциальной геометрии. Для получения качественных адаптивных сеток все эти методы требуют решения сложных систем нелинейных дифференциальных уравнений с частными производными, что накладывает ряд известных ограничений.

В настоящее время способность построения адаптивных сеток с заданной плотностью на сложной физической области демонстрируют нейросетевые алгоритмы [6], [7], [8], [9], [10] и т.д. Развитие современных нейросетевых моделей обязано классической теории самоорганизующихся карт Кохонена (сеть SOFM - Self-Organizing Feature Maps, T.Kohonen) (например [11], [12]). Соревновательная нейронная сеть SOFM с обучением без учителя выполняет задачу проецирования многомерного пространства в пространство с более низкой размерностью (чаще всего двумерное). Дискретно-стохастический подход, присущий обучению нейросетей, обеспечивает привлекательность в отношении простоты алгоритмов, возможностей их эффективного распараллеливания, отражения плотности распределения данных в области и отсутствия привязки к размерности отображаемого пространства.

Как известно [9], применение базовой модели SOFM приводит к появлению граничного эффекта, наличию мертвых нейронов и нарушению гладкости сетки. Для решения указанных проблем предложены модифицированные методы, в основе которых лежит идея чередования базового алгоритма для внутренних и внешних узлов [7], использования так называемых раскрашенных моделей и специальных алгоритмов сглаживания [9]. Кроме того, в алгоритмах усовершенствованы функции соседства нейронов. Эта функция представляет собой невозрастающую функцию от дискретного времени и расстояния между нейроном-победителем и соседними нейронами в сетке. Функция соседства нейронов разбивается на две части: собственно функцию расстояния и функцию скорости обучения. Изменение параметров функций расстояния и скорости обучения относительно дискретного времени обеспечивает качество адаптации сетки на области. Как правило, приемлемая адаптация сетки наступает в результате многочисленных вычислительных экспериментов по выбору параметров функции соседства нейронов. В то же время рекомендации по характеру функций расстояния и скорости обучения носят достаточно общий характер и незначительно облегчают поиск оптимальных параметров.

В данной работе, помимо представления краткого обзора существующих нейросетевых алгоритмов адаптации регулярных сеток на плоскую область, предпринята попытка формулировки рекомендаций по выбору параметров функции соседства, включающей Гауссову функцию расстояния для модифицированного алгоритма SOFM.

Основные идеи

Самоорганизующаяся карта признаков имеет набор входных элементов, число которых соответствует размерности учебных векторов (пространства физической области), и набор выходных элементов, которые служат в качестве прототипов и называются кластерными элементами (узлы сетки). Входной слой элементов передает сигналы кластерным элементам при помощи взвешенных связей. Весовые значения связей интерпретируются как значения координат, описывающих позицию кластера в пространстве образцов. В начальный момент дискретного времени кластерные элементы могут определяться как случайными координатами пространства образцов, так и в заданных вершинах регулярной решетки, например, с треугольными, квадратными или шестиугольными краями. В процессе обучения веса нейронов настраиваются, в результате чего сетка, самоорганизуясь, постепенно растягивается по заданной физической области.

Работа сети SOFM характеризуется этапом инициализации карты и циклом:

• 1)    выбор случайного образца x ( n ) с заданной плотностью распределения;

• 2)    нахождение узла победителя (best matching unit, BMU) – кластера на карте признаков, вес которого имеет меньшее отличие в заданной метрике от случайного образца;

• 3)    корректировка узлов из числа близлежащих к победителю – изменение веса победителя и его соседей с целью приближения к случайному образцу;

• 4)    определение ошибки карты.

При определении узла победителя в шаге 2, как правило, в качестве метрики выбирается Евклидово расстояние d . В редких случаях используют угол между радиус-векторами узла претендента и случайного образца.

Корректировка положений узлов шага 3 происходит в зависимости от степени близости к победителю c помощью функции соседства 0 ( n , i BMU , j_BMU , i , j ) по формуле:

w j ( n + 1 ) = w j ( n ) + q ( n, l _BMU , j BMu , i , j ) • ( x ( n ) - w j ( n ) ) ,                         (1)

где n – номер итерации, w_ij – вес ij -го узла, x ( n ) – случайно выбранный образец, i_BMU j_BMU - индекс узла победителя для образца x ( n ) .

Функция соседства представляет собой невозрастающую функцию от дискретного времени n и расстояния между нейроном-победителем и соседними нейронами в сетке. Как описано выше, эта функция разбивается на две части: функцию расстояния h ( d, n ) и функцию скорости обучения ^ ( n ), т.е.

q (n , i BMU , j BMu , i , j ) = ⁵ ( n ) " h ( d , n ).

Обычно применяется одна из двух функций расстояния:

h ( d , n )

const, d <  ff ( n ) 0, d >  ^^n )

– ступенчатая функция

или функция Гаусса

- d ²

h ( d,n ) = e 2 ° 2 ⁽n ⁿ ) .

Лучший результат при адаптации сетки на сложной области показывает функция Гаусса. Функция ° ( n) называется радиусом обучения, который выбирается достаточно большим на начальном этапе обучения и постепенно уменьшается так, что в конечном итоге обучается один нейрон-победитель. В качестве радиуса обучения используют линейно или экспоненциально убывающую функцию от времени, например, в работе [8]

° ( n) = a • n ^{- 0.2} , (3)

где величина a выбирается таким образом, чтобы на первой итерации получили ощутимое смещение все узлы карты. При этом в качестве расстояния d в формуле (2) предлагается использование сеточного расстояния d ² = ( i_BMU - i ) ² + ( j BMu - j ) ² .

Функция скорости обучения 5(n ) также представляет собой функцию, убывающую от времени. Наиболее часто используют линейную, обратно пропорциональную n

5 ( n ) = — const¹ —, или экспоненциальную n + const ₂

5( n ) = n ^{- 0.}2 .                                                                                   (4)

В работе [9] функции скорости обучения 5(n) и расстояния (латеральная связь [9]) h(d, n) модифи- цированы к виду

5 (n ) = n "°'2 •

^        ⁵⁽ n ^- n max ) ^

1 - e   n max

d ²

h (d, n ) = s r(n), где nmax – максимальное число итераций, s – константа близкая к нулю, d – евклидово расстояние ме- жду нейронами, r(n) – радиус обучения

r ( n ) = rmin +

^        ⁵⁽ n ^{- n} max ) ^

1 - e   ⁿmax

I J

( r max

I

n	>
s n max	- r min	- 0.25 • n
	J

здесь r _min, r _max – начальный и конечный радиусы обучения.

Как видно из приведенных функций, все они в большем или меньшем числе содержат параметры, результат подбора которых существенно влияет на качество построения адаптивной сетки, что означает высокую эвристику алгоритма.

Применение вышеописанного алгоритма, который назовем базовым, в сочетании с различными вариантами функции соседства приводит к трем основным проблемам:

• 1.    Адаптация сетки на невыпуклой области G не гарантирует, что все узлы сетки будут принадлежать области G .

• 2.    Граничные узлы построенной сетки расположены на определенном расстоянии до границы области, отличном от нуля. Это расстояние сопоставимо со средним расстоянием между узлами сетки.

• 3.    Нарушение гладкости адаптивной сетки вследствие уменьшения радиуса обучения на стадии уточнения.

• 0. Инициализация положений узлов сетки.

Для решения двух первых проблем в работе [7], которая посвящена использованию SOFM для построения конечно-элементных сеток, была предложена идея модификации алгоритма обучения SOFM, состоящая в том, что чередуется применение этого алгоритма отдельно для граничных и внутренних узлов. Один цикл такого чередования называется макроитерацией [8]. В соответствии с этой идеей был разработан модифицированный алгоритм построения конечно-разностных адаптивных сеток [9].

Модифицированный алгоритм.

• 1.    На первой макроитерации ( s = 1) применяется базовый алгоритм в течение n 0 итераций ко всем уз-

• лам сетки.

• 2.    На каждой макроитерации с номером s >  1 выполняются следующие действия:

• а)    применение базового алгоритма в течение n ₁ ( s ) итераций к граничным узлам сетки с генерацией точки только на границе области;

• б)    применение базового алгоритма в течение n ₂ ( s ) итераций ко всем узлам с генерацией точки во всей области. При этом все граничные узлы зафиксированы и не меняют своего положения. Кроме того, если узлом-победителем является граничный узел сетки, то он заменяет случайную точку x ( n ) .

• 3.    Повторяются макроитерации до тех пор, пока изменения положений узлов не станут достаточно малыми.

• 0. Устанавливаются начальные веса w_ij всех нейронов в вершинах квадратной решетки (рис. 1).

Идея решения третьей проблемы заключается в том, чтобы использовать граничные нейроны в качестве представителей несуществующих нейронов за пределами карты, которых не хватает для балансировки асимметричности латеральных связей. Алгоритм, осуществляющий сглаживание сетки, применяется после применения модифицированного алгоритма и выходит за рамки данного обзора.

Из приведенного обзора видно, что известный к настоящему времени модифицированный алгоритм адаптации сеток унаследовал эвристику базового алгоритма. Практика применения модифицированного метода указывает на необходимость наличия рекомендаций по выбору параметров обучения.

Вычисления и наблюдения

Вычислительные эксперименты проводились на симметричной невыпуклой области G (рис. 1). Выбор данной области G объясняется очевидностью правильного расположения сетки в первом шаге модифицированного алгоритма. В качестве функции соседства нейронов 0 ( n , i BMU , j BMU , i , j ) применялось произведение функции скорости обучения (4) и расстояния (2). Модифицированный алгоритм обучения программно реализован в виде следующих шагов.

• 1.    На первой макроитерации ( s = 1), соответствующей дискретному времени n е [1, n 0 ]:

  • 1.1.    Генерируется случайная точка x ( n ) во всей области G ;

  • 1.2.    Определяется нейрон-победитель в евклидовой метрике. Фиксируются сеточные координаты нейрона-победителя i_BMU , j_BMU ;

  • 1.3.    Настраиваются новые весовые значения нейронов сети по формуле (1)

_ ⁽ i BMU - i ) 2 ^{+ ( j}BMU - ^j ) 2

(п i j i i) = n^_°2-e    ^{2( a (} n ) n -“^

• n , _BMU , j_BMU , , j n e                   .

• 2.    На каждой макроитерации s >  1

  • 2.1.    В течение n 1 ( s ) итераций

    • 2.1.1.    Генерируется случайная точка x ( n ) на границе области G .

    • 2.1.2.    Определяется нейрон-победитель BMU из граничных узлов сетки.

    • 2.1.3.    Настраиваются новые весовые (5) значения граничных узлов сетки.

  • 2.2.    В течение n ₂ ( s ) итераций

    • 2.1.1.    Генерируется случайная точка x ( n ) во всей области G .

    • 2.1.2.    Определяется нейрон-победитель BMU среди всех узлов сетки.

    • 2.1.3.    Если в шаге 2.1.2 победил граничный нейрон сетки, то случайно сгенерированная точка x ( n ) заменяется на граничный нейрон.

    • 2.1.4.    Настраиваются новые весовые (5) значения внутренних узлов сетки.

• 3.    Повторяются макроитерации до тех пор, пока изменения положений узлов не станут достаточно малыми.

Первая макроитерация в классической терминологии соответствует этапу упорядочивания. Здесь важным показателем является правильность предварительного расположения сетки в области. Последующие макроитерации уточняют расположение сетки относительно границы и внутренней области G .

При анализе качества построения сетки в модифицированном алгоритме целесообразно разделить этапы упорядочивания и уточнения. В нижеследующих вычислительных экспериментах исследовались параметры a и n ₀ . За основу на первом этапе обучения принята линейная зависимость параметра a от дискретного времени n .

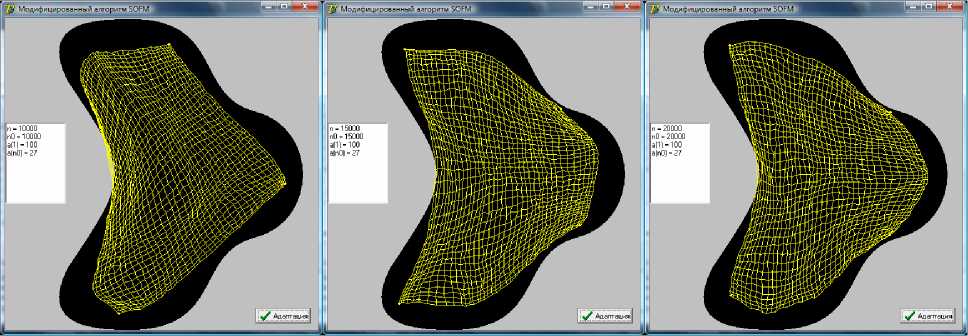
На рисунке 2 приведены итоги стадии упорядочивания в зависимости от числа итераций. Как видно, с увеличением числа итераций сеть, приспосабливаясь к особенностям области, на 20000 итерации приняла оптимальное положение. В части вогнутости области G некоторые нейроны вышли за края области.

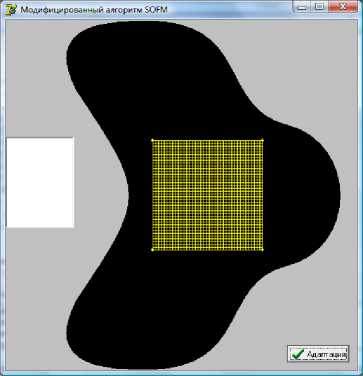
Рис.1. Область G с первоначальным расположением сетки в области адаптации

б)

a)

в)

Рис. 2. Предварительное расположение сетки в области при а ( 1 ) = 100, a ( n ₀) = 27 по истечении n ₀

итераций: а ) n ₀ = 10000 б ) n ₀ = 15000 и в ) n ₀ = 20000

б)

a)

в)

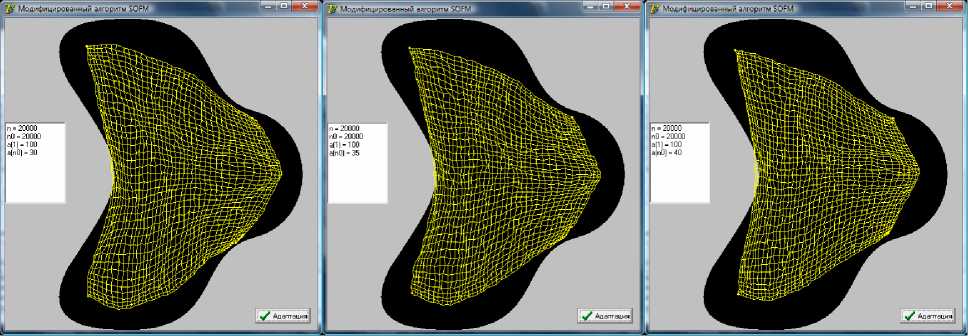
Рис. 3. Предварительное расположение сетки в области по истечении 20000 итераций для разных ва риантов нижнего предела параметра а: а) а(n0) = 30 б) а(n0) = 35 и в) а(n0) = 40

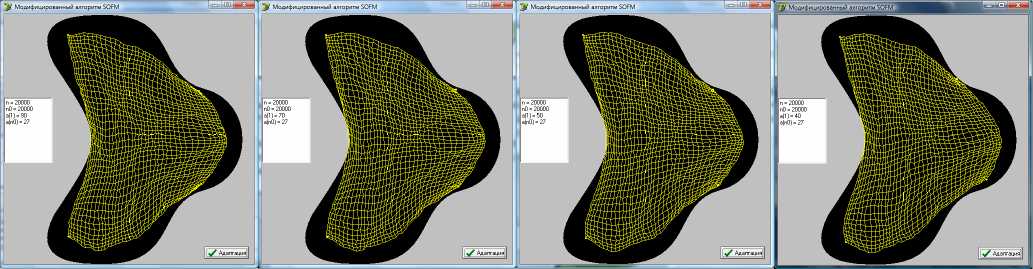
Увеличение нижнего предела параметра а при неизменных n 0 и a ( 1 ) приводит к ухудшению качества предварительного построения сетки (рис. 3). Это объясняется тем, что с увеличением нижнего предела радиуса обучения с т(п) (3) узлы сетки подвергаются большим смещениям на завершающей стадии и адаптационные свойства сети ухудшаются. Зависимость качества построения от верхнего предела параметра a при неизменных параметрах n ₀ и a ( n ₀) продемонстрирована на рисунке 4. Как видно, при уменьшении верхнего предела качество адаптации сетки также снижается (рис. 4 в ).

a)

б)

в)

г)

Рис. 4. Предварительное расположение сетки в области по истечении 20000 итераций для разных ва- риантов верхнего предела a : а) a (1) = 90 б) a (1) = 70, в) a (1) = 50, и г) a (1)- 40

Это обусловлено тем, что при большом радиусе начального обучения в первых итерациях сеть стягивается к случайно сгенерированным точкам, уменьшаясь в размерах. После чего медленно разворачивается, адаптируясь к особенностям области. При уменьшении начального радиуса сеть минует стадию «сжатия», и начальные размеры сети уменьшают возможности правильной адаптации.

Исследовался характер убывания параметра а от начального значения a ( 1 ) до a ( n ₀) (рис. 5). Вычислительные эксперименты с использованием экспоненциально убывающих функций показали (рис. 6), что характер убывания функции а ( n ) не вносит существенных отклонений в качестве построения предварительной сетки.

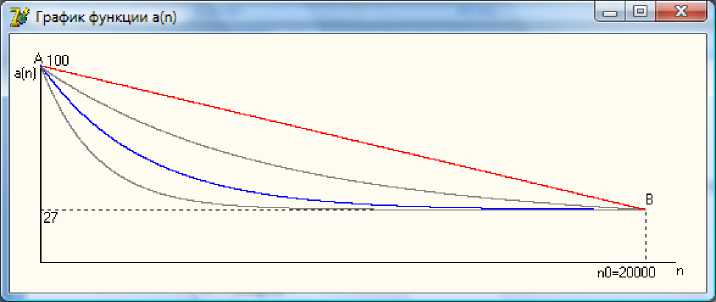
Рис. 5. Графики убывающих функций a ( n ) от точки A до B

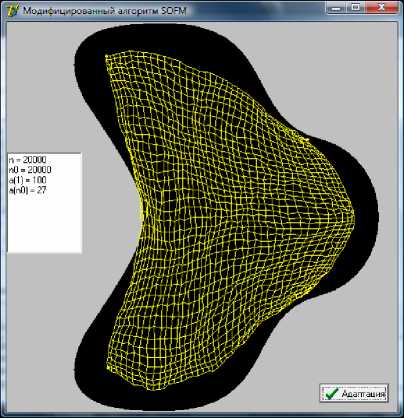
Рис. 6. Предварительное построение сетки для а ) экспоненциально убывающей функции a ( n ) б ) ли-

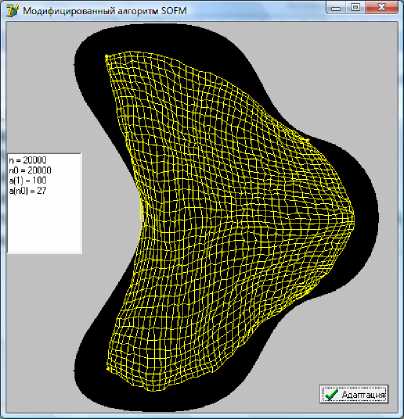
б)

нейно убывающей функции a ( n )

Таким образом, на стадии упорядочивания качество предварительного построения сетки обеспечивается правильным заданием точек A (1, a (1)) и B ( n ₀, a ( n ₀)) в плоскости построения функции a ( n ) . Функция a ( n ) может убывать линейно или экспоненциально.

На стадии уточнения эксперименты выявили целесообразность использования экспоненциально убывающей функции a ( n ) от B до некоторой точки C ( n _max, a ( n _max)) , расположенной достаточно близко к оси дискретного времени n . Использование линейно убывающей функции от B до C сохраняет качество адаптации, но значительно увеличивает время расчетов.

Пример построения адаптивной сетки для функции a ( n )

( a ( n ) - a (1) ,        .     , .

--( n ₀ - n ) + a ( 1 ) , при 1 < n <  n ₀

a (n) = <

n ₀

a(n0)• 1 - e I

⁵ ( n ^- n max ^- n 0 ) ^ n max ⁺ n 0

n - n 0

• ( 0.005 ) ⁿ max ^- n o + a _m in , при n 0 <  n <  n max

представлен на рис. 7. График функции a ( n ) изображен на рис. 8.

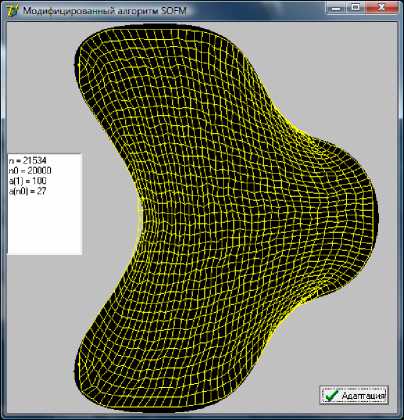
Рис. 7. Результат построения адаптивной сетки с применением (6)

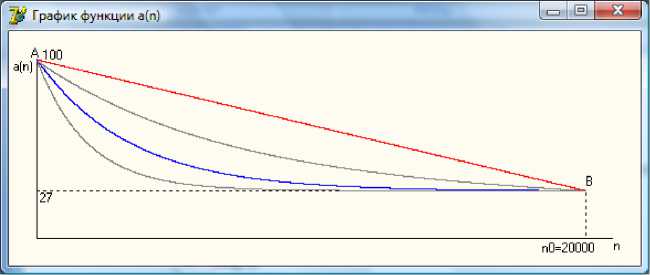
Рис. 8. График функции a ( n ) описанной соотношением (6)

Заключение

Существующие нейросетевые алгоритмы доказывают возможность построения адаптивных сеток на сложных физических областях. Результат адаптации сетки зависит от эвристики выбора параметров обучения нейросети. Для получения лучшего результата в модифицированном алгоритме SOFM целесообразно в качестве параметра a Гауссовой функции расстояния использовать линейно убывающую функцию на первой макроитерации и экспоненциально убывающую в последующих. Существенное влияние оказывает предварительное построение сетки, которое обеспечивается правильным заданием точек A (1, a (1)) и B ( n ₀, a ( n ₀)) в плоскости построения функции a ( n ) .