Модифицированные вейвлеты в обработке данных аналитических приборов. II. Алгоритмы обработки

В работе [1] рассмотрены вейвлеты, полученные модификацией известных ортонормирован-ных вейвлетных базисов (вейвлетов-"праро-дителей") { ф j , k ( t ) ^ , , k ( t ) ; j ^е Z , k ^е N } некоторой функцией G ( t ) . Новые базисные функции, обозначаемые как 6 _jk ( t ) , в _jk ( t ) — масштабирующие функции, n _jk ( t ) , П _jk ( t ) — вейвлетные функции, позволяют, в частности, вычислить оценку полезного сигнала x ( t ) , искаженного аппаратной функцией H ( t ) и шумом u ( t ) в наблюдаемом сигнале y ( t )

y ( t ) = j H ( t - т ) x ( т ) d T + u ( t ) .             (1)

Эта оценка имеет вид j ^

x(t)=Sc(kф^(t)+Ё Xdj(kКk(t),(2а) k                          j = j 0 k где j0 и J — самое тонкое и самое грубое значения масштаба соответственно. Показано, что получение оценки по формуле (2а) эквивалентно обработке наблюдаемого сигнала фильтром с частотным откликом G(to)

x ( to ) = G ( to ) y ( to )                  (2б)

и вейвлетным подавлением шума по алгоритму, предложенному в работе [3].

Коэффициенты вейвлет-разложения наблюдаемого сигнала y (t) — cj0 (k) и dj (k) определяются как cjo (k) = Jy (t)6Lo,k (t)dt’ dj (k) = !y (t)nJ,k (t)dt, где функции 6jk (t) и j)jk (t) должны удовлетворять следующим масштабирующим уравнениям:

6j,k (t) = X h (n - 2kвм,. (t),(4а)

n

ПJ, k ( t )=X g ( n - 2 k ) 6j+1,n ( t ) ,

n или

6j (t)=Xa)J+1 (n)фJ+1,n (t) ,

n

^7J (t) = X ^^j+1 (n)фу+1,и (t),

n где h и g — масштабирующие и вейвлетные коэффициенты вейвлетов-"прародителей", ос и /3 — масштабирующие и вейвлетные коэффициенты новых вейвлетов, которые определяются по формулам:

O^ j 41 ( n ) =

2^{J + 1} 2 п

2^{j + 1} n I - 2 ^{j + 1} n

Gd ( to ) hi ( 2 - ^{j - 1} to ) e ^{27 j - 1 to n} d to ,

Я + 1 ⁽ n ) =

1 2^{7+ 1} 2 n

2^{j + 1} n I - 2 ^{j + 1} n

Gi ( to ) g ( 2 - ^{j - 1} to ) e ^{27 j} - ^{1 to n} d to .

Обозначим aj+1 (to)= Gl(to)hi (2 j 1to),

(6а)

(6б)

(7а)

j ( to ) = G ( to ) g ( 2 -- Ю ) .             (76)

В настоящей части работы рассматриваются алгоритмы обработки наблюдаемых данных y ( t ) и приведены результаты их апробации на реальных сигналах аналитических приборов. Блок-схема алгоритма вейвлетной обработки наблюдаемого сигнала y ( t ) приведена на рис. 1. Наблюдаемый сигнал сначала подвергается дискретному вейвлетному преобразованию (ДВП), результатом которого являются коэффициенты вейвлет-раз-ложения c j ( к ) и dj ( к ) . При удачном выборе вейвлетного базиса энергия сигнала оказывается сосредоточенной в небольшом числе коэффициентов, в то время как энергия шума рассредоточивается практически по всем коэффициентам вейвлет-разложения. Благодаря этому обстоятельству в результате пороговой обработки (ПО) почти все коэффициенты шума приравниваются нулю и сохраняются только те коэффициенты сигнала, которые оказались выше порогового уровня. В блоке обратного ДВП (ОДВП) происходит восстановление оценки полезного сигнала, а в блоке оценки параметров (ОП) — расчет параметров сигнала, содержащих информацию об анализируемом веществе.

1. БЫСТРЫЕ ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ И БЛОКИ ФИЛЬТРОВ

Анализ

Чтобы получить быстрые алгоритмы для вычисления коэффициентов вейвлет-разложения оценки полезного сигнала X (t), подставим в (3 а, 3б) вместо в)к и fjjk их выражения из (4а) и (4б) соответственно. Получим:

c j ( ^к ) = ^ h ( ^{m - 2 к} ) ¹ j + i ( ^к ) ^{,             (8а)}

m

‘ё j ( ^к ) = Е g ( ^{m - 2 к} ) c j + i ( ^к ) •             ^(8б)

m

Так же как и в случае традиционного КМА, мы получили рекурсивный алгоритм для вычисления коэффициентов, который требует знания начальных значений c J ( к ) и d_J ( к ) на самом "тонком" масштабе J :

J ( ^к ) = ! y ( t ) ^в J , к ( t ) d t ,              ^(9а)

d J ( ^к ) = J y ( t ) ⁿ J , к ( t ) ^d t •             ^(9б)

Чтобы вычислить эти коэффициенты, так же как и в случае традиционного КМА, необходимо воспользоваться отсчетами наблюдаемого сигнала y ( t ) . Подставляя в (9а, 9б) выражения для в _jk и П_]к из (5а, 5б) и выполняя преобразования, получим

¹ J ( ^к ) = Е “ J + 1 ( m - ^{2 к} ) / y ( t ) ^ J + 1, m ( t ) ^d t ⁼

= ^ y ( m ) c j _{J + 1} ( m - 2 к )                (10а)

m

и

‘ё j ( ^к ) = X у ( ^m ) /^ j + i ( ^{m - 2 к} ) •               ^(10б)

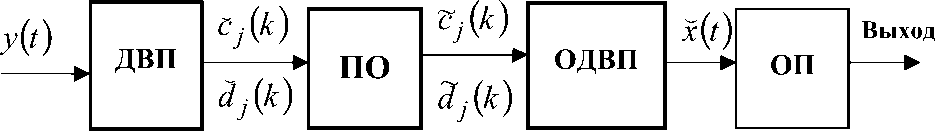
Рис. 1. Вейвлетное подавление шума. ДВП — дискретное вейвлетное преобразование; ПО — пороговая обработка; ОДВП — обратное ДВП; ОП — оценка параметров; y ( t ) — наблюдаемый сигнал; c j ( к ) , (1 j ( к ) — коэффициенты вейвлет-разложения наблюдаемого сигнала; c j ( к ) , d j ( к ) — коэффициенты вейвлет-разложения наблюдаемого сигнала после пороговой обработки; X ( t ) — оценка полезного сигнала

^a J + 1 ^(- n ) y ⁽ n ) ----------

^^

>^cJ - 1

h ( - n )

h ( - n )

^^

c J - 2

■„-

^C J - 3

h ( - n )

c o o + 1     ------------

c j o

^e J + 1 ( - n )

g (^- n )

g(-n)

g (^{- n} )

^^

d J - 1

^^

^d J - 2

^^

d J - 3

■™- d

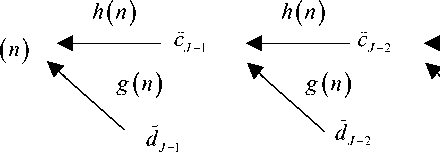
б

h ( n )

^^

---- Cj-3 .......... cj 0 +1 ^

( n)

dd,

UJ-3

Рис. 2. Схема 4-ступенчатого анализирующего (а) и синтезирующего (б) блоков фильтров. a J _{+ 1}, h и p j _{+ 1} , g — коэффициенты низкочастотного и высокочастотного фильтров вейвлетов

По формулам (8*) и (10*) можно построить вычислительную схему алгоритма анализа наблюдаемых данных, которая показана на рис. 2, а. В отличие от схемы [1, рис. 3, а] отсчеты наблюдаемого сигнала в первом каскаде подвергаются обработке низкочастотным и высокочастотным фильтрами с другими коэффициентами, а именно a J _{+ 1} и в J _{+ 1} соответственно. Коэффициенты фильтров на последующих ступенях анализа остаются прежними.

Синтез

Учитывая что U j _{+ 1} = U j © M j (см. [1, п. 3]), базисную функцию в j _{+ 1} k е U j _{+ 1} можно представить в виде

во+1, m (t ) =

= X вj+1, m ,в о, k ^j, k ( t )+ X вj+1, m ’П j, к )Пj, k ( t ) km или с учетом формул (26) и (29) в [1]:

во+1, m (t ) =

= X ^h ( m ^{- 2 k} ) ^e ~ , к ( t ) ⁺ X g ( ^{m - 2 k} ) ⁿ j , к ( t )• O¹) km

Умножая далее (11) скалярно слева и справа на y ( t ) , получим

C j + ( ^m ) =

= Xh (m - 2k)Cj (k) + Xg(m - 2k)dj (k).    (12)

km

Мы получили, таким образом, рекурсивную формулу восстановления коэффициентов вейвлет-разложения искомой оценки x ( t ) "от грубого к тонкому разрешению" с использованием, как и в анализе, фильтров-"прародителей" h и g . Вычислительная схема восстановления отсчетов оценки x ( t ) ничем не отличается от схемы традиционного КМА (ср. [1, рис. 3, б] и рис. 2, б).

Покажем теперь, что схема анализа—синтеза, показанная на рис 2, обеспечивает получение оценки полезного сигнала x ( t ) по наблюдаемому сигналу y ( t ), если значение масштаба J выбрано равным - 1, т. е. при J = - 1. Чтобы положить коэффициенты c ₀ ( k ) , равными отсчетам наблюдаемого сигнала y ( k ) , т. е. c ₀ ( k ) = y ( k ) , как уже отмечалось в [1], спектр масштабирующей функции ф ₀ ( to ) в пределах спектральной полосы y ( to )

должен быть максимально плоским. Это означает, что при использовании в качестве "прародителей" вейвлетов Добеши, имеющих плоскую частотную характеристику вплоть до частоты Найквиста, частота отсчетов наблюдаемого сигнала должна быть меньше п . Тогда из формулы (10) на первом шаге анализа необходимо выполнить:

с - 1 ( k ) = Х ^Й 0 ( m — 2 к ) У ( m ) ,           (12а)

m

■— d-1(к) = ^ во (m — 2к) У (m) •           (12б)

m

= G (го + п )х

■"

^^

х h(го)h(го + п) + exp(iп) h (го) h (го + п) = 0.

Первая сумма в квадратных скобках равна

^^

а0 (го)h(го) + в0 (го)h (го) =

= G(го)h(го)h(го) + G(го)h (го)h (го) =

= G(го) |h(го)|2 + h (го)|2 = 2G(го).

Рассмотрим работу первого каскада анализа и последнего каскада синтеза блока фильтров, который должен восстанавливать искомый сигнал в его дискретных точках X ( к ) (рис. 3). Можно показать [2], что вход и выход такого фильтра связаны выражением

X ( го ) = ¹

------------------                          .—- а0 (го)h(го) + в0 (го)h (го)

У ( го ) +

1 +—

^- а0 (го + п)h(го) + в0 (го + п)h (го)

у ( го + п ) .

Вторая сумма в квадратных скобках равна нулю, и, следовательно, равна нулю "элайзинговая" составляющая синтезируемого сигнала. Действительно, имеем с учетом (7*) при j = - 1

^^

а0 (го + п) h (го) + в0 (го + п) h (го) =

= G(го + п) h(го + п)h(го) +

+G (го + п) h1 (го + п) h1 (го) =

Следовательно,

X (го) = G (го)у (го).

Сравнение последнего выражения с формулой (2б) показывает, что применение вычислительной схемы рис. 2 для обработки наблюдаемых данных у ( t ) при соответствующем выборе G ( t ) приводит к желаемому результату получения оценки полезного сигнала X ( t ) .

• 2.    ОПИСАНИЕ АЛГОРИТМОВ

Таким образом, практическая реализация обработки данных с использованием модифицированных вейвлетов включает выполнение следующих этапов:

• а)    выбор или синтез функции G ( t ) в зависимости от круга задач решаемых прибором;

  

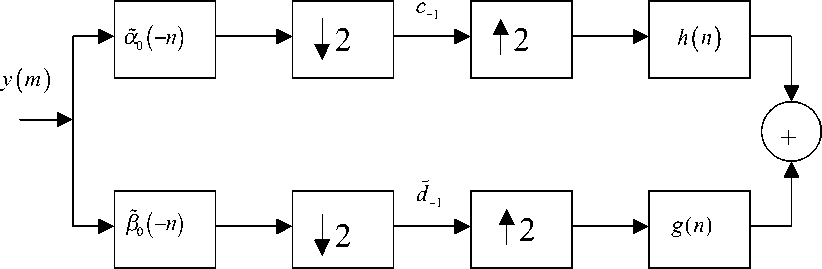
  Рис. 3. Первая ступень блока фильтров анализа-синтеза: у ( m ) — наблюдаемый сигнал; X ( m ) — оценка сигнала; 12 и $2 — прореживание и интерполяция с коэффициентом 2; с__х и d _х — коэффициенты анализа сигнала первой ступени

  
  

• б)    выбор вейвлета-"прародителя" (коэффициентов h ( n ) и g ( n ) );

• в)    вычисление коэффициентов а 0 ( n ) и в ₀ ( n ) ;

• г)    ДВП;

• д)    пороговая обработка вейвлет-коэффициен-тов;

• е)    ОДВП;

• ж)    оценивание параметров пиков.

Рассмотрим более подробно алгоритмы, реализуемые на каждом этапе обработки.

Выбор функции G ( t )

Деконволюция. Как уже отмечалось, выбор функции G ( ю ) , равной Й - 1 ( ю ) , приводит к большому уровню выходного шума. С целью подавления эффекта бесконечного усиления на практике применяют окна W ( ю ) или используют восстанавливающий фильтр Винера—Тихонова [4], регуляризирующий усиление на верхних частотах,

-/          Й (ю)

^G ( ю ) =         '           ^,              (14)

I Й ( ю ) + P R ( ю )

где в — регуляризирующий параметр, R ( ю ) — некоторый четный полином.

Выбирая константу в и полином R ( ю ) , можно легко корректировать ход частотной характеристики G ( ю ) .

Дифференцирование. Чтобы получить оценку p -й производной сигнала x ( t ) , искаженного прибором и шумами, функция G ( ю ) будет иметь вид

G ( ю ) = ( i ю ) ^p

Й ( ю )

IЙ (ю) |2 + в R (ю)

Если же необходимо получить оценку производной полезного сигнала без учета аппаратной функции, то можно воспользоваться дифференцирующими фильтрами Савицкого—Голэя [5]. Тогда функция G ( ю ) будет частотным откликом цифрового дифференцирующего фильтра, т. е.

G ( ю ) = G ( exp ( i ю ) ) = G 0 ( z ) , (16)

где z = exp ( i ю ) .

Интегрирование. При оценке текущего значе- t ния интеграла J x (т) dT с учетом искажений, t - T вносимых прибором и шумами, функция G (ю) будет иметь вид

G ( ю ) = ( i ю )

Й ( ю )

| Й (ю) |2 + в R (ю)

(Карунена—Лоэва)-подобные разложения (декорреляция). Известно, что разложение Кару-нена—Лоэва приводит к некоррелированным коэффициентам разложения [6]. Однако этот же результат можно получить с помощью предлагаемых вейвлетов. Предположим, что на входе системы Й ( ю ) действует белый шум с единичной дисперсией x ( t ) . Тогда на ее выходе он оказывается коррелированным с корреляционной функцией

K (т) = -П JK (ю) exp(i ют)dT , где K (ю) — спектральная плотность мощности и

K ( ю ) = | Й ( ю ) |2.

Выберем G ( ю ) = K ( ю ) ¹² и покажем, что коэффициенты разложения c j 0 ( k ) и dj ( k ) при этом будут некоррелированными. Действительно, с учетом (3а) получим

E [ Cv( m) Cv( k )] =

= JJ E [ y ( t ) y (^T )^{] Q} j , k ( t К k ( ^T ) ^d t ^{d T} =

= JJ ^K ( t ^{- T} ) ^Q i , k ( t ) ⁰' , , k ( ^T ) ^d t ^{d T} =

= 2П JK(ю)Q)j (ю)| exp(iю(m - n))dю =

= 2^ J ^ (ю) exp(?ю(m — n))dю = 8 (m - n), где символ E обозначает статистическое усреднение.

Аналогично можно показать, что

E [(7j (m)(7j (n)] = S (m - n).

Из формул [1, (19a, 21a)] при k = 0 можно получить интересный результат: ^^

K (ю)0,.(ю) = 0”(ю), или

JК (t - т ) Jt)dr = 0j( t), указывающий на связь масштабирующих функций модифицированных вейвлетов.

Однако так же, как в случае с деконволюцией, выбор G ( to ) = K ( to ) может оказаться некорректным вследствие слишком большого усиления на высоких частотах, поэтому G ( to ) необходимо строить по формуле (14), положив Й ( to ) = = K ( to ) ¹².

Коррекция частотной характеристики системы. Чтобы скорректировать частотную характеристику системы, необходимо умножить функцию G ( to ) на подходящий полином от частоты to . Например, чтобы поднять верхние частоты, достаточно умножить эту функцию на полином вида 1 + a 0 to ².

Выбор модифицируемых вейвлетов. Как было показано в [1], функции 6 , 6 , п , П порождают КМА, если в качестве модифицируемого выбран вейвлет с компактным носителем в частотной области (вейвлет Мейера или вейвлет Шеннона). Однако эти вейвлеты во временнóй области затухают очень медленно, определяются большим числом коэффициентов h и g и неудобны для приложений. Поэтому в качестве модифицируемых вейвлетов необходимо использовать другие вейвлеты, например Добеши высоких порядков, имеющих хорошую крутизну фронтов частотного спектра. Возникающая при этом систематическая ошибка может быть оценена численно в каждом конкретном случае.

Вычисление коэффициентов а ₀ и в ₀ • Эти коэффициенты определяются формулами (6а) и (6б) при j = - 1:

п

a0 (n) = — f G(to)h(to)eto ndto,         (18а)

2п -J в0 (n) = — J G(to)g(to)e'to ndto .         (18б)

^{2 п} -п

Для вычислений по этим формулам функции G (to), h(to) и g(to) должны быть определены на дискретном множестве (сетке) частоты to to = (N1: N, - 1)п/N,, где N1 выбирается в пределах 100÷200, что дает вполне удовлетворительный результат. Тогда ко- эффициенты a0 и в0 вычисляются по формуле обратного дискретного преобразования Фурье (ДПФ), которая для а0 имеет вид

1 N 1 ^{- 1}

« 0 ( ’ ) = ^ТГ 2 G ( m ) h ( m ) e " ² "  1 m =- N 1

для всех n = ( M 0 : M 1 ) , где M 0 и M 1 выбираются такими, чтобы a ₀ ( n ) = 0 при M 0 >  n >  M 1 .

По аналогичной формуле вычисляются коэффициенты в ₀ •

Если приборная функция Й ( t ) , которая в ряде задач определяет G ( t ) , задана на дискретной сетке t = ( - N 0 : N 0 ) , то ее ДПФ вычисляется по формуле

2 N о - 1

Й ( m ) = 2 H ( k ) e" ' ^п mkN 1

k = 0

для всех m = ( - N 1 : N 1 - 1 ) .

Если же функция G ( to ) определена по формуле (16) и так как h ( n ) и g ( n ) являются КИХ-фильтрами, коэффициенты а 0 ( n ) и в ₀ ( n ) могут быть получены путем умножения полиномов по степеням z :

« 0 ( z ) = ( ^G 0 * h ) ( z ) ,                ^(19а)

/^ 0 ( z ) = ( < G 0 * h 1 ) ( z ) .                  ^(19б)

Тогда искомые коэффициенты будут коэффициентами полиномов a 0 ( z ) и в ₀ ( z ) .

Быстрые дискретные вейвлетные преобразования (ДВП). ДВП имеют целью вычисление коэффициентов сj (k) и dj (k) для значений масштабов 0 > j > j0. Вычислительные процедуры и реализующие их блоки фильтров рассмотрены в [1, раздел 1] и здесь в разделе 1. Из формул (8*) и (10*) следует, что в основе структуры ДВП лежит блок фильтров, показанный в [1, рис. 4]. Их последовательное соединение по схеме рис. 2, а реализует процедуру анализа наблюдаемого сигнала y (t). В отличие от традиционного КМА, как показано на рис. 2, а, для достижения требуемого результата первый каскад блока фильтров должен быть снабжен коэффициентами фильтров ос0 (n) и в0 (n). Напомним, что операция децимации на каждом шаге анализа понижает число коэффициентов вдвое. Поэтому, чтобы достигнуть наиболь- шей глубины анализа по масштабу, выбирают число отсчетов наблюдаемого сигнала y (n) кратным степени двойки, т. е. N = 2J0. Тогда формально можно выполнить максимально J0 шагов анализа (J0 = log2 (N)), получив в результате N -1 коэффициентов dj и один коэффициент сj0. На практике часто применяют ДВП с избыточным числом коэффициентов (избыточное (redundant) ДВП), при котором иногда достигается лучшее подавление шума. В этом преобразовании в результате децимации коэффициенты не отбрасываются, а сохраняются. Тогда на первом шаге анализа получим пару векторов dj (k): dA (к) и dB (к) длиной N/2 каждый — и пару векторов сj (к): сА (к) и сB (к) длиной N/2 каждый. Векторы сА (к) и сB (к) на втором шаге подвергаются аналогичной обработке, в результате которой получаем четыре вектора dj (к) длиной N/4 каждый и четыре вектора сj (к) длиной N/4 каждый, и т. д.; выполнив J0 шагов, получим N log2 (N) коэффициентов d, и с, .

j j ₀

Программы, реализующие ДВП и избыточное ДВП, содержатся в последних версиях МАТЛАБ, а также их можно найти на различных сайтах ИНТЕРНЕТ, например [7].

Пороговая обработка коэффициентов вейв-лет-разложения. Пороговая обработка имеет целью удаление шума из наблюдаемых данных. Процедура пороговой обработки осуществляется только для коэффициентов d j ( к ) , которые сравниваются с порогом Tr , обнуляются, если этот коэффициент ниже порога, или сохраняют свое значение в противоположном случае. Очевидно, что идеальное удаление шума будет в том случае, если энергия сигнала в результате ДВП оказывается сосредоточенной в минимальном числе коэффициентов, а энергия шума размыта по максимальному их числу. Этого можно достичь в том случае, если базис будет хорошо коррелирован с сигналом, что и происходит для сигналов, имеющих небольшую продолжительность (для пиков), при применении вейвлетного базиса. Очевидно, что наибольшая корреляция будет в том случае, если масштабирующие и вейвлетные функции совпадают с формой сигнала.

Различают жесткую и мягкую пороговые обработки. Жесткая пороговая обработка строится по алгоритму [8]

d j ( к ) = -

d j ( ^к )

0,

если если

|dj ( к ) > Tr;

I d j ( ^к )^{s T} r.

а мягкая пороговая обработка:

	d j ( к ) - Tr j , если
d j ( к ) = -	d j ( к ) + Tr j , если 0,           если

I j ^к )k ^Tr j ;

I dj(к ^-T-j; I j к )< Trj, где порог для каждого значения масштаба j определяется как

Tr j = o j ^2ln N .                (20)

Дисперсия шума о2 определяется по формуле о2 = о2 S dL(n) , n

где d0, j — коэффициенты разложения функции G (t) по вейвлетным функциям d0j = = J G (t )nj, к (t)d t, о2 — дисперсия шума u (t). Эта дисперсия оценивается по наблюдаемым данным y (t) путем вычисления медианы коэффициентов dj (к) на самой тонкой шкале (j = 0). Если эта медиана равна Md, то оценка о будет o=

M d 0.6745

.

Обратные дискретные вейвлетные преобразования (ОДВП). ОДВП имеют целью восстановление дискретных значений оценки сигнала x ( n ) по коэффициентам вейвлет-разложения наблюдаемого сигнала y ( t ) , прошедшим пороговую обработку. Вычислительная схема ОДВП показана на рис. 2, б.

Оценка параметров пиков. Параметрами пиков, содержащими информацию об анализируемом веществе, являются их амплитуда, положение максимума (или центра тяжести) и площадь. Для определения этих параметров обработке подвергаются отсчеты x (n), которые являются случайными величинами, подчиняющимися, как правило, закону нормального распределения. Чтобы оценить перечисленные выше параметры пика, нужно прежде всего его обнаружить. Для этого используются такие критерии, как интенсивность отсчетов x (n), крутизна фронтов и ширина пика. Все эти показатели вычисляются в текущем окне данных из трех и более отсчетов и сравниваются с эмпирически выбранными порогами. Площадь определяется как сумма отсчетов в пределах от начала до конца пика, интенсивность — как величина максимального отсчета в этих же пределах, а положение пика — как положение максимума. Для более точного определения параметров отсчеты в окне данных могут быть аппроксимированы, например, квадратичным сплайном.

• 3.    ПРИМЕРЫ ПРИМЕНЕНИЙ

В практике предварительной обработки сигналов решаются задачи оценки функции x ( t ) , ее p -й производной или текущего значения интеграла

t

J x(т)dT при условии минимизации величины t - т соответствующего среднеквадратического отклонения (СКО):

II ^x ( t )^{- x} ( t )|| <  ^e 0 ,

I ^{x ( p )(} t )^{- x (} t ^{)( p} ) ll< ^e p ,

J x(т)dT - J x(т)dT t - T                 t - T

T ^,

где e * >  0 — некоторая заданная ошибка.

Чаще всего используют относительное СКО, определяемое как

RMSE( x - x) = { e У J x ( t )| 2 d t } ².          (23)

а                                                б

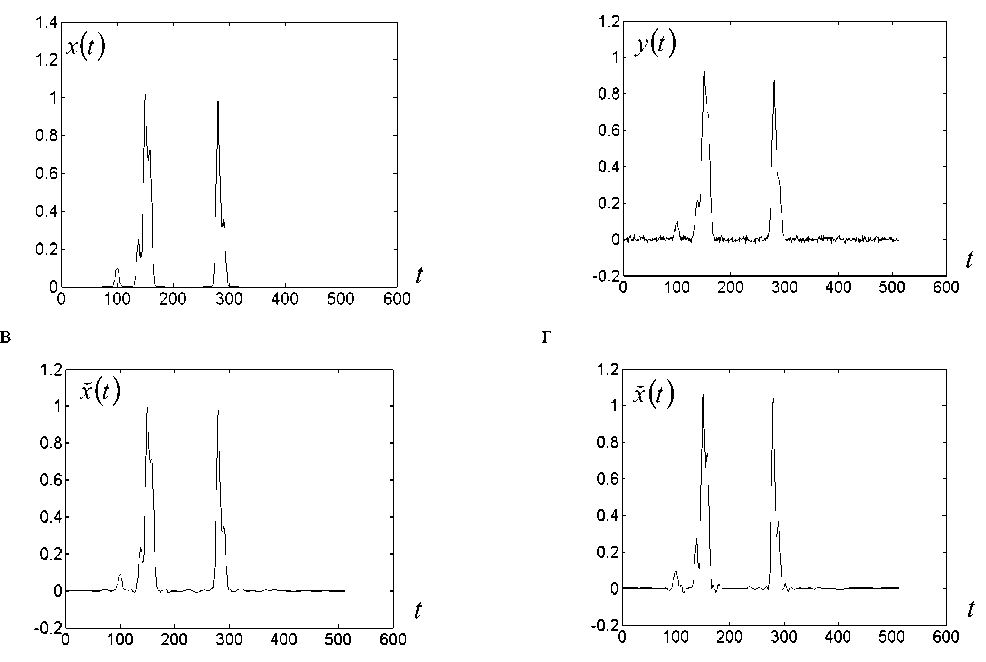
Рис. 4. Пример деконволюции модельного сигнала.

а — оригинальный сигнал x ( t ) ; б — наблюдаемый сигнал y ( t ) с шумом при отношении сиг-нал/шум 10 (RMSE ( x - у ) = 0.1); в — оценка сигнала x ( t ) с шумом (RMSE ( x - x ) = 0.03, в = 0.02, 7 ? ( to ) = 1); г — то же, что и (в), но с усилением верхних частот с помощью полинома 1 + to ²

а

2000    200   400   600   800 1 000 1 200

t

б

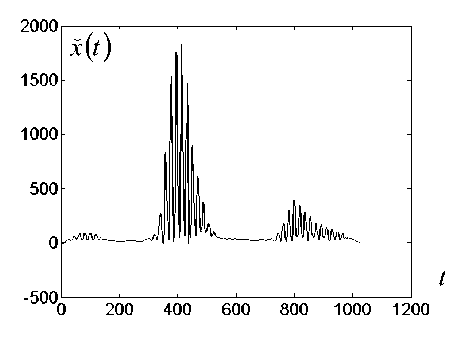
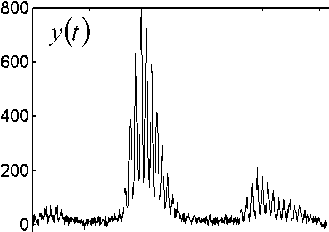
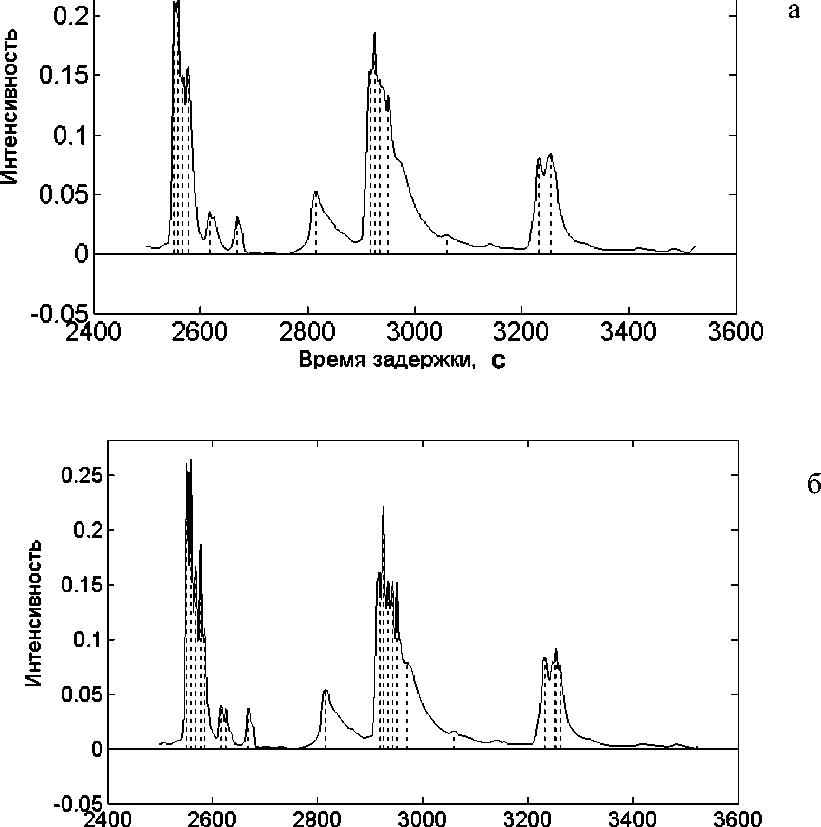
Рис. 5. Фрагмент спектра инсулина времяпролетного масс-спектрометра.

а — наблюдаемый сигнал, б — оценка сигнала, полученная методом обратной свертки

В дальнейшем будем пользоваться величиной относительного СКО, чтобы оценить степень зашумленности сигналов, качество подавления шума, качество полученной оценки и т. п. Отношение сигнал/шум в приведенных ниже примерах будем оценивать как отношение амплитуды компонента сигнала самой минимальной интенсивности к среднеквадратическому значению шума.

Деконволюция. Применим сначала предложенный подход для решения задачи деконволюции. Задача деконволюции является некорректной, т. к. не существует физически реализуемых способов точного восстановления искаженного линей-

ной системой сигнала. Приближенное решение задачи возможно путем применения функции G ( to ) , заданной формулой (14). Выберем модельный сигнал с белым шумом, определенный на множестве точек N = 2 9 , состоящий из шести пиков га-

уссовой формы a_k exp

⁽ t ^- t k )

² ^ 0

, где

a_k = [ 0.1 0.251.0 0.71.0 0.35 ] ,

t k = [ 100138150159 280 290 ] , ц ₀ = 3.2.

Приборная функция принята равной

H (t ) = exp -

t ²

2 ^ 02 J

, R ( to ) ^ 1, и коэффициенты

a ₀ ( n ) и в ₀ ( n ) определялись по формулам (18*).

Результаты приведены на рис. 4. Как следует из рис. 4, г, определенный положительный эффект дает усиление верхних частот умножением G ( to ) на полином 1 + to ².

На рис. 5–8 приведены примеры обработки реальных сигналов времяпролетного масс-спектрометра, спектрометра Мессбауэра, электронного спектрометра и секвенатора НАНОФОР 3. Приборные функции в первых двух случаях определялись по форме одиночного пика этих приборов, во втором и третьем случаях выбиралась в виде гауссовой кривой. Фильтр G ( to ) строился аналогично предыдущему примеру.

Дифференцирование. Операция дифференцирования применяется в тех случаях, когда необходимо оценить, например, скорость или ускорение движения, выделить изменения, происходящие в наблюдаемом сигнале, локализовать скачки в уровне сигнала и оценить их величину и др. Дифференцирование в присутствии шумов приводит к значительному увеличению их интенсивности и снижению отношения сигнал/шум, особенно при вычислении производных второго и более высоких порядков. Предлагаемый метод, совмещающий операцию дифференцирования и вейвлетного подавления шума, позволяет в несколько раз уменьшить влияние шума на оценку производной.

Сравним этот метод с существующим, например использующим дифференцирующие фильтры второго порядка Савицкого—Голэя (СГ) [5], на модельном сигнале рис. 4, а (см. рис. 9).

аб

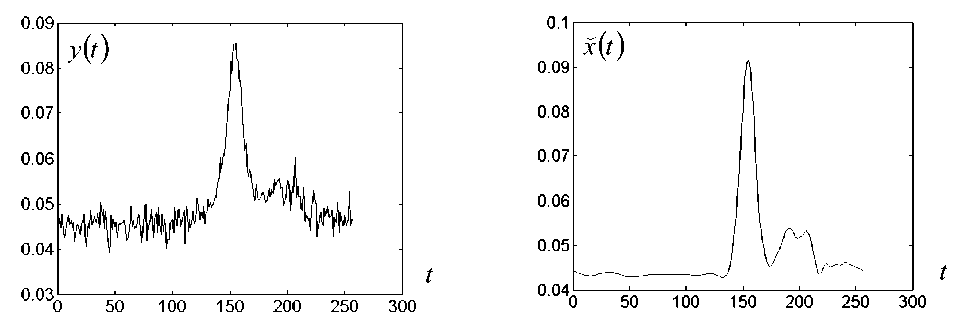
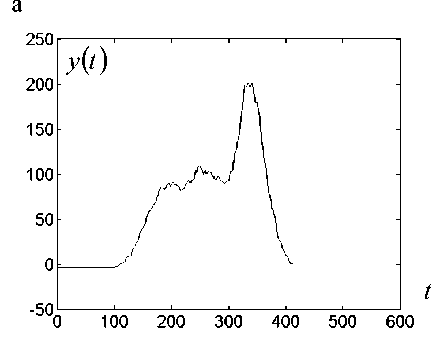
Рис. 7. Фотоэлектронный спектр.

а — наблюдаемый сигнал; б — оценка сигнала, полученная методом обратной свертки с усилением верхних частот с помощью полинома 1 + 150 ®²

Рис. 6. Мессбауэровский спектр продуктов реакции образования SnS (олово—сера).

а — наблюдаемый сигнал; б — оценка сигнала, полученная методом обратной свертки с усилением верхних частот с помощью полинома 1 + 10 ®²

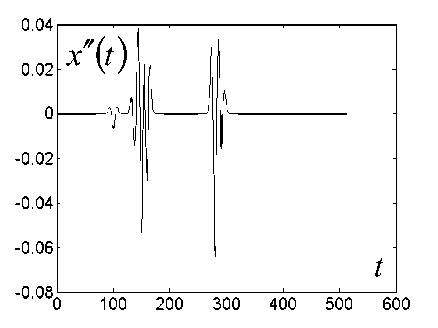
Ошибка дифференцирования определялась по величине СКО от истинного значения производной x" , вычисленной по известным правилам дифференцирования. Если при отсутствии шума (рис. 9, б) этой ошибкой можно пренебречь (RMSE ( x' - x") = = 10 ^{- 12}), то в присутствии шума (рис. 9, в) метод СГ приводит к величине СКО ~28 %. Более того, производная от пика минимальной интенсивности (первый пик) оказалась полностью скрытой в шумах. Предлагаемый метод (рис. 9, г) приводит к величине СКО, равной ~8 %, и к четкому выделению производной минимального пика на фоне шумов.

Вычисление коэффициентов a ₀ ( n ) и в ₀ ( n )

в этом случае производилось по формулам (19*).

(Карунена—Лоэва)-подобные разложения (декорреляция). В формуле (14) положим R ( ® ) = = 1 и в = 3-5 • 10 - 8 . В качестве модельного сигнала x ( t ) выберем белый гауссовский шум, N = 2¹⁰ и фильтр

H ( ® ) =

1 + у ® ®

при y 2 = 10.

Тогда случайный процесс на выходе фильтра будет описываться экспоненциальной корреляцион- ной функцией K (т ) = exp - т

Y

Коэффициенты

а ₀ ( n ) и в ₀ ( n ) вычисляются по формулам (19*).

Результаты обработки приведены на рис. 10.

с

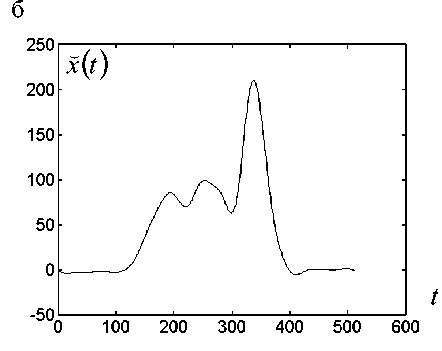
Рис. 8. Фрагмент сигнала ДНК, полученного на приборе НАНОФОР 3.

а — наблюдаемый сигнал; б — оценка сигнала, полученная методом обратной свертки

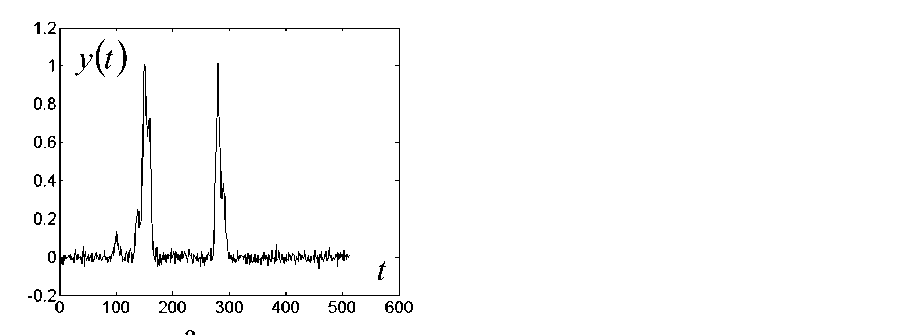
б

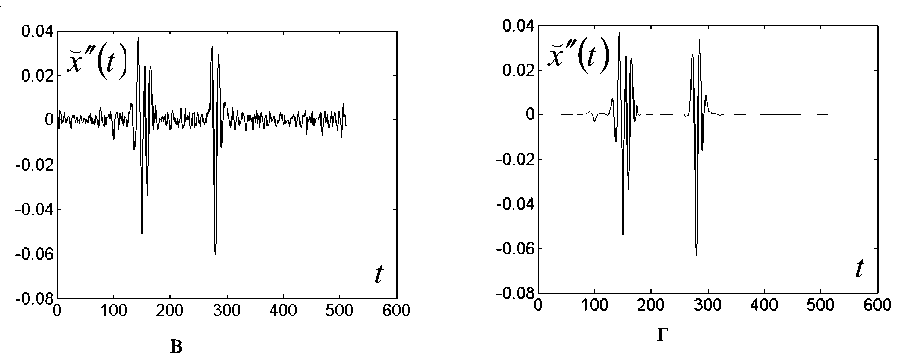
Рис. 9. Пример вычисления второй производной модельного сигнала с использованием девятиточечного третьего порядка фильтра Савицкого—Голэя.

а — наблюдаемый сигнал у ( t ) с шумом при отношении сигнал/шум 5 (RMSE ( x - у ) = 0.1); б — оценка второй производной без шума (RMSE ( x" - x") = 2 - 10 ^|2, в = 0.004, 7 ? ( ю ) = 1); в — оценка второй производной без подавления шума (RMSE ( x" - x" ) = 0.28, в = 0.04, R ?( ю ) = 1); г — оценка второй производной с подавлением шума (RMSE ( x "- x" ) = 0.087, в = 0.04, R ( ю ) = 1)

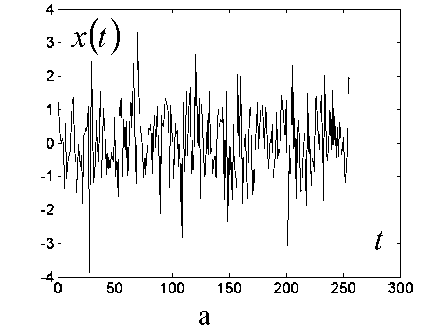
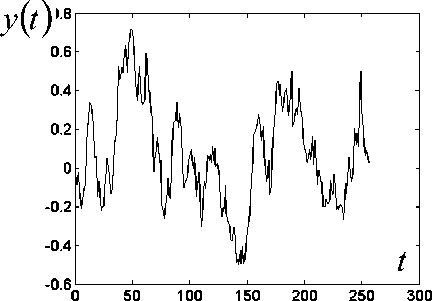
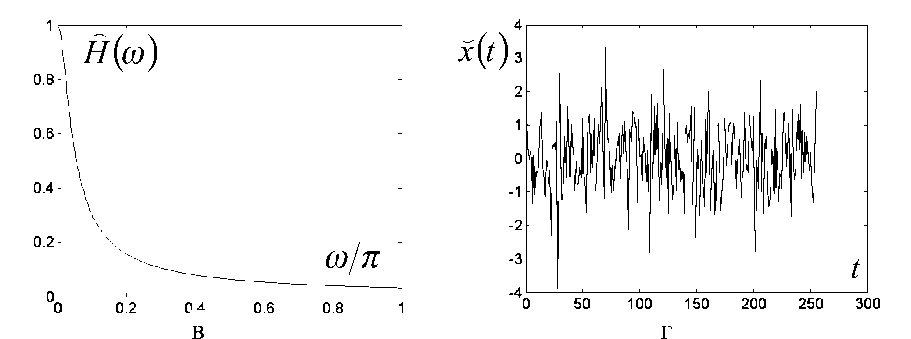
Рис. 10. Декорреляция (отбеливание) шума.

а — фрагмент тест-сигнала ( N= 1024); б — наблюдаемый сигнал y ( t ) , в — частотная харак

теристика системы н ( ю ) =

71 + у ю ²

; г — декоррелированный сигнал (RMSE( x-x)= 0.028)