Модифицированный масс-рефлектрон

Известно, какую выдающуюся роль в развитии времяпролетной масс-спектрометрии сыграла идея масс-рефлектрона [1]. Классическая его схема, состоящая из дрейфовой трубки и плоского электростатического зеркала, уже обеспечила энергетическую фокусировку первого порядка для полных пакетов. Желание улучшить качество фокусировки породило схему с двойным зеркалом из двух плоских конденсаторов, вплотную следующих друг за другом [2]. Здесь удается получить фокусировку второго порядка, и масс-спектрометр становится весьма совершенным. Этот успех естественно порождает мысль использовать тройные, четверные и т. д. зеркала для получения любого заданного нами порядка фокусировки. Иллюзии однако разбиваются рассеивающим и затеняющим действием сеток, разделяющих секции зеркала, сводящим на нет все теоретические преимущества многоэлектродных систем. Именно поэтому на практике доминирует схема с двойным зеркалом как своеобразный оптимум [3].

Тем не менее мы решаемся предложить новый вариант схемы, идейно прилегающий к первоначальной; мы назвали его "модифицированный масс-рефлектрон" [4]. Несмотря на то что эта область как будто бы исхожена вдоль и поперек, мы неожиданно наталкиваемся на принципиально новые и технологически приемлемые решения.

ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ

Рассмотрим сначала масс-рефлектрон в его первоначальной классической форме: заземленная дрейфовая трубка длины H снабжена на конце отражающим плоским зеркалом с потенциалом Ф 0

и зазором l между пластиной и сеткой (рис. 1). Ион массы m и зарядом q стартует из источника I в момент t ₀ = 0 с энергией E и пролетает двойной путь до детектора D за время t D , которое мы представим в виде

t D = н 2mKк ( e ),            (1)

где

к =  + ^ E , Ц = -2—

E           2 Ф ₀ H

.

Графики функции K ( Е ) суть ямы с крутыми левыми берегами при E ^ 0 и перегибистым пологим правым берегом при E ^^ (рис. 2). На дне

dK ямы — = 0, в чем, собственно, и состоит факт dE

достаточно хорошей фокусировки по энергии для группы ионов с размазанной энергией E . Величина min K характеризует полное время пролета в условиях фокусировки и вместе с аберрацией второго

d² K порядка, пропорциональной , d E ²

задает разре-

шающую способность прибора.

Если где-нибудь в дрейфовую трубку встроить электронно-оптический элемент со сквозным про-

ходом: линзу, конденсатор, — то независимо от природы его действия (тормозит он или ускоряет) к функции K добавится аддитивный положительный член, всегда имеющий вид падающей с ростом Е функции. При этом дно ямы (2) всегда поднимается, а плато возле дна деформируется и может приобрести вид достаточно протяженной площадки при большой вариации Δ Е . Именно к "пологости" дна и должен стремиться конструктор прибора.

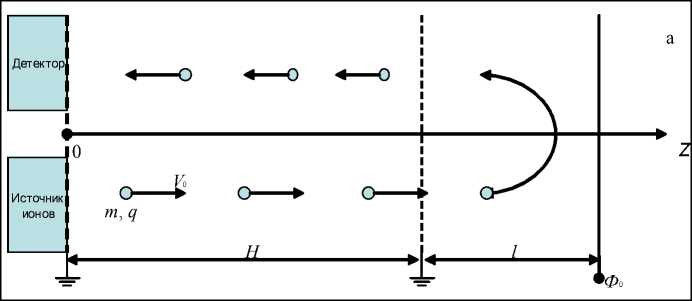
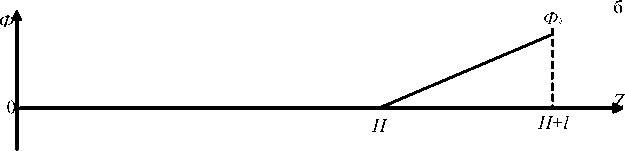
Рис. 1. Масс-рефлектрон (а) и профиль потенциала в нем (б)

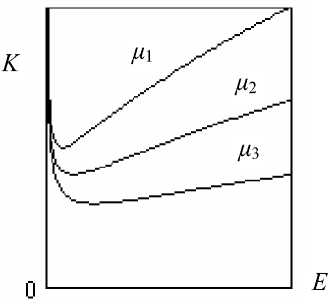
Рис. 2. Функция K ( Е ) при различных µ

Итак, мы будем стараться простыми средствами деформировать яму (2), выбирая подходящую полевую структуру.

Как известно, локальная форма кривых характеризуется рядом Тейлора с центром разложения в выбранной точке. Мера близости кривой в окрестности центра разложения к горизонтальной прямой характеризуется величиной соответствующих коэффициентов Тейлора. В случае обнуления коэффициентов до какого-либо порядка n мы имеем фрагмент кривой тем ближе к горизонтальной, чем выше этот порядок n. При этом говорят о фокусировке n-го порядка. Поэтому, желая освободиться от влияния разброса энергии на время пролета ионного пакета, мы должны стремиться к уничтожению как можно большего числа производных в ряде Тейлора.

Логика нашего рассуждения требует взять в качестве достойного преобразователя систему, проще которой не бывает, а именно двойной электрический слой со скачком потенциала Ф 1 , и расположить его на расстоянии h от старта параллельно зеркалу (рис. 3, а). Входную сетку зеркала запитаем потенциалом Ф 1 , а его второй электрод потенциалом Ф 2 . Все эти величины еще подлежат определению. Ход потенциала вдоль оптического пути имеет форму, как на рис. 3, б. Таким образом, ион летит с постоянной скоростью отрезок h , далее скачком меняет энергию на величину Q 1 = = qФ 1 , причем в зависимости от знака Ф 1 либо тормозится ( Ф ₁ > 0), либо ускоряется ( Ф ₁ < 0), и отрезок ( H–h ) до зеркала летит с другой дрейфовой скоростью. Далее ион отражается от зеркала и совершает свой путь до детектора D в обратном порядке. В результате система приобретает новые и несколько неожиданные свойства. Мы исследуем все это, двигаясь от простого к сложному, и начнем с идеальной схемы с бесконечно тонким двойным слоем.

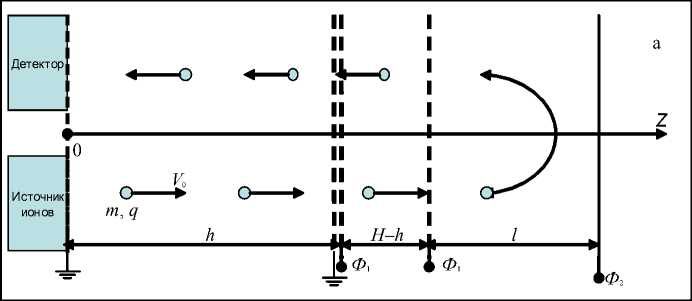
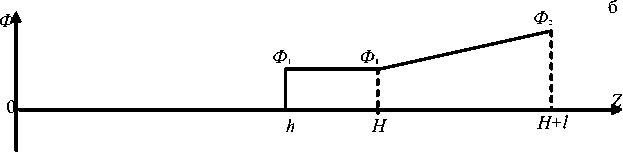
Рис. 3. Идеальный модифицированный масс-рефлектрон (а) и профиль потенциала в нем (б)

ИДЕАЛЬНЫЙ ВАРИАНТ

Пусть двойной слой будет тормозящим ( Q 1 > 0). Составим выражение для полного времени пролета:

mm tn — 2 h     + 2( H — h)--+

D 2E E           ^/2( E — Q 1 )

+ 2l- 4 2 m ( E — Q J,

Q ₂

d K   d² K

Вычислим и ₂ и приравняем их к нулю. d w   d w ²

Получим линейную алгебраическую систему относительно величин в и Y , дающую условия фокусировки второго порядка ионных пакетов по энергии Е . В приведенной форме она такова:

где

Q 2 — q ф — ф ),   Q i — q Ф 1 .             (4)

Для удобства выкладок преобразуем (3) к виду tD — h mK(w),             (5)

Q ₁

где к—+в Ww^+ + Y—,       (6)

V w          Ww — 1

Ее корни:

( w — 1) в — Y —

( w — 1) в — 3 Y —

3( w — 1)¹²

^в          5/    ’

2 w ²

3 w — 1 А ²

I ,

w )

5 w — 1 А ²

.

w

( w — 1) 32 (3 — 2 w )

^Y              5/

2 w ²

.

E     lQ w — —, в — 2--L,

Q 1        hQ 2

Y —

H — h h

По физическому смыслу система может работать только в том случае, если E >  Q 1 , т. е. w >  1. С другой стороны, из геометрии в (7) всегда у >  1, но тогда выражение (9) обязано быть положительным. Следовательно, интервал w , в котором достигается фокусировка второго порядка по w (а соответственно и по Е ) определяется неравенством

разрешающей способности, которая с помощью соотношений (5) и (6) примет вид

Вычислим теперь с помощью (6):

d³ K производные , d w ³

d⁴ K d w ⁴

A m _ 2 A t_D _ 2 A K mt_D  K

По формуле Тейлора A K в условиях фокусировки имеет представление:

d³ K _ 3

d w ³   8

d⁴ K _ 15

d w ⁴ 16

7 w ²

5Y

( w -1/²  ( w -1/²

,

A K = -d- K ( A w ) 4 .               (20)

4! d w ^{4 (} )

9 w ²

7Y

( w - 1/²  ( w - 1/²

.

Соединяя (17, 18, 20) в выражение (16), получим

Далее, подставив в (11), (12) и (6) значения в из условий фокусировки второго порядка (9) лучим выражения:

d³ K _ 3 ( 4 w - 5 )

d w³   8_W%A -- A²’

d⁴ K _ 5 - 12 w² + 21 w - 7 d w⁴ 16 _w92f₁ -- 1? ,

4 w - 3

K ^_ —5

w ²

.

Первое, что бросается в глаза, — это обраще-d3K ние в ноль производной при dw3

окончательно и у

, по-

	A m 4     4 ---= —(A w ) . m 5	(21)
Но	E w _ — Q 1	(22)
и	a   A E A w _ . Q 1	(23)
Из (22)	и (16) получаем
	Q i _ 4 E - 15	(24)
Подставляя Q 1 из (24) в (23), получим

w _ — .

Это значение попадает в физически допустимый интервал (10), и, следовательно, в системе осуществляется фокусировка третьего порядка. Факт замечательный, если учесть, как скромно мы вмешались в дрейфовое движение при помощи тормозящего двойного слоя.

Вычислим (14, 15) при энергии фокусировки (16). Получим

	5 A E A w _-- . 4 E	(25)
Подставим A w	из (25) в (21) и	запишем формулу
разрешающей	способности	нового масс-
рефлектрона:	A m _ 125 ( A E m "  64 I e	4 I -                 (26)

d⁴ K    _ 3 • 2¹⁰

d w⁴ w _ 5 " 12575 ^, w ₂

K 5 _--- r

¹ w ^_ 2 2575

Из (24) следует, что на тормозящем двойном слое должно гаситься ⁴ ₅ от первоначальной энергии Е . Если принять, что в зеркале ионы поворачивают назад непосредственно у второй пластины с потенциалом Ф ₂, то надо положить

Этих данных уже достаточно, чтобы оценить разрешающую способность построенной схемы масс-рефлектрона в режиме фокусировки третьего порядка. Воспользуемся стандартной формулой для

qФ 2 _ E -                    (27)

Тогда

Q 2 _ qФ 2 - qФ 1 _ 5.               (28)

Вычислим еще в, у в режиме фокусировки третьего порядка, положив в (9) w = 4. Получим в = -24= у = 1

25 5      25 5

Соединяя эти значения с формулами (4) для в , Y и используя Q1 из (28), мы можем записать уравнения, в которые входят неизвестные пока величины h и l. Разрешив их, мы получим l = -^ h = 0.054h,

25 5

H - h =      h = 0.0179 h.

25 5

В классическом масс-рефлектроне с одинарным зеркалом расстояние между пластинами составляет 50 % от длины дрейфовой трубки. В нашем случае двойной слой, дрейфовая промежуточная часть ( H – h ) и размах зеркала l вместе составляют всего 7.2 % от длины h , что весьма удобно с тех-нологически-конструкторской точки зрения. Физическое время пролета в новой системе при одинаковых габаритах с классическим масс-рефлектроном увеличивается примерно в 1.5 раза, что также имеет большое значение при реализации прибора.

Итак, мы подробно изучили теоретическую схему модифицированного масс-рефлектрона с идеальным торможением на двойном электрическом слое. Оценим его разрешающую способ ность, взяв AE = 2.5 эВ. Тогда из (26) получим

— = — f) = 0.76 -10-6 m 64 I 40 I или разрешение R

R = m- = 1.3 - 10 6 .

A m

Сила прибора очень значительная!

РЕАЛЬНЫЙ ВАРИАНТ

Двойной электрический слой в наших предыдущих построениях может восприниматься как математическая абстракция, сомнительная для технической конструкции. Поэтому мы обязаны заменить этот бесконечно тонкий слой более ощутимым толстеньким плоским конденсатором с зазором S между сетками и провести новое, более сложное исследование системы (рис. 4, а). Ход потенциала вдоль оптической оси системы становится более гладким (рис. 4, б); появляется новый участок с тормозящим полем длины S .

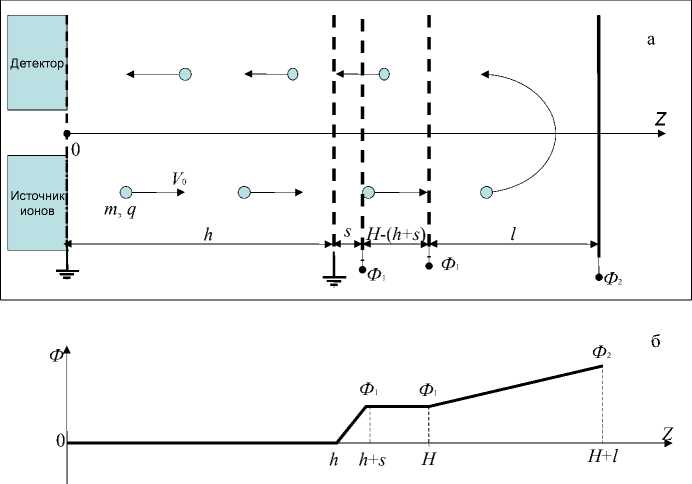
Рис. 4. Реальный модифицированный масс-рефлектрон (а) и профиль потенциала в нем (б)

Составим общее выражение для полного времени пролета t_D по тем же правилам и с теми же обозначениями параметров и запишем:

t_D = h —K ( w ),

^{D        Q} 1        ^,

где K по сравнению с (6) несколько усложнится и появится новый коэффициент а , причем изменится и содержание величин а , в и у :

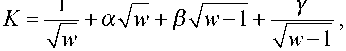
Система (36) переходит в новую рациональную систему относительно ^ , п и X :

w 2 ^ + ( w - 1)² п - ( w - 1)² X = w ²,

- w c + ( w - 1) п - 3( w - 1) X = 3 w ,         (39)

£ + п + 5 X = 5.

Определители этой системы вычисляются очень просто. Мы опустим короткие элементарные выкладки и сразу же запишем решение:

„ г л        4 w ² + w . w

£ = 5 - 4 w , п =-----—, X =---- .     (40)

w - 1         w - 1

в = 2 ^{lQ 1} - 2 - , hQ ₂ h

Из (38) с помощью (40) находим значения а , в и y , отвечающие условиям третьего порядка, аберрационный член (37) и, наконец, K по формуле (34). Имеем:

а, в и у можно считать независимыми параметрами, подлежащими определению из дополнительных условий. Здесь естественно попытаться выявить фокусировку третьего порядка, вычислив dK d2K    d3K производные , и и приравняв их dw dw2d к нулю. Получится система алгебраических уравнений относительно а, в и у, которая приводится к виду а + в

Vw  Vw - 1 (w -1)32

OL^^{Y 3}

3/ +         3/3         5/5/ w22   (w -1)/2    (w -1)/2

а + в - 5 Y= _5_ w 52 (w -1)52    (w -1)% w72

Если эти уравнения удовлетворяются, то остаточный член в выражении AK определится величиной d4K = 15 Г_7_ d w   16 w 92

а в       7 Y

7/     , х7/ + , х9/ wл  (w -1)/2 (w -1)/2

Решение (36) в приведенном виде представляет довольно-таки громоздкую и малопрозрачную процедуру. Мы чрезвычайно сократим вычисления, если введем следующие искусственные подстановки:

5 - 4 w _о ( w - 1 ) ²²

а =------, в =   5т— (4 w +1), w           w 2(41)

( w - 1 А²²

Y = 1I

V w J

' d4K=_JJ___ dw4 8w92 (w -1)2

IK = 4

L w ^{2 2}

Теперь у нас нет дополнительного условия на w , как в случае идеального двойного слоя, и фокусировка третьего порядка может осуществляться при некоторых энергиях, если подобрать нужным образом параметр тормозящего слоя S . Сопоставляя а из (35) и (41) мы видим, что а >  0, и кроме этого, всегда должно быть w >  1, так что w оказывается заключенным в интервале

1 <  w <  4.

Учтя все эти новые обстоятельства, вычислим разрешающую способность:

A m _ 2 A K = 5   ( A w ) 4

m ” 64 w ² ( w - 1 ) 2 .

Эта величина достигает минимума, если w достигает максимума, что в силу неравенства (43) дает w = 4. С другой стороны,

w

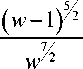
Y =

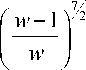
X .

2 S  5 - 4 w а = V =----, hw

и при w = 4 формула (44) переходит в (21), так что неизбежно следует вывод:

в условиях фокусировки третьего порядка наилучшим является вариант с идеальным двойным слоем ( S = 0) в качестве притормаживающего устройства.

На практике S надо выбирать на пределе технологических возможностей. С помощью выражений (35) можно определить (уточнить) параметры конструкции, взяв приемлемо малую толщину S , регламентируемую, например, пробойным напряжением и рассеянием на сетках. Здесь мы этими расчетами заниматься не будем.

ТРЕХСЕКЦИОННОЕ ЗЕРКАЛО

Комбинация узкого тормозящего слоя, следующего за ним потенциального дрейфового промежутка и последнего отражающего каскада на самом деле является частным и даже вырожденным случаем трехсекционного зеркала с зазорами l1, l2, l3 и потенциалами 0, Ф1, Ф2, Ф3 (рис. 5, а). Все предыдущее отвечало условию Ф1 = Ф2. Мы вправе предположить, что появление еще одного дополнительного варьируемого параметра должно изменить всю ситуацию с фокусировкой по энер- гии, и, в частности, может возникнуть фактор уменьшения аберрации четвертого порядка. Ответить на этот вопрос может только точный математический анализ, хотя здесь он будет более длинным.

Рассмотрим только режим торможения (рис. 5, б):

0 < Ф 1 < Ф 2 < Ф 3 . (46)

Пусть H — расстояние от источника до первой сетки зеркала, а буквам Q ₁ , Q ₂ , Q ₃ придадим значения

Q i = qФ₁, Q ₂ = qФ 2 , Q 3 = qФ з . (47)

Запишем физическое время пролета t_D в той расстановке членов, как это следует из последовательного рассмотрения движений на разных участках. Получим

tD = н Im + 242ml^-(4E -EeQ^)+

EQ ₁

+ N^mT 1 2 ( V E-Q 1 —V e — Q 2 ) +

Q 1 Q 2

+ 242m   ie _ q .                    (48)

Q 3 - Q 2 ^N

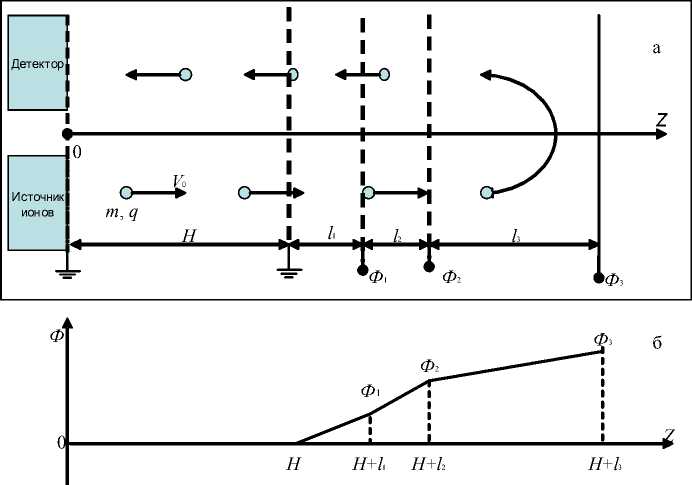
Рис. 5. Масс-рефлектрон с тройным зеркалом (а) и профиль потенциала в нем (б)

При Q1 ^ Q2 коэффициенты в (44) становятся сингулярными, и требуется переход к пределам, что, собственно, сильно отличает эту ситуацию от предельных выражений, соответствующих ситуации двух дрейфовых промежутков. Снова положим tD = H\mK (w),(49)

Q ₁

где

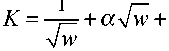
в 'J w - 1 + у A w - S

E      Q2

w = —, S = ^2, a = —1,

Q1       Q1

Окончательные выражения для решений таковы:

„ 5S - 2 w (S +1)      2Sw   .2 c =----------------, ri =-----, X =--. (56)

S               S - 1’ S ( S - 1) ^v '

Подставляя в (54) эти формулы, получим искомые a, в, Y, задающие условия фокусировки третьего порядка в системе. Но мы в них сейчас не d4K нуждаемся, а для вычисления сначала при-dw4

ведем все к параметрам С,П,X, чтобы пользоваться простыми выражениями (56). Итак, имеем d4K = 15 f Т_ d w4   16 w 92

a в П

77  7

w ²² ( w - 1 )²² ( w - S )²²

. (57)

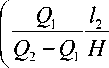
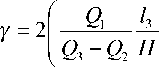
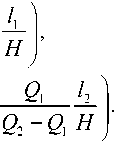
В параметрах С , П , X

d⁴ K 15 f„ , 4^ =9/1 ^{7 - C d w} 16 w ⁹² 1

w

Встраивание (56) в (58) дает

w w - S

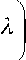
Структурно функция (50) очень сильно отличается от (34), поэтому и требуется отдельный подход. Вычисляем d4K dw4

_ 15 S + w ( S + 1)    w‘

S

dK 1 f 1 a в у ) ---= ---+     + ,      + ,       , d w  2 ^ w 2  ww  A w -1  A w - S J d2 K _ 1 f 3 a в y

--- — — --------------- 2     53       3       3, dw   4 [ w2   w92  (w -1)2 (w - S y2

d ³ K  3 ^f 5 a в y

=        7-7 +5y +ту +ту dw   8 [  w 92  w 92  (w -1) 92  (w - S У2

8 w ²

S

-

S - 1 [ S ( X - S ) w - 1

. (59)

Это выражение счастливо упрощается, и в итоге имеем

_d4 _K d w ⁴

15 S

8 w⁹² ( w - 1 )( w - S )

Приравнивая правые части (53) нулю, мы получим некую линейную систему с иррациональными коэффициентами, которую приведем к рациональной форме подстановками, похожими на (38):

a = ^C , в = ⁽ w _7/) Л , y = ( w J X ■ (54) w         _w 2 _w 2

По физическому смыслу S >  0 всегда и нигде в нуль не обращается, так что надежда на возможность фокусировки четвертого порядка за счет избыточного параметра S в данной модели рухнула. При любом выборе тормозящих потенциалов Ф ₁, Ф ₂, Ф ₃ достижима только фокусировка третьего порядка.

Вычислим теперь K в условиях фокусировки, используя (56), (54). Опять опуская элементарные выкладки, запишем:

Получающаяся система родственна (39):

K = ^S w ²

.

w A + ( w - 1)² ri + ( w - S )² X = w ²,

- w c + ( w - 1) n + ( w - S ) X = 3 w ,            (55)

^ + г/ + X = 5.

Определители здесь вычисляются достаточно просто, как и для (39), и мы не приводим выкладки.

Снова строим формулу разрешающей способности по массам m :

_2d4 _K

A m = 2 A K _ d w⁴ mK 4! K

Окончательно из (60, 61, 62) следует:

Am _ 5     (Aw)

m   64 w ² ( w - 1 )( w - S )

Мы получили удивительно простое обобщение Am формулы (44). Из нее следует, что m достигает минимума при наименьшем значении S и макси-Ф мально большом w. Но S = ф > 1 и минимум этой величины суть S = 1, что как раз отвечает формуле (40) и режиму дрейфа ионов в эквипотенциальном пространстве средней секции.

И еще раз убеждаемся, что только при w = 4 мы имеем фокусировку третьего порядка при вырождении 1-й секции в двойной слой из двух очень близко расположенных плоских сеточек, и разрешение при этом оптимально.

Мы здесь не даем исследования двух случаев:

• 1)    когда 1-я секция ускоряющая, а 2-я тормозящая;

• 2)    когда 1-я секция тормозящая, а 2-я ускоряю-

• щая, —

в силу того что они приводят к физически нереализуемым ситуациям.

Итак, мы сконструировали новую электроннооптическую схему времяпролетного масс-спектрометра под названием "модифицированный масс-рефлектрон" и показали, что она наилучшая в классе систем с тройным зеркалом и является своеобразным исключительным случаем, вырождением этого класса.