Модифицированный метод прямого поиска в оптимизационных задачах специальной структуры

В практике научных исследований процессов функционирования систем военного назначения зачастую возникает необходимость решения задачи оптимизации значений характеристик этих систем, функционирующих в различных условиях обстановки, по критерию минимальной стоимости при ограничении на требуемый уровень эффективности за располагаемое время. В общем виде математическая постановка подобных задач может быть представлена в виде

С( Χ опт ,Χ ср ) → min , ^Χ опт ^{∈ Ω}Χ

Э(Χопт,Χср)≥Этр,Т(Χопт,Χср)≤Трасп,Χопт ∈ ΩΧΧср ∈ ΩΧср, где С (X опт, X ср), Э (X опт, X ср), Т (X опт, X ср) - функции стоимости, эффективности и времени соответственно; Этр, Трапр - требуемые значения эффективности и располагаемого времени функционирования систем военного назначения; Хопт = (хопт1 ,...,хопте,..., хопт@) - вектор значений оптимизируемых переменных; Хср – вектор значений характеристик внешней среды; QX, Охср - область допустимых значений оптимизируемых переменных и значений характеристик внешней среды.

Анализ подобных задач показывает, что их особенность, как правило, состоит в том, что функции стоимости С(Хопт,Хср) и эффективности Э(Хопт,Хср) нелинейные. При этом чаще всего функция ограничений Э(Хопт,Хср) не может быть получена в явном виде, поскольку ее значения определяются на основе моделирования процессов функционирования исследуемых систем военного назначения, являющихся по своей сути сложными военно-техническими системами, при различных характеристиках внешней среды.

Механизм формирования вариантов внешней среды, принимаемых для моделирования, определяется спецификой функционирования рассматриваемых сложных военно-технических систем.

Внешняя среда характеризуется набором параметров различной природы. В военных системах военного назначения параметры могут быть сведены к основополагающим группам характеристик: характеристики противника, района военных действий и своих войск.

Г руппу характеристик противника составляют технические характеристики средств нападения и пространственно-временные характеристики операций противника. К характеристикам этой группы могут быть отнесены такие физические характеристики, как тактикотехнические характеристики средств нападения, характеристики обеспечивающих сил и средств и т. д.

Г руппа характеристик района военных действий включает метеорологические характеристики, характеристики коммуникаций, характеристики объектов, имеющих повышенную опасность, и т.д.

Группу характеристик своих войск составляют тактико-технические характеристики образцов оружия, характеристики боевых порядков, вариантов применения своих во-йск и т. д.

Учитывая вышеизложенные положения, вектор характеристик среды Хср можно представить как ср пр. р. .в).

где Х ср = ^{( Х} пр , ^Х р , Х св ) — векторы характеристик противника, района военных действий и своих войск соответственно.

В этом случае вектор значений характеристик противника будет иметь вид

где х^’-рх прп ,-, ^XnpN ^{- значения} характеристик противника; N ^- общее количество характеристик противника.

Аналогично можно записать вектор значений характеристик района военных действий:

х прnmin

≤ х_прn ≤ х_прnmax, ∀ n ∈ 1,N,

где х прnmin , х прnmax , х рkmin , х рkmax , х свlmin , х свlmax – минимальное и максимальное значения n -ой, n = 1, N характеристики противника, k -той, k = 1, K характеристики района военных действий и l -той, l = 1, L характеристики своих войск.

В дальнейшем допустим, что характеристики противника, района военных действий и своих войск могут принимать счетное количество значений в интервалах (6) так, что n -я характеристика противника принимает A n значений V n е 1,N , к -я характеристика района военных действий - В _к значений V к е 1,K , l -я характеристика своих войск - C l значений V l е 1,L .

В результате для всех характеристик противника имеем суммарное число значений

N

АПР- '- для всех характеристик района военных действий имеем суммарное число значений

В z = S Вк(8)

рΣ k=1 k и для всех характеристик своих войск имеем суммарное число значений

L

Ссв ; = £ С1 .

l = 1

Кроме того, для упрощения рассуждений в дальнейшем будем полагать, что возможны любые сочетания рассматриваемых характеристик (на практике это не всегда выполняется).

На рис. 1 показан механизм формирования вариантов среды с различными значениями параметров противника.

Мы видим, что число возможных вариантов среды равно числу сочетаний из общего числа возможных значений всех переменных A_прЕ (выражение 6) по числу временных параметров N , т.е.:

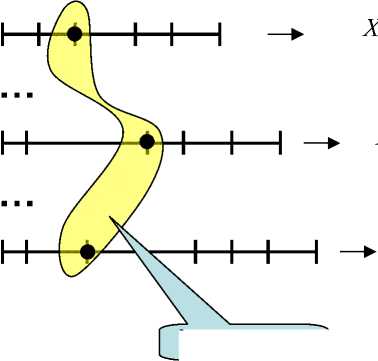
Хпрn ⇒ Аn пр1 ⇒ А1

Вариант характеристи противника

Рис. 1. Механизм формирования вариантов среды с различными значениями характеристик противника

Х _прN ⇒ А _N

Nпр 1= С A .(10)

пр Σ

Аналогично формируются варианты среды района военных действий:

Nр . = СВ.

и параметров своих войск:

Nсв .= ССсв. .(12)

Каждый i-й, i е 1, Nпрz , вариант среды с различными значениями характеристик противника является элементом множества возможных вариантов – Ω . Аналогично каждый j-й, пр j е 1, NрЕ , вариант среды с различными значениями параметров района военных действии есть элемент множества возможных вариантов — Пр и каждый q-й, q G1, Ncez , вариант среды с различными значениями пространственных параметров своих войск — элемент множества возможных вариантов Псв-

Полагая, что значения характеристик противника, района военных действий и своих войск принимают значения независимо друг от друга, можно рассчитать число возможных вариантов внешней среды N Σ :

N = С 3                                                        (13)

2      ( N _+ N _+ N „)

^v пр 2 р 2 св 2⁷

На рис. 2 схематично показан механизм формирования варианта внешней среды.

Мы видим, что формирование вариантов внешней среды осуществляется на основе выбора и объединения единичных элементов множеств Ω_пр, Ω_р, Ω_св. В качестве примера на рис. 2 (замкнутый контур) показан вариант внешней среды B _ij_q , имеющий i -й вариант характеристик противника, j -тый вариант характеристик района военных действий и q -й вариант характеристик своих войск.

Каждый B _ij_q -вариант внешней среды представляет собой вполне конкретную ситуацию для моделирования. Однако даже при самом приблизительном рассмотрении приходим к выводу о существовании большого множества таких ситуаций.

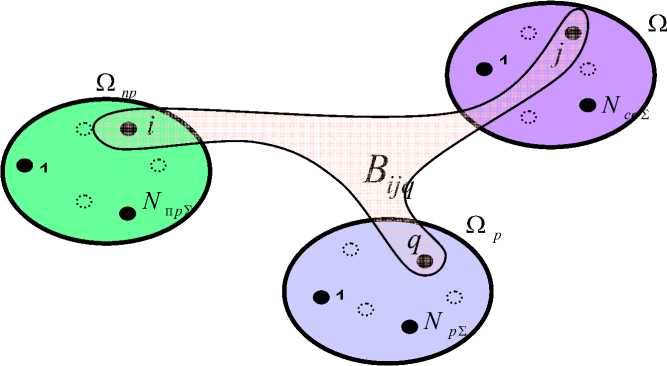
Рис. 2. Механизм формирования вариантов внешней среды

Так, например, допустим, что внешняя среда содержит по три ( N=K=L= 3) характеристики, каждая из которых может принимать по три значения А ф _Е - А _врЕ - А _прЕ = 9, в этом случае число возможных физических (временных, пространственных) вариантов среды согласно (10-12) составит

N. = N = N  = С N = С N = С N = С ³ = 84

^{ф £}       в р £       п р £       ^Аф ^{£       А}в_р ^{£       А}пр ^£       9         ^.

Тогда число вариантов внешней среды (ситуаций) согласно (13) будет равно

N Е = С N _Е+ N ep _е + N np, ) = С (384 + 84 + 84) = ^{2 6 3 5 5 0 0.} (¹⁵)

Естественно предположить, что в условиях такого числа ситуаций принять адекватное единственно правильное решение крайне затруднительно. При большем числе характеристик противника, района военных действий и характеристик своих войск, а также при возрастании количества значений каждой из них общее число ситуаций резко возрастает, приводя к невозможности получения хотя бы какого-то рационального решения.

Аналогичные рассуждения можно провести для составляющих вектора оптимизируемых переменных. В этих условиях зачастую прибегают к формированию счетного числа вариантов, в наибольшей степени отражающих характеристики внешней среды для рассматриваемой задачи, что равносильно декомпозиции оптимизационной задачи (1) на ряд самостоятельных задач.

Для каждого варианта значений характеристик внешней среды в результате решения оптимизационной задачи (1) может быть получено единственное множество оптимальных значений оптимизируемых переменных, в рамках принятых ограничений, в точке ( ° ) 0 - мерно го гиперкуба, ограниченного областью Q X , вида

О

опт

ОО  О

= ( x опт1 ,...,x оптθ ,..., x опт Θ ) .

При этом границы гиперкуба определяются в Θ – мерном пространстве минимальными и максимальными значениями вектора X опт:

x оптθ min ^≤ x оптθ ^≤ x оптθ max ^{, ∀ θ ∈ 1, Θ}

Отмеченные обстоятельства свидетельствуют о значительной размерности задач подобного типа, а невозможность получения целевой функции С( Х _опт, Х _ср) и функции ограничений Э^{( Х} о _пт, ^Х ср ) ^{в явном виде} свидетельствуют о том, что единственным методом получения ре^шения для подобных задач выступает метод прямого поиска, предполагающий на каждом шаге моделирования вычисление значения целевой функции и проверке результатов на удовлетворение ограничениям.

Среди методов прямого поиска зачастую применяются методы симплексов (Нелдера-Мида, модифицированные методы Нелдера-Мида), методы поиска Хука-Дживса, методы сопряженных направлений Пауэлла и др. [1-4]. Уже при размерности задачи Θ ≥ 10 требуются значительные затраты машинного времени.

В этих условиях методы симплексов значительно уступают методу Хука-Дживса по объемам требующихся вычислительных мощностей.

Сущность метода Хука–Дживса заключается в том, что из допустимой точки Χ∗опт ∈ ΩΧ по каждой характеристике исследуемой системы осуществляется последовательность шагов в сто-– 1234 – рону уменьшения и увеличения значений, составляющих вектора Xопт = (xопт1 ,...,x  xопт0), на величину Δxотп1. При этом значение характеристики снижающей значение целевой функции С(Хопт,Хср) и удовлетворяющей функции ограничений Э(Хопт,Хср) фиксируется и с этой точки, по следующей характеристике осуществляется уменьшение и увеличение ее значений на величину Axотп2. Значение 2-й характеристики снижающей значение целевой функции С(Хопт,Хср) и удовлетворяющей функции ограничений Э(Хопт,Хср) снова фиксируется и процедура повторяется Θ раз. В результате через Θ шагов получаем точку, из которой продолжается движение к минимуму целевой функции. Окончанием процедуры поиска минимума целевой функции является отклонение функции ограничений от требуемого значения на малую наперед заданную величину е такую, что

| ^Э„ - ^Э ( X „ , X ср ) |< £ .                                               (18)

Из физической сущности задачи (1) можно заметить, что возрастание значений каждой из оптимизируемых переменных приводит к возрастанию значений функций С( Х _опт, Х _ср) и Э( Х _опт, Х _ср), что указывает на их монотонный характер. Это обстоятельство позволяет снизить объемы вычислений по сравнению с классическим методом Хука–Дживса.

Поскольку функции Э( Х _опт, Х _ср) и С( Х _опт, Х _ср) являются монотонными функциями оптимизируемых переменных, Парето-оптимальная область решений имеет вид, представленный на рис. 3.

Парето-оптимальная область, изображенная на рис. 3, получается за счет многократного решения задачи (1) для различных значений Э_тр. Сущность модифицированного метода прямого поиска решения оптимизационной задачи (1) заключается в том, что каждая 9-я оптимизируемая переменная разбивается на N_θ равных частей ∆ x _оптθ , ∀ θ = 1, Θ , как показано на рис. 4.

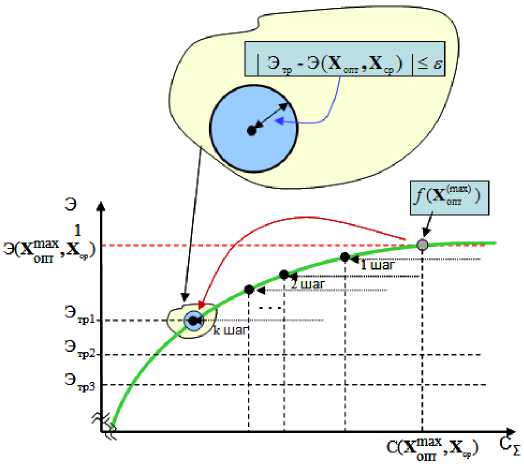
Рис. 3. Парето-оптимальная область решений

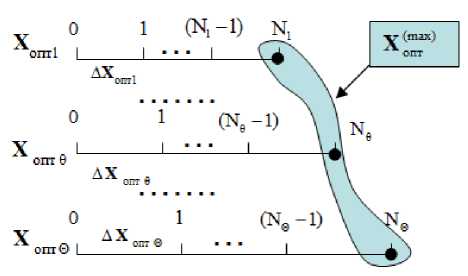
Рис. 4. Разбиение значений оптимизируемых переменных на равные части

Для целочисленных оптимизируемых переменных их значения составляют числа 0, 1, 2, …, N θ –1, N θ . Для непрерывных оптимизируемых переменных производится разбиение вида

0, & х опт ,2 А х опт ,...,^N . А х опт ,                                                  (19)

где Δ x опт – длительность единичного интервала разбиения.

Движение к минимуму стоимости осуществляется пошагово из точки X 0m ^ax) в пространстве оптимизируемых параметров (рис. 3, 4), соответствующей максимальным значениям каждой из оптимизируемых переменных Δ x _о^(m_пт^a_θ^x) (для каждого интервала с номером N θ , ∀ θ = 1, Θ ):

(max)          (N 1 )          (N θ )           (N Θ )

опт            опт1 ^,...,    опт θ ^,...,     опт Θ ^.

Изменение значений оптимизируемых переменных в сторону уменьшения приводит к снижению значений стоимости системы военного назначения (в силу монотонности функции стоимости С( Х _0ПТ , Х _ср ) (рис. 3), поэтому Парето-оптимальная область имеет монотонный убывающий характер. При этом соответственно снижается и значение показателя эффективности системы.

Далее последовательно осуществляется снижение значений каждого из оптимизируемых переменных на одну дискрету ( А х 0N _T “ ₉ ¹⁾ ) и производится моделирование функционирования исследуемой системы военного назначения в течение времени Т_расп с полученными значени ям и оптимизируемых переменных. При этом значение стоимости системы С( А х ONV) ), V 6 = 1, 0 (N -1)

и значение ее эффективности Э( Δ х _о ^(N _пт ^θ _θ ⁾ ) запоминается. На каждом шаге снижения значений каждого из оптимизируемых переменных значение эффективности проверяется на удовлетво-рениеусловию          _{(N -1)}

Э А X опт-,' >) а э т, .                                                               (21)

Если условие (21) выполняется, то из полученного ряда значений стоимости системы выбирается ее минимальное значение, а значение переменной, соответствующей минимальному значению стоимости, фиксируется, и процедура снижения значений остальных переменных повторяется. На каждом последующем шаге из полученного ряда значений стоимости системы выбирается ее минимальное значение и производится проверка на удовлетворение условию

Процедуры проводятся до момента, когда начинает выполняться условие (18):

| Э р - Э ( Х опт , Х ср ) <  8.

Модификация метода заключается в том, что в отличие от классического алгоритма метода Хука-Дживса движение в направлении минимума стоимости осуществляется путем изменения значений характеристик систем только в сторону уменьшения.

Известное направление поиска в сторону уменьшения значений характеристик системы и проверка удовлетворения ограничению по эффективности функционирования системы на каждом шаге позволяют значительно сократить область поиска значений опт1,...,х оптθ ,..., х оптΘ

Таким образом,представленный метод решения оптимизационной задачи (1) дает возможность определить множество значений характеристик исследуемой системы, обеспечивающих требуемую эффективность этих систем в заданных условиях при минимуме суммар -ных затрат на создание и функционирование в пределах располагаемого времени.