Модификация алгоритма структурно-параметрической оптимизации корректирующих устройств на основе амплитудофазоискажающих звеньев

Автор: Панков-Козочкин Павел Александрович

Журнал: Вестник Донского государственного технического университета @vestnik-donstu

Статья в выпуске: 5 (48) т.10, 2010 года.

Бесплатный доступ

Рассмотрены результаты модификации алгоритма структурно-параметрического синтеза квазиоптимального закона управления, основанного на методике оценки качества коррекции по вектору косвенных частотных показателей качества корректируемой системы. Добавление в вектор величины наклона ЛАЧХ в окне коррекции значительно повышает эффективность алгоритма, что подтверждает зависимость между прямыми и косвенными показателями качества линеаризованных систем управления.

Амплитудофазоискажающие звенья, частотные корректирующие устройства, структурно-параметрическая оптимизация

Короткий адрес: https://sciup.org/14249409

IDR: 14249409

Текст научной статьи Модификация алгоритма структурно-параметрической оптимизации корректирующих устройств на основе амплитудофазоискажающих звеньев

Введение. Ввиду простоты частотных методов синтеза САУ, предлагается для коррекции линеаризованных объектов управления (ОУ) использовать амплитудофазоискажающие звенья (АФИ-звенья), их настройки находить специально обученными искусственными нейронными сетями (ИНС) [1], ИНС обучать с учителем, а его получать с помощью программного средства, реализующего алгоритм поиска настроек корректирующего устройства (КУ). Таким средством, построенным на эвристическом алгоритме поиска экстремума сложной функции методом роящихся частиц [2], является программа LinCorr 2.0 [3], при этом реализуется алгоритм поисковой структурно-параметрической оптимизации КУ.

Основой алгоритма является использование в качестве функции Q качества коррекции САУ минимального значения среди элементов вектора косвенных и параметрических характеристик результирующей САУ:

Q = min( ω cp , γ , ω π , L , λ 11 , λ 12 , ξ 11 , ξ 12 ,..., λ n 1 , λ n 2 , ξ n 1 , ξ n 2 ) , (1)

где ω _cp, γ , ω_π , L — косвенные частотные показатели качества, определяемые по разомкнутой САУ; λ ₁₁, λ ₁₂, ξ ₁₁, ξ ₁₂,..., λ _n ₁, λ _n ₂, ξ _n ₁, ξ _n ₂ — параметры глубин коррекции и колебательности каждого из n - звеньев КУ.

Постановка задачи. Поскольку алгоритм поисковой структурно-параметрической оптимизации КУ должен обеспечивать коррекцию САУ с широким диапазоном свойств, то для испытания возможностей данной реализации алгоритма был проведен поиск настроек КУ для 30 параметрически (и, соответственно, динамически) различных моделей замкнутых САУ, передаточные функции неизменяемой части которых можно записать как

Wðí.÷(p) =1 p(b2p2 +b1p+b0), где Wðí .÷ — передаточная функция неизменяемой части разомкнутой САУ; b0 , b1 , b2 — коэффициенты передаточной функции.

Параметры b ₂, b ₁, b ₀ сгенерированы случайным образом для получения наибольшего разнообразия качества корректируемых моделей и вместе с исходными прямыми и косвенными показателями представлены в табл. 1.

Таблица 1

Параметры исходных моделей

омер модели	Коэффициенты знаменателя модели			Прямые показатели		Косвенные показатели
омер модели	b 0	b 1	b 2	t ðåã , с	σ , %	ω_cp , рад	γ , град	ω π , рад	L , дБ
	1 ,6923	1 ,4868	0 ,3674	5,2 492	5 ,66	0,5 607	62, 1362	2,1 462	16, 7115
	1 ,1490	1 ,1899	0 ,9489	26, 6164	5 0,57	0,8 858	20, 9959	1,1 004	3,1 722
	2 ,0900	2 ,0678	0 ,8893	3,7 699	4 ,96	0,4 698	62, 8408	1,5 33	13, 7323

1 ,8920	1 ,2707	0 ,1560	4,0 006	0 ,40	0,5 098	70, 7143	3,4 831	23, 7595
1 ,5173	1 ,5535	0 ,6101	5,8 727	1 6,04	0,6 23	52, 9183	1,5 771	11, 7401
0 ,9957	1 ,2446	0 ,4405	10, 9422	3 6,35	0,8 116	34, 9304	1,5 034	8,9 83
0 ,5253	1 ,0554	0 ,1461	13, 9782	5 3,92	0,9 378	21, 8459	1,8 96	11, 5816

Окончание табл.

омер модели	Коэффициенты знаменателя модели			Прямые показатели		Косвенные показатели
омер модели	b 0	b 1	b 2		b 0	b 1	b 2		b 0
	1 ,7741	1 ,7205	0 ,6294	5 ,8461	8 ,40	0,5 427	59, 5596	1,6 789	13, 7141
	1 ,0573	1 ,1088	0 ,1155	5 ,4238	1 8,53	0,7 666	49, 3338	3,0 254	20, 1284
0	1 ,1805	1 ,2275	0 ,9379	2 0,6939	4 7,20	0,8 601	24, 7429	1,1 219	3,7 79
1	0 ,9869	1 ,0555	0 ,9270	8 6,6142	6 5,53	0,9 704	6,3 533	1,0 318	1,0 131
2	1 ,4929	1 ,2978	0 ,2372	5 ,4148	7 ,65	0,6 189	60, 1935	2,5 089	18, 2437
3	2 ,1174	1 ,3064	0 ,1562	4 ,7923	0	0,4 609	73, 8846	3,6 814	24, 9619
4	2 ,0191	1 ,8484	0 ,5964	3 ,7534	3 ,08	0,4 806	64, 7207	1,8 4	15, 9289
5	1 ,5717	1 ,6174	0 ,7752	5 ,9081	1 7,97	0,6 171	51, 9752	1,4 239	10, 3158
6	1 ,0677	1 ,0808	0 ,0820	5 ,4126	1 6,75	0,7 626	51, 062	3,6 086	22, 9687
7	0 ,9680	1 ,2186	0 ,6093	1 4,4199	4 7,06	0,8 57	26, 4918	1,2 605	5,7 38
8	0 ,9316	1 ,0506	0 ,0579	5 ,3138	2 1,67	0,8 103	46, 3887	4,0 105	24, 5565
9	1 ,2926	1 ,1998	0 ,1794	5 ,4945	1 1,97	0,6 844	55, 8081	2,6 84	18, 7329
0	2 ,0990	1 ,2402	0 ,1215	4 ,8324	0	0,4 648	74, 4585	4,1 571	26, 6213
1	1 ,2879	1 ,2141	0 ,1961	5 ,5259	1 2,63	0,6 862	55, 1274	2,5 627	18, 0331
2	1 ,4755	1 ,0096	0 ,0066	3 ,0631	3 ,34	0,6 242	66, 8356	14, 9927	47, 1186
3	0 ,5195	1 ,0526	0 ,1378	1 4,0410	5 3,75	0,9 387	21, 9435	1,9 419	11, 974
4	1 ,5906	1 ,2205	0 ,1534	3 ,1730	3 ,83	0,5 892	64, 9309	3,2 196	22, 0431
5	0 ,4406	1 ,0326	0 ,0942	1 6,8469	5 7,18	0,9 546	19, 794	2,1 63	13, 6814
6	1 ,9032	1 ,9055	0 ,9518	6 ,0506	1 0,05	0,5 205	58, 9159	1,4 141	11, 619
7	2 ,0590	1 ,1245	0 ,0624	4 ,8169	0	0,4 732	75, 414	5,7 459	31, 3937
8	0 ,5340	1 ,0656	0 ,3426	2 9,6287	6 9,75	0,9 578	12, 1464	1,2 485	4,4 066
9	1 ,8006	1 ,7301	0 ,6167	5 ,7936	7 ,54	0,5 349	60, 3241	1,7 088	14, 0691
0	1 ,2125	1 ,3619	0 ,5310	8 ,3875	2 7,27	0,7 338	42, 835	1,5 111	9,8 539
	1 ,7741	1 ,7205	0 ,6294	5 ,8461	8 ,40	0,5 427	59, 5596	1,6 789	13, 7141

Результаты поиска структуры и настроек частотным КУ для данных моделей приведены в табл. 2. Для ряда моделей были определены сразу два решения — минимальное и неминимальное по структуре, и эти пары решений дали приблизительно равный результат. Однако результаты коррекции для разных моделей сильно отличались и, кроме того, во всех случаях достичь требуемого времени регулирования (~1 с) не удалось — наиболее близкий к эталонному результат получен только для модели 25: t рег = 1,5286 с.

Таблица 2

Результаты коррекции исследуемых моделей

Н омер модели	П орядок КУ	Косвенные показатели				Прямые показатели
Н омер модели	П орядок КУ	ω _cp , рад	γ , град	ω_π , рад	L , дБ	t рег , с	σ , %
1	2	3,0449	105,2041	78,0306	37,9089	8,8872	0
2	2	2,7455	88,7201	76,3054	35,4140	6,436	0
2	3	2,9821	102,8800	103,9789	37,0468	6,672	0
3	2	2,8806	98,7871	61,0656	35,6164	11,0163	0
4	2	3,2354	111,7804	95,4405	40,2787	9,9821	0
5	2	2,8947	100,0119	70,9047	36,0382	7,9322	0
6	2	2,8987	100,1510	80,4915	36,0883	5,1347	0
6	3	3,2259	108,8572	120,6251	39,2980	4,9275	0
7	2	3,0087	103,9526	106,5122	37,4581	1,9173	0
8	2	2,9211	100,9211	68,3609	36,3658	9,2931	0
9	2	3,1415	108,5519	108,9429	39,1034	5,72	0
1 0	2	2,7010	89,5375	76,1150	35,6275	6,5061	0
1 0	3	5,6686	95,5453	120,6139	37,9604	7,5374	0
1 1	2	3,2103	86,7812	73,5264	33,2813	6,0945	0
1 1	3	3,2921	100,3331	113,0557	36,1607	5,8574	0
1 2	2	3,1109	107,4749	88,0310	38,7267	7,9298	0
1 3	2	3,2621	112,7059	94,1081	40,6123	11,0631	0
1 4	2	2,9636	102,3911	67,4580	36,8957	10,5946	0
1 5	2	2,8353	97,8761	67,1762	35,2673	8,1963	0
1 5	3	3,2075	110,4969	119,9604	39,5387	8,092	0
1 6	2	3,1729	109,6230	120,8398	39,5018	5,8392	0
1 7	2	2,7708	95,6644	78,2459	35,6045	5,0858	0
1 7	3	3,1433	108,5971	142,2258	39,1398	5,109	0

Окончание табл. 2

Н омер модели	П орядок КУ	Косвенные показатели				Прямые показатели
Н омер модели	П орядок КУ	ω cp , рад	γ , град	ω_π , рад	L , дБ	t рег , с	σ , %
1 8	2	3,1731	109,2776	136,1956	39,3777	5,0429	0
1 9	2	3,1284	108,0876	95,7558	38,9481	6,9438	0
2 0	2	3,2976	113,9480	101,1239	41,0480	11,01	0
2 1	2	3,1138	107,5805	93,6963	38,7654	6,8993	0
2 2	1	2,3447	81,0303	27,1249	36,0639	7,6888	0
2 3	2	3,0137	104,1208	108,4382	37,5188	1,8729	0
2 4	2	3,1967	110,4525	97,6514	39,7984	8,5075	0
2 5	2	3,0299	104,4174	120,7188	37,6276	1,5286	0
2 6	2	2,8196	97,4166	61,8190	35,0991	9,9466	0
2	3	3,0372	93,7818	38,6247	34,0829	9,5486

6							1,04
2 7	2	3,3662	116,2952	125,9321	41,9558	10,9232	0
2 8	2	2,8722	99,2366	88,9609	35,7587	2,1076	0
2 9	2	2,9298	101,2242	68,4730	36,4750	9,4347	0
3 0	2	2,8857	99,7028	75,6567	35,9267	6,325	0

Анализ результатов (см. табл. 2) показывает, что для сильно колебательных ОУ (например, 2, 11, 25) в результате коррекции значительно улучшается вид переходного процесса (ПП), что выражается в уменьшении перерегулирования и времени регулирования. Однако для изначально «хороших» ОУ с гладким видом ПП происходит обратное — увеличение времени регулирования. При этом характерный вид ПП результата коррекции для большинства из рассмотренных моделей САУ третьего порядка выглядит так, как это показано на рис. 1, а .

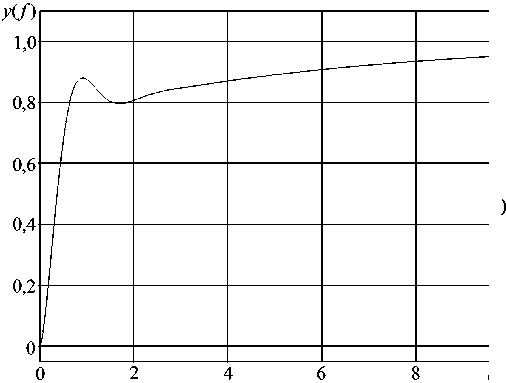
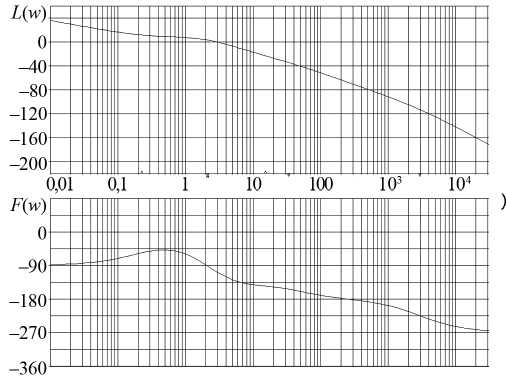
Рис. 1. Типичные характеристики результата коррекции: а — переходная; б — амплитудно- и фазочастотная

Решение задачи. Подробный анализ частотных характеристик результатов (рис. 1, б ) показал, что в данной реализации алгоритма состав вектора [см. формулу (1)] функции качества Q допускает появление резонансных подъемов ЛАЧХ на некоторых участках, отвечающих за «горбатый» вид ПП и последующее его «затягивание» (рис. 1, а ). Кроме того, в структуре КУ не предусмотрен важный параметр — его собственный коэффициент усиления, отличный от единицы. Это также уменьшает возможность получения требуемого результата коррекции.

Для устранения указанных недостатков принято решение добавить в состав функционала качества Q следующие косвенные оценки качества:

— наклон ЛАЧХ в точке пересечения с осью частот L '( ® _cp) ;
— наклон ЛАЧХ в зоне коррекции L ‘ ₁₈ в целях контроля резонансных свойств КУ.

Кроме того, в совокупность варьируемых параметров КУ необходимо ввести собственный коэффициент усиления и варьировать при поиске наравне с остальными настройками.

Для реализации введенных модификаций был усовершенствован алгоритм поиска, выполненный в виде программного средства LinCorr 2.2, а для его проверки взяты те же 30 моделей (см. табл. 1), что и для версии 2.0. Результаты поиска представлены в табл. 3, где в составе косвенных показателей есть указанные выше параметры наклона ЛАЧХ.

Таблица 3

Результаты поиска с помощью обновленной программы

омер модел и	орядо к КУ	Косвенные показатели						Прямые показатели
омер модел и	орядо к КУ	т ₍ , рад	γ , град	ω _π , рад	L , дБ	L ' ( ® с , дБ/дек	Lк , дБ/дек	t 8а , с	, %
		2,4568	82,5154	33,4826	31,8902	–18,448	–18,379	1,2295	0,07
		2,0963	84,3680	32,8980	26,7945	–20,109	–18,702	1,2514	0,77
		2,4510	84,1300	41,0789	30,3226	–20,025	–18,973	1,1833	0,11
		2,4925	84,0773	41,1067	30,5776	–19,753	–18,834	1,1524	0,32
		2,3646	81,6894	30,1591	29,4612	–18,640	–18,574	1,1161	0,96
		2,3580	82,1513	30,0080	29,1543	–19,579	–18,744	1,244	0,06
		1,9448	68,5183	13,1339	24,4442	–21,911	–21,944	0,9981	1,55
		2,2197	77,9337	24,1285	28,3645	–20,082	–19,328	1,1699	0,00
		2,4324	83,9354	34,6615	30,5535	–18,950	–18,337	1,2892	0,11
		2,4943	85,1157	39,4867	30,8377	–19,276	–18,566	1,3017	0,00
		2,7005	90,5445	111,5154	41,3716	–18,970	–18,675	1,3098	0,00
		2,8847	81,6119	41,5925	29,3595	–20,534	–18,778	0,9685	0,00
		2,6685	89,8188	118,9090	42,3224	–18,742	–18,605	1,2062	0,00
		2,4106	83,1569	32,3571	29,9850	–19,016	–18,559	1,2502	0,08
		2,3921	82,0508	32,6970	31,3969	–19,292	–19,163	1,2482	0,00
		2,6615	82,8237	55,1082	40,1245	–18,457	–18,340	1,2415	0,00
0		2,4546	83,6187	40,4960	31,1579	–20,131	–18,304	1,2144	0,14
0		2,5872	84,1230	40,5573	30,5223	–19,717	–18,851	1,1842	0,00
1		2,5262	84,5838	43,0394	30,6964	–19,401	–18,353	1,1196	0,93
1		2,4549	83,7430	42,9450	30,1462	–20,442	–18,610	1,1483	0,05
1		2,4768	84,3447	43,0172	30,5944	–19,356	–21,599	1,105	1,14
2		2,4993	84,0712	35,6920	30,7944	–18,557	–18,296	1,1517	0,29
2		2,1851	77,2036	20,4653	26,8604	–20,078	–19,371	1,1391	0,01
3		2,0125	69,1389	13,6166	24,5024	–21,632	–21,820	0,9749	0,99
3		2,1670	74,3589	18,2329	24,1404	–20,278	–19,781	1,0508	0,00
4		2,4057	82,4490	30,6560	29,9099	–18,537	–18,472	1,1946	0,32
5		2,1311	70,3701	35,9334	40,7703	–19,020	–18,383	0,8766	3,10
5		1,9678	67,6171	17,9403	30,5154	–21,000	–18,923	0,9972	1,87
6		1,9207	71,0029	14,6784	23,9590	–21,939	–21,937	1,0576	2,19
6		2,5528	86,6629	45,7961	32,2739	–19,042	–18,332	1,1866	0,00
7		2,4800	85,1879	40,5767	30,6458	–18,614	–18,313	1,1604	0,97
7		2,3725	83,0654	40,2366	29,6823	–21,493	–18,292	1,2706	0,00
8		1,9688	72,5135	16,2414	24,4372	–21,647	–21,791	1,0595	2,07

9	2,8333	84,2849	37,3675	30,3413	–18,777	–18,370	1,2046	0,00
0	2,0239	71,0290	15,3984	25,1963	–21,623	–21,864	1,0124	0,66
1	2,4307	81,0871	34,5297	34,1077	–18,358	–18,352	1,1906	0,17
2	2,4234	83,7282	46,9204	36,4093	–19,286	–18,391	1,3614	0,00
3	2,7364	86,0624	43,3271	30,6811	–19,220	–18,492	1,2069	0,00
4	1,8839	69,5475	12,1361	23,4536	–21,483	–21,466	1,0551	0,66
4	2,3020	80,8806	46,1624	39,9388	–18,577	–18,541	1,2199	0,26

Окончание табл. 3

омер модел и	орядо к КУ	Косвенные показатели						Прямые показатели
омер модел и	орядо к КУ	т ₍ , рад	γ , град	ω _π , рад	L , дБ	L ‘ ( ® с , дБ/дек	L si , дБ/дек	t 8а , с	, %
5		2,7946	85,9885	45,8388	30,8812	–19,376	–18,812	1,1326	0,00
6		2,3956	82,5004	31,6561	29,7590	–18,993	–18,463	1,1899	0,49
6		2,0525	70,1202	32,8361	40,5763	–20,087	–18,396	0,951	1,52
7		2,1663	74,7193	21,6101	26,7295	–21,659	–21,727	1,0251	0,73
8		2,5174	86,5536	43,0824	31,7923	–18,905	–18,619	1,3858	0,00
9		2,4279	82,6366	32,2852	30,5829	–18,547	–18,352	1,2045	0,35
9		2,4950	85,9154	88,5911	41,5149	–18,803	–18,345	1,1891	0,57
9		2,4116	83,0751	32,2039	30,0016	–18,713	–18,539	1,2148	0,25
0		2,4524	84,5727	37,6290	30,8044	–18,716	–18,528	1,2175	0,35
0		1,9897	81,5255	21,8268	26,8283	–21,020	–21,006	1,6808	0,00

Для всех моделей, имевших изначально разные свойства, получены достаточно близкие результаты коррекции по времени регулирования, перерегулированию и косвенным показателям качества (табл. 3). Кроме того, значения t _8аа всех результатов коррекции близки, а в некоторых случаях даже меньше времени регулирования эталонной САУ — t 8'_аа « 1 с. Форма ПП для всех результатов, в отличие от результатов теста предыдущей версии (см. рис. 1), является близкой к гладкой апериодической, с малым перерегулированием или же его отсутствием, что видно на графиках ПП для моделей с максимальным (рис. 2, а ), средним (рис. 2, б ) и минимальным (рис. 2, в ) временем регулирования. Некоторый разброс результатов коррекции по времени регулирования и перерегулированию обусловлен относительной мягкостью требований к эталонной системе.

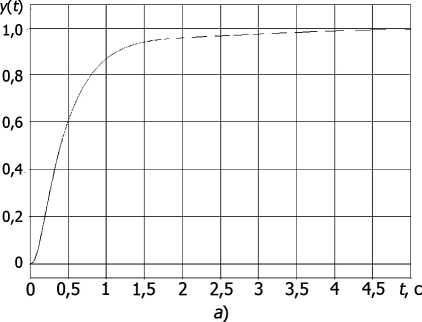
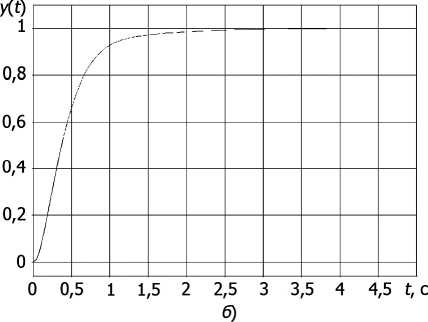
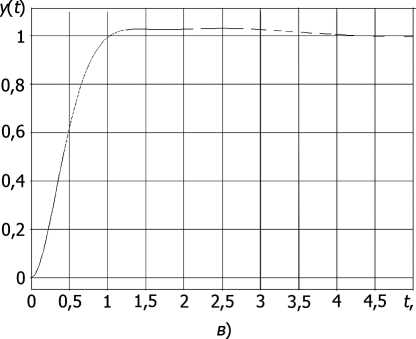
Рис. 2. Переходные процессы результатов коррекции: а — для модели 30; б — для модели 4; в — для модели 15

Выводы. Среди результатов есть как структурно-минимальные, так и структурнонеминимальные решения для одной модели (см. табл. 3). При этом увеличение порядка КУ не означает улучшения качества коррекции (например, модели 1, 3, 4 и т. д.), что говорит о необходимости поисковой оптимизации настроек метода роящихся частиц. Необходимо учитывать, что поиск настроек производится в пространстве переменной размерности (2 n + 1) , где n — порядок КУ, а следовательно, число особей роя с ростом размерности КУ также должно увеличиваться.

Полученные результаты подтверждают достаточно сильную и, возможно, близкую к однозначной связь между указанной выше совокупностью косвенных показателей качества разомкнутой САУ, включая наклоны ЛАЧХ, и ее характеристиками в замкнутом состоянии. При наличии такого вспомогательного средства, как программа LinCorr 2.2, есть вероятность установить в дальнейшем эту связь даже с помощью методов классического регрессионного анализа.

Список литературы Модификация алгоритма структурно-параметрической оптимизации корректирующих устройств на основе амплитудофазоискажающих звеньев

Нейдорф Р.А., Панков-Козочкин П.А. Быстрый алгоритм структурно-параметрической оптимизации корректирующих устройств на основе амплитудофазоискажающих звеньев//Вестник ДГТУ. -2009. -Т. 9. -Спец. вып. -С. 17-26.
Панков-Козочкин П.А. Алгоритм подготовки задачи нейросетевой оперативной коррекции САУ//Тр. конгресса по интеллектуальным системам и информационным технологиям «AIS-IT'09». -Т. 3. -М.: Физматлит, 2009. -С. 290-295.
Нейдорф Р.А., Панков-Козочкин П.А. Структурно-параметрическая оптимизация ресурсов управления//Изв. ЮФУ. Технические науки. Тем. выпуск «Методы и средства адаптивного управления в энергетике». -Таганрог: Изд-во ТТИ ЮФУ. -2010. -№ 1 (102). -С. 123-129.
Neidorf R.A., Pankov-Kozochkin P.A. Bystryi algoritm strukturno-parametricheskoi optimizacii korrektiruyuschih ustroistv na osnove amplitudofazoiskajayuschih zven'ev//Vestnik DGTU. -2009. -T. 9. -Spec. vyp. -S. 17-26. -in Russian.
Pankov-Kozochkin P.A. Algoritm podgotovki zadachi neirosetevoi operativnoi korrekcii SAU//Tr. kongressa po intellektual'nym sistemam i informacionnym tehnologiyam «AIS-IT'09». -T. 3. -M.: Fizmatlit, 2009. -S. 290-295. -in Russian.
Neidorf R.A., Pankov-Kozochkin P.A. Strukturno-parametricheskaya optimizaciya resursov upravleniya//Izv. YuFU. Tehnicheskie nauki. Tem. vypusk «Metody i sredstva adaptivnogo upravleniya v energetike». -Taganrog: Izd-vo TTI YuFU. -2010. -№ 1 (102). -S. 123-129. -in Russian.

Еще

Статья научная