Модификация частотно-временных описаний нестационарных процессов на основе показательных и степенных функций

В настоящее время большое внимание уделяется разработке принципов построения измерительных приборов и автоматов, предназначенных для анализа нестационарных процессов и оценивания их параметров. Подобные устройства находят широкое применение, например, при обработке сигналов, поступающих от специализированных датчиков (сейсмодатчиков, охранных систем и др.). Как правило, исследование нестационарных сигналов только во временнóй или в частотной области не обеспечивает достаточного количества информации для принятия правильного решения. Именно это привело к разработке такого мощного средства анализа, как спектрограммы, которые позволяют представлять исследуемые процессы в координатах частота—время на основе вычисления их матриц распределения энергии (РЭ) [1]. Вместе с тем известные недостатки спектрограммы, получившей название кратковременного преобразования Фурье (КПФ), не позволяют в полной мере обеспечить точное измерение характеристик быстро изменяющихся процессов [2]. Это обусловлено тем, что уменьшение размера времен-нóго окна, так чтобы оно позволяло локализовать такие изменения сигнала, приводит к неизбежному снижению локализации его энергии вдоль линии мгновенных частот в соответствии с принципом неопределенности Гейзенберга. Кроме того, в большинстве случаев исследуемые сигналы подвержены воздействию шумов различной интенсивности, что приводит к ошибкам измерений.

Возможные подходы к улучшению локализационных свойств совместных частотно-временных распределений (ЧВР) предложены в [3]. Также существенного улучшения характеристик частотно-временных описаний нестационарных сигналов можно достичь за счет использования методов, основанных на использовании непрерывных вейв-лет-преобразований [4].

Цель данной работы: на основе существующих подходов к формированию частотно-временных преобразований (ЧВП) определить пути их модификации для повышения качества измерений параметров нестационарных процессов в условиях воздействия шумов.

ПРЕДСТАВЛЕНИЕ ПРОЦЕССОВ НА ОСНОВЕ ИХ СОВМЕСТНЫХ ЧАСТОТНО-ВРЕМЕННЫХ ОПИСАНИЙ

В настоящее время уже известны различные приложения псевдо-ЧВР класса Коэна к решению технических задач [5, 6, 7]. Некоторые аспекты применения ЧВП представлены в № 2 и 3 за 2002 г. и 1 за 2004 г. журнала "Научное приборостроение". Практическое применение базовых ЧВР для решения задач измерения параметров нестационарных процессов подробно рассматривалось в № 3 за 2000 г. и № 1 за 2001 г. этого журнала.

В [5] для количественной оценки качества частотно-временных описаний выбраны такие показатели, как глобальный и локальный разбросы энергии. Однако их аналитическое вычисление является достаточно сложной задачей. Более того, даже для одного и того же частотно-временнóго преобразования расчетные выражения и конечные значения этих показателей различны и зависят от вида сигнала. Поэтому целесообразно рассмотреть указанные выше, а также другие варианты ЧВП с точки зрения степени их близости к "идеальному ЧВР", т. е. соответствия исходному процессу. В качестве "идеального ЧВР" предлагается распределение, вся энергия которого сосредоточена вдоль линии мгновенной частоты обрабатываемого процесса. Для тестового сигнала (рис. 1) вид матрицы РЭ "идеального ЧВР" приведен на рис. 2.

Базовым ЧВП класса Коэна является распределение Вигнера

”

W В ( f , t ) = M t - - • s | t + - • e ^- j2 ^{n f T} d T . (1) I 2          2

-”

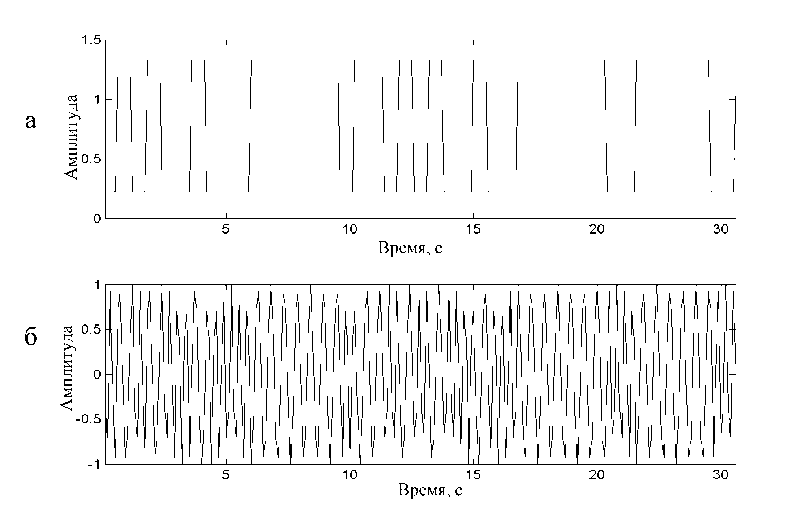
Рис. 1. Осциллограммы: первичный электрический сигнал (а) и тестовый сигнал-гармоника, модулированный первичным электрическим сигналом (б)

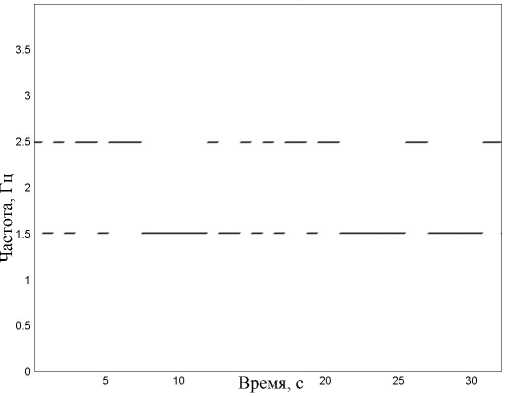
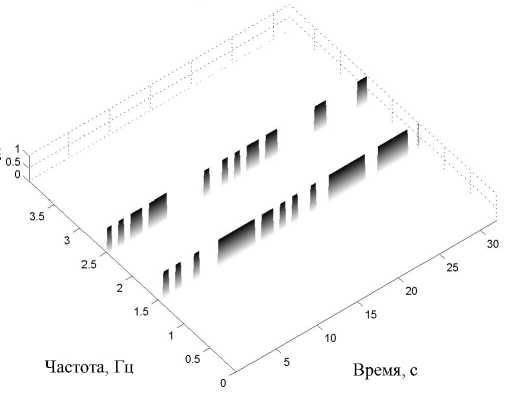
Рис. 2. Матрица РЭ тестового сигнала на основе "идеального ЧВР" в 2-мерном (а) и 3-мерном (б) представлениях

б

Данное распределение обладает свойством максимальной концентрации энергии сигнала в континууме точек его мгновенных частот. Однако в наибольшей степени указанным преимуществом удается воспользоваться при исследовании сигналов с линейным законом изменения частоты. При анализе процессов, имеющих несколько компонент в матрице РЭ, вычисляемой в соответствии с (1), появляется сильный интерференционный фон, затрудняющий их дальнейшую обработку [2] (см. Приложение, рис. П1).

С целью подавления паразитных составляющих, искажающих истинную картину матрицы РЭ анализируемого сигнала, в ядро ЧВР вводят оконные функции h ( t ) , например функцию Хэмминга:

h(t)= 0.54 - 0.46 • cosI 2n t )

n - 1 _j

при t = 0,..., n - 1, где n — размер окна.

Полученное таким образом выражение для вычисления псевдо-ЧВР Вигнера имеет следующий вид:

техX / X

~          f —     I

W В ⁽ f , t ) = ^s I t-- • h I ^-- ^x

I 2       I

-те X / X /

x sf t + — )• hf—)• e j2n fT d—

I 2 I I 2 I

В Приложении на рис. П2 представлены матрицы РЭ тестового сигнала, вычисленные на основе псевдо-ЧВР Вигнера. Вид матриц РЭ показывает, что при выборе даже достаточно широкого окна, с тем чтобы получить требуемое частотное разрешение, полностью подавить интерференционный фон в псевдо-ЧВР Вигнера не удается (рис. П2, а).

Другим широко известным ЧВП сигналов является КПФ те wс (f, t)= Js—)•h(t -1)• e"j2” f T dT , (3) -^

где s ( t ) — анализируемый сигнал, h ( t ) — временнóе окно (рис. П3). Анализ результатов, представленных на этом рисунке, показывает, что при выборе достаточно широкого окна, обеспечивающего требуемое частотное разрешение (рис. П3, а), быстрые изменения сигнала локализуются неточно. Причем положение максимума энергии в этом случае не соответствует истинному значению мгновенных частот, а представляет усреднение в пределах временнóго окна. Напротив, выбор узкого окна (рис. П3, б) обеспечивает приемлемое временнóе разрешение, но в этом случае спектральные составляющие недопустимо размыты во всей полосе анализа, поскольку частотного разрешения уже явно недостаточно.

Еще одним известным подходом к получению совместных частотно-временных описаний является непрерывное вейвлет-преобразование (НВП). Аналитическое представление НВП можно интерпретировать как скалярное произведение анализируемого сигнала s ( t ) и базисных функций ^ ( t )

те

W ВП ⁽ a , b ) = J ^{s ( t} ) У a , b ^{( t} ) ^d t .             ⁽⁴⁾

-те

Здесь y _ab ( t ) — материнский вейвлет, из которого с помощью сжатий (растяжений) и сдвигов формируют все семейство базисных функций декомпозиции:

V a ь ( t ) = a"^1!2V ^f t— b 1 , a , b ^ R , У e L ² ( R ) , (5)

, I. a J где a — масштаб вейвлета (аналог частоты в анализе Фурье); b — величина сдвига вейвлета вдоль оси времени; L2 (R) — гильбертово пространство [5].

В отличие от преобразования Фурье в НВП конкретный вид вейвлета не оговаривается, однако при соответствующем выборе базисной функции существует однозначное соответствие значения масштаба a и частоты анализа f. Одним из широко известных вейвлетов является функция Морле — гармоника, модулированная функцией Гаусса x       - x2

V a ⁽ x ) = exP^-

cos ( ax ) .

Таким образом, на основе НВП, так же как и на основе КПФ или ЧВР, можно рассчитать матрицы РЭ обрабатываемых сигналов. В соответствии со свойствами НВП полученные матрицы РЭ будут иметь приемлемое разрешение как на крупных, так и на мелких масштабах частоты (см. Приложение, рис. П4). В матрице РЭ, вычисленной на основе НВП Морле, величины временнóго и частотного разрешений зависят от частоты анализа. Положительным свойством такой матрицы является отсутствие в ней ложных пиков энергии и интерференционного фона.

МОДИФИЦИРОВАННЫЕ

ЧАСТОТНО-ВРЕМЕННЫЕ ОПИСАНИЯ

В результате поиска возможности улучшения локализационных свойств различных ЧВП было установлено следующее. При измерении параметров сигналов датчиков существенными являются доминирующие значения компонент в матрице РЭ, в то время как малые значения ее элементов преимущественно относятся к шумам, поскольку их энергия, как правило, равномерно распределена в частотно-временнóм пространстве. Следовательно, необходимо найти такое частотно-временнóе описание, которое позволило бы усилить доминирующие значения матрицы РЭ, другими словами, увеличить абсолютную разность между ними и величиной сопутствующих компонент. В радиотехнике аналогичные функции выполняет операция нелинейного усиления.

Среди известных математических операций, позволяющих осуществить требуемое нелинейное усиление, можно выделить преобразования на основе степенных и показательных функций. Очевидно, что применять такое преобразование желательно лишь к тем ЧВР, где нет ложных пиков энергии и значительного интерференционного фона. В противном случае паразитные выбросы также могут быть усилены, что крайне нежелательно.

В рамках рассмотренных ограничений указанным требованиям (из числа рассмотренных ЧВП) в полной мере отвечают КПФ и НВП (рис. П3, П4). Поэтому рассмотрим возможность применения к ним преобразования на основе показательной функции. Для этого сформируем модифицированную матрицу РЭ Kft = WСП (f, t), вычисленную с использованием КПФ при высоком временном разрешении (т. е. с малым размером n временного окна). Далее применим к ней показательную функцию следующим образом Kf t = A Kf • t, где A — некоторая выбираемая кон станта. Затем вновь полученную матрицу нормируем относительно ее полной энергии. Результирующие матрицы РЭ тестового сигнала, вычисленные на основе показательной функции от спектрограммы (ПФС), приведены на рис. 3.

Итоговое выражение для расчета любого модифицированного ЧВП можно представить в следующем виде:

W ^м ( f , t ) = [ A ^f ], (7)

где K f _t = W ( f , t ) — элементы матрицы РЭ, вычисленные, например, на основе КПФ; A >  1 — основание степени (в эксперименте A = 1000); при условии K f _t >  1 для любых f и t (для приведения

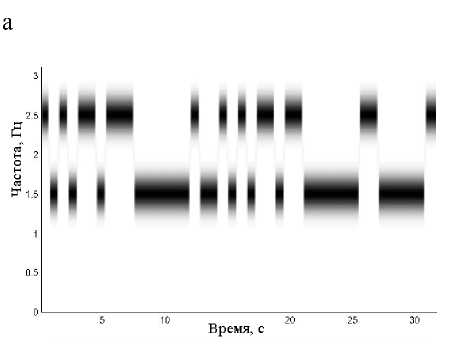
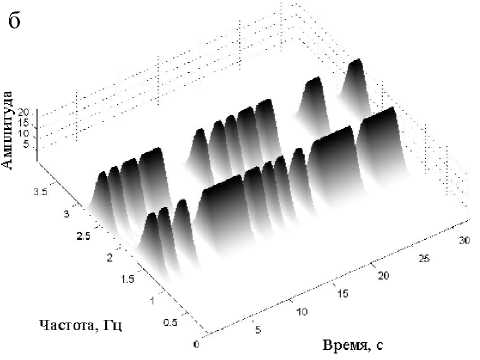
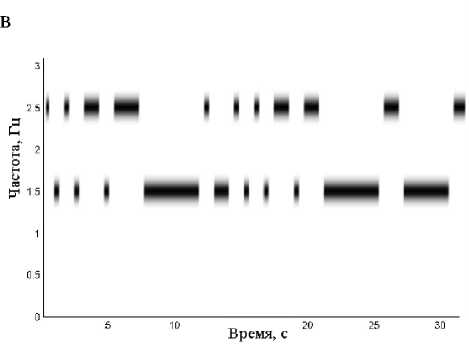
Рис. 3. Матрицы РЭ тестового сигнала, построенные на основе ПФС. а, б — 2- и 3-мерное изображения при n = 3;

в, г — 2- и 3-мерное изображения при n = 5

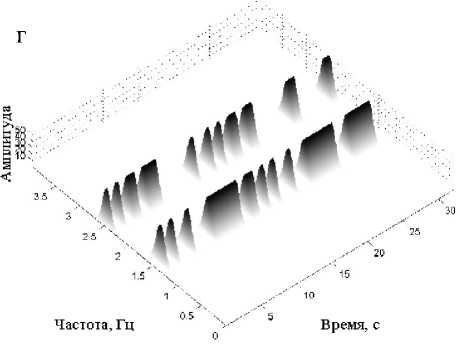
г

Частота, Гц

Время, с

матриц РЭ к данному условию может потребоваться проведение дополнительных операций над каждым элементом K _{f , t} : в частности, получение модуля и умножение на число, которые в целом не искажают общей картины РЭ). Частным случаем для ПФС будет использование A = e ~ 2.718, т. е. экспоненциальной функции от спектрограммы, вид которой близок к варианту A = 2.

Для оценки степени различия (схожести) реальных ЧВП с "идеальным ЧВР" выбран двумерный коэффициент корреляции r _к [6]

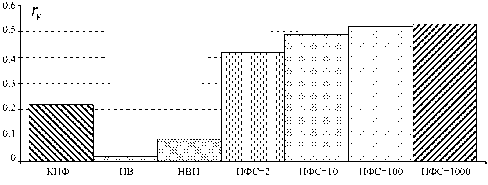
Рис. 4. Соответствие различных ЧВП "идеальному ЧВР" по метрике r _к

r _к

MN

TT ^Wm - n - w )^{( V}™ , n - v ) m = 1 n = 1

MN

H( w m , ,

-

M

N

W )2 TTK

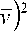
где w и v — математические ожидания элементов матриц.

Рассчитанные в ходе эксперимента значения метрики r _к для рассмотренных ЧВП приведены на рис. 4. Анализ результатов экспериментов, в том числе и представленных на рис. 4, показал, что максимальное соответствие "идеальному ЧВР" наблюдается у ПФС. Проведенные исследования показали, что основное достоинство НВП Морле и ПФС перед псевдо-ЧВР Вигнера состоит в отсутствии интерференционного фона в матрице РЭ. Поэтому они наиболее адекватно отражают час-тотно-временнýю структуру анализируемых процессов.

Результаты исследования ЧВП на основе ПФС позволили выявить в полученном частотно-временнóм описании значительное улучшение частотной локализации при сохранении высокого временнóго разрешения по сравнению со всеми наиболее известными ЧВР. Матрица РЭ от ПФС близка к "идеальному ЧВР" даже при минимальной ширине окна анализа (рис. 3). Это указывает на целесообразность их применения для измерения сигналов датчиков.

В качестве оконной использовалась функция Хэмминга шириной в 21 отсчет.

На основе сравнительного анализа матриц РЭ, было установлено следующее. При уменьшении отношения сигнал/шум (ОСШ) наблюдается значительное увеличение дисперсии в каждом частотном срезе матриц РЭ, приводящее к возникновению в них существенных отличий от матриц РЭ исходного (незашумленного) процесса. Однако при значениях ОСШ вплоть до 3 дБ доминирующие компоненты временных срезов матрицы РЭ зашумленного процесса по-прежнему точно соответствуют доминирующим компонентам соответствующих срезов матриц РЭ исходного процесса. Поскольку доминирующие компоненты временных срезов матриц РЭ исходного процесса, как правило, описывают полезный сигнал, то указанный факт можно использовать для их селекции в матрице РЭ зашумленного процесса.

В случае, если измерения касаются лишь временных и частотных параметров сигналов, то в целях такой селекции целесообразно осуществлять нормирование отдельно каждого временнóго среза матрицы РЭ W ( f, t ) относительно его максимального значения [8]

W ⁽ f , t ) = W ⁽ f , t ) /max W ⁽ f , t ) •

ОЦЕНКА РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ

ПОДХОДЫ К ПОВЫШЕНИЮ ПОМЕХОУСТОЙЧИВОСТИ ЧАСТОТНО-ВРЕМЕННЫХ ОПИСАНИЙ

Важным фактором практического применения ЧВР является их помехоустойчивость. Экспериментальное исследование помехоустойчивости осуществлялось для матриц РЭ, вычисленных на основе псевдо-ЧВР Вигнера, НВП Морле, КПФ и усовершенствованных ЧВП с использованием информации от двух спектрограмм [3] и ПФС.

Для сравнения помехоустойчивости матриц РЭ использован подход, принятый в практике оценивания потерь качества изображений после их сжатия [7, 8]. Целесообразность такого подхода определяется тем, что матрица РЭ по сути является изображением обрабатываемого процесса в координатах частота—время. В его основе лежит вычисление евклидовой нормы матрицы, найденной как разность матриц РЭ исходного и зашумленного сигналов

J = | W исх

-

зашумл

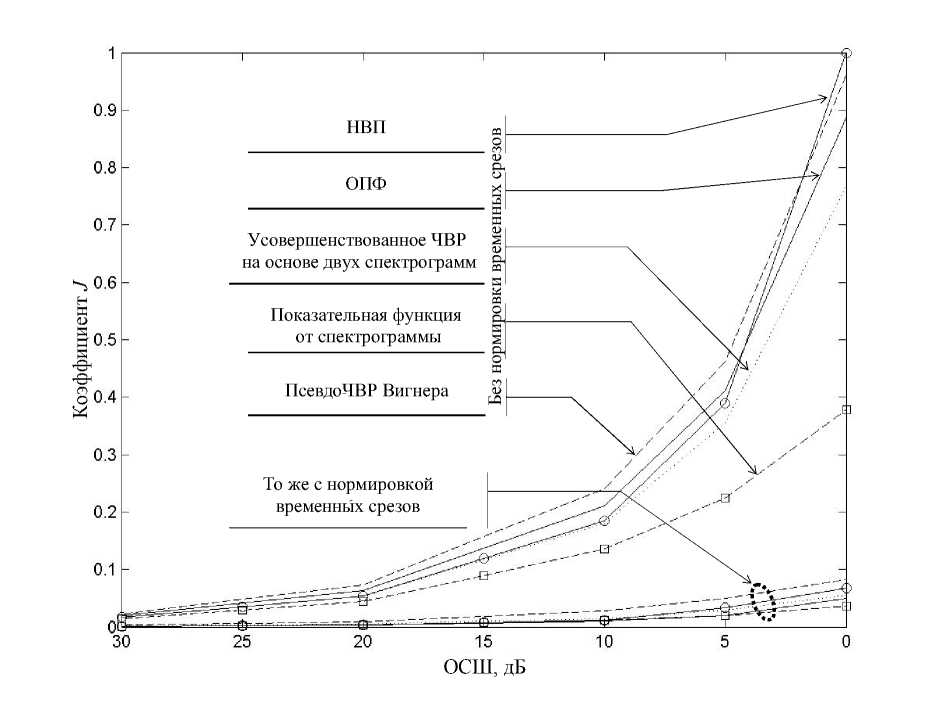
Рис. 5. Значения показателя РЭ радиосигналов к шумам устойчивости J матриц

где W _исх — матрица РЭ исходного (не зашумленного) процесса; W _зашумл — матрица РЭ зашумленного процесса.

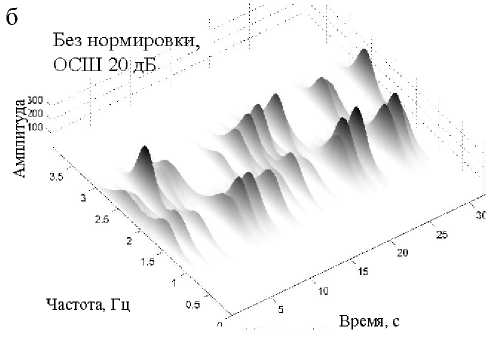
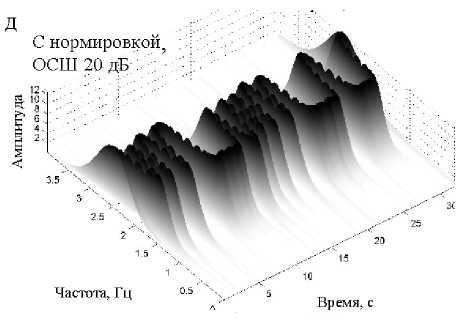
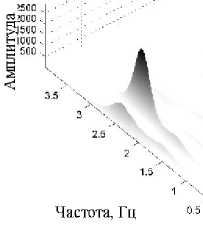
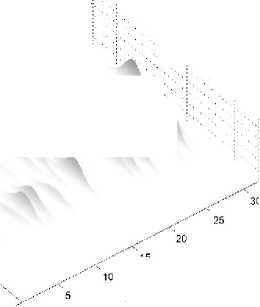
На рис. 5 приведены экспериментальные значения J для основных видов ЧВП. Анализ этих результатов эксперимента показывает, что наибольшей устойчивости к шумам позволяет добиться подход, основанный на вычислении матрицы РЭ с использованием ПФС, двух спектрограмм и НВП Морле. В частности, при ОСШ 10 дБ значение показателя J увеличивается в среднем в 10 раз за счет нормирования временных срезов. На рис. 6 представлены матрицы РЭ тестового сигнала, построенные на основе ПФС [8].

Для практического подтверждения полученных теоретических результатов был проведен эксперимент по измерению нестабильности частоты вращения двигателя на основе оценивания мгновенной частоты контрольного сигнала. На рис. 7 представлены матрицы РЭ контрольного сигнала, вычисленные с использованием нормирования их временных срезов на основе псевдо-ЧВР Вигнера, НВП Морле и ПФС. Качественное сравнение ре- зультатов эксперимента указывает на очевидные преимущества применения показательных (степенных) функций совместно с нормированием временных срезов матриц РЭ (рис. 7, г, д, е).

ЗАКЛЮЧЕНИЕ

Таким образом, для достижения поставленной цели исследования разработан подход к модификации частотно-временных описаний, заключающийся в вычислении показательных (степенных) функций от исходных ЧВП и в последующем нормировании каждого временнóго среза полученных матриц РЭ. Величину основания степени следует выбирать исходя из конкретных условий в зависимости от абсолютных значений и требуемого конечного соотношения элементов матрицы РЭ. При этом ширина окна анализа выбирается исходя из требований к величине временнóго разрешения.

Дальнейшее продолжение исследований авторами видится в исследовании свойств полученных усовершенствованных частотно-временных описаний сигналов на основе показательных (степенных) функций от различных видов ЧВП.

Возможные области их применения не ограничиваются только задачами измерения сигналов датчиков, но также могут найти широкое применение в задачах спектрального образов.

анализа и распознавания

в

,

Без нормировки, осшюдБ: _:

4* '

Время, с

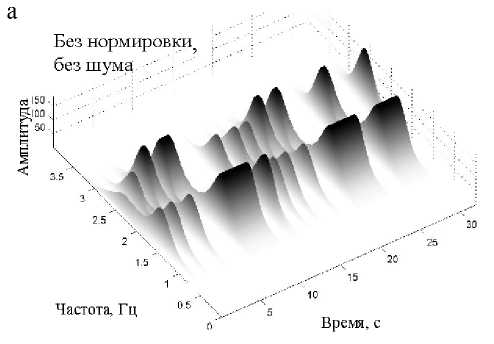
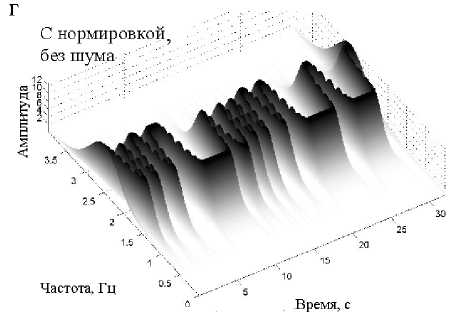
Рис. 6. Матрицы РЭ на основе спектрограммы тестового сигнала при различных ОСШ

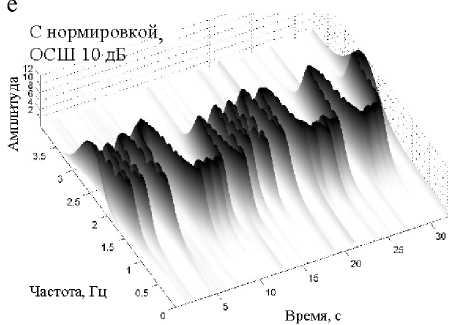
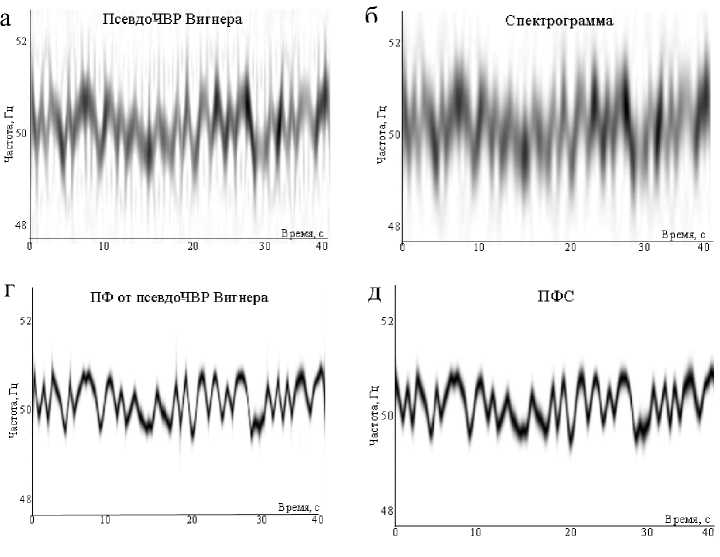
Рис. 7. Вид матриц РЭ для сигнала датчика частоты вращения двигателя: а, б, в — без применения разработанного метода; г, д, е — с применением разработанного метода

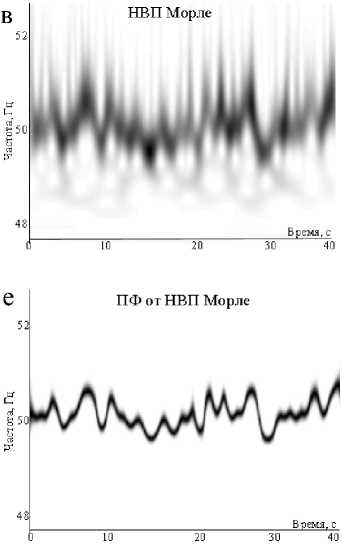
ПРИЛОЖЕНИЕ. Изображения матриц РЭ тестового сигнала для некоторых частотно-временных преобразований

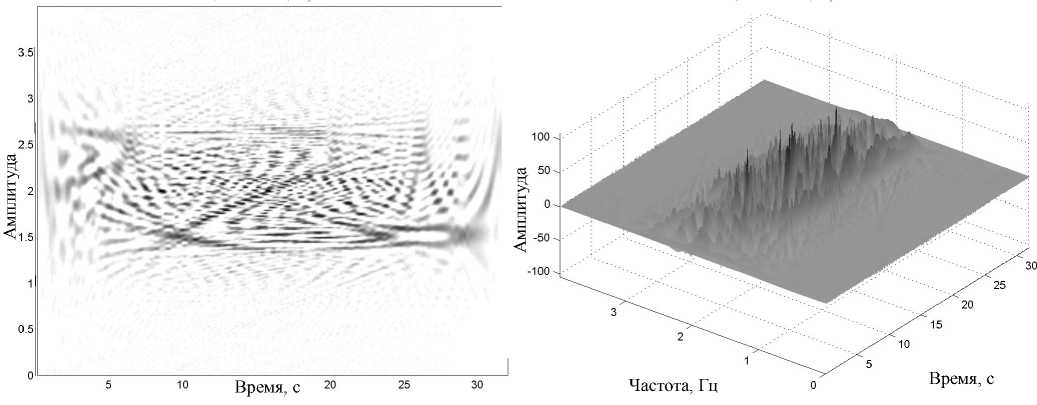
Рис. П1. Матрица РЭ тестового сигнала на основе ЧВР Вигнера

в 2-мерном (а) и 3-мерном (б) представлениях

а

в

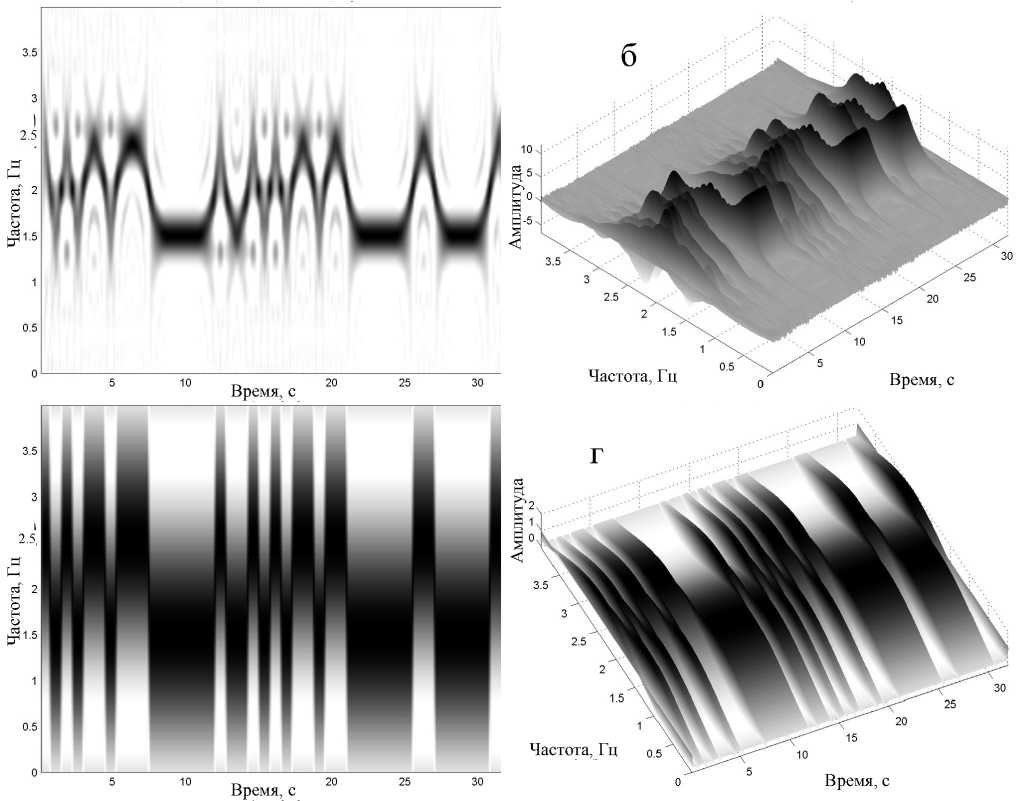
Рис. П2. Матрицы РЭ тестового сигнала, рассчитанные на основе псевдо-ЧВР Вигнера при: n = 21 (а, б); n = 3 (в, г)

а

б

^1=

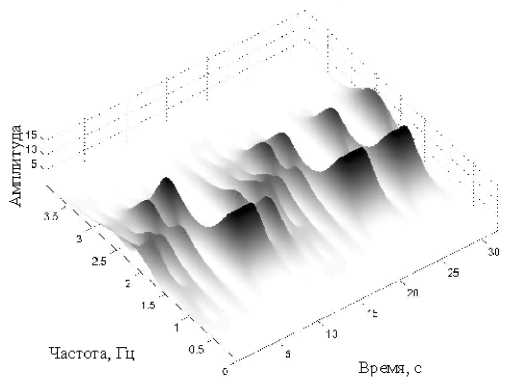
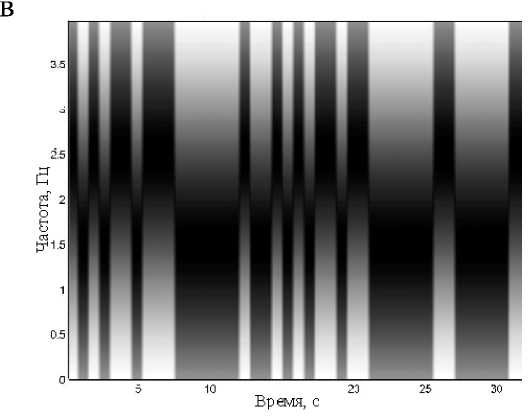
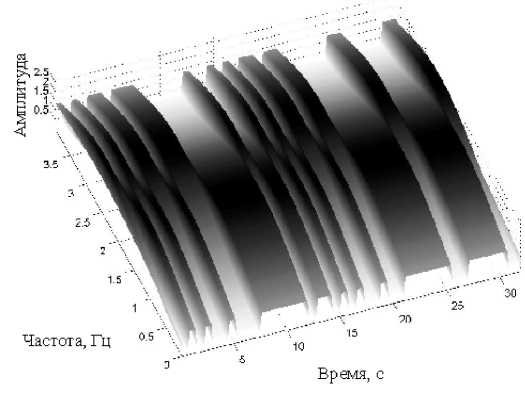
Рис. П3. Матрицы РЭ тестового сигнала, вычисленные на основе КПФ при: n = 21 (а, б); n = 3 (в, г)

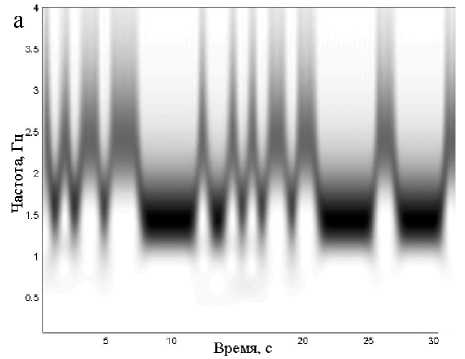
Рис. П4. Матрица РЭ тестового сигнала, построенная на основе НВП Морле, в 2-мерном (а) и 3-мерном (б) представлениях