Модификация GERT-сети для анализа временных характеристик сетевых моделей

Стохастические GERT-сети [1] достаточно хорошо зарекомендовали себя в задачах оценки времени выполнения операции при последовательной обработке данных. Например, их применяют при оценке времени переработки сырья в производстве полупроводников, в производстве электроники и ремонте автономного управления электровоза [2; 3]. GERT-сети также позволяют получить качественно новые результаты при оценке времени выполнения распараллеленной задачи на неспециализированном вычислительном кластере Condor [4; 5].

GERT-сети требуют выполнения условия марковости для вероятностей перехода по дугам (вероятность начала выполнения работы). Кроме того, эти сети не позволяют вводить дополнительные параметры для узлов (состояний) и дуг (работ), что, например, возможно для сетей Петри без условия марковости переходов [6; 7]. Эти требования существенно ограничивают применимость данного метода моделирования. В частности, при помощи стандартных GERT-сетей не может быть разрешена задача оценки вероятности выполнения образовательного процесса в инфор- мационно-образовательном кластере с ограничением на максимальное время реализации процесса.

Результатом работы по устранению описанных выше ограничений GERT-сетей стала математическая модель модифицированной GERT-сети (далее – МGERT-сеть), а также разработка программного модуля, реализующего данную модель.

Обозначения и термины, используемые в данной статье, соответствуют нотации К. Ноймана [1].

Математическая модель МGERT-сети. Рассмотрим граф G ( N , A ), где N – множество узлов сети G , A – множество дуг сети G . Все дуги множества A – ориентированные. Узлы сети пронумерованы.

Примем соглашение: будем считать, что между двумя узлами может быть не более одной дуги в каждом направлении. Тогда каждая дуга a ∈ A может быть однозначно задана парой узлов с номерами i , j , где i – начальный узел; j – конечный узел. Обозначим дугу a как < i , j >.

В нашей сети узлы – это состояния проекта, а дуги – это работы, изменяющие состояние (модель сети – дуга-работа).

Выполнением сети будем называть процесс выполнения случайного эксперимента, а как реализацией сети – итог данного случайного эксперимента.

Пространство случайных выборок W является множеством всех возможных реализаций случайного эксперимента, возникающих при выполнении сети. Выполнение сети происходит путем активации узлов, т. е. возникновения случайных событий «Узел i активирован».

Дуга называется выполненной , если узел, являющийся ее началом, активирован.

Каждый активированный узел обладает набором параметров. Обязательным является только один параметр – вероятность активации узла ip_i . Как правило, определяется еще один параметр – функция распределения времени выполнения сети в момент активации узла F_i .

Каждой дуге сопоставлены функции, изменяющие параметры активированного узла в процессе выполнения работы, соответствующей данной дуге. Таким образом, каждой дуге сопоставлена вычисленная после активации начального узла дуги функция p_ij – условная вероятность выполнения дуги < i , j > при условии активации узла i .

Каждый узел GERT-сети имеет входную и выходную функцию активации (рис. 1).

Входные функции бывают следующих видов:

• –    AND-функция (узел выполняется, если выполнены все дуги, входящие в него);

• –    IOR-функция (узел выполняется, если выполнена любая дуга, входящая в него);

• –    EOR-функция (узел выполняется, если выполнена любая дуга, входящая в него при условии, что в данный момент времени может выполняться только одна дуга).

В свою очередь выходные функции могут быть детерминированными (все дуги, выходящие из узла, выполняются, если этот узел выполнен) и стохастическими (только одна дуга, выходящая из узла, выполняется с заданной вероятностью, если узел выполнен).

Активация узла происходит, если его входная функция выполнена. После выполнения выходной функции активированного узла он становится неактивным.

Активация узла означает, что проект перешел в некоторое состояние и определяет множество возможных дальнейших работ.

Одна или несколько работ (дуг) начинают свое выполнение сразу после активации узла, являющегося их началом.

Определение : будем называть сеть G ( N , A ) МGERT-сетью, если выполняются следующие условия:

• 1)    она представлена ориентированной связанной сетью;

• 2)    сеть обладает, по крайней мере, одним источником и одним стоком;

• 3)    каждый узел из N достижим, по крайней мере, из одного источника и из каждого узла достижим, по крайней мере, один сток;

• 4)    заданы типы входящих и выходящих функций узлов;

• 5)    задано начальное распределение вероятности выполнения источников q _sub, где sub ⊆ R ;

EOR-вход

• 6)    в течение каждого выполнения проекта для каждого стока активируется не более одного источника, из которого этот сток достижим;

• 7)    задан набор параметров, которыми обладает каждый активированный узел (по крайней мере, вероятность активации);

• 8)    для каждой дуги указаны функции преобразования параметров активированного узла;

• 9)    хотя бы один источник активируется в момент времени 0 (если параметр, отвечающий за время, определен).

Условие 6 накладывает ограничение на начальное распределение вероятности выполнения источников и позволяет трансформировать сеть в эквивалентную МGERT-сеть с единственным источником [1]. Таким образом, мы можем рассматривать только МGERT-сети с одним источником (рис. 2).

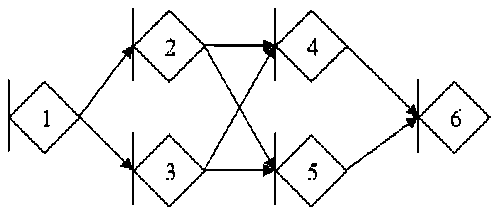
Рис. 2. Пример стохастической МGERT-сети, состоящей из шести элементов

Обозначим Pred(< i , j >, < k , l >) – множество узлов, являющихся ближайшим общим предком для дуг < i , j >, < k , l >. Так, на рис. 2, Pred(<4, 6>, <5, 6>) = {2, 3}.

Аналогично введем Succ(< i , j >, < k , l >) – множество узлов, являющихся ближайшим общим потомком для дуг < i , j >, < k , l >. Так, на рис. 2, Succ(<1, 2>, <1, 3>) = {4, 5}.

Из определения EOR-входной функции узла следует, что для любых двух дуг < j , i >, < k , i >, входящих в узел i c EOR-входом, все узлы из Pred(< j , i >, < k , i >) имеют стохастический выход. В противном случае вероятность того, что более одной дуги будет выполнено одновременно, не равна нулю, что противоречит определению EOR-входной функции.

Из определения IOR- или AND-входной функции узла следует, что для любых двух дуг < j , i >, < k , i >, входящих в узел i c IOR- или AND-входом, все узлы из Pred(< j , i >, < k , i >) имеют детерминированный выход. В противном случае вероятность того, что более одной дуги будет выполнено одновременно, равна нулю, и узел не будет активирован ни разу. В дальнейшем мы будем требовать единственность такого узла. Обозначим его через l и будем говорить, что узел i имеет стохастическое начало в узле l .

Дуга, выходящая из узла i с детерминированным выходом, может не иметь ближайших общих потомков с остальными дугами, выходящими из i . В таком случае

■вход

Стохастический выход

Рис. 1. Обозначения входов и выходов узлов GERT-сети

Детерминированный выход порождаемый ею путь не зависит от всех остальных путей, порожденных другими дугами, выходящими из i, и имеет свой сток.

Так как выполнение сети идет дискретно, т. е. следующий узел активируется только после выполнения условия его входной функции, то каждая конкретная реализация сети представляет собой ориентированный граф истории активаций узлов, который мы будем называть графом реализации . Если в МGERT-сети нет ни одного IOR- или AND-узла, то граф реализации будет цепью. Например, множеством всех графов реализации сети (см. рис. 2) будут четыре цепи (рис. 3).

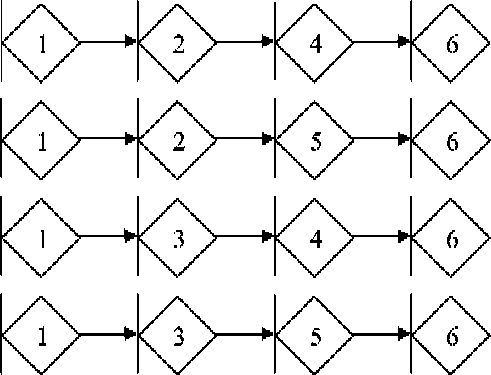
Рис. 3. Множество реализаций сети, изображенной на рис. 2

Множество всех реализаций сети, изображенной на рис. 4, состоит из графа и цепи (рис. 5).

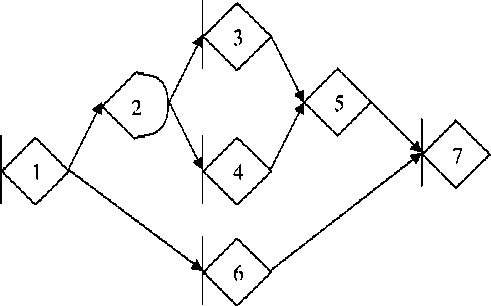
Рис. 4. Пример стохастической МGERT-сети, состоящей из семи элементов

Если сеть содержит циклы, то множество всех ее возможных реализаций бесконечно. Однако многие реализации оказывают несущественное влияние на конечный результат, т. е. вероятность выполнения стока близка к нулю. Поэтому введем дополнительные ограничения на граф реализации:

• а) общие ограничения (обязательные):

• –    реализация сети является допустимой, если в процессе выполнения каждый из активированных узлов сети активируется не более чем max A ≥ 1 раз;

• –    реализация сети является допустимой, если в процессе выполнения каждый из активированных узлов сети активируется с вероятностью больше max P > 0;

• б)    ограничения для каждого из узлов (они могут не использоваться, но если указаны, то отменяют действие общих обязательных ограничений):

  – реализация сети является допустимой, если в процессе выполнения узел i активируется не более чем max A_i ≥ 1 раз;

  – реализация сети является допустимой, если в процессе выполнения узел i активируется с вероятностью больше max P_i > 0.

• в)    ограничения на циклы (обязательные):

• –    если в узел i циклической структуры C входит более одной дуги и хотя бы одна дуга не принадлежит циклу C , то узел i имеет EOR-вход;

• –    если из узла i циклической структуры C выходит более одной дуги и хотя бы одна дуга не принадлежит циклу C , то узел i имеет стохастический выход;

• –    если узел i с IOR- или AND-входом принадлежит циклу, то узел j , являющийся стохастическим началом узла i , принадлежит данному циклу.

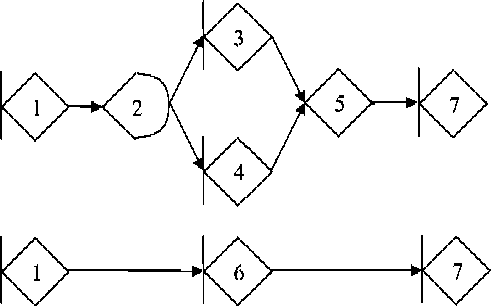
Рис. 5. Множество реализаций сети, изображенной на рис. 4

Таким образом, для любой сети с учетом хотя бы общего ограничения количество реализаций конечно. Заметим, что данные ограничения на циклы не запрещают циклы без входа (они не попадут ни в одну реализацию сети) и без выхода (реализации с такими циклами будут отброшены как недопустимые).

Если выполняются указанные выше условия, то сеть имеет конечное число реализаций, следовательно она может быть вычислена с использованием ЭВМ.

МGERT-сеть с параметром «Функция распределения времени выполнения сети». Введем параметр F ( t ) – функцию распределения времени выполнения сети. Тогда каждой дуге сети должна быть сопоставлена функция F_ij ( t ) условной вероятности распределения времени выполнения работы, соответствующей данной дуге.

Введем следующие обозначения:

• –    p_i – вероятность активации узла i ;

• –    p_ij – функция условной вероятности активации узла j при условии активации узла i , p_ij = 1, если узел i имеет детерминированный выход;

• –    p_{ij н} – вероятность выполнения начала цепи i при условии, что узел, из которого она входит, будет активирован;

• –    p_{ij к} – вероятность выполнения конца цепи i при условии, что узел, в который она входит, будет активирован;

• –    F_i ( t ) – функция распределения времени выполнения узла i в момент его активации;

• –    F_ij ( t ) – функция условной вероятности распределения времени выполнения работы;

• –    F_{ij н}( t ) – функция распределения времени выполнения t_i в начале цепи i при условии, что узел, из которого она входит, будет активирован;

• –    F_{ij к}( t ) – функция распределения времени выполнения t_i на конце цепи i при условии, что узел, в который она входит, будет активирован.

Рассмотрим изменение параметров p и F ( t ):

• –    выполнение дуги < i , j >:

p ij к ⁼ p ij н ^⋅ p ij ^,

+∞

F_{ij к}( t ) = ∫ F_{ij н}( s ) ⋅ F_ij ( t - s ) ds = F_{ij н} ⊕ F_ij .

-∞

Если считать, что случайная величина t > 0, то пределы интегрирования можно заменить на 0 и t соответственно;

• –    формулы расчета для EOR-входа:

p j ⁼ p ij к^, F j ( t ) = F ij к ( t );

• –    формулы расчета для AND-входа:

p j ⁼ p 12к ^⋅ p 34к ^⋅⋅ p (2 N - 1)(2 N )к^/ p i ^, ...

^Fj ^{( t ) =} max ^{( t} 12к^{, t} 34к^{,..., t} (2 N - 1)(2 N )к^{) =}

^{= F} 12к ^{( t ) ⋅ F} 34к ^{( t ) ⋅   ⋅ F} (2 N - 1)(2 N )к^{( t ).}

...

• –    формулы расчета для IOR-входа:

p_j = p_i ⋅ (1 - (1 - p _12к) ⋅ (1 - p _34к) ⋅⋅ (1 - p _{(2 N -1)(2 N )к})),

^Fj ^{( t ) =} m ⁱ n ^{( t} 12к^{, t} 34к ^{,..., t} (2 N - 1)(2 N )к^{) =} = 1 - (1 - F 12к ( t )) ⋅ (1 - F 34 к ( t )) ⋅ ... ⋅ (1 - F (2 N - 1)(2 N )к ( t )).

Формулы, приведенные выше, предназначены для расчета реализации сети по ее графу реализации.

Обработка результатов. Пусть r – элемент множества реализаций со стоком i . Результатом расчета сети будут множества реализаций R_r , сгруппированные по стокам i_r . Для стока в каждой реализации будут рассчитаны следующие характеристики:

• –    вероятность выполнения стока i ∑ p_i ^r ;

• –    вероятность выполнения стока i ко ^r времени t в реализации r p_i^r ∙ F_i^r ( t );

• –    вероятность выполнения стока i ко времени t ∑ p i^r ⋅ F i^r ( t );

• –    математическое ож ^r идание времени выполнения стока i

  E ( t i ) =

  
  

∞

∑ ( p i^r ∫ t ⋅ dF i^r ( t )) r _-∞

∑ p i^r

– математическое ожидание времени выполнения всей сети

E ( t ) =

∞ ∑∑ ( p i^r ∫ t ⋅ dF i^r ( t )) ir -∞

∑ p i^r

• –    дисперсия времени выполнения стока i ∞

∑ ( p i^r ( ∫ t ² ⋅ dF i^r ( t ) - E ( t i ))

D ( t i ) = ^r

-∞

∑ p i^r

r

– дисперсия времени выполнения всей сети

D ( t ) =

∞

∑∑ ( p_i ^r ( ∫ t ² ⋅ dF_i ^r ( t ) - E ( t_i ))) ir -∞

∑ p i^r

Таким образом, представленная в данной статье стохастическая МGERT-сеть имеет более широкую область применения, чем классическая GERT-сеть. Применение дополнительных параметров в узлах сети позволяет использовать ее не только для оценки времени выполнения сети, но и для оценки выполнимости сети в заданных рамках и при заданных отклонениях от проектных параметров.

Следует отметить и недостатки МGERT-сети по сравнению с классическими GERT-сетями:

• –    высокие требования к вычислительным ресурсам на сетях с большим количеством циклов;

• –    необходимость применения численных методов свертки и дифференцирования, что вносит некоторую погрешность в результаты вычислений.

На базе данной математической модели реализована система стохастического моделирования распределенной среды обработки информации и управления [8], которая также может быть использована в составе более крупных программных комплексов.