Модификация метода эмпирических ортогональных функций решения обратной задачи восстановления общего содержания углекислого газа по спутниковым данным

В проблеме потепления климата важен вопрос о влиянии атмосферного углекислого газа. Одни ученые выясняют историческую взаимосвязь изменений климата и колебаний концентрации СО2 в атмосфере по изучению льда. Другие - добиваются количественного объяснения изменений климата от климатообразующих факторов и их вариаций, оценки основных факторов влияния - естественных и антропогенных. Важным является направление моделирования климата, циркуляции атмосферы, переноса вещества. Однако во всех этих направлениях и многих других возникает центральная задача, связанная с верификацией полученных результатов с фактическими значениями содержания углекислого газа в атмосфере Земли [1-3].

Получение такого глобального набора данных с определенной частотой обновления и соответствующей точностью требует применения мониторинговых методов зондирования атмосферы и поверхности Земли из космоса. Многие космические агентства мира создают спутниковые приборы и разрабатывают математические алгоритмы обработки спутниковых данных.

Один из первых приборов, который относится к классу мониторинговых, прибор MODIS (36-канальный спектрорадиометр) [ http://modis.gsfc.nasa.gov ], установленный на спутниках Terra и Aqua, открыл принципиально новый этап глобальных мониторинговых наблюдений «системы Атмосфера+Земля» из космоса. Разработанные тематические продукты на основе данных измерений этим прибором позволяют получать данные об аэрозоле, радиационном балансе, облачности, содержании водяного пара, отражательной способности, температуре подстилающей поверхности и др. в глобальном масштабе на регулярной основе (несколько раз в день).

Однако уникальные пространственно-временные и радиометрические характеристики прибора MODIS не дают возможность получать информацию о газовом составе атмосферы (кроме водяного пара), в частности о содержании углекислого газа и метана в атмосфере. Среди существующих мониторинговых спутниковых приборов, которые позволяют получать информацию о газовом составе атмосферы, можно выделить IASI [ http://smsc.cnes.fr/IASI ] и SCIAMACHY [ http://www.sciamachy.org/ ]. Хотя эти приборы имеют возможность по своим спектральным характеристикам получать информацию об газовом составе атмосферы, они обладают достаточно большим пятном обзора (например, SCIAMACHY – 60 км поперек трассы и 30 км вдоль трассы в надире). Он существенно сужает рамки применения полученных экс-перементальных результатов в научных направлениях, ограничиваясь в большей степени климатическими задачами.

В настоящее время эффективно работает на орбите прибор Фурье-спектрометр среднего разрешения GOSAT [http://global.jaxa.jp/projects/sat/gosat], который позволяет получать опера- тивные данные о содержании в атмосфере климатически важных газов: СО2 и СН4. В данной статье рассматривается методика обработки данных GOSAT с целью получения информации о распределении общего содержания СО2 над территорией. В основе методики лежит метод эмпирических ортогональных функций. Данная статья является продолжением ранее выполненных нами работ по разработке методики для одной пространственно локализованной географической точки [4, 5].

Выбор типа решения обратной задачи

Формально можно выделить две задачи в теории обработки данных оптики атмосферы, это прямая и обратная задачи [6, 7]. Прямая задача подразумевает построение математической модели измерений, в основу которой положены физические представления о процессах взаимодействия излучения с атмосферой и поверхностью Земли. Понятно, что при математической формализации выбранных физических процессов (положенных в основу модели) неизбежно возникают физические приближения, а при численной реализации - математические приближения. Эти приближения в приводят к тому, что полученная физическая модель представляет собой определенное упрощение реальности. Этот факт при решении обратной задачи может вызвать неоднозначность в оценках параметров модели (некорректность). Степень неоднозначности проверяется в сравнении с реальным экспериментом при различных условиях реализации процессов. Также отметим, что число параметров выбранной модели всегда ограничено.

Таким образом, решение прямой задачи – это алгоритм, позволяющий связать измеренные значения с искомыми параметрами физической модели, которую математически можно записать в виде:

y_m(x)=F(x,p), (1)

где y_m(x) - модельный вектор измеряемых величин на приборной сетке х ; F(x,p) - функция от искомых параметров и приборной сетки х .

В нашем случае величины y(x) содержат измерения отраженного от поверхности солнечного излучения в ближней инфракрасной области спектра.

Обратная задача определяет алгоритм, по которому по данным измерений y(x) и физической модели F(x,p) можно восстановить значения неизвестных параметров р . Отметим, что не все параметры р являются восстанавливаемыми ( p_v ), определенная их часть должна быть заранее известна ( p a ). Формально, опираясь на выражение (1), можно записать выражение для решения обратной задачи в виде

Р = F 1 (x,y,p_t), (2)

здесь p_v - набор неизвестных восстанавливаемых параметров; y(x) - вектор измеренных значений; pa - набор известных параметров и Р'О - алгоритм решения обратной задачи, в основе которой лежит функция F() .

Заметим, что в общем случае система (2) может и не иметь решений, что может быть связано с тем, что измеряемый вектор имеет погрешности измерений (y(x)=y_o(x)+£(x), где y o (x) - не-зашумленный (истинный) вектор измерений и e(x) - погрешность измерений, а также тем, что функция F(x,p) является лишь приближением к реальности.

Типично все алгоритмы решения обратных задач основаны на сравнении результатов измерения с моделированием функции (1). Типичная формулировка звучит так: следует найти такой набор параметров прямой задачи р , при котором разница измеренных и рассчитанных значений параметров будет минимальна:

p = min А ( y ( x ), ym (x , p ) ) ,                                                  (3)

)

где p - вектор восстановленных значений параметров (оценка) и А ( y ( x ), ym ( x , p ) ) - функция сравнения измеренного и модельного вектора измерений. Для метода наименьших квадратов и ряда других методов ∆ представляет собой невязку разности этих двух векторов.

Типичный вариант решения уравнения (3), с учетом априорной информации об изменениях параметров p , представлен следующим выражением:

p = p o + ( J T S - J + S - ) J T S ^- ( y - y_m ( p o )),                              (4)

) здесь p – вектор неизвестных параметров; ро – вектор начального приближения параметров; y - вектор измерений; ym - модельный вектор измерений, рассчитанный для начального значе- дy ния параметров; J = —m

5 p

• - матрица Якоби, рассчитанная для приближения р о ; S_E - ковариа- p o

ционная матрица шума измерений; S_p – ковариационная матрица априорной информации об искомых параметрах.

Анализ типично применяемого подхода решения обратной задачи (4) приводит к выво-

)

ду [4, 5], что существует зависимость оценки p : 1) от типа выбранной физической модели и приближений; 2) от объема и качества априорной информации; 3) от размерности вектора не ₎

известных параметров p и измеренных значений; 4) от качества определения характеристик погрешности измерений.

Указанные выше и некоторые другие особенности решения, с одной стороны, позволяют получать соответствующего качества решения (оценки), однако эти оценки весьма затратны по времени при больших размерностях вектора измерений; существенно зависят от величины погрешности, могут при решении получать физически неверные результаты (обнуления, отрицательные значения и др.); требуют правильного и тщательного выбора физической модели и приближений.

Учитывая эти моменты, мы для решения обратной задачи применяем метод эмпирических ортогональных функций [8-11], который относится к классу непараметрических алгоритмов. Последнее свойство указывает на факт того, что не существует явной модели, связывающей измерения и искомую оценку неизвестных параметров.

Описание методики ЭОФ и ее модификация

Основная методика получения эмпирических ортогональных функций (ЭОФ) является классической процедурой и состоит из нескольких вычислительных этапов:

Этап 1. Расчет ковариационной матрицы K=RRT, R=(Y-).

Этап 2. Расчет собственных векторов E и собственных значений Λ матрицы K из решения характеристического уравнения (K-ΛI)=0.

Этап 3. Вычисление эмпирических ортогональных функций F=ETR.

Этап 4. Вычисление коэффициентов линейной регрессии P=

+cF.

На первом этапе формируется матрица вычислений Y=Y(i,j), где i=1,N – число длин волн измеренных значений и j=1,M – число измерений. Ковариационная матрица – квадратная с размером [NxN].

Модификация метода ЭОФ заключается в модификации матрицы измерений и включении в нее априорной информации. Априорной информацией является зенитный угол Солнца, рельеф, оптические толщи аэрозоля и водяного пара. Для каждого измерения значения априорной информации – различны, что не влияет на вычислительные свойства матрицы в целом, но повышает качество решения.

Результаты применения методики

Для решения климатических задач в 2009 г. японским космическим агентством был запущен спутник IBUKI с Фурье-спектрометром среднего разрешения GOSAT на борту. Каждый сигнал GOSAT представляет собой набор спектральных точек, получаемых Фурье-спектрометром в четырех каналах (около 20 тысяч точек в ближнем ИК (с центрами 0.7, 1.6, 2.1 мкм) и ИК (12 мкм) участках спектра). Три первых канала принимают отраженное солнечное излучение от поверхности, а четвертый (ИК-канал) получает уходящее тепловое излучение системы атмосферы и Земли. Спутник пролетает каждые три дня над одной и той же точкой на поверхности. Нами выбирались данные второго канала (около 8000 точек), из которых для обработки взяты данные (1800 точек), в которых расположены полосы поглощения углекислого газа и метана. Далее все выбранные спектральные точки сигналов за весь временной промежуток времени проходили оценку на вариабельность. Для дальнейшей работы оставляли наиболее изменчивые по величине спектральные точки сигнала, которых оказалось всего 280.

Нами проделана работа по развитию предлагаемой методики эмпирических ортогональных функций при работе не только для одной пространственной точки, но и для большой территории. Для этих целей нами была выбрана территория США, на которой существует сеть станций TCCON, а именно Lamont, Four Coners и Park Falls [ http://www.tccon.caltech.edu ] (рис.

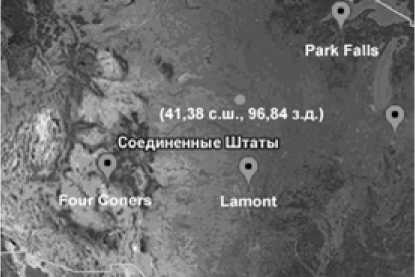
Рис. 1. Положение станций TCCON и промежуточных точек оценки содержания СО2

Fig. 1. Geographical location of TCCON stations and intermediate points of total CO2 content estimation

• 1). Координаты станций: Lamont (36.604 с.ш., 97.486 з.д., Park Falls (45.945 с.ш., 90.273 з.д.) и Four Corners (36.797 с.ш, 108.48 з.д.). Данные измерений общего содержания СО 2 на этих трех станциях являются базовыми для обучения метода ЭОФ и дальнейшего восстановления общего содержания СО 2 на всей территории США.

Для обучения нами были получены данные измерений GOSAT; например, для станции Lamont было получено 5785 сигналов за все время измерений (2009-2014 гг.), в каждом из которых было 280 спектральных точек.

Был выполнен процесс обучения для всех трех станций одновременно за все годы получения сигналов. Для дальнейшего сравнения качества работы нашего алгоритма для всей территории США приведем результаты сравнения для одной реперной точки – станции Lamont и произвольной другой точки территории США только за 2012 г. После обучения и решения обратной задачи стандартным подходом ЭОФ для тестовой выборки результаты восстановленного общего содержания СО2 сравнивались со значениями для станции Lamont, которые показаны на рис. 2 и модифицированным методом на рис. 4. Такая же процедура выполнялась для метода ЭОФ для произвольных точек территории США, что показано на рис. 4-8. Модифицированным считается метод, когда матрица измерений дополнялась априорными значениями (зенитный угол Солнца, при котором получен сигнал, общее содержание аэрозольной составляющей атмосферы и водяного пара на основе данных GOSAT уровня L2).

Сравнение результатов работы стандартного и модифицированного алгоритмов показывает, что точность восстановления общего содержания СО 2 предлагаемым модифицирован-

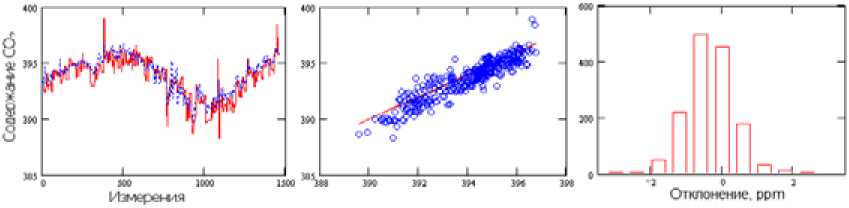
Рис. 2. Рассчитанное общее содержание СО 2 для станции Lamont стандартным методом

Fig. 2. Calculated total CO 2 content for Lamont station by standard method

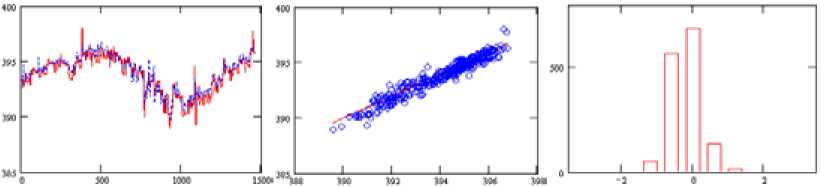
Рис. 3. Рассчитанное общее содержание СО 2 для точки с для станции Lamont модифицированным методом

Fig. 3. Calculated total CO2 content for point of the Lamont station by a modified method

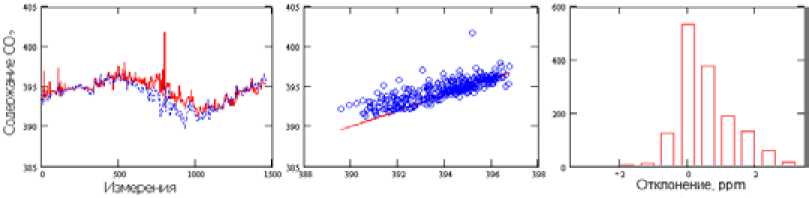
Рис. 4. Рассчитанное общее содержание СО 2 для точки с координатами (41.38 с.ш., 96.84 з.д.) стандартным методом

Fig. 4. Calculated total CO2 content for a point with coordinates (41.38 N, 96.84 W) by the standard method

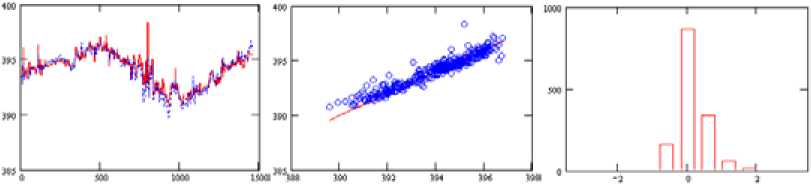
Рис. 5. Рассчитанное общее содержание СО2 для точки с координатами (41.38 с.ш., 96.84 з.д.) модифицированным методом

Fig. 5. Calculated total CO2 content for a point with coordinates (41.38 N, 96.84 W) by a modified method

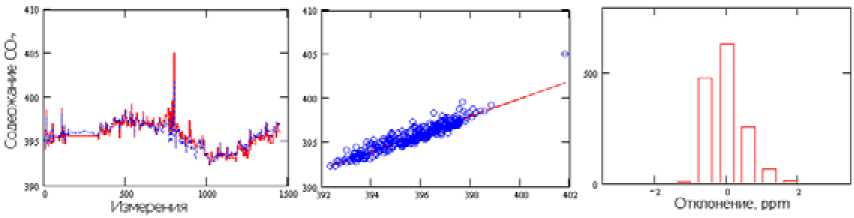
Рис. 6. Рассчитанное общее содержание СО2 для точки с координатами (38.24 с.ш., 105.48 з.д., рядом со станцией Four Corners) модифицированным методом

Fig. 6. Calculated total CO2 content for a point with coordinates (38.24 N, 105.48 W, near the Four Corners station) by a modified method ным методом выше. Предлагаемый вариант обучения на трех точках, находящихся в разных частях исследуемой территории, позволяет с приемлемой точностью восстанавливать общее содержание CO2 не только в выбранных точках, но и по всей территории. Графики гистограмм отклонений (крайний правый рисунок) показывают, что погрешность не превосходит 1 % (все результаты менее 2 ppm). Однако следует отметить, что при восстановлении возникает некоторое незначительное смещение (средний график рисунков), которое еще предстоит оценить и определить причину его появления в следующих работах. Можно лишь предположить, что на – 83 –

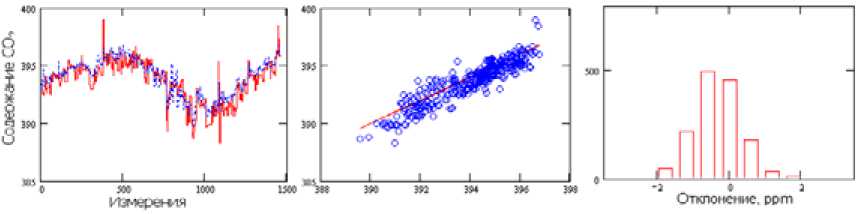
Рис. 7. Рассчитанное общее содержание СО 2 для точки с координатами (42.37 с.ш., 98.87 з.д.) модифицированным методом

Fig. 7. Calculated total CO2 content for a point with coordinates (42.37 N, 98.87 W) by a modified method

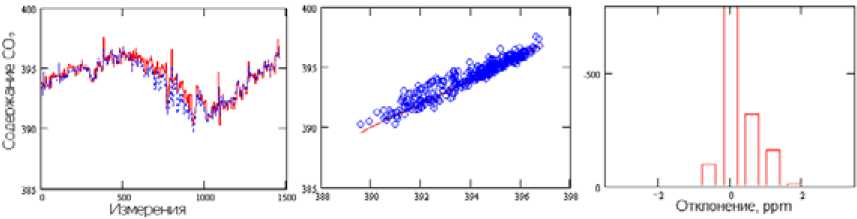
Рис. 8. Рассчитанное общее содержание СО 2 для точки с координатами (46.5 с.ш., 92.26 з.д., рядом со станцией Park Falls) модифицированным методом

Fig. 8. Calculated total CO2 content for a point with coordinates (46.5 N, 92.26 W, next to the Park Falls station) by a modified method восстановлении сказывается положение реперной точки, которое определяет тип воздушных масс, а значит, и структуру пространственно-временного поведения общего содержания СО2.

Заключение

В статье рассмотрен метод эмпирических ортогональных функций и его модификация при решении обратной задачи восстановления общего содержания углекислого газа по спутниковым данным измерений отраженного солнечного излучения Фурье-спектрометром среднего разрешения GOSAT. Для определения устойчивости и работоспособности предлагаемого метода была выбрана территория США, на которой присутствуют подспутниковые (реперные) станции измерений общего содержания СО 2 похожим на спутниковый Фурье-спектрометром. Результаты обработки реальных спутниковых данных показали, что метод применим не только для одной точки, но и для территории с несколькими территориально разнесенными реперными точками. Одним из возможных приложений результатов данной работы является их экологическая направленность [12].